3.

Giochi di magia matematica

La matematica è un gioco

e comunica totale magia.

(Anagramma di Mister Aster)

La Matematica è ritenuta una materia arida e noiosa solo da chi la considera unicamente come la disciplina che insegna a fare i conti. In realtà, nel processo di risoluzione di un problema matematico, lo svolgimento dei calcoli costituisce solo il momento terminale (oggettivamente, monotono e ripetitivo); la fase più importante e assai più stimolante è, invece, quella relativa alla ricerca del procedimento da seguire.

Il ricorso a delle proposte ludiche consente di affrontare in maniera piacevole la soluzione di problemi di varia complessità e risulta, quindi, molto più coinvolgente della proposizione di quell’arido e intricato guazzabuglio di passaggi algebrici che, tradizionalmente, deprime e scoraggia la maggioranza degli studenti di ogni ordine e grado.

Martin Gardner, in particolare, ha dichiarato: «Mi è sempre sembrato che il modo migliore per rendere interessante la Matematica agli studenti e ai profani sia quello di accostarvisi con uno spirito giocoso. Sta di fatto che il miglior modo di tener sveglio uno studente è presentargli giochi matematici interessanti, enigmi, trucchi, battute, paradossi, modelli, limerick o una qualsiasi delle centinaia di cose che gli insegnanti ottusi tendono a evitare perché paiono loro frivole [...]. Nessuno dice che un insegnante non debba fare altro che divertire i propri studenti. Deve esserci un interscambio tra serietà e divertimento: quest’ultimo tiene desto l’interesse, mentre la serietà giustifica il divertimento».

In particolare, la caratteristica della Matematica, di riuscire a prevedere il risultato finale di una serie di operazioni, consente di confezionare dei divertenti giochi di prestigio.

Oltre a rappresentare una stimolante forma di divertimento creativo, i giochi di magia matematica possono costituire un valido strumento di motivazione allo studio della Matematica. In genere, infatti, l’innata tendenza umana a svelare l’arcano spinge ad applicarsi con molto impegno nella ricerca di una spiegazione razionale. In una simile operazione, tra l’altro, si è portati naturalmente a collegare i concetti teorici con l’esperienza reale, dovendo necessariamente interpretare in chiave matematica ogni singola azione compiuta.

Uno dei più semplici di questi giochi, proponibile anche a un pubblico piuttosto numeroso, può essere eseguito con queste modalità.

1. Fornite ai vostri spettatori le seguenti istruzioni collettive (specificando che ognuno di loro dovrà eseguirle in maniera indipendente, senza consultarsi con gli altri):

a) pensate a un numero intero qualsiasi (ad esempio: 7);

b) moltiplicate per 2 il numero pensato (2×7 = 14);

c) aggiungete 10 al prodotto ottenuto (14+10 = 24);

d) dividete per 2 il totale ottenuto (24:2 = 12);

e) dal risultato così ottenuto, sottraete il numero a cui avevate pensato all’inizio (12−7 = 5).

2. A questo punto, chiedete che, a un vostro via, ogni spettatore dica ad alta voce, insieme agli altri, il risultato che ha ottenuto.

3. Date il via e, con un certo stupore, tutti gli spettatori diranno in coro: «5»! (lo stesso risultato ottenuto nel nostro esempio...)

Per poter capire come mai questo gioco funziona sempre, basta ricorrere a una semplice applicazione algebrica.

A tale scopo, indichiamo con N il numero scelto da un generico spettatore. In base alle serie di operazioni richieste, il risultato finale R sarà dato dalla seguente espressione:

R = (2N+10)/2 − N

Se svolgiamo i calcoli, otteniamo:

R = 2N/2+10/2 −N;

R = N+5−N;

R = 5 (dato che N−N = 0).

Per questo motivo, indipendentemente dal numero N pensato, il risultato sarà sempre uguale a 5.

Un gioco formalmente analogo al precedente, ma basato su un principio diverso, può essere eseguito con queste modalità.

1. Fornite ai vostri spettatori le seguenti istruzioni collettive (specificando che ognuno di loro dovrà eseguirle in maniera indipendente, senza consultarsi con gli altri):

a) scegliete un numero intero di due cifre (ad esempio: 85);

b) sottraete da questo numero i valori delle sue due cifre (85–8–5 = 72);

c) eseguite la somma delle cifre del numero ottenuto (7+2 = 9).

2. A questo punto, chiedete che, a un vostro via, ogni spettatore dica ad alta voce, insieme agli altri, il risultato che ha ottenuto.

3. Date il via e, con un certo stupore, tutti gli spettatori diranno in coro: «9»! (lo stesso risultato ottenuto nel nostro esempio...)

Il motivo che genera questo sorprendente effetto può essere compreso tenendo presente che un qualsiasi numero di due cifre, composto da X decine e Y unità, può essere scritto come:

10X+Y; eseguendo le due operazioni richieste, si ottiene, quindi:

10X+Y–(X+Y) = 9X.

Il risultato, di conseguenza, è un multiplo di 9, indipendentemente dal numero di partenza. Inoltre, per un noto criterio di divisibilità, la somma delle cifre di un multiplo di 9 è sempre uguale a 9 o a un multiplo di 9, di minor valore.

Quest’ultima regola, che si impara acriticamente a scuola, può essere compresa a fondo, mediante le seguenti considerazioni.

• La moltiplicazione è un’addizione ripetuta; quindi, ogni multiplo di 9 può essere ottenuto addizionando un 9 al multiplo precedente.

• Se si addiziona 9 a un determinato multiplo di 9, che possiamo chiamare M, si possono avere solo due possibilità:

– l’ultima cifra di M è diversa da zero; in questo caso, la somma delle cifre del numero risultante è uguale a quella precedente; infatti, siccome: 9 = 10–1, aggiungere 9 a un determinato numero equivale a incrementare di 1 la quantità delle sue decine e a decrementare di 1 quella delle sue unità, mantenendo immutata la quantità globale (ad esempio, se M = 27, si ha 2+7 = 9; e siccome: M+9 = 27+9 = 27+10–1 = 36, si ha ancora: 3+6 = 9);

– l’ultima cifra di M è uguale a zero; in questo caso, la somma delle cifre del numero risultante è uguale a quella di M, aumentata di 9 (ad esempio, se M = 90, si ha: 9+0 = 9; e, siccome: M+9 = 90+9 = 99, si ha: 9+9 = 18).

• In definitiva, siccome il primo multiplo di 9 è proprio 9 (in quanto: 9×1 = 9), la somma delle cifre di un qualsiasi altro multiplo di 9 deve necessariamente essere uguale a 9 o a un multiplo di 9, di minor valore.

Su questo stesso principio si basa un’altra sorprendente curiosità, che può essere così evidenziata.

• Aprite le mani di fronte a voi e assegnate mentalmente alle dita i valori da 1 a 10.

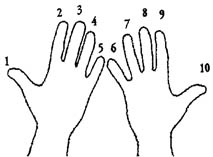
• Immaginate, ora, di non ricordare più la ‘tabellina del 9’; ovvero, l’insieme dei risultati delle moltiplicazioni di 9 per i numeri compresi tra l a 10.

• Per ricavare uno qualsiasi di questi valori non dovete far altro che piegare il dito corrispondente al numero (compreso tra 1 e 10) per cui volete moltiplicare 9: il risultato sarà miracolosamente scritto sulle vostre mani!... Infatti, la quantità di dita che si verranno a trovare a sinistra del dito piegato rappresenteranno le decine del risultato desiderato e quelle a destra le rispettive unità.

• Ad esempio, se volete moltiplicare il 9 per 4, dovete piegare il 4º dito.

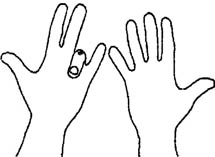
A sinistra del dito piegato ci sono 3 dita, mentre a destra ce ne sono 6; quindi, 3 decine e 6 unità (ovvero: 36). In definitiva, 9×4 = 36.

• Provate a calcolare 9×8, con lo stesso procedimento. Questa volta, dovete piegare l’8º dito.

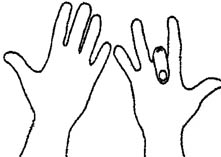
Siccome ottenete 7 dita a sinistra e 2 a destra, potete affermare che: 9×8 = 72.

In base ai ragionamenti analizzati in precedenza, questo metodo funziona perché, procedendo da sinistra verso destra, ogni volta che si piega un nuovo dito si elimina un’unità e si aggiunge una decina, rispetto alla situazione precedente. Il seguente schema evidenzia tale meccanismo, riportando la successione di tutti i casi ottenibili.

dita a sinistra	0	1	2	3	4	5	6	7	8	9
dita a destra	9	8	7	6	5	4	3	2	1	0

I giochi precedenti non richiedono lo svolgimento di alcuna operazione aritmetica da parte di chi li propone. È vero che un buon matematico non deve necessariamente essere anche un esperto di calcolo mentale; all’occorrenza, infatti, può sempre utilizzare una calcolatrice elettronica. È anche vero, però, che la capacità di saper effettuare a mente almeno i calcoli più elementari può risultare molto utile in diverse circostanze (ad esempio, quando non si dispone di una calcolatrice elettronica...).

In tale ottica, è consigliabile esercitarsi anche con giochi che richiedono l’effettuazione di alcuni calcoli mentali. Uno dei più sorprendenti di questi può essere eseguito con le seguenti modalità.

1. Porgete un comune mazzo di 40 carte a uno spettatore e chiedetegli di toglierne una a sua scelta, senza farvela vedere.

2. Fatevi riconsegnare il mazzo e analizzate velocemente il suo contenuto solo un paio di volte.

3. Al termine di questa operazione, comunicate con sicurezza quale carta è stata tolta dal mazzo.

Gli accorgimenti da seguire per poter ottenere un simile sorprendente risultato sono i seguenti.

• Attribuite a ciascuna carta il valore di presa che tradizionalmente essa ha nel gioco della Scopa (asso = 1, due = 2, tre = 3, ecc.), a eccezione del re, al quale dovete assegnare il valore 0.

• Mentre sfogliate per la prima volta il mazzo, effettuate mentalmente la somma progressiva dei valori delle carte che, di volta in volta, vi capitano sotto gli occhi, memorizzando solo la cifra delle unità di ogni risultato parziale ottenuto. Ad esempio, eseguendo: 7+8 = 15, dovete tenere a mente soltanto: 5.

• Al termine di queste operazioni, ottenete un risultato compreso tra 0 e 9; sottraendo questo numero da 10, ricavate il valore della carta messa da parte.

• Quando sfogliate il mazzo per la seconda volta, osservate i semi con cui compare il valore che avete prima individuato; in questo modo, per esclusione, potrete facilmente individuare quello mancante. Una tale manovra può servirvi anche per controllare l’esattezza dei calcoli compiuti in precedenza; infatti, se vi accorgete che nel mazzo sono presenti tutte le quattro carte del valore da voi determinato (e non solo tre), vuol dire che avete sbagliato a fare le somme...

Per riuscire a interpretare il trucco su cui si basa questo gioco, basta considerare che la somma di tutti valori attribuibili alle 40 carte di un mazzo completo è uguale a 180. Di conseguenza, se non venisse tolta alcuna carta, l’operazione descritta in precedenza darebbe come risultato 0 (scartando, una alla volta, tutte le decine di 180). Per questo motivo, quando viene tolta una carta, il suo valore coincide con il numero che bisogna aggiungere al risultato ottenuto, per ottenere 10 (ovvero 0, scartando la cifra delle decine).