Chapter 15
Elicitation
15.1 Methods and issues
The elicitation of imprecise probabilities is a relatively unexplored topic, and so some parts of this review will draw from work on precise probability judgements. Most methods of eliciting imprecise probabilities fall into three groups: Direct numerical estimates, numerical translations of verbal probability expressions (e.g., ‘somewhat likely’), and evaluations of candidate intervals or bounds. We shall begin by surveying these in turn, elaborating the issues and methods in evaluating judged imprecise probabilities. The section thereafter examines methods for evaluating judged probabilities that can be adapted and applied to imprecise probability judgements. The third section discusses factors that influence probability judgements and ways in which elicitation methods may be matched with the purposes intended to be served by elicitation. The final section provides a guide to further reading on this topic.
Numerical elicitation methods range from simply asking for numerical estimates to inferring such estimates from other indicators. Until recently relatively little work had been done comparing these methods with one another or with other alternatives. The most obvious direct numerical estimation task is to ask for a lower and upper bound on the probability of an event. This is rather problematic because no criterion is given for the bounds. The most commonly employed criterion is a confidence level (e.g., within what bounds are you 95% confident that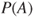 
lies?). There is a sizeable empirical literature on how people construct predictive ‘confidence intervals’ of this sort, although it is not based on estimations of probabilities ([436, 550]). We shall review this literature in the third subsection.
A second criterion relies on the interpretation of lower and upper probabilities as buying and selling prices or bid-ask spreads. The judge is asked to nominate a maximum buying price,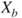 
, to purchase a gamble paying 1 unit if event 
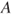occurs and a minimum selling price, 
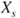, for the same gamble. The judge also is asked for a maximum buying and a minimum selling price, 
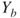and 
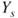, for a gamble paying 1 unit if the complement 
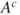occurs. Assuming 
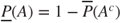, we may infer
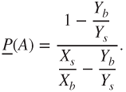
A third possible criterion involves the application of a ‘scoring rule’, such that the estimator is rewarded in accordance with how much weight she gives the event that occurs relative to others. The scoring rule can be used as a motivating device. For precise probabilities assigned to a finite exhaustive collection of events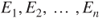 
, the score 
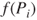is the payoff if 
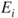occurs. Popular examples include the quadratic rule 
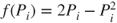and the logarithmic rule 
. A simple adaptation to lower and upper probabilities would be to use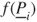 
.
A fourth approach, related to the buying-selling price interpretation, is inferring utilities from imprecise probability assignments and vice-versa [603]. We begin with the (non)occurrence of event 
consideration and an ordered collection of options 
, 
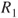, and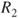 
, one of which is to be selected depending on the probability 
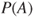and the decision-maker's utilities regarding the outcomes produced by the 
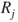given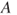 
versus outcomes given 
.
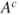A straightforward argument shows that if the odds of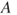 
, 
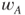, exceed the threshold 
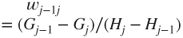then the decision-maker should prefer act 
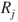over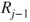 
. The threshold odds 
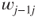therefore are determined by the ratio of utility differences. Thus, elicitation of the 
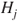and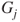 
yield a lower odds 
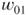and an upper odds 
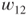. Of course the converse also can be applied. Thus, given a judge's lower and upper probabilities, the resulting utilities of being right or wrong about the occurrence of the event given the decision to be taken can be fed back to the judge to ascertain whether they accord with her preferences.
| State: |  |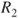
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
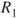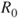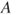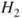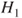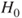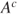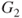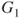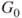Verbal probability expressions may be regarded as imprecise probabilities. If such expressions have an agreed-upon numerical translation then the elicitation task reduces to the judge simply choosing from a set of these expressions. There is a long history of attempts to translate verbal probability expressions into numerical form and debates over whether the results are sufficiently useful.
Early researchers asked people to nominate precise probabilities corresponding to verbal phrases. On the positive side, these investigations yielded reports of reasonably high intra-subjective reliability (e.g., [437, 73, 89] [681]) and reliable aggregate means ([591, 592, 528]). Some of these findings highlighted relevant differences between meanings or usages in natural vs. formal language. For instance, negation was found to be asymmetric in its effects, so that ‘unlikely’ is not subjectively equivalent to 1 - ‘likely’.
However, the same research also revealed considerable inter-subjective variability and overlap among phrases ([614, 437, 73] [77]). [89] argued that verbal probability phrases may lead to ordinal confusion in usual communication, and [90] provided evidence that people vary widely in the probability phrases they regularly use.
One reasonable interpretation of these findings is that they are symptomatic of fuzziness instead of unreliability. Wallsten et al. [682] established an experimental paradigm in which subjects constructed fuzzy membership functions over the unit interval to translate probabilistic quantifiers into numerical terms (see the material on interval evaluation below). Kent [392] anticipated this idea by proposing probability intervals as translations of a set of verbal expressions he hoped would be adopted by American intelligence operatives. However, although the British intelligence community eventually adopted this approach, the American intelligence community has not [393]. Translations of verbal probabilities into numerical imprecise probabilities seem likely to succeed only in small communities of experts who can agree on nomenclature and, of course, the translation.
The fuzzy membership approach generalizes the staircase method, but brings with it an additional issue, namely the meaning of a ‘degree of membership’ (see [607], § 3). When restricted to judgements of one fuzzy set, this does not pose any more difficulties for measurement than many other self-reported numerical estimates. Nevertheless, degree of membership lacks an agreed-upon behavioural definition of the kind exemplified in the betting interpretation of probabilities.
A natural generalization of interval evaluation that incorporates probability judgements is to present an interval to respondents and ask them for their subjective probability that the interval contains the correct answer. This approach has become popular in recent years because of evidence that it yields reasonably well-calibrated estimates, and there is an empirical literature comparing this method with direct interval elicitation (e.g., [706]).
15.2 Evaluating imprecise probability judgements
Standardized methods for evaluating imprecise probability judgements have yet to be developed. This subsection describes methods for evaluating judged probabilities that can be adapted and applied to imprecise probability judgements. We address four issues:
- Factors affecting responses;
- Calibration;
- Response style heterogeneity; and
- Coherence.
Factors affecting the response given may include characteristics of the respondent, the task, and the context or setting in which the elicitation took place. Several well-known influences on probability judgments are reviewed in the next subsection. An appropriate GLM for modelling such influences assumes that judged probabilities follow a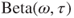 
distribution. We reparameterize these component distributions in terms of a location (mean), 
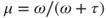and precision parameter 
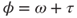(for further details see [607]). The GLM uses a logit link for the location submodel and a log link for the dispersion submodel. The location submodel is
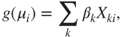
For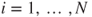 
and 
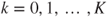where the link function is 
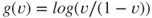, the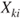 
are predictors and the 
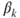are coefficients. The dispersion submodel is
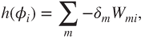
for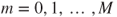 
where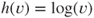 
.
Generalizing this to judged lower and upper probabilities entails modelling both simultaneously via a beta GLM with a random intercept in the location submodel to model the respondent effect. A ‘null’ model with no predictors is
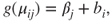
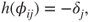
for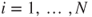 
and 
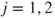, where 
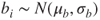. This model is quite similar to a number commonly employed in the behavioural sciences, including unidimensional item-response theory models or those for repeated measures experiments (for a detailed treatment of this kind of model, see [655]).
Calibration refers to the extent to which judged probabilities track true probabilities of predicted events, versus systematically over-estimating them (over-confidence) or under-estimating them (under-confidence, see next subsection). For precise probabilities, beta GLMs can be used in a straightforward way to assess calibration, i.e., by testing whether the coefficient for a regression model with the logit of the true probability as predictor differs from 1. For imprecise probabilities, standard methods have yet to be developed. An obvious approach suited to lower and upper probabilities is comparing the number of times the true probability lies above or below the lower-upper probability assignments.
A somewhat more sophisticated approach is to use the random-effects model in Equations (15.7) and (15.8) with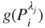 
substituted for the 
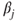term in equation (15.7), where 
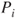denotes the true probability for the 
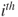case. Let 
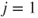correspond to the lower probability assignments and 
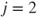correspond to the upper probabilities. If 
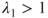and 
then the lower and upper probabilities appear to be well-calibrated. On the other hand,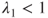 
indicates over-estimation and 
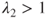indicates under-estimation.
Response style heterogeneity refers to the existence of subpopulations whose probability assignments are distinguishable from one another. The study of partition dependence in [606] used a beta-mixture GLM to identify two subgroups, one anchoring their probabilities around 1/2 and the other anchoring around 1/7. Smithson, Merkle and Verkuilen [605] describe these mixture models and present examples of their application. One of these involves modelling adherence to and deviations from coherence in lower-upper probability assignments, and so we reproduce that example here.
15.3 Factors affecting elicitation
Elicitations of numerical estimates, particularly those involving probability judgements, are notorious for their vulnerability to extraneous factors as well as human heuristics and biases. We shall limit this review to the three influences on subjective interval estimates and probability judgements that have generated the greatest concerns about their validity: Over- and under-weighting, overconfidence, and partition dependence.
There is a large body of empirical and theoretical work on subjective probability weighting. A widely accepted account may be summarized by saying that people over-weight small and under-weight large probabilities [386]. Note that this claim does not mean that people are under- or over-estimating the probabilities, but instead treating them in a distorted fashion when making decisions based on them. Rank-dependent expected utility theory (e.g., [522]) reconfigures the notion of a probability weighting function by applying it to a cumulative distribution whose ordering is determined by outcome preferences. Cumulative prospect theory [637] posits separate weighting functions for gains and losses.
Two psychological influences have been offered to explain the properties of probability weighting functions. The hypothesis proposed in [637] is ‘diminishing sensitivity’ to changes that occur further away from the reference-points of 0 and 1. This would account for the inverse-S shape, or curvature, of the weighting function typically found in empirical studies (e.g., [93]). [317] add the notion of ‘attractiveness’ of a gamble to account for the elevation of the weighting curve. The magnitude of consequences affects both the location of the inflection-point of the curve and its elevation, in the expected ways. Large gains tend to move the inflection point to the left and large losses move it to the right (e.g., [265]).
Diminishing sensitivity has an implication for judgements and decisions based on imprecise probabilities that goes beyond treating their location in a distorted fashion. [317] presented respondents with the following question:
You have two lotteries to win $250. One offers a 5% chance to win the prize and the other offers a 30% chance to win the prize.
A: You can improve the chances of winning the first lottery from 5 to 10%.
B: You can improve the chances of winning the second lottery from 30 to 35%.
Which of these two improvements, or increases, seems like a more significant change?
The majority of respondents (75%) viewed option A as the more significant improvement. In this way they demonstrated that a change from .05 to .10 is seen as more significant than a change from .30 to .35, but a change from .65 to .70 is viewed as less significant than a change from .90 to .95. An implication is that for decisional purposes people might treat a probability interval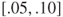 
as less precise than 
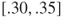, and so on.
We now turn to overconfidence. A large empirical literature on subjective confidence-interval estimation tasks suggests that people tend to be overconfident in the sense that they construct intervals that are too narrow for their confidence criteria (e.g., [12, 396]). If directly elicited subjective probability intervals are psychologically similar to other kinds of confidence-intervals, then overconfidence will occur there too. Nor is this confined to laypeople or novices. In a study of experts' judgemental estimates ([550]), in which business managers estimated 90% confidence-intervals for uncertain quantities in their areas of expertise (e.g. petroleum, banking, etc), the hit rates obtained in various samples of managers ranged from 38% to 58%. These are performance levels similar to those typically found in studies of lay people.
Yaniv and Foster [712, 713] suggest that the precision of subjective interval estimates is a product of two competing objectives: accuracy and informativeness. The patterns of preference ranking for judgements supported a simple trade-off model between precision (width) of interval estimates and absolute error which they characterized by the error-to-precision ratio. Both papers present arguments and evidence that people tend to prefer narrow but inaccurate interval estimates over wide but accurate ones, i.e., they prioritize informativeness over accuracy. For instance, in study 3 in [712] participants were asked to choose between two estimates, (A)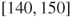 
and (B) 
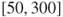. They were told that the correct answer was 159. Most (90%) of the respondents preferred estimate A over B, although only the latter includes the correct answer.
Some researchers found that the format for eliciting interval estimates influences overconfidence. [611] compared overconfidence in interval estimates using three elicitation methods: Range, two-point and three-point. The range method simply asks for, say, a 90% subjective confidence interval. The two-point method asks for a lower limit with a 95% chance of falling below the true value and then an upper limit with a 95% chance of falling above it. The three-point method adds a ‘midpoint’ estimate with a 50% criterion. They found the least overconfidence for the three-point method, and the greatest for the range method. Their explanation is that the two-and three-point methods encourage people to sample their knowledge at least twice whereas the range method is treated by most people as a single assessment of their knowledge base. Other aspect of the task that have been investigated include the extremity of the confidence criterion (e.g., [307] found that tertiles yielded better calibration than more extreme confidence levels), and the nature of the scale used for elicitation (e.g., the study of graininess effects in [713]).
For some time researchers puzzled over the repeated finding that while people are overconfident when they construct intervals, they are reasonably well-calibrated when asked to assign probabilities to two-alternative questions with the same estimation targets [396]. An example of such a task is asking the respondent whether the population of Thailand exceeds 25 million (yes or no) and then asking for the subjective probability that her answer is correct.
A breakthrough came when [706] extended the two-alternative question format to probability judgements about interval estimates provided to the respondent (e.g., estimating the probability that Thailand's population is between 25 million and 35 million). Comparing these judgements with the intervals elicited from respondents with a fixed confidence criterion (e.g., a 90% subjective confidence interval for Thailand's population), they found that overconfidence was nearly absent in the former but, as always, quite high in the latter. These findings have since been replicated in most, but not all, comparison experiments of this kind [500].
Juslin, Winman and Hansson [384] accounted for these and related findings, in part, by noting that while a sample proportion is an unbiased estimate, the sample interval coverage-rate is upwardly biased. Their explanation is that people are ‘native intuitive statisticians’ who are relatively accurate in sampling their own knowledge but treat all sample estimates as if they are unbiased. The clear implication is that subjective probability judgements of intervals provided to respondents are better-calibrated than intervals produced by respondents to match a coverage-rate.
Finally, let us consider partition dependence. On grounds of insufficient reason, a probability of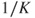 
is assigned to 
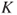mutually exclusive possible events when nothing is known about the likelihood of those events. Fox and Rottenstreich [299] present evidence that subjective probability judgements are typically biased towards this ignorance prior. Thus, probability judgements influenced by the ignorance prior are partition dependent. Fox and Clemen [298] find evidence that this dependence decreases as domain knowledge increases, and that experts in decision analysis are susceptible to it.
Partition dependence poses problems for probability assignments in two respects. First, it may be unjustified because there is a normatively correct partition. For instance, [299] pose the question of how likely Sunday is to be the hottest day of the week. The principle of insufficient reason would suggest that 1/7 is the correct answer, so their demonstration that people can be induced to partition the events into just two possibilities (Sunday is or is not the hottest day) and therefore assign a probability of 1/2 indicates that those people are anchoring onto an incorrect partition.
A more profound difficulty is that partitions may be indeterminate or the sample space may be ambiguous. Consider a bag containing 10,000 marbles whose colours are completely unknown to us. How should we use the principle of insufficient reason to judge the probability of drawing a red marble from this bag? Also, consider a scenario in which we are told that Chris, James and Pat are applying to an engineering firm and are then asked to estimate the probability that each of them is hired by the firm. It is unclear whether there is only one position available or multiple positions. Thus, equally defensible partitions could yield ignorance priors of 1/2 each or 1/3 each. Smithson, Hatori and Gurr [604] present experiments demonstrating that a simple cue asking people to nominate which candidate has the highest probability of being hired induces more people to constrain their probabilities to sum to 1. See also the discussion of the principle of insufficient reason in Footnote 49 of Chapter 7.
In many real-world situations the sample space partition is only incompletely known (e.g., in complex technical systems where not all failure modes have been observed). A seminal study by [291] concerning people's assignments of probabilities to possible causes of a given outcome (e.g., an automobile that will not start) revealed that possible causes that were explicitly listed received higher probabilities than when the same causes were implicitly incorporated into a ‘Catch-All’ category of additional causes. The effect has since been referred to as the ‘catch-all underestimation bias’ and also sometimes the ‘pruning bias’ [549]. In a more general vein, [638] show that unpacking a compound event (e.g., cancer) into disjoint components (e.g., breast cancer, lung cancer, etc.) or repacking its complement tends to increase the perceived likelihood of that event. Partition dependence accounts for this effect as well as the catch-all underestimation bias.
Walley [672] argues that while partition dependence poses a problem for likelihood judgements that yield a single probability, imprecise probability judgements should not depend on the state-space partition. Whether or when imprecise probability judgements are or should be partition-dependent is an open question. Smithson and Segale [606] compared elicited probability intervals with precise probabilities and found that the location of the intervals were as influenced by partition priming as precise probabilities. However, they also found that some respondents constructed wider intervals when they were primed with an incorrect partition, indicating that they still bore the correct partition in mind.
No research appears to have been conducted on ways of dealing with partition dependence in the face of sample space incompleteness or ambiguity. There are several unresolved issues regarding partition dependence, especially where imprecise probabilities are involved. Nevertheless, the literature on partition dependence should remind elicitors to take care in specifying a partition clearly when a preferred partition is available, and to find out which partition(s) respondents have in mind when providing their estimates.
15.4 Matching methods with purposes
What methods can be recommended for eliciting subjective imprecise probabilities? The choice of method will depend in good part on the goals of elicitation and the availability of effective tools for assessing the results. Owing to the many gaps in knowledge about the effectiveness of various elicitation methods, this subsection can only provide some incomplete guidelines.
Beginning with numerical estimation methods, we have seen that three key concerns are diminishing sensitivity to probabilities further away from the 0 and 1bounds, overconfidence, and partition dependence. There are tradeoffs between dealing with these issues and obtaining informative estimates. Evaluations of intervals provided by an elicitor may be better calibrated than intervals produced by respondents, but two obvious shortcomings arise from the fixed interval approach. First, the elicitor cannot specify an a priori confidence-level, and second, the respondent cannot direct the elicitor towards an interval that ‘best’ represents her or his assessment. If a specific confidence-level is desired, [706] recommend an iterative procedure involving the evaluation of a series of intervals that homes in on the appropriate confidence-level. However, this approach does not yield a unique ‘best’ interval.
[698] propose an elicitation method (MOLE, or ‘more or less’) that arguably relies less on absolute judgements than either interval production or interval evaluation methods. Their rationale begins with the arguments in [706] and adds the claim that people are better at relative judgements than absolute ones [310]. Respondents are asked to choose which of two randomly generated numbers is closer to the true value of the quantity to be estimated, and then to judge the subjective probability that their choice is correct. A subjective probability density function is then built up from ten of these choices and confidence judgements, and it is then fitted by a beta pdf. Welsh et al. compared this procedure with three interval production techniques, and found that it nearly eliminated overconfidence. If further investigations of the MOLE technique find that its calibration is comparable to that of the interval evaluation approach then the MOLE would arguably be superior because it yields more information about the respondent's state of knowledge or belief.
Regardless of the numerical estimation method, elicitors will need to be careful about specifying sample space partitions, especially where the partition is incompletely known or ambiguous. The chief dangers here lie in the catch-all underestimation bias and in respondents having unwanted alternative or multiple partitions in mind when they make probability judgements. Elicitors also will need to take into account the diminishing sensitivity issue, especially if some probability intervals include 0 or 1 or bounds close to either of these reference-points while others' bounds are toward the middle of the unit interval.
Verbal probability expressions may not have much to recommend them even when users can agree on a numerical translation, mainly because of the prospect of overconfidence arising from the probability intervals nominated by users. However, the elicitation of such translations could be improved by using interval evaluation instead of interval construction. The most justifiable use of verbal expressions would be among users with an agreed-upon translation in settings characterized by deep uncertainty and a need for rapid communication or decision making.
Finally, utility-based methods (e.g., buying and selling prices or decisional threshold probabilities) could be useful for consistency checks on numerical elicitation results. However, their primary applications would be in settings where such utilities are naturally evaluated. Examples are bid-ask spreads in pricing negotiations,establishment of burden-of-proof or safety standards, and three-option decisional tasks (e.g., go, no-go, wait).
15.5 Further reading
The answer to the question what are the best starting-points in the literature on probability judgements depends on the reader's purpose. Thus, the recommendations provided here will refer to particular topics covered in this review. Beginning with direct numerical elicitation, [500] provides a book-length overview. The classic work on eliciting subjective confidence intervals is [436], with a more recent treatment in [550]. Good reviews and perspectives regarding over- and under-weighting in subjective probabilities are [637] and [317]. Likewise, [713] describes and reviews research on the accuracy-informativeness tradeoff that can influence the width of elicited intervals.
Turning now to psychological influences on probability judgements, the literature on the phenomenon of over-confidence manifested in subjective confidence intervals is exemplified by [396], and recent developments in overcoming this bias may be found in [706] and [384]. The other major influence reviewed here, namely partition priming, is first described in [299] and applied to imprecise probability judgements in [606].
Finally, key works on the topic of words-to-numbers translations of verbal probability phrases are [682, 90, 528]. Issues in the communication of such phrases have been raised by authors such as [89], and a recent paper by [88] describes attempts to improve public understanding of verbal uncertainty expressions employed in the Intergovernmental Panel on Climate Change reports, by interpreting them in terms of imprecise probabilities.