Introduction
One of the big challenges for science is coping with uncertainty, omnipresent in modern societies and of ever increasing complexity. Quantitative modelling of uncertainty is traditionally based on the use of precise probabilities: for each event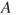 
, a single (classical, precise) probability 
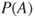is assigned, typically implicitly assumed to satisfy Kolmogorov's axioms. Although there have been many successful applications of this concept, an increasing number of researchers in different areas keep warning that the concept of classical probability has severe limitations. The mathematical formalism of classical probability indispensably requires, and implicitly presupposes, an often unrealistically high level of precision and internal consistency of the information modelled, and thus relying on classical probability under complex uncertainty may lead to unjustified, and possibly deceptive, conclusions.
Against this background, a novel, more flexible theory of uncertainty has evolved: imprecise probabilities. Imprecise probabilities have proven a powerful and elegant framework for quantifying, as well as making inferences and decisions, under uncertainty. They encompass and extend the traditional concepts and methods of probability and statistics by allowing for incompleteness, imprecision and indecision, and provide new modelling opportunities where reliability of conclusions from incomplete information is important.
Given that it is a more flexible, and indeed a more honest description of complex uncertainty, the term ‘imprecise probabilities’ taken literally is an unfortunate misnomer, which, regrettably, has provoked misunderstandings. Nevertheless ‘imprecise probabilities’ has established itself as an umbrella term for related theories of generalized uncertainty quantification, most notably including lower and upper probabilities and lower and upper previsions. There a classical (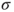
-) additive probability or a classical, linear prevision (expectation) 
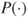is replaced by an interval-valued set-function or functional 
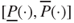. For every gamble (random variable) 
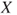, the lower prevision 
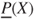and the upper prevision 
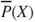have a clear behavioural meaning as (typically different) supremum acceptable buying price and infimum acceptable selling price for 
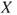, respectively. For events 
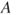, the lower probability 
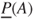can informally be interpreted as reflecting the evidence certainly in favour of event 
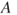, while the upperprobability 
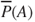reflects all evidence possibly in favour of 
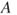. Imprecise probabilities live in the continuum between two extreme cases: the case of classical probabilities and linear previsions where 
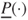and 
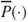coincide, appropriate only if there is complete information on the stochastic behaviour of a perfect precise random process, and on the other extreme, the case of complete probabilistic ignorance, expressed by 
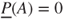and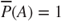 
for all non-trivial events 
.
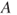Using imprecise probabilities or related concepts seems very natural, and indeed it has a long tradition (see, in particular, [343] for a review). The first formal treatment dates back at least to Boole's book [81] in the middle of the nineteenth century. Further milestones include among others the work of Keynes [394] on incomplete probability orderings; Smith's [602] introduction of lower and upper betting odds and Williams' [702] generalization of coherence; Ellsberg's [264] experiments demonstrating the constitutive role of complex uncertainty in rational decision making; Dempster's [222] concept of multivalued mappings in inference, and its powerful reinterpretation by Shafer [576], that became particularly popular in artificial intelligence (‘Dempster-Shafer theory’ of belief functions); Huber's [367] reflection on the power of capacity-based neighbourhoods models in robust statistics; and Walley and Fine's [678] work on a frequentist theory of lower and upper probabilities.
Walley's book [672] had a boosting impact, it provided a comprehensive foundation for the theory of lower and upper previsions and coined the term ‘imprecise probabilities’. Further influential books include the monographs by Kuznetsov [414], Weichselberger [692] on an introduction of interval probability in generalization of Kolmogorov's axioms, and Shafer and Vovk [582] developing game-theoretic probability.
Based on this solid foundation, work on imprecise probabilities has been gathering strong momentum, and their high potential should be clear in any area of application where the reliability of conclusions drawn from reasoning under uncertainty is of major concern. As a consequence, the literature is spread widely over different fields, each with its own journals and conferences. The Society for Imprecise Probability: Theories and Applications (SIPTA, www.sipta.org) provides an umbrella over these activities, also organizing biennial summer schools and the biennial ISIPTA symposia1, which since 1999 have been fostering the exchange of the cutting-edge research on imprecise probabilities.
Given the increasing interest in imprecise probabilities, the time is right to present an overview of the main aspects of imprecise probabilities theory and applications. In graduate teaching, research and consultancy, we felt there was a need for an introductory book on imprecise probabilities. The present book aims at filling this gap, and it attempts to achieve this by a providing a synthesis between a book as a holistic entity and a collection of contributions on the current state of the art by leading researchers. We have first established a common structure and a concise framework including a unique notation, and then, in order to cover the most important areas of the vastly developing field, we have asked specialists for specific contributions within this framework, emphasizing continued exchange with the other chapter authors and the editors. The book shows the current state of the art, it sets out research challenges on theory and applications of imprecise probabilities and it provides guidance for further reading.