The circle is the embodiment of geometrical perfection: smooth everywhere, harmonious and symmetrical. It is the locus of a point equidistant from a centre, the simplest two-dimensional shape there is. But when we divide the distance around the circle (the circumference) by the distance across it (the diameter), we hear a scream:
3.141592653589793238462643383279502884197169399375105820974944592307816406286208…
This number, the numerical value of the circumference divided by the diameter, is constant for all circles and its decimal digits continue for ever with untamed insubordination. In the eighteenth century the number gained its own name and symbol, pi, or π, and it has become a cross-cultural icon, the most famous constant in science and a metaphor for the inscrutability of the universe. Everyone learns it at school and for many it is the only thing they remember about mathematics.
Now here’s the thing.
Pi is wrong.
The calculation is correct, of course. The ratio ![]() is evidently the above number beginning 3.14. Pi is wrong because it is an
inappropriate number to represent the circle. Pi is an imposter, a false idol undeserving of its international acclaim.
is evidently the above number beginning 3.14. Pi is wrong because it is an
inappropriate number to represent the circle. Pi is an imposter, a false idol undeserving of its international acclaim.
Or so wrote Bob Palais, an American mathematician, in 2001. He argued that a much better choice for the circle constant would be the ratio ![]() , because the radius, the distance from the centre to the side, is a much more fundamental concept than the diameter. Many agree with him, including me. Look at our definition of the circle
in the opening paragraph. The circle is a fixed distance, the radius, rotated around a centre. The diameter, or width, is an afterthought. Mathematics is a quest for elegance, clarity and
correctness, and it is unfortunate that the most famous number in maths does not reflect the truth about circles in the clearest, most elegant and most correct way. (At school we are taught the
word ‘diameter’ purely to understand pi, and once we have learned what it means we never return to it. Mathematicians always take for granted that the diameter is just the radius times
two.)
, because the radius, the distance from the centre to the side, is a much more fundamental concept than the diameter. Many agree with him, including me. Look at our definition of the circle
in the opening paragraph. The circle is a fixed distance, the radius, rotated around a centre. The diameter, or width, is an afterthought. Mathematics is a quest for elegance, clarity and
correctness, and it is unfortunate that the most famous number in maths does not reflect the truth about circles in the clearest, most elegant and most correct way. (At school we are taught the
word ‘diameter’ purely to understand pi, and once we have learned what it means we never return to it. Mathematicians always take for granted that the diameter is just the radius times
two.)
In 2010 Michael Hartl, a Silicon Valley entrepreneur, ratcheted up anti-pi sentiment by baptizing the ratio ![]() with the Greek letter
tau, or τ. Tau is twice pi because the circumference fits twice as many radiuses around it as it does diameters. In other words:
with the Greek letter
tau, or τ. Tau is twice pi because the circumference fits twice as many radiuses around it as it does diameters. In other words:
τ = 2π = 6.283185307179586476925286766…
Just like pi, tau’s decimal expansion is infinite and follows no known pattern.
In the Tau Manifesto, Hartl encourages young mathematicians to replace pi with tau in their work. A start would be to preface all papers with ‘For convenience, we set τ = 2π’. He warns that the fight will be long because the foe is so powerful, the beneficiary of centuries of propaganda. ‘Some conventions, though unfortunate, are effectively irreversible,’ he writes. ‘[But] the switch from π to τ can … happen incrementally; unlike a redefinition, it need not happen all at once.’
The symbol τ is triply clever. It looks like a one-legged π, so if we see these symbols as fractions where the number of legs is the denominator – that’s the number under the
line – then τ really is twice π, since a quantity divided by 1 is twice something divided by 2. Tau also works as an abbreviation for ‘turn’, in the same way that pi was
originally an abbreviation for ‘periphery’. And just as pi is a delicious homonym of pie, a dish most often presented in circular form, so too is tau of Tao, the Chinese spiritual path
whose symbol ![]() , the yin and yang, expresses harmony and movement within the circle.
, the yin and yang, expresses harmony and movement within the circle.
The Tau Manifesto makes a serious point in a light-hearted way. The quintessence of a circle is the turn of its radius, not the span of its width. Indeed, the dynamic properties of a circle, as exemplified by the wheel, are the mechanical ground rules on which civilization is based. In this chapter you will learn that the three most important things about circles are rotation, rotation, rotation.
Let’s roll.
The path of a point on a rolling wheel may be unlike any curve you have seen before. It certainly was for Galileo, who named it the ‘cycloid’ and was the first to study it in any depth. The father of modern mechanics, Galileo was naturally drawn to curves that originate mechanically. The wheel moves smoothly, yet creates a curve with sharp spikes, the cusps, where its direction reverses. Each hump corresponds to one full rotation, the completion of a cycle. The cycloid looks less like a curve than a queue of sleeping tortoises.

The cycloid.
In the illustration I have marked the position of the point at each quarter-turn, and you can see quite clearly that it covers more distance when it’s in the upper half of the wheel than when it’s in the lower half. The wheel moves in two ways: horizontally along the ground and rotationally around its centre, and both motions combine differently throughout the cycle. If the wheel is rotating at constant speed, the point on the wheel reaches its highest speed with respect to the ground at the crest of the cycloid, and its lowest at the cusp, where it reaches zero instantaneously before accelerating again. It is startling to realize that for any rolling wheel – even one on a racing car doing 200mph – the point in contact with the ground is stationary. Painters know that the top half of rolling wheels go faster than the bottom halves, which is why they often draw the top half of a moving wheel blurred and the bottom half in focus. Likewise, the spokes of a rolling bicycle wheel are often only visible near to the ground, where they are moving slowly enough to be seen.
A train wheel consists of two discs, one that sits on the track, and the rim, or flange, which dips over the side. A point on the flange will trace a curve that curls back on itself when below the level of the track, as shown in the illustration. On all trains, therefore, there are always points on the wheel that are going against the direction of travel.

The path of a point on a train wheel.
Never in the history of mathematics has a curve been the object of such frenzied attention as the cycloid was in the seventeenth century. So beautiful its shape and so bitter the squabbles among its admirers that it gained a reputation as the ‘Helen of geometers’. Suitor numero uno, Galileo, was practical in his advances. He cut the shape of the curve from a piece of material and judged it to be pi times heavier than a piece of the same material cut in the shape of the generating circle. He concluded that the area under the curve was therefore pi times the area of the circle. He was close – but wrong. The area is exactly three times larger, a result proved later by the French mathematician Gilles Personne de Roberval.
Roberval (1602–75) proved many theorems about the cycloid but did not publish any of them. To keep his position as professor of mathematics at the Collège de France, the country’s most prestigious seat of learning, he had to provide the best answer to a problem announced publicly every three years. Roberval, as professor, also set the problems, which meant he had no incentive to share his results lest they help potential rivals with an eye on his job. His position gave him prestige and a salary, but castrated his legacy. He is probably the least remembered of the great French mathematicians. He was also famously irascible, and became bitterly frustrated when others announced results he claimed to have proved already. When his friend, the Italian Evangelista Torricelli, published the first treatise on the cycloid in 1644, a fuming Roberval dispatched a letter accusing him of plagiarism. Torricelli died three years later, of typhoid, but a rumour circulated that his death was due to the shame of being accused of such dishonour.
One evening in Paris in 1658, Blaise Pascal lay awake in bed tormented by a vicious toothache. Once a celebrated mathematician, Pascal had abandoned maths to concentrate on theology and philosophy. To take his mind off the pain, he decided to think about the cycloid. Miraculously, the toothache disappeared. Surely, he thought, it was a nudge of encouragement from God that he should continue to investigate this divine curve. He thought about the cycloid for eight industrious days, discovering many new theorems. Rather than publishing them, however, he turned them into an international challenge. He invited colleagues to prove some of his results, offering forty Spanish gold pieces for first prize and twenty for second. Only two mathematicians answered his call, John Wallis in England and Antoine de Laloubère in France. But their submissions contained errors, so Pascal did not award the prize, enraging both men. Instead he published his results in a pamphlet. He also received a letter from Christopher Wren, which demonstrated a fact of which the Frenchman was unaware. Wren had answered possibly the most basic question you can ask about the cycloid: how long is it? Wren showed that it is exactly eight times the radius of the generating circle. When Roberval found out, of course, he was incensed, insisting he had proved this assertion years before.
The cycloid’s allure grew even more when Christiaan Huygens discovered a remarkable mechanical property it possessed. The Dutch scientist was experimenting with pendulums as a new basis for the design of clocks. A simple pendulum is a piece of string with a bob at the end of it, as illustrated below left. The bob’s path is a circular section and the further it swings from the vertical position the longer it takes to complete a full swing. To use a pendulum for timekeeping, however, Huygens wanted the bob to complete each swing in an equal time interval regardless of how wide the swing was. Inspired by his friend Pascal’s challenge, he realized that the path he was looking for was none other than an upside-down cycloid, illustrated below right, and that this path could be achieved by placing two cycloid ‘cheeks’ at the top of the pendulum. When the pendulum swings, its string bends around each cheek, pulling the bob from its circular path into a cycloidal one. However far from the centre the bob swings on a cycloidal pendulum, it takes exactly the same amount of time to return to its starting point.

A simple pendulum, and one swinging between two cycloids.
Another way to marvel at this property is to imagine balls sliding down a frictionless track which is in the shape of an upside-down cycloid, as shown below. All balls take exactly the same time to reach the bottom, irrespective of their starting positions. A ball placed higher up starts off on a steeper slope than a ball starting at a position on the curve below it, giving it greater initial acceleration, and therefore a higher speed. The two balls will collide precisely at the bottom of the curve. When the cycloid was heralded as ‘the path of equal descent’ – or the tautochrone, from the Greek tauto, meaning ‘same’, and chronos, meaning ‘time’ – scientists were smitten all over again.
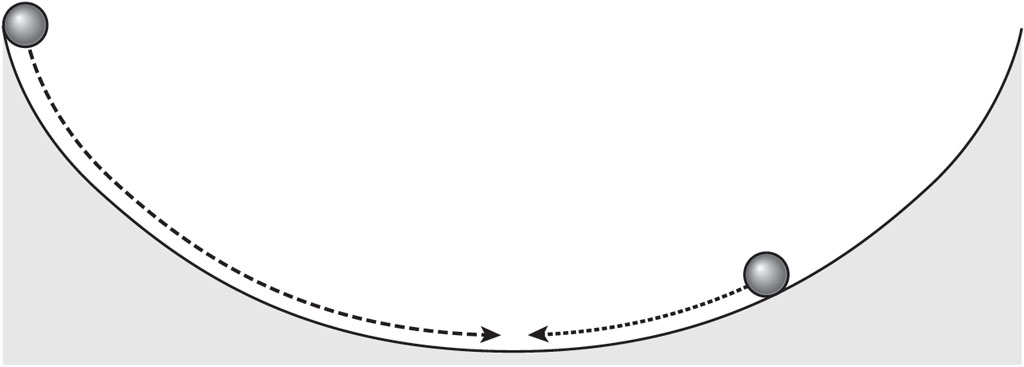
The path of equal descent.
The apogee of the curve’s narrative arc came as the seventeenth century drew to a close. An article in the Acta Eruditorum, a new scientific periodical printed in Leipzig, trumpeted:
I, Johann Bernoulli, address the most brilliant mathematicians in the world. Nothing is more attractive to intelligent people than an honest, challenging problem, whose possible solution will bestow fame and remain as a lasting monument … If someone communicates to me the solution of the proposed problem, I shall publicly declare him worthy of praise.
The problem of which he spoke – and to which he already knew the answer – was this question: What is the path of quickest descent? Or, what is the shape that a frictionless slide must be in order to get an object from one point to another in the quickest time? The desired curve was nicknamed the brachistochrone, from the Greek brachistos, meaning ‘shortest’, and chronos, meaning ‘time’. Bernoulli said that the curve was not a straight line, but was nevertheless well-known. Hint! The answer, if you haven’t guessed already, was the cycloid. The illustration below shows the fastest descent between the points A and B, and between A and C. Since the cycloid has only one shape, the curve must be scaled to fit, depending on the relative positions of the start and end points. The path may only drop, as it does between A and B, or it may drop and then rise, as it does between A and C.

The path of fastest descent.
When the path drops and rises, the advantages of a steeper and longer drop at the start outweigh the slowing effect of the rising curve at the end. If you make a model of an upturned cycloid, and roll a metal ball down it from, say, point A to point B while simultaneously rolling a ball down a straight slide (the dashed line) from A to B, the effect is striking, even though you know which ball will win. Compared to the speedy ball descending the cycloid, the ball descending the straight edge looks like it is rolling through mud. From the eighteenth century onwards, universities and museums started building wooden cycloids to demonstrate the brachistochrone. These models could equally demonstrate the autochrone: place a ball on each side of the upturned cycloid and, regardless of where they start, the balls will knock into each other at the bottom-most point.
After six months Bernoulli had received only one correct response to his challenge, from his German friend Gottfried Leibniz. So he published a new appeal for entries in the Acta, noting the absence of ‘those who boast that through special methods … they have not only penetrated the deepest secrets of geometry but also extended its boundaries in marvellous fashion’. The remark was a jibe at Isaac Newton and his method of fluxions, a powerful new mathematical tool that promised to solve problems like the brachistochrone, and which we will cover in a later chapter. Bernoulli sent Newton a copy of the Acta to make sure he got the message. Newton was in his fifties at the time, no longer a Cambridge professor but instead in charge of the Royal Mint at the Tower of London. He read Bernoulli’s letter after arriving home tired from work, and did not go to sleep until he had nailed the answer, at four o’clock in the morning. ‘I do not love … to be … teezed by forreigners about Mathematical things,’ he grumbled. Newton submitted his entry anonymously. Upon reading it Bernoulli is said to have declared ‘ex ungue leonem’ – ‘I recognize the lion by his claw.’
And so the cycloid, already the subject of so many quarrels, became the flashpoint of an early skirmish in the greatest feud in Enlightenment science. Newton’s fluxions were mathematically equivalent to Leibniz’s infinitesimal calculus, and, as we will see, a nasty priority dispute developed between both men that set the English and European scientific communities against each other for a century. The egos of men, however, did nothing to tarnish the sanctity of the curve. On the title page of Bernoulli’s collected works is a picture of a dog gazing lovingly at a cycloid, together with the motto Supra invidiam – above envy.
Since the cycloid is the path of quickest descent, you might think it would be the favoured shape for a skateboard ramp. Yet as far as I can discover only one exists, built by the French artist Raphaël Zarka in New York in 2011 as part of a project mixing physics, sculpture and public spaces. The skaters did not like it, since it felt so unusual. ‘If I were a completely round ball-bearing dropped from the top of the cycloid ramp, I would probably be able to better gauge the true ascent and descent,’ said skate writer Ted Barrow, ‘but as a skateboarder who has struggled with mastering a set of skills that all come down to attempting to maintain balance and NOT fall off his skateboard when speed increases, my experience was more about adjusting the speed, and suiting my movements to the strange curves of the walls, than experiencing the fastest descent.’ The cycloid skateboard ramp, he added, is unlikely to catch on.
The cycloid belongs to a family of curves called the ‘roulettes’, each made by the path of a point on a rolling wheel. Roulettes roll on all terrains. The path of a wheel rolling around a circle of identical size is a cardioid, illustrated below left, so-called because it looks like a heart. The path of a wheel rolling around a circle with twice its radius is a nephroid, illustrated in the centre, which looks like a pair of kidneys. The illuminated buttocks in your mug of tea when it’s placed near a bright window are two half kidneys of a nephroid, since that is the shape produced by horizontal light reflecting off the inside of a circle, illustrated on the right.
The first machine that drew curves for aesthetic as well as scientific reasons drew roulettes. The ‘geometric pen’, invented by the Italian Giambattista Suardi in the eighteenth century, consisted of a tripod with a rotating arm, on which a rotating cog held a pencil. ‘There never was, perhaps, any instrument which delineates so many curves as the geometric pen,’ gushed George Adams Jr., Instrument Maker to King George II. The designs were baroque and magical. In the nineteenth century P. H. Desvignes of Vienna designed a roulette-drawer he called the ‘spirograph’, which engraved the curves on a copper plate using a diamond stylus. The machine was used to create elaborate patterns for banknotes, to prevent forgeries. Drawing roulettes with a plastic set of cogs called the Spirograph, a toy launched in 1965, remains a rite of passage for nerdy kids.
One of my favourite pub maths puzzles involves rolling one coin around another. Put two identical coins next to each other flat on a table, as below, with the heads both upright. Roll the left coin around the right. What is the position of the head when the left coin reaches the right side?

Rolling with money.
When I was first asked this question, I assumed that the rolling coin would be upside down, as it has only gone halfway around the fixed coin. I was wrong. The Queen completes a full revolution. It’s a strange and counterintuitive experience to see her spin with regal speed, as if desperate to maintain her dignity in an upright position. The movement is a result of the property of all roulettes: they combine two independent directions of motion. In this case the coin is rotating around itself but also around the other coin. For every degree the left coin rolls around the right coin, it rotates two degrees around itself.
We generate roulettes by rolling a wheel. We can also generate curves by spinning a wheel with a fixed centre. These curves are mathematically simpler than roulettes, since we are only concerned with one direction of motion, the rotation about the centre.
Consider a point on the rim of a wheel spinning anticlockwise, illustrated below (i). If we plot its height relative to the angle of rotation when projected along a horizontal axis, we get a curve called the ‘sinusoid’ or ‘sine wave’. I have marked the point on the circle at 0, 45, 90, 225 and 270 degrees. The sinusoid peaks at 90 degrees, returns to the horizontal axis at 180 degrees, then heads below the axis and is back where it started after a full turn. If the wheel keeps spinning, the curve will repeat once every rotation, painting symmetrical undulations ad infinitum.
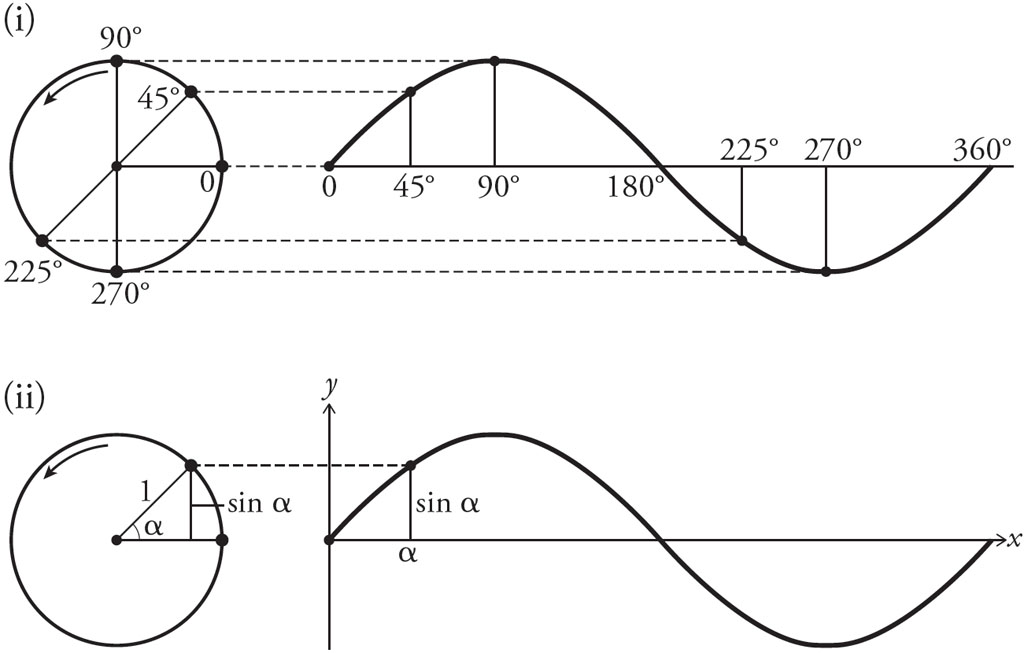
The variation in height of a rotating point, with respect to the angle it has rotated, generates a sine wave.
(You may be wondering why this wiggly wave is named after the sine, the ratio between two sides of a right-angled triangle, since waves are nothing like triangles. It all makes sense, however,
when we remember that the concept of sine comes from the circle in the first place: it is the half-chord. In the illustration (ii) above, we see this more clearly by creating a right-angled
triangle in the wheel. If we let the hypotenuse be 1, then sin ![]() height of point.)
height of point.)
The first person to draw a sinusoid was Gilles de Roberval in the seventeenth century. He called it the cycloid’s ‘companion curve’. The companion would later become pre-eminent in the hearts (and ears) of scientists and mathematicians.
The sinusoid is what’s called a ‘periodic wave’, an entity in which a curve repeats itself again and again along the horizontal axis. The sinusoid is the simplest type of periodic wave because the circle, which generates it, is the simplest geometrical shape. Yet even though it is such a basic concept, the wave models many physical phenomena. The world is a carnival of sinusoids. The vertical position over time of a weight bouncing up and down on a spring is a sinusoid, as shown below left. The weight moves fastest in the middle of the oscillation, and slows down when it reaches the top and bottom, giving the recognizable shape (thinner here, since the horizontal scale is reduced). The horizontal position over time of a pendulum swinging side to side is also, for small swings, a sinusoid. Imagine a pendulum bob filled with fine sand that falls through a hole in the bottom, as shown below right. A bob swinging north–south leaving a deposit on a conveyor belt moving east–west will draw out a sine wave. Objects like the spring and the pendulum, which oscillate in sinusoids over time, are said to exhibit ‘simple harmonic motion’.

A weight on a spring bounces, and a pendulum swings, with ‘simple harmonic motion’.
We saw earlier that roulettes draw pretty patterns. So do sinusoids. In the 1840s, the Scottish mathematician Hugh Blackburn was experimenting with a sand-filled pendulum. He decided to hang the bob from two cords hanging in a Y, as illustrated below, joined by a ring at r. He held the ring still and swung the bob from left to right. Then he pulled the ring forwards and let it go, making it also swing forward and back. The bob was therefore being guided by two perpendicular swings, and the result was spectacular. The two competing sinusoidal motions pushed and pulled each other in a mathematical pas de deux that produced a sand pattern underneath of stunning intricacy. It was not long before enterprising instrument makers were manufacturing machines called harmonographs, in which two pendulums oscillated a pen simultaneously in two different directions. The user of the harmonograph would adjust the length of the pendulums, set the amplitude of their swings, and then release them when the pen was positioned on a piece of paper. As the pen looped and swirled it traced beautiful geometrical shapes that were mechanical, yet somehow felt alive.
The Victorian harmonograph looked like a cross between a desk cabinet and a grandfather clock. Watching the pen create the images was hypnotic, a performance as much as a process. The loss of energy through friction, or ‘damping’, created curves that spiralled inwards as they headed towards the stationary point of equilibrium. Some of the larger machines were able to keep swinging for an hour or more before the pendulums came to a standstill.
The harmonograph was so popular that many other machines were manufactured based on the same principle: the sympalmograph, the pendulograph, the duplex pendulum, the quadruple harmonic-motion pendulum and, in the early twentieth century, the Creighton Compound Harmonic Motion Machine and the photo-ratiograph, which rendered the curves on photographic paper with a moving point of light. In the 1950s, the American artist John Whitney built a harmonograph out of Second World War military junk. He bought an M5 anti-aircraft director – a large metal box of cranks and levers that amounted to an early analogue computer used to calculate which way to fire at planes – and customised it so that the rotating parts could move a stylus with simple harmonic motion in two directions. Whitney could adjust the speed and size of the sinusoids electronically, giving him much more control and eliminating the effects of damping. The patterns he produced were dazzling and became some of the most iconic images in the history of mathematical art. They were famously used in the title sequence and posters for Alfred Hitchcock’s 1958 movie Vertigo; the swirling, dizzying concentric loops were a perfect visual metaphor for the film’s tormented inner landscape. Not only were Whitney’s patterns the first computer-generated images to feature in a Hollywood film, but his electronic harmonograph was also the first ever computer-animation machine.
Around the time that harmonographs became all the rage in Victorian drawing rooms, a physicist in Paris realized that he could generate identical figures using two tuning forks and a beam of light. The demonstrations by Jules Antoine Lissajous were some of the most beautiful experiments of the nineteenth century. When a tuning fork makes a sound, the metal prongs oscillate with simple harmonic motion. Lissajous attached a small mirror to one tuning fork and shone a beam at it so that it was reflected to a point on a screen. When the fork was made to vibrate, the point elongated into a horizontal line. The point was oscillating very fast back and forth, but the spectators saw it as a line because the image of the dot at each point persists in our vision for a split second longer than it is actually there. Lissajous then introduced a second tuning fork, which also had a mirror attached. The second fork was positioned at right angles to the first, so the light beam was reflected from the mirror on the first fork, oscillating in one direction, to the mirror on the second fork, oscillating in a perpendicular direction, and then onto the screen. The forks, in other words, were acting like the pendulums in a harmonograph, moving the beam in two competing sinusoidal oscillations. Yet instead of oscillating once every second or so, they were oscillating hundreds of times a second. Audiences saw striking images on the screen, which are now called Lissajous figures.
Different combinations of tuning forks produce different curves. When two identical tuning forks are played at the same volume, the sinusoids are equal and the curve looks like one from the first row of pictures shown below: an ellipse, a line or a circle. The particular curve depends on where each oscillation starts relative to the other. Lissajous adjusted this by changing the distance between the forks. When one fork oscillates at twice the frequency of the other, the curve is from the second line of images: a parabola or a figure of eight. The remaining rows in the illustration show Lissajous figures for other whole-number ratios between the frequencies of the sinusoids. When the ratio of the frequencies cannot be described by two whole numbers, the beam will never return to the starting point and the image will be a blur.
Lissajous figures, taken from a book published in 1875: for each row, the ratio between the frequencies of the sinusoids is marked in the left column.
The frequency of the oscillation of a tuning fork determines its note. A fork that oscillates at about 262 waves per second, for example, is middle C. Lissajous’ experiments thus provided the music industry with an improved method for calibrating tuning forks. Rather than using your ear to hear whether two forks are in tune, you could use your eyes. Craftsmen set up beams of light in their workshops. If the pitches of the two forks were slightly off, their frequencies were also slightly off, and the curve made by doubly reflecting the beam was a mess. The technicians would use one fork as the standard, and then file down the other until the figure on the wall was an ellipse, indicating that the note was the same.
Lissajous figures are the result of combining two perpendicular sinusoidal oscillations. Can we combine sinusoids that are oscillating on the same axis?
Absolutely! And it leads to some of the richest and most useful theorems in mathematics. To help us along, let me define three concepts that are vital when talking about waves: frequency, amplitude and phase. Frequency is the number of times a wave oscillates in a set interval, amplitude is the vertical height between peak and trough, and phase is a measure of the horizontal position.
Armed with these concepts, we can outline an arithmetic of sinusoids, with the illustration below:

(i) This curve is the basic sine wave, with the equation y = sin x.
(ii) When we double the frequency, which means that the wave repeats itself twice in the period that it takes the original curve to complete once, the equation becomes y = sin 2x.
(iii) When we double the amplitude, which means that the wave oscillates twice as high, the equation is y = 2 sin x.
(iv) When we alter the phase by shifting the wave a quarter of a wave to the left, we get the basic cosine wave, y = cos x.
The waves produced by changing the frequency, amplitude and phase of a sinusoid are all sinusoids. A helpful way to think about frequency, amplitude and phase is to remember that sinusoids are generated by a rotating point: the speed of the rotation determines the frequency, the radius of the rotating circle determines the amplitude and the point’s starting position determines the phase.
(v) Here I have added the basic sine wave to the basic cosine wave. When we add two waves together, we just add the vertical values for each point on the horizontal axis. Magically, the result of adding the sine and cosine waves together is also a sinusoid, although one that has a different phase and an amplitude of ![]() . In fact,
whenever two sinusoids with the same frequency are added together the result is always a sinusoid, whatever their amplitudes and phases.
. In fact,
whenever two sinusoids with the same frequency are added together the result is always a sinusoid, whatever their amplitudes and phases.
In other words, a sinusoid added to any number of sinusoids that have the same frequency but different amplitudes and phases remains sinusoidal, like a science fiction monster that always remorphs into its original form. We’ll return to the arithmetic of rotating points shortly, but first let’s take a brief detour to another type of revolution, the French one.
In 1798 Joseph Fourier, a 30-year-old professor at the École Polytechnique in Paris, received an urgent message from the Minister of the Interior informing him that his country required his services, and that he should ‘be ready to depart at the first order’. Two months later, Fourier set sail from Toulon as part of a 25,000-strong military fleet under the command of General Napoleon Bonaparte, whose unannounced objective was the invasion of Egypt.
Fourier was one of 167 eminent scholars, the savan, assembled for the Egyptian expedition. Their presence reflected the French Revolution’s ideology of scientific progress, and Napoleon, a keen amateur mathematician, liked to surround himself with colleagues who shared his interests. It is said that when the French troops reached the Great Pyramid at Giza, Napoleon sat in the shade underneath, scribbled a few notes in his jotter and announced that there was enough stone in the pyramid to build a wall three metres high and a third of a metre thick that would almost perfectly encircle France. Gaspard Monge, his chief mathematician, confirmed that the General’s estimate was indeed correct.
(The Great Pyramid has sides of length 229m and a height of 146m. France is roughly a rectangle 770km north–south by 700km east–west. With these figures Napoleon’s estimate is only 3 per cent off.)
Fourier assumed many administrative roles in Egypt, the most prominent being permanent secretary of the Cairo Institute, a cultural heritage centre modelled on the Institut de France in Paris. When the Institute decided to collate all its scientific and archaeological discoveries, eventually published as the 37-volume Description de L’Égypte, Fourier wrote the introduction. He was, in effect, the father of Egyptology.
On Fourier’s return from Egypt, Napoleon appointed him prefect of the Alpine department of Isère, based in Grenoble. Always a man of fragile health, with extreme sensitivity to cold, Fourier never left home without an overcoat, even in the summer, often making sure a servant carried a second coat for him in reserve. He kept his rooms baking hot at all times. In Grenoble, his academic research was also preoccupied with heat. In 1807 he published a ground-breaking paper, On the Propagation of Heat in Solid Bodies. In it he revealed a remarkable finding about sinusoids.
Fourier’s famous theorem states that every periodic wave can be built up by adding sinusoids together. The result is surprising. Fourier’s contemporaries met it with disbelief. Many waves look nothing at all like sinusoids, such as the square wave, illustrated below, which looks like the crenellations of a castle parapet. The square wave is made up of straight lines, whereas the sinusoid is continuously curved. Yet Fourier was right: we can build a square wave with only sinusoids.
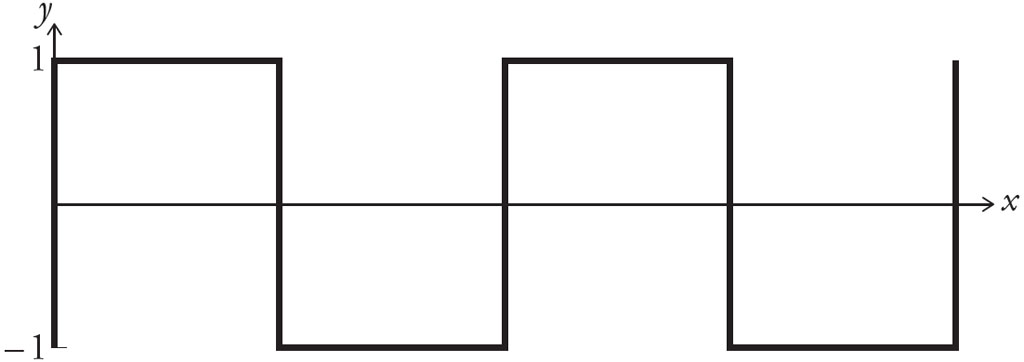
Here’s how. In the illustration below there are three sine waves: the basic wave, a smaller sine wave with three times the frequency and a third of the amplitude, and an even smaller sine
wave with five times the frequency and a fifth of the amplitude. We can write these three waves as sin x, ![]() , and
, and ![]() .
.

In the illustration below I have started to add these waves together. We see the basic wave, sin x. The sum sin x + ![]() is a wave that looks like a row of molar teeth. The sum sin x +
is a wave that looks like a row of molar teeth. The sum sin x + ![]() +
+ ![]() is a wave that looks like the filaments of a light bulb. If we carry on adding terms of the series:
is a wave that looks like the filaments of a light bulb. If we carry on adding terms of the series:
![]()
we will get closer and closer to the square wave. At the limit, adding an infinity of terms, we will have the square wave. It is stunning that such a rigid shape can be constructed using only undulating wiggles. Any periodic wave consisting of jagged lines, smooth curves, or even a combination, can be built up with sinusoids.

The sum of sinusoids that make up a wave is called its ‘Fourier series’. It’s a remarkably useful concept since it allows us to understand a continuous wave in terms of discrete signals. The terms in the series for the square wave, for example, can now be represented by the bar chart below.

The horizontal axis represents the frequencies of the constituent sinusoids, and the vertical axis their amplitudes. Each bar stands for a sinusoid, and the leftmost bar is the sinusoid that has the ‘fundamental’ frequency. This type of graph is known as the ‘frequency spectrum’, or ‘Fourier transform’, of the wave.
Fourier’s theorem was one of the most significant mathematical results of the nineteenth century because phenomena in many fields – from optics to quantum mechanics, and from seismology to electrical engineering – can be modelled by periodic waves. Often, the best way to investigate these waves is to break them down into simple sinusoids. The science of acoustics, for example, is essentially an application of Fourier’s discoveries.
Sound is the vibration of air molecules. The molecules oscillate in the direction of travel of the sound, as shown in the illustration that follows, forming alternate areas of compression and rarefaction. The variation in air pressure at any point over time is a periodic wave.
As you can see, the clarinet wave is jagged and complicated. Fourier’s theorem tells us, however, that we can break it down into a sum of sinusoids, whose frequencies are all multiples of the ‘fundamental’ frequency of the first term. In other words, the wave can be represented as a spectrum of frequencies with different amplitudes. The picture that follows shows the frequency spectrum of the clarinet wave as a bar chart.
Remember, the jagged wave and the bar chart represent exactly the same sound, but in each image the information is encoded differently. For the wave, the horizontal axis is time, whereas on the bar chart the horizontal axis is frequency. Sound engineers say that the wave is in the ‘time domain’, and the transform is in the ‘frequency domain’.
The frequency domain also provides us with all the information we need to recreate the sound of a clarinet using only tuning forks. Each bar in the bar chart represents a sinusoid oscillating at a fixed frequency. Now recall Lissajous’ experiments with tuning forks from earlier in this chapter. The sound wave made by a tuning fork is a sinusoid. So, in order to recreate the sound of a clarinet, all that is required is to play a selection of tuning forks at the correct frequencies and amplitudes described by the bar chart. Likewise, the frequency spectrum of a violin would provide us with instructions on how to use tuning forks to produce the sound of a violin. The difference in timbre between middle C when played on the clarinet and the violin is the result of the same set of tuning forks oscillating with different relative amplitudes. A consequence of Fourier’s theorem is that it is theoretically possible, therefore, to play the complete works of Beethoven with tuning forks, in such a way that is audibly indistinguishable from a symphony orchestra.
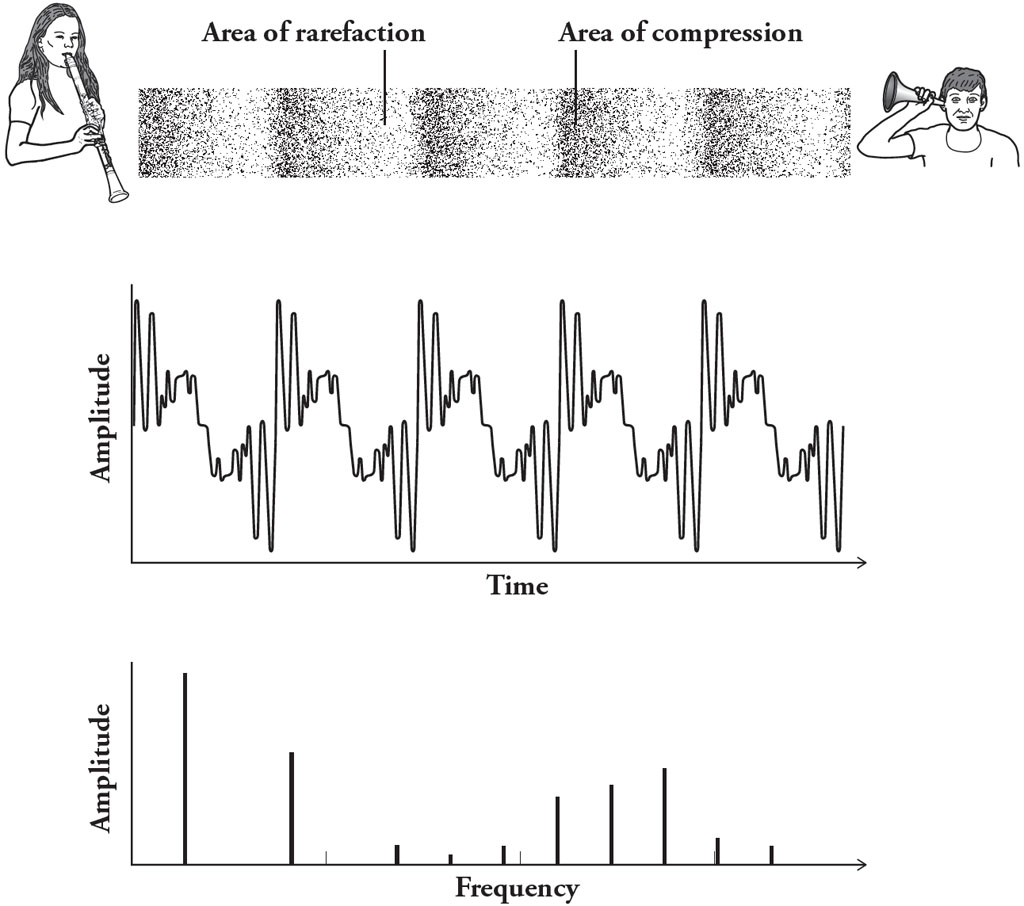
The sound wave and frequency spectrum of a clarinet.
When a fire engine passes Dolby Laboratories in San Francisco, everybody clasps their ears – especially the ‘golden ears’, those members of staff with exceptional hearing – hoping to protect their auditory faculties from deleterious noise. Dolby built its reputation on noise reduction systems for the music and film industries, and it now creates sound quality software for consumer electronic devices, using technology based entirely on sinusoids.
The benefit of being able to switch a sound wave from the time domain to the frequency domain is that some jobs that are really difficult in one domain become much simpler in the other. All sound played out of digital devices – such as your TV, phone and computer – is stored as data in the frequency domain, rather than the time domain. ‘The waveform is like a noodle,’ Brett Crockett, senior director of research sound technology, told me. ‘You can’t grab it.’ Frequencies are much easier to store because they are a set of discrete values. It also helps that our ears cannot hear all frequencies. ‘[Ears] don’t need the whole picture,’ Crockett added. Dolby’s software turns sound waves into sinusoids, and then strips out nonessential sinusoids so that the best possible sound can be recorded and stored with the least possible information. When the information is played back as sound, the spectrum of remaining frequencies is reconverted into a wave in the time domain.
It sounds easy, but in practice the task of filleting sinusoids from the frequency spectrum is exceedingly complex. It relies, firstly, on what’s called a Fast Fourier Transform, a computer algorithm that converts the wave into its frequencies in real time. Secondly, different instruments, musical styles and voices require different solutions. One of the hardest sounds to get right is the harmonica, because its frequency spectrum looks like a picket fence – the amplitudes of the different frequencies are at the same height, forcing you to delete frequencies you can hear. For all Dolby’s state of the art knowhow, the piece of music its software struggles most to recreate faithfully is Moon River, Henry Mancini’s hauntingly beautiful 1961 song. Brett Crockett’s golden ears judge new Dolby technology based on how faithfully it plays a harmonica riff recorded more than half a century ago.
Joseph Fourier was the first person to transform a periodic wave into a spectrum of frequencies. Much later, biologists figured out how the ear works. The part that hears is the cochlea, a tube full of liquid and lined with hair cells, coiled in the inner ear. The hairs vibrate according to the frequency of the incoming sound wave, with the lowest frequencies vibrating hairs at one end of the cochlea, and the highest frequencies vibrating hairs at the other. If we uncoiled the cochlea into a straight line it would look like the horizontal axis of a Fourier transform. Nature has been isolating the frequencies of sound waves for as long as creatures have had ears to hear.
This chapter has been about the maths of going round in circles. Let’s break the cycle. What happens to things that get bigger and bigger and bigger?