In Boulder, Colorado, I visited the man who has given what is arguably the most performed lecture in the history of science. Albert Bartlett, emeritus physics professor at the University of Colorado, premiered his talk Arithmetic, Population and Energy in 1969. By the time I met him, he had given it 1712 times, and despite being almost ninety was continuing at a rate of about 20 times a year. Bartlett has a tall, robust physique and an imposing dome of a head, and he was wearing a Wild West bolo tie with stars and a planet emblazoned on its clasp. In his famous lecture, he proclaims with ominous portent that the greatest shortcoming of the human race is its inability to understand exponential growth. This simple but powerful message has in recent years propelled him to online stardom: a recording of his talk on YouTube, entitled The Most IMPORTANT Video You’ll Ever See, has registered more than five million views.

Exponential (or proportional) growth happens when you repeatedly increase a quantity by the same proportion; by doubling, for example:

1, 2, 4, 8, 16, 32, 64 …

Or by tripling:

1, 3, 9, 27, 81, 243, 729 …

Or even increasing by just one per cent:

1, 1.01, 1.0201, 1.0303, 1.0406, 1.05101, 1.06152 …

We can rephrase these numbers using the following notation:

2⁰, 2¹, 2², 2³, 2⁴, 2⁵, 2⁶ …

3⁰, 3¹, 3², 3³, 3⁴, 3⁵, 3⁶ …

1.01⁰, 1.01¹, 1.01², 1.01³, 1.01⁴, 1.01⁵, 1.01⁶ …

The small number at the top right of the normal-sized number is called the ‘exponent’, or power, and it denotes the number of times you must multiply the normal-sized number by itself. Sequences that increase proportionately display ‘exponential’ growth – since for each new term the exponent increases by one.

When a number grows exponentially, the bigger it gets the faster it grows, and after only a handful of repetitions the number can reach a mind-boggling size. Consider what happens to a sheet of paper as you fold it. Each fold doubles the thickness. Since paper is about 0.1mm thick, the thickness in millimetres after each fold is

0.1, 0.2, 0.4, 0.8, 1.6, 3.2, 6.4 …

which is the doubling sequence we saw above, but with the decimal point one place along. Because the paper is getting thicker, each successive fold requires more strength, and by the seventh it is physically impossible to fold any further. The paper’s thickness at this point is 128 times that of the single sheet, making it as thick as a 256-page book.

But let’s carry on, to see – theoretically at least – how thick the piece of paper will get. After six more folds the paper is almost a metre tall. Six folds after that it is the height of the Arc de Triomphe, and six folds after that it towers 3km into the sky. Ordinary though doubling is, when we apply the procedure repeatedly, it does not take long for the results to be extraordinary. Our paper passes the Moon after 42 folds, and the total number required for it to reach the edge of the observable universe is just 92.

Albert Bartlett is less interested in other planets than the one we live on, and in his lecture he introduced a brilliantly compelling analogy for exponential growth. Imagine a bottle containing bacteria whose numbers double every minute. At 11am the bottle has one bacterium in it and an hour later, at noon, the bottle is full. Working backwards, the bottle must be half full at 11.59am, a quarter full at 11.58am, and so on. ‘If you were an average bacterium in that bottle,’ Bartlett asks, ‘at what time would you realize you are running out of space?’ At 11.55am the bottle looks pretty empty – it is only or about 3 per cent full, leaving 97 per cent free for expansion. Would the bacteria realize that they were only five minutes from full capacity? Bartlett’s bottle is a cautionary tale about the Earth. If a population is growing exponentially, it will run out of space much sooner than it thinks.

Take the history of Boulder. Between 1950, the year Bartlett moved there, and 1970, the city’s population rose by an average of six per cent a year. That’s equivalent to multiplying the initial population by 1.06 to get the population at the end of year 1, multiplying the initial population by (1.06)² to get the population at the end of year 2, multiplying the initial population by (1.06)³ to get the population at the end of year 3, and so on, which is clearly an exponential progression.

Six per cent a year doesn’t sound that much on its own, but after two decades it represents more than a tripling of the population, from 20,000 to 67,000. ‘That is just a staggering amount,’ said Bartlett, ‘and we have been fighting ever since to try and slow it down’ (it is now almost 100,000). Bartlett’s passion for explaining exponential growth came from a determination to preserve the quality of life in his mountainside hometown.

It is important to remember that whenever the percentage increase per unit of time is constant, growth is exponential, which means that even though the quantity under discussion may start growing slowly, growth will soon speed up and before long the quantity will be counter-intuitively huge. Since almost all economic, financial and political measures of growth – of sales, profits, stock prices, GDP and population, for example, as well as inflation and interest rates – are calculated as a percentage change per unit of time, exponential growth is crucial to understanding the world.

Which was also true half a millennium ago, when concern about exponential growth led to the widespread use of an arithmetical rule of thumb: the Rule of 72, first mentioned in Luca Pacioli’s Summa de Arithmetica, the mathematical bible of the Renaissance. If a quantity is growing exponentially then there is a fixed period in which it doubles, known as the ‘doubling time’. The Rule of 72 states that a quantity growing at X per cent every time period will double in size in roughly periods. (I explain how this is worked out in Appendix Five). So, if a population is growing at 1 percent a year it will take about , or 72 years, for the population to double. If the town is growing at two per cent a year it will take , or about 36 years, and if it is growing at six per cent, as it was in Boulder, it will take , or 12 years.

Doubling time is a useful concept because it allows us to see easily into the future and the past. If Boulder’s population doubles in 12 years, it will quadruple in 24 years, and after 36 years it will be eight times as big. (Providing the growth rate stays the same, of course.) Likewise, if we think about previous growth, a quantity growing at six per cent a year would have had half its current value 12 years ago, a quarter of its current value 24 years ago, and 36 years ago it would have been an eighth of the size.

By converting a percentage to a doubling time you get a better feel for how fast the quantity is accelerating, which makes the Rule of 72 indispensable when thinking about exponential growth. I remember my father explaining it to me when I was young, and he was taught it by his father, who as a clothes trader in the East End of London before the era of calculators would have relied on it in his working life. If you borrow money at 10 per cent annual interest, the rule tells you with little mental effort that the debt will double in about seven years, and quadruple in fourteen.

Albert Bartlett’s interest in exponentials soon grew beyond issues of overcrowding, pollution and traffic congestion in Boulder, since the same arguments he made to the city council applied equally to the world as a whole. The Earth cannot sustain a global population that is growing proportionately every year, or not for much longer anyway. How many minutes left are there, he asked, before the bacteria fill the bottle? Bartlett’s views have made him a modern-day Thomas Malthus, the English cleric who two hundred years ago argued that population growth leads to famine and disease, since the exponential growth of people cannot be matched by a corresponding growth in food production. ‘Malthus was right!’ Bartlett said. ‘He didn’t anticipate petroleum and mechanization, but his ideas were right. He understood exponential growth versus linear growth. The population has a capability of growing more rapidly than we can grow any of the resources we need to survive.’ And he added: ‘No matter what assumptions you make, the population crashes in the middle of this century, about 40 years from now.’

Bartlett is a gripping lecturer. He cleverly converts the vertigo you feel when considering exponential growth into the fear of an imminent, apocalyptic future. His talk is also refreshing in the way he brings the tools of physics – distilling the essence of the problem, isolating the universal law – to a discussion usually dominated by economists and social scientists. He reserves much of his ire for economists, whom he blames for a collective denial. ‘They have built up a society in which you have to have population growth to have job growth. But growth never pays for itself, and leads to disaster ultimately.’ The only viable option, he said, is for society to break its addiction to exponentials.

Opponents of Bartlett’s view argue that science will come up with solutions to increase production of food and energy, as it has managed to until now, and that birth rates are reducing globally anyway. They miss the point, he said. ‘A common response by economists has been that I don’t understand the problem, that it is more complex than this simple-minded thing. I reply that if you don’t understand the simple aspects, you can’t hope to understand the complicated aspects!’ And then he chuckled: ‘That doesn’t get me anywhere. You can’t sustain population growth, or growth in the consumption of resources, period. End of argument. It isn’t debatable, unless you want to debate arithmetic.’

Bartlett calls our inability to understand exponential growth the greatest shortcoming of the human race. But why do we find it so hard to comprehend? In 1980 the psychologist Gideon Keren of the Institute for Perception in the Netherlands conducted a study that attempted to see if there were any cultural differences in misperceptions of exponential growth. He asked a group of Canadians to predict the price of a piece of steak that was rising 13 per cent year on year. The subjects were told the price in 1977, 1978, 1979 and 1980, when it was $3, and they had to estimate the value it would reach 13 years later in 1993. The average guess was $7.7, about half the value of the correct answer, $14.7, which was a significant shortfall. Keren then asked the same question of a group of Israelis using their local currency, Israeli pounds, and with the 1980 price of a steak being I£25. The average guess for the price in 1993 was I£106.4, which while again an underestimate – the correct answer was I£122.4 – was much closer to the target. Keren argued that the Israelis performed better because their country was going through a period of about 100 per cent annual inflation at the time of the survey, compared to about 10 per cent in Canada. He concluded that with more experience of higher exponential growth, Israelis had become more sensitive to it, even if their estimates still undershot.

In 1973 Daniel Kahneman and Amos Tversky demonstrated that people make much lower estimates when evaluating 1 × 2 × 3 × 4 ×5 × 6 × 7 × 8 than they do for 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1, which are identical in value, showing that we are unduly influenced by the order in which we read numbers. (The median response for the rising sequence was 512, and 2250 for the descending one. In fact, both estimates were drastically short of the correct answer, 40,320.) Kahneman and Tversky’s research provides an insight into why we will always underestimate exponential growth: in any sequence we are subconsciously pulled down, or ‘anchored’, by the earliest terms, and the effect is most extreme when the sequence is ascending.

Exponential growth can be step-by-step, or continuous. In Bartlett’s bacteria-in-the-bottle analogy, one bacterium becomes two, two bacteria become four, four become eight, and so on. The population increases by whole numbers at fixed intervals. The curves in the illustration that follows, however, are growing exponentially and continuously. At every point the curve is rising at a rate proportional to its height.

When an equation is of the form y = a^x, where a is a positive number, the curve displays continuous exponential growth. The curves below are described by the equations y = 3^x, y = 2^x, and y = 1.5^x, which are the continuous curves of the tripling sequence, the doubling sequence and the sequence where each new term grows by 50 per cent. In the case of y = 2^x, for example, when the values of x are 1, 2, 3, 4, 5 …, the values of y are 2, 4, 8, 16, 32 …

Exponential curves.

On the smaller-scale graph, left, the curves look like ribbons pinned to the vertical axis at 1. On the larger scale graph, right, you can see how they all suffer similar fates – becoming close to vertical only a few units along the x axis. It doesn’t look like these curves will eventually cover the plane horizontally, although inevitably they will. If I wanted the graph on the right to show y = 3^x, where x = 30, the page would need to stretch for more than a hundred million kilometres in the vertical direction.

When a curve rises exponentially, the higher it gets the steeper it becomes. The further we travel up the curve, the faster it grows. Before we continue, however, we need to familiarize ourselves with a new concept: ‘gradient’, the mathematical measure of steepness. The gradient of a slope is should already be familiar to anyone who has driven or cycled up a mountain road. If a road rises 100m while travelling 400m horizontally, as illustrated below, then the gradient is , or , which a road sign will usually describe as 25 per cent. The definition makes intuitive sense, since it means that steeper roads have higher gradients. But we need to be careful. A road that has 100 per cent gradient is one that rises the same amount as it travels across, meaning that it rises at an angle of only 45 degrees. It is theoretically possible for a road to have a gradient of more than 100 per cent; in fact, it could have a gradient of infinity, which would be a vertical slope.

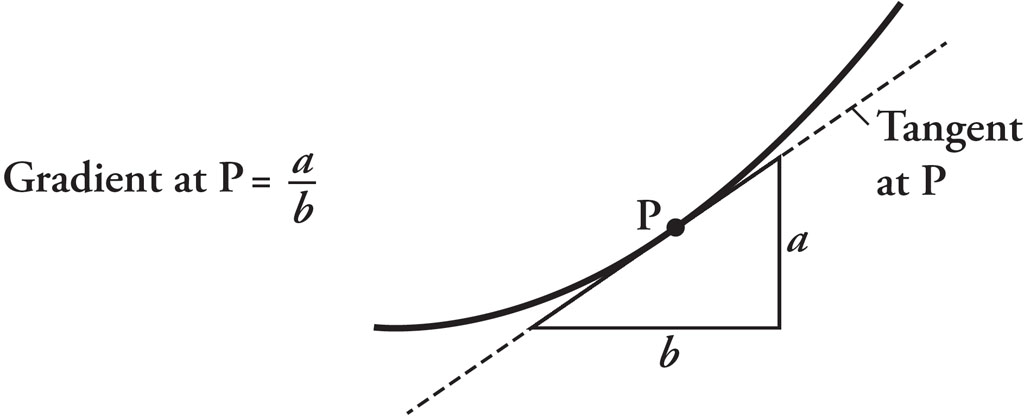
The road illustrated above has a constant gradient. Most roads, however, have a variable gradient. They get steeper, flatten out, get steeper again. To find the gradient at a point on a road, or curve, with changing steepness, we must draw the tangent at that point and find its gradient. The tangent is the line that touches the curve at that point but does not cross it (the word ‘tangent’ comes from the Latin tangere, to touch). In the illustration below of a curve with varying gradient, I have marked a point P and drawn its tangent. To find the gradient of the tangent, we draw a right-angled triangle, which tells us the height change, a, for the horizontal change, b, and then calculate . The size of the triangle doesn’t matter, because the ratio of height to width will stay the same. The gradient at point P is the gradient of the tangent at P, which is .

Let’s return to my description of exponential curves: the further we travel up them, the steeper they get. In other words, the higher up the curve you go, the higher the gradient. In fact, we can make a bolder statement. For all exponential curves, the gradient is always a fixed percentage of the height. Which leaves us with an obvious question. What is the Goldilocks curve, where the gradient and the height are always equal?

The ‘just right’ curve turns out to be:

y = (2.7182818284…)^x

When the height is 1, the gradient is 1, when the height is 2, the gradient is 2, and when the height is 3, the gradient is 3, as illustrated in the triptych below. Correspondingly, when the height is pi, the gradient is pi, and when the height is a million, the gradient is a million. As you move along the curve, its two most fundamental properties – height and gradient – are equal and rise together, an ascent of joyous synchronicity, like lovers in a Chagall painting floating up into the sky.

The curve of y = e^x: the height of a point on the curve is always equal to the gradient at that point.

The geometric beauty of the curve, however, contrasts with its ugly spawn: a splutter of decimal digits, beginning 2.718 and continuing for ever without repeating themselves. For convenience we represent this number with the letter e, and call it the ‘exponential constant’. It is the second-most-famous mathematical constant after pi. Unlike pi, however, which has been the subject of interest for millennia, e is a Johnny-come-lately.

When asked what was the greatest invention of all time, Albert Einstein is said to have quipped: ‘compound interest’. The exchange probably never took place, but it has entered urban mythology because it is just the type of playful answer we like to think he would have made. Interest is the fee you pay for borrowing money or what you receive for lending it. It’s usually a percentage of the money borrowed or lent. Simple interest is money paid on the original amount, and it stays the same each instalment. So if a bank charges 20 per cent annual simple interest on a loan of £100, then after one year the debt is £120, after two years it is £140, after three years it is £160, and so on. With compound interest, however, each payment is a proportion of the compounded, or accumulated, total. So, if a bank charges 20 per cent annual compound interest, a £100 debt will become £120 after a year, £144 after two, and £172.80 after three, because:

And so on.

Compound interest grows much faster than simple interest because it grows exponentially. Adding X per cent to a debt is equivalent to multiplying it by (1 + ), so the calculation above is equally:

Which is a sequence growing exponentially.

Moneylenders have preferred compound over simple interest for as long as we know. Indeed, one of the earliest problems in mathematical literature, on a Mesopotamian clay tablet dating from 1700 BCE, asks how long it will take a sum to double if the interest is compounded at 20 per cent a year. One reason why banking is so lucrative is that compound interest increases the debt, or loan, exponentially, meaning that you can end up paying, or earning, exorbitant amounts in a short time. The Romans condemned compounding as the worst form of usury. In the Koran it is decreed sinful. Nevertheless, the modern global financial system relies on the practice. It’s how our bank balances, credit card bills and mortgage payments are calculated. Compound interest has been the chief catalyst of economic growth since civilization began.

In the late seventeenth century the Swiss mathematician Jakob Bernoulli asked a pretty basic question about compound interest. In what way does the compounding interval matter to the value of a loan? (Jakob was the elder brother of Johann, who we met last chapter challenging the world’s most brilliant mathematicians to find the path of quickest descent.) Is it better to be paid the full interest rate once a year, or half the annual rate compounded every half a year, or a twelfth the annual rate compounded every month, or even the annual rate compounded every day? Intuitively, it would seem that the more we compound the more we stand to make, which is indeed the case, since the money spends more time ‘working’ for us. I will take you through the calculation step by step, however, since it throws up an interesting arithmetical pattern.

To keep the numbers as simple as possible, let’s say our deposit is £1 and the bank pays an interest rate of 100 per cent per annum. After one year, the value of the deposit will double to £2.

If we halve the interest rate and the compounding interval, we get a 50 per cent rate to be compounded twice.

After six months our deposit will grow to:

And after a year it will be:

So, by compounding every six months, we make an extra 25p.

Likewise, if the interest rate is a 12th of 100 per cent and there are twelve monthly payments, the deposit will grow to:

By compounding monthly, we make an extra 61p.

And if the interest rate is a 365th of 100 per cent, and there are 365 daily payments, the deposit will grow to:

We make an extra 71p.

The pattern is clear. The more compounding intervals there are, the more our money earns. Yet how far can we push it? Jakob Bernoulli wanted to know if there were any limits to how high the sum could grow if the compounding intervals continued to divide into smaller and smaller time periods.

As we have seen, if we divide the annual percentage rate by n and compound it n times, the end-of-year balance in pounds is:

Rephrasing Bernoulli’s question algebraically, he was asking what happens to this term as n approaches infinity. Does it also increase to infinity or does it approach a finite limit? I like to visualize this problem as a tug of war along the horizontal axis of a graph. As n gets bigger, gets smaller, pulling the term to the left. On the other hand, the exponent ⁿ is pulling the term to the right, since the more times you multiply what’s in the brackets the larger the sum will be. At the start of the race the exponent is winning, since we have seen that when n is 1, 2, 12 and 365 the value of grows, from 2 to 2.25 to 2.6130 to 2.7146. You can probably see where we’re going. When n heads to infinity, the tug-of-war reaches equilibrium. Bernoulli had unintentionally stumbled on the exponential constant, since in the limit, when n tends to infinity, tends to e.

Let’s look at this process visually. The illustration below contains three scenarios of what happens to a deposit of £1 over a year with a 100 per cent per annum interest rate, compounded proportionally at different intervals. The dashed line represents biannual compounding, and the thin line monthly compounding. With more steps, the lines rise higher. When the steps are infinitely small, the line is the curve y = e^x, the poster boy of exponential growth.

The value of £1 over a year when a 100 per cent annual interest rate is compounded biannually, monthly and continuously.

We say that the curve is ‘continuously compounding’, meaning that the value of our deposit is growing at every instant throughout the year. At the end of one year, the balance is £2.718…, or £e.

Bernoulli discovered e while studying compound interest. He would no doubt be delighted to discover that his foundling is the bedrock of modern banking (with more realistic interest rates, obviously). This is because British financial institutions are legally obliged to state the continuously compounded interest rate on every product they sell, irrespective of whether they choose to pay monthly, biannually, annually, or whatever.

Let’s say that a bank offers a deposit account that pays 15 per cent per annum, compounded in one annual instalment, which means that after one year a £100 loan will grow to £115. If this 15 per cent is compounded continuously, a formula derived from the properties of e tells us that after one year the loan will grow to £100 × e^15/100, which works out at £116.18, or an annual interest rate of 16.18 per cent. The bank is required by law to declare that this particular deposit account pays 16.18 per cent. While it seems odd for banks to declare a figure they don’t use in practice, the rule was introduced so that customers could compare like with like. An account that pays monthly and one that pays annually are both judged by their continuously compounded rates. Since almost every financial product involves compound interest, and every calculation of continuous compounding throws up an e, the exponential constant is the pivotal number on which the entire financial system depends.

That’s enough about money. Many other phenomena exhibit exponential growth, such as the spread of disease, the proliferation of microorganisms, the escalation of a nuclear chain reaction, the expansion of internet traffic and the feedback of an electric guitar. In all these cases, scientists model the growth using e.

I wrote previously that the equation y = a^x, where a is a positive number, describes an exponential curve. We can rephrase this equation so it has an e in it. The arithmetic of exponents means that the term a^x is equivalent to the term e^kx for a unique, positive number k. For example, the curve of the doubling sequence has the equation y = 2^x, but it can also be written y = e^0.693x. Likewise, the curve of the tripling sequence, y = 3^x, has the equivalent form y = e^1.099x. Mathematicians prefer to convert the equation y = a^x into an equation y = e^kx because e represents growth in its purest form. It simplifies the equation, facilitates calculation and is more elegant. The exponential constant e is the essential element of the mathematics of growth.

Pi is the first constant we learn at school, and only those who specialize in maths will later learn e. Yet at university level, e predominates. Even though it is purely coincidental that e is also the most common letter in the English language, the mathematical role of e actually has a parallel to its linguistic one. When an equation has an e in it, it indicates a bud of exponential growth, a flowering, a sign of life. Correspondingly, an e brings vitality to written language, trans-forming contiguous consonants into pronounceable words.

Exponential growth has an opposite: exponential decay, in which a quantity decreases repeatedly by the same proportion.

For example, the halving sequence:

exhibits exponential decay.

The equivalent concept of ‘doubling time’ for exponential decay is ‘half-life’, the fixed length of time it takes for a quantity to decrease by half. It’s a common term in nuclear physics, for example. The number of radioactive particles in a radioactive material decays exponentially, and with enormous variation too: the half-life of hydrogen-7 is 0.000000000000000000000023 seconds, while for calcium-48 it is 40,000,000,000,000,000,000 years.

More mundanely, the difference in temperature between hot tea and the mug you have just poured it into decays exponentially, as does the atmospheric pressure as you walk up a hill.

The purest curve of exponential decay is y = , which is also written y = e^–x, illustrated below, for which the gradient is always the negative of the height. The decay curve is just the exponential curve y = e^x reflected in the vertical axis. One interesting property of this curve is that the (shaded) region bounded by the curve, the vertical axis and the horizontal axis has finite area, equal to 1, even though the area is infinitely long, since the curve never reaches the horizontal axis.

The curve of exponential decay.

In the May 1690 issue of the Acta Eruditorum, Jakob Bernoulli, the discoverer of e, revisited a question that had been puzzling mathematicians for a century. What is the correct geometry of the shape made by a piece of string when it is hanging between two points? This curve – called the ‘catenary’, from the Latin catena, chain – is produced when a material is suspended by its own weight, as shown below. It’s the sag of an electricity cable, the smile of a necklace, the U of a skipping rope and the droop of a velvet cord. The cross section of a billowing sail is also a catenary, rotated by 90 degrees, since wind acts horizontally as gravity does vertically. In a departure from many of the other mathematical challenges posed in the seventeenth century, however, Jakob did not know the answer to his question before he asked it. After a year’s work it still eluded him. His younger brother Johann eventually found a solution, which you might assume would be a cause for great joy in the Bernoulli household. It wasn’t. The Bernoullis were the most dysfunctional family in the history of mathematics.

Maths bling: the catenary curve.

Originally from Antwerp, the Bernoullis had fled the Spanish persecution of the Huguenots, and by the early seventeenth century were spice merchants settled in Basel, Switzerland. Jakob, born in 1654, was the first mathematician of what was to become a family dynasty unmatched in any field. Over three generations, eight Bernoullis would become distinguished mathematicians, each with significant discoveries to their names. Jakob, as well as studying compound interest, is perhaps best known for writing the first major work on probability. He was also ‘self-willed, obstinate, aggressive, vindictive, beset by feelings of inferiority and yet firmly convinced of his own abilities’, according to one historian. This set him on a collision course with Johann, thirteen years his junior, who was similarly disposed. Johann relished solving the catenary problem, and later recounted the episode with glee: ‘The efforts of my brother were without success; for my part, I was more fortunate, for I found the skill (I say it without boasting, why should I conceal the truth?) to solve it in full,’ he wrote, adding: ‘It is true that it cost me study that robbed me of rest for an entire night …’ One entire night for a problem his brother failed to solve in a year? Ouch! Johann was as competitive with his sons as he was with his brother. After he and his middle son Daniel were awarded a shared prize from the Paris Academy, he was so jealous he barred Daniel from the family home.

The curve whose identity Jakob Bernoulli so ardently sought turned out to have a hidden ingredient, e, the number he had uncovered in a different context.

In modern notation, the equation for the catenary is:

where a is a constant that changes the scale of the curve. The bigger a is, the further apart the two ends of the hanging string are, as illustrated below.

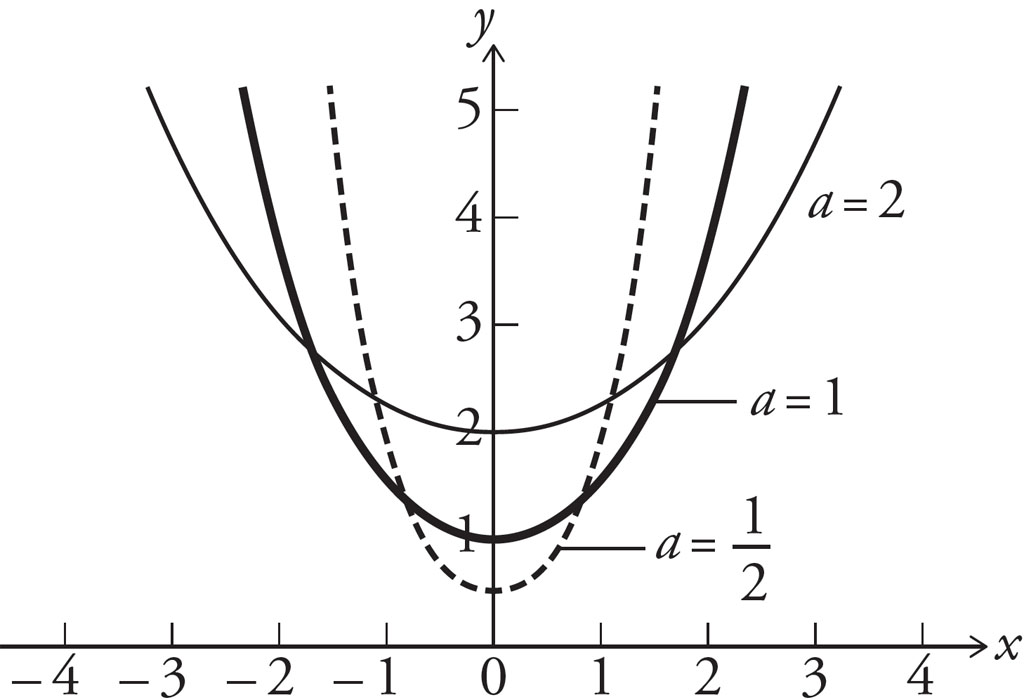
The catenary equation with different values for a.

If we let a = 1 in the catenary equation, then the curve is

Look closely at the equation. The term e^x represents pure exponential growth, and the term e^–x pure exponential decay. The equation adds them together, and then divides by two, which is a familiar arithmetical operation; adding two values and halving the result is what we do when we want to find their average. In other words, the catenary is the average of the curves of exponential growth and decay, as illustrated below. Every point on the U falls exactly halfway between the two exponential curves.

The catenary is the average of exponential growth and decay.

Whenever we see a circle, we see pi, the ratio of the circumference to the diameter. And whenever we see a hanging chain, a dangling spider’s thread or the dip of an empty washing line, we see e.

In the seventeenth century, the English physicist Robert Hooke discovered an extraordinary mechanical property of the catenary: the curve, when upside down, is the most stable shape for a free-standing arch. When a chain hangs, it settles in a position where all its internal forces are pulling along the line of the curve. When the catenary is turned upside down, these forces of tension become forces of compression, making the catenary the unique arch where all compression forces are acting along the line of the curve. There are no bending forces in a catenary: it supports itself under its own weight, needing no braces or buttresses. It will stand sturdily with a minimal amount of masonry. Bricks in a catenary will not even need mortar to stand stable, since they push against each other perfectly along the curve. Hooke was pleased with his discovery, declaring it an idea that ‘no Architectonik Writer hath ever yet attempted, much less performed’. It was not long, however, before engineers were using catenaries. Before the computer age the quickest way to make one was to hang a chain, trace out the curve, build a model using a rigid material and stand it upside down.

The catenary is nature’s legs, the most perfect way to stand on two feet. The arch, in fact, was a signature motif of Antoni Gaudí, the Catalan architect responsible for some of the most stunning buildings of the early twentieth century, notably the basilica of the Sagrada Família in Barcelona. Gaudí was drawn not just to the aesthetics of the catenary but also to what it represented mathematically. His use of catenaries made the structural mechanics of a building a principal feature of its design.

Arches in buildings, however, are rarely free-standing. Usually they form columns or vaults linked to walls, floors and the roof. Gaudí realized that the entire architecture of a building could be drafted using a model of hanging chains, and this is just what he did. For example, when he was commissioned to design a church at the Colònia Güell near Barcelona, he made an upside-down skeleton of the project. Instead of using metal chains, he used string weighed down by hundreds of sachets containing lead shot. The weight of each sachet on the string created a mesh of ‘transformed’ catenary curves. The arches of these transformed catenaries were the most stable curves to withstand a corresponding weight at the same position (such as the roof, or building materials). To see what the finished church would look like, Gaudí took a photograph and turned it upside down. Even though the Colònia Güell Church was never finished, it inspired him to use the same technique in his later work.

A replica of a Gaudí chain model hanging in the Pedrera-Casa Milà museum in Barcelona. Turn the image upside down to see the shape of the intended building.

The most famous catenary is probably the Gateway Arch in St Louis, Missouri, which is 192m high, although it is slightly flatter than a perfect curve to take account of thinner masonry at the top. In 2011 London architects Foster and Partners decided on the catenary for a particularly challenging project: a mega-airport in Kuwait, one of the most inhospitable but inhabited places on Earth. Nikolai Malsch, the lead architect on the project, explained to me that the best shape for the roof of the 1.2km-long building was a shell with a catenary cross-section. Even though the catenary would be gigantic – 45m wide at the base and 39m high in the middle – the efficiency with which it would distribute its own weight meant that it only needed to be 16cm thick. ‘A non-catenary curve might be perfectly doable, but it takes more material, it has bigger beam sections, and overall it is much more complicated to construct,’ he said. ‘Even if the cladding falls out, the interiors and everything else falls away and the whole thing turns to dust and rubble and sand, [the catenary] should still stand.’

The office of Foster and Partners contains detailed models of its most famous projects: London’s ‘Gherkin’ tower, the Reichstag in Berlin and the suspension bridge at Millau, France. Yet on the table in front of Nikolai Malsch was a hanging bicycle chain. ‘We love the catenary,’ he said, ‘because it tells the story of holding up the roof.’

The catenary has another, less widely known role in architecture, unlikely to feature in the design of churches and airports. A track of upside-down catenary humps is the required surface for the smooth riding of a square-wheeled bicycle, or for a bowling alley with cube-shaped balls.

Mathematician Stan Wagon rides his trike at Macalester College, St Paul, Minnesota.

 

Even though the Bernoullis produced more significant mathematicians than any other family in history, the greatest mathematician to emerge from Basel during their lifetimes wasn’t one of them. Leonhard Euler (pronounced OIL-er) was the precociously clever son of a local pastor, with mathematical gifts that were first discovered, and then nurtured, by Johann Bernoulli, his Sunday-afternoon tutor. When he was 19, in 1727, Euler emigrated to Russia to take up a position at the newly opened Saint Petersburg Academy of Sciences, where Johann’s son Daniel held the chair of mathematics. Peter the Great was offering royal salaries to lure over the brightest European minds, and Saint Petersburg provided a much more stimulating and high-profile intellectual environment than Basel. Euler was soon its most celebrated scholar.

Euler was a tranquil, devoted family man quite unlike the cliché of the socially awkward mathematical genius. His quirks were a prodigious memory – it is said he could recall all ten thousand lines of Virgil’s Aeneid – and an even more prodigious work rate. No mathematician has come close to equalling his output, which averaged about 800 pages a year. When he died aged 76, in 1783, so much was left on his desk that his articles continued to appear in journals for another half century. Euler struggled with poor sight all his life, losing the use of his right eye in his late twenties and his left in his mid-sixties. He dictated some of his most important work while blind, to a roomful of scribes who scrambled to keep up. He could create mathematics, they said, faster than you could write it down.

But it wasn’t just the quantity of his research that makes Euler stand out. It was also the quality and the diversity. ‘Read Euler, read Euler,’ implored the French mathematician Pierre-Simon Laplace. ‘He is the master of us all.’ Euler made important contributions to almost every field at the time, from number theory to mechanics, and from geometry to probability, as well as inventing new ones, too. His work was so transformational that the maths community adopted his symbolic vocabulary. Euler is the reason, for example, that we use π and e for the circle and exponential constants. He was not the first person to write π – that was a little-known Welsh mathematician, William Jones – but it was only because Euler employed the symbol that it gained widespread use. He was, however, the first person to use the letter e for the exponential constant, in a manuscript about the ballistics of cannonballs. The assumption is that he chose e because it was the first ‘unused’ letter available – mathematical texts were already full of a’s, b’s, c’s and d’s – rather than naming it after the word ‘exponential’ or his own surname. Despite his successes, he remained a modest man.

Euler made an unexpected discovery about e, which I will come to once I introduce a new symbol, the exclamation mark (which was not one of Euler’s coinages). When a ‘!’ is written immediately after a whole number it means that the number must be multiplied by all the whole numbers smaller than it. The ‘!’ operation is called the ‘factorial’, so the number n! is read ‘n-factorial’.

The factorials begin:

(0! = 1 by convention)

1! = 1

2! = 2 × 1 = 2

3! = 3 × 2 × 1 = 6

4! = 4 × 3 × 2 × 1 = 24

…

10! = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 3,628,800

…

Factorials grow fast. By the time we get to 20! the value is in the quintillions. The decision by German mathematicians in the nineteenth century to adopt the exclamation mark was possibly a comment on this phenomenal acceleration. Some English texts from that time even suggested that n! should be read ‘n-admiration’ rather than ‘n-factorial’. Certainly, one can only admire the upwards trajectory of the exclamation mark: factorial outpaces even exponential growth.

Factorials appear most frequently when calculating combinations and permutations. For example, how many ways can you sit a certain number of people on the same number of chairs? Trivially, a single person can sit on a single chair in just one way. With two people and two chairs, there are two choices, the permutations AB and BA. With three people and three chairs there are six ways: ABC, ACB, BAC, BCA, CAB and CBA. Rather than listing all the permutations, however, there is a general method to find the total. The first sitter has three choices of chair, the second sitter has two and the third has one, so the total is 3 × 2 × 1 = 6. Adopting the same method with four people and four chairs, we find that the total is 4 × 3 × 2 × 1 = 4! = 24. In other words, if you have n people and n chairs the number of permutations is n! It is striking to realize that if you have a dinner party for ten people, you can fit them around a table in more than three and a half million ways.

Now let’s return to e. The exponential constant can be written with a whole bunch of exclamation marks. OMG!!! LOL!!! It turns out that if we calculate for every number starting from 0, then add up all the terms, the answer is e.

 

Written as an equation:

Which is:

Let’s start counting term by term.

The series bears down on the true value of e with supersonic speed. After only ten terms it is accurate to six decimal places, which is good enough for almost any scientific application.

Why is e so beautifully expressed using factorials? As we saw with compound interest, the number is the limit of as n approaches infinity. I will spare you the details of the proof, but the term can be expanded into a giant sum that reduces into unit fractions with factorials in their denominators.

Euler’s approach to research was playful, and he often investigated frivolous games and puzzles. When a chess enthusiast asked him, for example, whether it was possible for a knight to move across the board so it would land on every square only once before returning to its point of departure, Euler discovered how to do it, presaging similar questions still researched today. Euler also became intrigued by the French card game jeu de rencontre, or the game of coincidence, a variation of one of my favourite pastimes as a child, Snap!

In rencontre, two players A and B have a shuffled deck of cards each. They both turn over a card from their respective packs at the same time, and continue revealing cards simultaneously until all are used up. If at any turn the two cards are identical, then A wins. (And I shout ‘Snap!’) If they get through the pack with no matches, then B wins. Euler wanted to know the likelihood of A winning the game; that is, of there being at least one coincidence in 52 turns.

This question has reappeared in many guises over the years. Imagine, for example, that a cloakroom attendant fails to tag any of the items that are handed in over an evening, and gives them back randomly to guests at the end of the night. What is the chance that at least one person receives the right coat back? Or say that a cinema sells numbered tickets but then lets members of the audience sit wherever they like. If the theatre is full, what is the chance that at least one seat is occupied by a person with the correct ticket?

Euler started at the beginning. When the rencontre pack given to each player consists of one card, there is a 100 per cent chance of a match. When the pack consists of two cards, there is a 50 per cent chance. Euler drew permutation tables for games played with three-card and four-card packs before deducing the pattern. The probability of a match when there are n cards in the pack is the fraction:

Hang on! This pattern looks similar to the series for e above.

I’ll skip the guts of the proof, but this series approximates to , or about 0.63. The series is only exactly when n gets to infinity, but the approximation is already very, very good after a few terms. When n = 52, the number of cards in a pack, the series is correct to almost 70 decimal places.

The chance of a coincidence in eu de rencontre, therefore, is about 63 per cent. It’s roughly twice as likely to happen as it is not. Likewise, the chance of at least one party guest getting his coat back is 63 per cent, and the chance of a cinema-goer sitting on the correct seat is also 63 per cent. It is interesting to note that the number of cards in the deck, guests handing in coats, or seats in the cinema makes little difference to the chances of at least one match, provided there are more than six or seven cards, guests or seats. Each time you increase the number of cards, guests or seats, you add an extra term in the series above that determines the probability of a match. An eighth card, for example, gives you an eighth term, , or 0.0000248, which alters the probability by less than a quarter of a hundredth of one per cent. A ninth card alters the probability by even less. In other words, the chances of a match barely change whether you’re playing with a full deck or just the cards of one suit. Similarly, it makes almost no difference whether ten or a hundred guests check their coats, or if the cinema is the smallest screen in your local multiplex or the Empire Leicester Square.

Euler’s discovery that e is embedded in the maths of card games is one of the earliest instances of the constant appearing in an area with no obvious connection to exponential growth. It would later appear in an equally competitive arena: the maths of finding a wife.

Let’s briefly return to Johannes Kepler. After the German astronomer was widowed in 1611, he interviewed eleven women for the position of the second Frau K. The task started badly, he wrote: the first candidate had ‘stinking breath’, the second ‘had been brought up in luxury that was above her station’, and the third was engaged to a man who had sired a child with a prostitute. He would have married the fourth, of ‘tall stature and athletic build’ had he not seen the fifth, who promised to be ‘modest, thrifty, diligent and to love her step-children’. But his prevaricating caused both women to lose interest and he saw a sixth, whom he ruled out because he ‘feared the expense of a sumptuous wedding’, and a seventh, who, despite her ‘appearance which deserved to be loved’, rejected him when he again did not decide quickly enough. The eighth ‘had nothing to recommend her, [even though] her mother was a most worthy person’, the ninth had lung disease, the tenth had a ‘shape ugly even for a man of simple tastes … short and fat, and coming from a family distinguished by redundant obesity’, and the final candidate was not grown-up enough. At the end of the process Kepler asked: ‘Was it Divine Providence or my own moral guilt which, for two years or longer, tore me in so many different directions and made me consider the possibilities of such different unions?’ Such agonized self-searching is familiar in the modern dating scene. What the great German astronomer needed was a strategy.

Consider the following game, which, according to the maths author Martin Gardner, was invented by a couple of friends, John H. Fox and L. Gerald Marnie, in 1958. Ask someone to take as many pieces of paper as they like, and to write a different positive number on each one. The numbers can be anything from a tiny fraction to something absurdly enormous, say 1 with a hundred zeros after it. The pieces of paper are placed face down on a table and shuffled around. Now the game begins. You turn over the pieces of paper one by one. The aim is to stop when you turn over the paper with the largest number on it. You are not allowed to go back and pick a number on a paper that you have already turned. And if you keep on going and turn over all the papers, your pick is the last one you turned.

Since the player turning over the papers has no idea of the numbers written on them, you might think that his or her chances of picking the highest number are slim. Astoundingly, however, it is possible to win this game more than a third of the time, irrespective of how many pieces of paper are being used. The trick is to use information from numbers you have already seen to make a judgement about the numbers that remain face down. The strategy: turn over a certain quantity of the slips, benchmark the highest number among this selection, and then pick the first number you turn over that is higher than the benchmark. The optimal solution, in fact, is to turn over (or 0.368, or 36.8 per cent) of the total number of pieces of paper and then to choose the first number higher than any number in that selection. If you do, the chance of picking the highest number is again , or 36.8 per cent.

In the 1960s this conundrum became known as the Secretary Problem, or the Marriage Problem, as it was analogous to the situation of a boss looking at a list of applicants, or a man looking at a list of potential wives, and having to decide how to choose the best candidate. (And evidently because mathematicians were mainly men.)

Imagine you are interviewing twenty people to be your secretary, with the rule that you must decide at the end of each interview whether or not to give that applicant the job. If you offer the job to the first candidate, you cannot see any of the others, and if you haven’t chosen anyone by the time you see the last candidate you must offer the job to her. Or imagine you have decided to date twenty women, with the proviso that you must decide whether she is The One before moving on to the next. (Apologies to female readers. The analogy is based on the notion that it’s men who propose to women, and that, once proposed to, a woman will always say yes.) If you propose on the first date, you are not allowed to meet any of the others, but if you date them all you must propose to the final one you see. In both cases the way to maximise your chances of choosing the best match is to interview or date 36.8 per cent of the candidates and then offer the job or propose to the next candidate better than all those who came before. The method will not guarantee that you find the best match – the chances are only 36.8 per cent – but it is still the best strategy overall.

If Kepler had realized he was going to interview eleven women, and had followed this strategy, he would have interviewed 36.8 per cent of them, which works out as four, and then proposed to the next one he liked more than any of those. In other words, he would have chosen the fifth, which is what he did indeed do once he had seen all eleven (it turned out to be a happy marriage). Had he known the Marriage Problem and its solution, Kepler would have saved himself six bad dates.

The Secretary/Marriage Problem has become one of the most famous questions in recreational mathematics, even though it does not reflect reality, since bosses can recall candidates and men can return (as Kepler did) to previous dates. Underlying the whimsy, however, is a whole field of incredibly useful theory, called ‘optimal stopping’, or the maths of when is the best time to stop. Optimal stopping is important in finance, for working out when it’s time to cut one’s losses on an investment, or when to exercise a stock option. But it also comes into areas as diverse as medicine (to, say, calculate the best time to stop a particular treatment); economics (to project when is the best time to stop relying on fossil fuels, for example); and zoology (deciding, say, when is the best time to stop searching a large population of animals for new species, and so avoid wasting money looking for what probably isn’t there).

Boris Berezovsky, the billionaire Russian oligarch, used to be a maths professor at the USSR Academy of Sciences, the Soviet descendent of Euler’s alma mater. While there in the 1980s, he co-authored a book on the Secretary Problem. He moved to the United Kingdom in 2003. I approached him for an interview several times, but each time we spoke he asked me to call back in a couple of months. After a year of trying, I figured it was optimal to stop.

The point about optimal stopping is that it is possible to make informed decisions about random events based on accumulated knowledge. Here is a game with a fantastically ingenious way of making use of the tiniest amount of information (it does not concern e, but please forgive me for this brief detour from exponentials). The result is so bafflingly counterintuitive that when it first did the rounds, many mathematicians did not believe it.

The game is simple. You write down two different numbers on separate pieces of paper and then place them both face down. I will turn over one of the numbers and tell you whether or not it is bigger than the one that remains hidden. Amazing though it seems, I will get the answer right more than half the time.

My performance sounds like magic but there is no trick. Nor does my strategy rely on the human element of how you selected the numbers, or how you placed the paper on the table. Mathematics, not psychology, provides me with a method to win more times than I lose.

Just say that I am not allowed to turn over any of the pieces of paper. The odds of guessing which one has the highest number on it are 50/50. There are two choices, and one will be correct. My chances of getting the right answer are the same as flipping a coin.

But when I see one of the numbers, however, my odds will improve if I take the following steps:

(1) I generate a random number myself – let’s call it k.

 

(2) If k is less than the number I turned over, I say the number I turned over is highest.

 

(3) If k is more than the number I turned over, I say the number that remains face down is highest.

My strategy, in other words, is to go with the number I see, unless my random number k is larger. In this case I switch to the one I have not seen.

To see why the strategy gives me an edge, we need to consider the value of k with respect to the two numbers on the pieces of paper. There are three possibilities: (i) k is less than both of them, (ii) k is higher than both of them, or (iii) k is between them.

In the first scenario, whatever number I see, I stick with it. My chances of being right are 50/50. In the second scenario, whatever number I see, I choose the other one. My chances are again 50/50. The interesting situation is the third one, when I win 100 per cent of the time. If I see the lowest number, I switch, and if I see the highest number, I stick with it. When my random number serendipitously falls in the middle of the two numbers you wrote on the pieces of paper, I will always win!

(I need to explain in a little more detail how I generate k, since for the strategy to work k must always have a chance of being between any two given numbers. Otherwise, it is easy to find scenarios where I do not have an edge. For example, if you always write down negative numbers and my random number is always positive then my number will never be between yours and my odds of success stay at 50/50. My solution is to choose a random number from a ‘normal distribution’, since this gives a chance for all positive and negative numbers to come up. You don’t need to know anything more about normal distributions other than that they provide a way of giving a random number that has a chance of being between any two other numbers.)

There may only be a small chance that k will fall between your numbers. But because there is a chance, no matter how meagre, it means that if we play this game enough times my overall odds of winning increase beyond 50 per cent. I will never know a priori when I will win and when I will lose. But I never promised that. All I said is that I can win more than half the time. If you want to make sure that my odds stay as close to 50/50 as possible, you need to choose two numbers that are as close together as possible. Yet as long as they are not equal, there is always the chance that I will choose a number between them, and as long as this chance is mathematically possible, I will win the game more frequently than I will lose it.

Last chapter I introduced pi, which begins 3.14159 and is the number of times the diameter fits round the circumference of a circle. This chapter we got to know e, which begins 2.71828 and is the numerical essence of exponential growth. The numbers are the two most frequently used mathematical constants, and are often spoken of together, even though they emerged from different quests and have different mathematical personalities. It is curious that they are close to each other, less than 0.5 apart. In 1859 the American mathematician Benjamin Peirce introduced the symbol for pi and the symbol for e, as if to show that they are both somehow images of each other, but his confusing notation never caught on.

Both constants are irrational numbers, which means that the digits in their decimal expansions go on forever without endlessly repeating themselves. It has become something of a mathematical sport to try to find arithmetical combinations of both terms that are as elegant as possible. We are never going to find equations with absolute equality, but:

π⁴ + π⁵ = e⁶

which is correct to seven significant figures.

In a similar vein:

e^π – π = 19.999099979…

which is very, very close to 20.

And, most impressively:

= 262537412640768743.99999999999925007…

which is less than a trillionth from a whole number!

In 1730 the Scottish mathematician James Stirling discovered the following formula:

It gives an approximation for the value of n!, the factorial of n, which as we saw above is the number you get when you multiply 1 × 2 × 3 × 4 × … × n.

The factorial is a simple procedure, just multiplying whole numbers together, so it is arresting to see that on the right side of the formula there is a square root sign, a pi and an e.

When n = 10, the approximation is less than one per cent off the real value of 10!, and the bigger n gets the more accurate the approximation becomes in percentage terms. Since factorials are such huge numbers (10! is 3,628,800), the formula is gobsmacking.

Something’s going on between pi and e.

Leonhard Euler uncovered another coupling between the two constants, one even more surprising and stunning than Stirling’s formula. But before we get there we need to familiarize ourselves with another vowel that he introduced to our mathematical alphabet.

Prepare to meet i.

See Notes on Chapter 6