Energy Return on Investment

18.1 Introduction [1]

Many important earlier writers, including sociologists Leslie White and Fred Cottrell, and ecologist Howard Odum, have emphasized the importance of net energy and energy surplus as a determinant of human culture [2–4]. Human farmers or other food gatherers must have an energy profit to survive and a significant return for there to be specialists, military campaigns, and cities and substantially more for there to be today’s art, culture and other amenities. Net energy analysis is a general term for the examination of how much energy is left over from an energy-gaining process after correcting for how much of that energy (or its equivalent from some other source) is required to generate (extract, grow, or whatever) a unit of the energy in question. Net energy analysis is sometimes called, depending upon the specific procedures used, the assessment of energy surplus, energy balance, or, as we prefer, energy return on investment or EROI. To perform this analysis, we start with the more familiar monetary assessment and then develop how this relates to the energy behind economic processes. A somewhat more technical analysis is available in [5] and in our cited papers.

18.1.1 Economic Cost of Energy

In actual economies, energy comes from many sources—from the sun to run ecosystems and from imported and domestic sources of oil, coal, and natural gas, as well as hydropower and nuclear, and from renewable energy—most of that as firewood and hydroelectric but increasingly from wind and photovoltaics. Many of these energy sources are cheaper per unit energy delivered than oil, and some are considerably more expensive.

We have said many times that energy became cheap in the last century. How cheap? Such an analysis is not available for the United States, but it has been done for England going back to 1300 by Carey King. He found that the cost of the energy to run the economy (at that time meaning food for humans, fodder for animals, and wood for various things) was typically from 30 to 40 percent of GDP (◘ Fig. 4.4). Another way of looking at his data is that in past centuries about a third of all economic activity was to get the energy to run the rest of the economy. When coal was introduced to the economy, that was reduced to about 15–20 percent and with oil to about 5–10 percent. In other words, as fossil fuels were added to the economy, far less of the total economic activity was needed just to get fuel (and it was more potent fuel too), and this allowed some people to get wealthier, largely because they could appropriate the extra work that most workers could produce by means of fossil-fuel driven machinery.

../images/191833_2_En_18_Chapter/191833_2_En_18_Fig1_HTML.gif — Fig. 18.1
Proportion of GDP for energy

So let’s look at what this real ratio of the cost of energy (from all sources, weighed by their importance) is relative to its benefits:

$\mathrm{Economic}\ \mathrm{cost}\ \mathrm{of}\ \mathrm{energy}=\frac{\mathrm{Dollars}\ \mathrm{to}\ \mathrm{buy}\ \mathrm{energy}}{\mathrm{GDP}}$

By this token the relation of the proportional energy cost in dollars is similar, as we shall see, to the proportional energy cost in joules; in 2017 roughly 6 percent (1 trillion dollars) of the US GDP was spent by final demand for all kinds of energy in the US economy to produce the 17 trillion dollars’ worth of total GDP (◘ Fig. 18.1).

This percentage increased in the first half of 2008 as the price of oil exceeded $140 a barrel, and then it fell again. This pattern has been seen before. The abrupt rise in the price of energy during the “oil shocks” of the 1970s, the subsequent decline of this value from 1984 through 2000, and the increase again through mid-2008 had large impacts on discretionary spending, that is, the amount of income that people can spend on what they want vs. what they need, because the 5–10 percent change in total energy cost would come mainly out of that 25 percent or so percent of the economy. Thus we believe that changes in energy prices have very large economic impacts, a perspective supported by James Hamilton’s analysis [6]. What future energy prices will be is anyone’s guess, but even as economies crash in the late part of the first decades of the new millennium and subsequently cease growing or grow only very slowly, there is a great deal of information implying that dollar, and hence presumably energy, costs of fuels are increasing substantially, if irregularly. Our theory is that they will occur in large part due to declining EROI and that they will take a huge economic toll in the future. This chapter develops that argument.

18.2 What Is EROI?

Energy return on investment (EROI or sometimes EROEI, with the second E used to refer to the use of energy in the denominator) is the ratio of energy returned from an energy-gathering activity compared to the energy used in that process. In principle, the idea is to see how much energy society invests to get more energy. Usually the energy is either “already in society” and diverted (such as to make a drill bit) or could readily go to society but is diverted to getting more energy (such as natural gas used to pressurize a field). EROI is calculated from the following simple equation, although the devil is in the details:

$\mathrm{EROI}=\frac{\mathrm{Energy}\ \mathrm{returned}\ \mathrm{to}\ \mathrm{society}}{\mathrm{Energy}\ \mathrm{required}\ \mathrm{to}\ \mathrm{get}\ \mathrm{that}\ \mathrm{energy}}$

Since the numerator and denominator are usually assessed in the same units (an exception we treat later is when quality corrections are made), the ratio so derived is dimensionless, e.g., 20:1 which can be expressed as “twenty to one.” This implies that a particular process yields 20 joules on an investment of 1 joule (or Kcal per Kcal or barrels per barrel). EROI is usually and most precisely applied at the mine mouth, wellhead, farm gate, etc. that is at the point that it leaves the production facility. We call this more explicitly EROI_mm, and it is not to be confused with conversion efficiency, i.e., going from one form of energy to another such as upgrading petroleum in a refinery or converting coal to electricity. More explicit ratios are derived by King [7].

The authors of this book and other advocates of EROI believe that net energy analysis offers the possibility of a very useful approach for looking at the advantages and disadvantages of a given fuel while offering the possibility of looking into the future in a way that markets seem unable to do. Its advocates also believe that in time market prices must approximately reflect comprehensive EROIs, at least if appropriate corrections for quality are made and subsidies removed. Nevertheless we hasten to add that we do not believe that EROI by itself is necessarily a sufficient criterion by which judgments may be made. It is, however, the one we favor the most, especially when it indicates that one fuel has a much higher or lower EROI than others. In addition it is important to consider the present and future potential magnitude of the fuel, and how EROI might change with depletion or if the use of a fuel is expanded. An example of an EROI analysis is given as ◘ Fig. 8.7.

18.3 Relation of EROI to Monetary Cost

What is most important about energy to many people is its monetary cost. While the earliest studies of EROI were focused on its physical meaning and whether it was increasing or decreasing for particular fuels, there was always the assumption that high EROI fuels were likely to be cheaper per joule, as less effort had to go into getting them. So coal, which generally had a high EROI, was cheap, and oil much more expensive. This makes sense as it takes much less energy to dig coal out of the ground compared to operating a complex oil well. It would seem that as EROI tended to decrease over time, it was expected that eventually energy would become much more expensive. This is somewhat the case for oil but not for natural gas. King and Hall [8] found that over time the cost of particular energies increased and decreased in opposition to EROI (◘ Fig. 18.2). Prices would tend to increase when EROI was low (due in part to increased drilling rates) and the converse. But sometimes prices decline (as in 2015–17) due to supply and demand issues unrelated to EROI (► Chap. 13). Euan Mearns has developed the concept of the “EROI cliff,” where the impact of diminishing EROI is much greater as lower values are approached (◘ Fig. 18.3). The greatest concern is with declining EROI for the premium fuels of the United States and the world, which seems to be occurring although it is increasingly difficult to get the needed data. The large increases in production costs, however, imply a continuing decline in EROI for major fuels. When combined with “peak oil,” this might mean very lean times ahead for the production of our most important fuels (see review in Hall [5]).

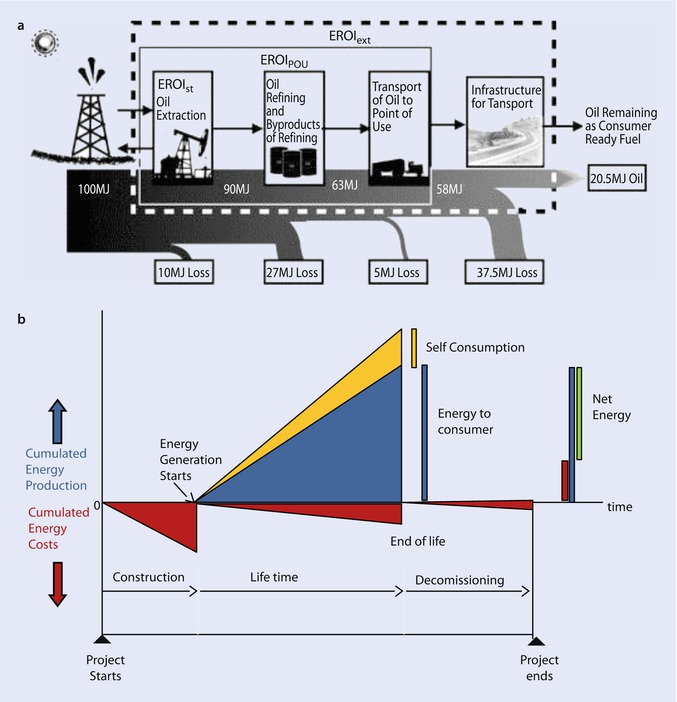
../images/191833_2_En_18_Chapter/191833_2_En_18_Fig2_HTML.jpg — Fig. 18.2
a Diagram of energy losses between the wellhead and use for petroleum (from [16]). b Schematic for the energy used and gains over time of an energy project. The EROI would be the final value of the blue triangle on top divided by the sum of the final values for the three brown triangles on bottom. These are represented by bars on right

../images/191833_2_En_18_Chapter/191833_2_En_18_Fig3_HTML.gif — Fig. 18.3
The EROI cliff. “Buffered” means including an estimate of cost of dealing with intermittency. (Courtesy Euan Mearns)

18.3.1 History

The concept of EROI was derived from Howard Odum’s teachings on net energy [2], from earlier work by anthropologists and sociologists as developed in ► Chap. 6, and explicitly from Hall’s PhD dissertation on the energy costs and gains of migrating fish [9]. The concept was implicit in Hall and Cleveland’s 1981 paper [10] on petroleum yield per effort although the term net energy was used there. The first publication using the name EROI was apparently in 1979 [11], and it received much more attention from a paper in science [12]. Somewhat detailed summaries of the literature on EROI then available were put together in a large book [13]. The concept lagged during the “energy lull” 1984–2005 but has picked up post 2005 with increasing energy prices. There are a flurry of new papers now available [e.g., 14–18]. An entire issue on EROI in the online journal Sustainability was published in 2011 with many interesting analyses [15]. Some recent controversies are developed in [5] and summarized at the end of this chapter.

There is very little quantitative information about actual EROIs for energy-producing systems for the medium or distant past, which is not surprising because we did not even understand the concept of energy until about 1850. But there is at least one example where Sundberg, mentioned in ► Chap. 6, has made a quite detailed assessment of the energy cost of energy in earlier Sweden [18]. From 1560 until 1720, Sweden was the most powerful country in Northern Europe, based mostly on its very productive metal mines but also an aggressive foreign policy backed up by high-quality weapons. The production of these mines required enormous amounts of energy for mining and especially smelting. The source of this energy was wood and especially charcoal (needed to get the high temperatures steel required) cut from Swedish forests. Ulf Sundberg gives a detailed calculation of how a typical forester and his family, self-sufficient on 2 hectares of farmland, 8 hectares of pastures, and 40 hectares of forest (collectively intercepting 1500 terrajoules of sunlight), generated some 760 gigajoules of charcoal in a year to the metal industry. To do that required about half a gigajoules of human energy or 3.5 if we include the draft animal labor. So we might calculate the EROI of the human investment to be as high as 1500:1 or some 250:1 if we include the animals. But that is just the direct energy, as it took 105 GJ to feed, warm, and support the farmer and his family (which includes his replacement) and probably at least that to support the animals. So if we include direct plus indirect energy, the EROI is down to roughly 4:1. The system was sustainable as long as the forests were not overharvested. That was true until the middle of the nineteenth century, but then the forests were severely overharvested, and many Swedes left for America.

Much of the literature on net energy in the first decade of this century tended to be about whether a given project is, or is not, a net surplus, that is, whether there is a gain or a loss in energy from, e.g., making ethanol from corn [19]. The criteria used in much of the current debate are focused on the “energy breakeven” issue, that is, whether the energy returned as fuel is greater than the energy invested in growing or otherwise obtaining it, i.e., if the EROI is greater than 1:1. The general argument seems to be that if the energy returned is greater than the energy invested, then the fuel or project “should be done,” and if not, then it should not.

Several of the participants in the current debate about corn-derived ethanol (summarized in reference [20]) argue that ethanol from corn is a clear energy surplus, with from 1.2 to 1.6 units of energy delivered for each unit invested. Further aspects of this argument center around the boundaries of the numerator, i.e., whether one should include some energy credit for nonfuel coproducts (such as residual animal feed—i.e., soybean husks or dry distiller’s grains), the quality of the fuels used and produced (e.g., liquid—presumably more valuable—vs. solid and gaseous), and the boundaries of the denominator (i.e., whether or not to include the energy required to compensate for environmental impacts in the future, e.g., for the fertilizer needed to restore soil fertility for the significant soil erosion occasioned by corn production). Such arguments are likely to be much more important in the future as other relatively low-quality fuels (e.g., oil sands or lower-quality shale oil) are increasingly considered or developed to replace conventional oil and gas, both of which are likely to be more expensive and probably less available in the not so distant future. If, of course, the alternatives require much oil and/or gas for their production, which is often the case, then an increase in the price of petroleum will not necessarily make the alternatives cheaper and more available as a fuel. We believe that for most fuels, especially alternative fuels, the energy gains are reasonably well understood, but the boundaries of the denominator, especially with respect to environmental issues, are poorly understood and even more poorly quantified. Thus we think that most calculated and published EROIs, including those we consider here, are higher (i.e., more favorable) than they would be if we had complete information. One study analyzed the reasons for differences in different studies and concluded that they were much less than usually considered [19]. The general tendency has been for recent studies to conclude that the EROI for corn-based ethanol is too close to 1:1 to conclude that they are a significant net energy source, especially if the geography of growing corn is considered [21]. Nevertheless by law 10 percent of gasoline in the United States is composed of ethanol, since the program is very popular in politically powerful corn states.

More recently there have been very strong arguments about what the EROI of solar PV is, with advocates claiming at least 10:1 and critics closer to 3:1 [22]. At this point the issue has not been resolved, although there is agreement among the analysts for procedures to bring their results much closer together [23].

18.4 Seeking an Acceptable EROI Protocol

Given the rather different quantitative responses sometimes derived from different analyses (such as the corn-based ethanol example given above), we need some good and consistent way of thinking about the meaning of the magnitude of the various EROIs of various fuels. It is our opinion that many of the EROI arguments so far are simplistic, or at least incomplete, because the “energy breakeven” point, while usually sufficient to discredit a candidate fuel, should not be the only criteria used. In addition it seems to us that many of the EROI analyses “out there” are generated from the perspective of defeating or defending a particular fuel rather than objectively assessing various potential alternatives. Perhaps we need some way to understand the magnitude, and the meaning, of the overall EROI we might eventually derive for all of a nation or society’s fuels collectively by summing all gains from fuels and all costs from obtaining them (i.e., societal EROI):

${\mathrm{EROI}}_{\mathrm{soc}}=\frac{\begin{array}{l}\mathrm{Summation}\ \mathrm{of}\ \mathrm{the}\ \mathrm{energy}\ \\ {}\mathrm{content}\ \mathrm{of}\ \mathrm{all}\ \mathrm{fuels}\ \mathrm{delivered}\end{array}}{\begin{array}{l}\mathrm{Summation}\ \mathrm{of}\ \mathrm{all}\ \mathrm{the}\ \mathrm{energy}\ \\ {}\mathrm{costs}\ \mathrm{of}\ \mathrm{getting}\ \mathrm{those}\ \mathrm{fuels}\end{array}}$

This has been undertaken for England [7] (◘ Fig. 4.7 and 8.7c). This too shows a great increase in the energy return on energy investment over a long period as coal and then oil became the chief supply of energy, with a possible recent uptick that may imply much lower energy returns as England’s coal mines and North Sea oil resources are increasingly depleted.

../images/191833_2_En_18_Chapter/191833_2_En_18_Fig4_HTML.gif — Fig. 18.4
EROI for imported oil for developing nations. (From Lambert et al. [17])

We need to ascertain EROI in a straightforward and universally accepted approach even while accommodating different approaches or philosophies. Of greatest concern are the boundaries of the analysis: should coproducts (such as hulls left from generating biodiesel from sunflower seeds that can be fed to animals, reducing energy needed to make the animal feed) or should we include the costs of the energy to support a laborer’s paycheck? Another important issue, which accounts for much of the divergence in the estimates of EROI for PV, is whether the numerator should be multiplied by three to account for the fossil energy that would have needed to be burned to generate that amount of electricity? Since there are no clear and unambiguous answers to those questions, Murphy et al. [24] have advocated a basic EROI approach—using simple standardized energy output divided by the direct (i.e., on site) and indirect (i.e., energy used off site to make the steel used on site)—to generate a standard EROI, EROI_st. This approach allows the comparison of different fuels even when the analysts do not agree on the methodology that should be used. Murphy et al. advocate the use of other supplementary EROIs, including new approaches that allow for special consideration of other aspects of that EROI at the author’s discretion. We believe this allows for both standardization and flexibility:

${\mathrm{EROI}}_{\mathrm{st}}=\frac{\mathrm{Energy}\ \mathrm{returned}\ \mathrm{to}\ \mathrm{society}}{\begin{array}{l}\mathrm{Direct}\ \mathrm{and}\ \mathrm{indirect}\ \mathrm{energy}\\ {}\mathrm{required}\ \mathrm{to}\ \mathrm{get}\ \mathrm{that}\ \mathrm{energy}\end{array}}$

18.5 The Best Analyses of the Energy Costs

Determining the energy content of the numerator of the EROI equation is usually pretty easy: multiply the quantity produced by the energy content per unit. Determining the energy content of the denominator is usually considerably more difficult. Usually one includes the energy used directly, that is, on site, and this includes the energy used to rotate the drilling bit and pressurize the field, operate the farm tractor, and so on. One usually also includes the energy used indirectly, that is, to make the drilling bit and associated materials, the tractor, and so on. Unfortunately companies generally do not keep track of their energy expenditures, but only their dollar expenditures. Forty years ago a remarkable group at the University of Illinois, including Bullard, Hannon, Herendeen [25], and Costanza [26], undertook such calculations for every sector of the US economy. Using input output analysis (who buys how much of what from other sectors) and very comprehensive energy use information, they were able to generate very detailed determinations of how much energy it took to make all products of the US economy. These allowed us at the time to gain very detailed assessments of where and how energy was used in the US economy and also the energy costs of getting energy.

These analyses also showed that (except for energy itself) it does not matter enormously where money is spent within final demand due to the complex interdependency of our economy (i.e., the final products that consumers buy are relatively unimportant to overall GDP/energy efficiency because there are so many interdependencies, i.e., each sector purchases from many other sectors within our economy, although this does not apply to the intermediate products purchased by manufacturers). According to Costanza [26], the market selects for generating a similar amount of wealth per unit of energy used within the whole economic “food chain” leading to final demand. While this is not exactly true, it is close enough for our present purposes, and it is certainly true for the average of all economic activity, with the exception of purchases for energy itself. This is because energy purchases include a similar amount of embodied energy per dollar spent as the societal mean but in addition the chemical energy of the fuel. Unfortunately there has been little such analysis of such “sector interdependencies” since these pioneering works, so that it is hard to make such assessments today. The closest assessment that is available (to our knowledge) is the analyses undertaken by various people at Carnegie Mellon University (Green energy and available on their website).

We next show how an EROI analysis can generate some quite interesting results that can help us understand the importance of EROI for running an actual economy.

18.6 How Much Energy Is Needed to “Get the Job Done”: Calculating EROI at the Point of Use

The EROI that is needed to undertake some activity, such as to drive a truck, is far more than just what is needed to get the fuel out of the ground. This was assessed in 2008 by Hall et al. [1]. In the spirit of flexibility that we introduced in several sections previously, we introduce here new concepts that start with EROI_mm, the standard EROI at the mine mouth (or farm gate, etc.), and then take it further along the use “food chain.” While technically it is probably better to calculate the EROI at the mine mouth and then look at the efficiency of using it, we can also calculate the total EROI further along its use path. We call this next step EROI at the “point of use” or EROI_pou:

${\mathrm{EROI}}_{\mathrm{pou}}=\frac{\begin{array}{c}\mathrm{Energy}\ \mathrm{returned}\ \mathrm{to}\\ {}\mathrm{society}\kern0.50em \mathrm{at}\kern0.50em \mathrm{point}\ \mathrm{of}\ \mathrm{use}\end{array}}{\begin{array}{c}\mathrm{Energy}\ \mathrm{required}\ \mathrm{to}\\ {}\mathrm{get}\kern0.50em \mathrm{and}\ \mathrm{deliver}\kern0.50em \mathrm{that}\ \mathrm{energy}\end{array}}$

As we extend the energy cost of obtaining a fuel from the wellhead toward the final consumer, the energy delivered goes down, and the energy cost of getting it to that point goes up, both reducing the EROI. This begins the analysis of what might be the minimum EROI required in society. We do this by taking the standard EROI (i.e., EROI_mm) and then including in addition in the denominator first the energy requirements to get the fuel to the point of use (i.e., EROI_pou) and then the energy required to use it to generate EROI_ext, i.e., extended EROI. As stated it might be more accurate to consider it EROI up to the wellhead and then “food chain efficiency” to the point of use, but this has not been done yet.

A more comprehensive analysis of the EROI required to drive a truck, including all the energy used in the “food chain” to do so, was undertaken by Hall, Balogh, and Murphy [1]. The costs (calculated using 2005 prices and ratios) included:

Refinery losses and costs: Oil refineries use roughly 10 percent of the energy of the fuel to refine it to the form that we use. In addition about 17 percent of the material in a barrel of crude oil ends up as other petroleum products, such as lubricants and asphalt, not fuel. So for every 100 barrels coming into a refinery, only about 73 barrels leaves as usable fuel. Natural gas does not need such extensive refining although an unknown amount needs to be used to separate the gas into its various components and a great deal, perhaps as much as 25 percent, is lost through pipeline leaks and to maintain pipeline pressure. Coal is usually burned to make electricity at an average efficiency of 35–40 percent. What this means, however, is that, e.g., oil resources that have an EROI of 1.1 megajoule returned per megajoule invested at the wellhead cannot provide an energy surplus for a society because not only does it cost about 10 percent of the energy obtained to get the energy out of the ground but then only 73 percent of the remaining oil is delivered to society. Thus this situation could not support itself. One needs a higher EROI.

Transportation costs: Oil weighs roughly 0.136 tons per barrel. Transportation by truck uses about 3400 BTU/ton-mile or 3.58 MJ per ton-mile. Transportation by fuel pipeline requires 500 BTU/ton-mile or 0.52 MJ per ton-mile. We assume that the average distance that oil moves from port or oil field to market is about 600 miles. Thus a barrel of oil, with about 6.2 gigajoules of contained chemical energy, requires on average about 600 miles of travel × 0.136 tons per barrel × 3.58 MJ per ton-mile = 292 MJ per barrel spent on transport or about 5% of the total energy content of a barrel of oil to move it to where it is used (◘ Table 18.1). If the oil is moved by pipeline (the more usual case), this percentage becomes about 1%. We assume that coal moves an average of 1500 miles, mostly by train at roughly 1720 BTU per ton-mile or about 1.81 MJ per ton-mile, so that the energy cost to move a ton of bituminous coal with about 32 MJ per kilogram (kg) (32 GJ/Ton) to its average destination is 1500 miles × 1.81 MJ per ton-mile = 2715 MJ per ton, or 2.715 GJ per ton of coal, which is about 8 percent (◘ Table 18.1). Line losses if shipped as electricity are roughly similar. So adding between 1 and 8 percent of the energy value of fuels for delivery costs does not seem unreasonable. Perhaps 25 percent of the energy in natural gas is used to move the gas down the pipeline, and an unknown but significant amount of energy is required to build and maintain the pipeline. We assume that these costs would decrease all EROIs by a conservative 5 percent to get it to the user; in other words the fuel must have an EROI of at least 1.05: 1 to account for delivery of that fuel.

Table 18.1

The energy cost of transporting oil and coal

	Energy cost (MJ/ton-mile)	Miles traveled	Energy cost(MJ)	Energy cost of energy unit delivered
Oil truck	3.58²	600	292	5%
Pipeline	0.52²	600	42	1%
Coal train	1.81²	1500	2715	8%

Sources: (1) Energy unit delivered: oil = 1 barrel = 6.2 GJ/barrel; Coal = 1 ton = 32 GJ/Ton. (2) Ref. [1].

Thus we find that our EROI_pou is about 32 percent less (17 percent nonfuel loss plus 10 percent to run the refinery plus about 5 percent transportation loss) than the EROI_mm indicating that at least for oil, one needs an EROI at the mine mouth of roughly 1.5:1 (i.e., 1.0/0.68) to get that energy to the point of final use.

18.7 Extended EROI: Calculating EROI at the Point of Use Correcting for the Energy Required for Creating and Maintaining Infrastructure

We must remember that usually what we want is energy services, not energy itself, which usually has little intrinsic economic usefulness, e.g., we want kilometers driven, not just the fuel that does that. That means that we need to count in our equation not just the “upstream” energy cost of finding and producing the fuels themselves but all of the “downstream” energy required to deliver the service (in this case transportation) including that for (1) building and maintaining vehicles, (2) making and maintaining the roads used, (3) incorporating the depreciation of vehicles, (4) incorporating the cost of insurance, (5) etc. All of these things are as necessary to drive that mile as the gasoline itself, at least in modern society. For the same reason, businesses pay some 55 or 60 cents per mile when a personal car is used for business, not just the 10 cents or so per mile that the gasoline costs. So in some sense, the energy required for delivering the service (a mile driven) is some four to five times the direct fuel costs, and this does not include the taxes used to maintain most of the roads and bridges. Now many of these costs, especially insurance, use less energy per dollar spent than fuel itself and also less than that for constructing or repairing automobiles or roads, and certainly this is not the case with the money used to deliver the fuel itself used in these operations.

On the other hand, the energy intensity of one dollar’s worth of fuel is some eight times greater than that for one dollar’s worth of infrastructural costs. ◘ Table 18.3 gives our estimates of the energy cost of creating and maintaining the entire infrastructure necessary to use all of the transportation fuel consumed in the United States. The energy intensities are rough estimates of the energy used to undertake any economic activity derived from the national mean ratio of GDP to energy (about 8.7 MJ/dollar), from the Carnegie-Mellon energy calculator website, and from Robert Herendeen (personal communication). Specifically, Herendeen estimates for 2005 that heavy construction uses about 14 MJ per dollar. Since in the 1970s insurance and other financial services had about half the energy intensities as heavy industry, our estimate of the energy required for infrastructure replacement and maintenance for the entire United States for 2005 is equal to about 38% of the energy used as fuel itself.

Our calculation, then, of adding in the energy costs of getting the fuel to the consumer in a usable form plus the energy cost of the infrastructure necessary to use the fuel is equal to about 0.32 plus 0.375, respectively, or about 0.695 in total. Thus the EROI at the wellhead necessary to provide transportation from crude oil is 3.3 to 1 (1/0.305). Thus to deliver the transportation services associated with one gallon of fuel put in a car or truck requires more than three gallons produced at the wellhead and probably similar proportions for other types of fuels.

Future research has extended our EROI to including the energy of all of the people and economic activity included directly and indirectly to deliver the energy. This is presented in the next chapter. Since, as we have indicated, roughly 10 percent of the economy is associated with getting energy (this includes even those farmers who grow the grain or laborers who build the airplanes used indirectly to feed laborers or to get engineers to the site), we might say that as a nation that part of the denominator for the EROI_ext would be 10 percent of all of the energy used in the country.

An important issue here is EROI vs. conversion efficiency. The EROI technically measures just the energy to get it to some point in society, usually the wellhead. But if we then say “to the consumer,” we have to include the refinery losses and energy costs and also the costs to deliver the fuel to the final consumer. It may also include the energy costs of maintaining the infrastructure to use that fuel. This is in reality a bleeding off of the energy delivered or a conversion efficiency of delivering one barrel of oil into transportation services. So whether we should say “the minimum EROI is 3.3:1” or, somewhat more accurately, that to deliver one barrel of fuel to the final consumer and to use it requires a little more than three barrels to be extracted from the ground is somewhat arbitrary, although the second way is technically more correct. Thus given that our national goal is to deliver 36 billion gallons of corn-based ethanol to our drivers, then if we were to include all the costs of getting and using that ethanol, something like 100 billion gallons would be required. Thus ethanol use is subsidized by the transportation infrastructure paid for with petroleum and its taxes and subsidies, and so on.

Thus by both economic (◘ Fig. 18.1) and energetic (i.e., assuming an EROI of 10:1) measures calculated here, it appears that at present roughly 10 percent of our economy is required to get the energy to run the other 90 percent, so that in some total sense (including the entire refining, conversion, and delivery chain), the mean EROI for our society is very roughly 10:1, and this seems to be true if numerator and denominator are in either dollars or in energy. (Note: Our use of relatively cheap coal and hydroelectricity, both with a relatively high EROI, lifts the actual ratio “at the wellhead” so that the EROI for energy delivered to society, but not the consumer, is roughly 20:1. By the time the energy is delivered to the consumer, that has fallen to roughly 10:1 considering the larger perspective of the entire energy delivery system—see below). The above analysis suggests that by the time the energy is delivered to the consumer the EROI is cut roughly by two-thirds (0.695). Thus by the time an alcohol fuel with an EROI of 3.3:1 is delivered to the consumer, that is, after the energy costs of refinement and blending, transport, and so on are included, it may no longer deliver an energy surplus. The reason for this decrease in end-user EROI is that it is energy services that are desired, not energy itself, and to create these energy services requires energy transformations that carry, at a minimum, large entropic (conversion efficiency) losses.

Thus we get EROI_ext “extended EROI,” which modifies that equation to include the energy required not only to get but also to use the energy. We define it formally here as:

${\mathrm{EROI}}_{\mathrm{ext}}=\frac{\mathrm{Energy}\ \mathrm{returned}\ \mathrm{to}\ \mathrm{society}}{\begin{array}{c}\mathrm{Energy}\ \mathrm{required}\ \mathrm{to}\ get,\\ {} deliver, and\ use\ \mathrm{that}\ \mathrm{energy}\end{array}}$

This concept is summarized in ◘ Fig. 18.2.

18.8 Why Should EROI Change Over Time? Technology Versus Depletion

There are two basic perspectives, with two very different groups of followers, relating to the long-term trend of efficiency in the production of oil (and other nonrenewable) resources. Many resource analysts emphasize the importance of depletion as humans exploit and eventually exhaust higher grades (i.e., more concentrated resources from more accessible deposits) over time. On the other hand, many resource analysts have expressed serious concern about the depletion of fuels and other resources over time. Why should this happen? Well essentially any business, such as a mining enterprise, is interested in making the maximum profit possible. The best first principle states that humans use the highest-quality sources of natural resources first as this would lead to higher profits. This concept was also of great interest to the classical economist David Ricardo. Given a choice, humans will grow crops on the more fertile soils, mine copper that is 10 rather than 1000 ft. deep, harvest timber from forests that are closer to roads and sawmills, fish larger, closer coastal concentrations, and so on. As the high-quality resources are depleted, lower-quality resources are used. This principle is well understood in economics based on work conducted 200 years ago by David Ricardo and is called the principle of diminishing returns.

18.8.1 EROI for US and North American Domestic Resources and Its Implications for the “Minimum EROI”

We start with historical, ecological, and evolutionary considerations, both because they have helped us a great deal to clarify our own perspectives on these issues and because, in the unsubsidized world where evolution operates, there are no bailouts or explicit subsidies, a very different situation from the one in which we operate in human society today.

In the past, Charles Hall worked with Cutler Cleveland and Robert Kaufmann to define and calculate the energy return on investment (EROI) of the most important fuels for the United States’ economy [e.g., 12, 13]. Since that time both Cleveland and Hall (and their coworkers) have undertaken additional and updated analyses for the US oil and gas industry [14–17, 27], and Gagnon and Hall [28] have done that for the world average of private companies (no analyst can get the required information from national oil companies such as Saudi Aramco). Our results indicate that there is still a very large energy surplus from fossil fuels—variously estimated as an EROI (i.e., EROI_mm) from perhaps 80 to 1 (domestic coal and perhaps some gas) to 11–18 to 1 (US) to 20 to 1 (world) for contemporary oil and gas globally (◘ Table 18.2). In other words, for every barrel of oil, or its equivalent, invested globally in seeking and producing more oil, some 10–20 barrels are delivered to society. Thus fossil fuels still provide a very large energy surplus, obviously enough to run and expand the human population and the very large and complex industrial societies around the world. This surplus energy of roughly 10–20 or more units of energy returned per unit invested in getting it, plus the large agricultural yields generated by fossil-fueled agriculture, allows a huge surplus quantity of energy, including food energy, to be delivered to society. This in turn allows most people and capital to be employed somewhere else other than in the energy industry. In other words these huge energy surpluses have allowed the development of all aspects of our civilization—both good and bad.

Table 18.2

Published EROI values for various fuel sources and regions

Resource	Year	Country	EROI (X:1)^a	Reference
Fossil fuels (oil and gas)
Oil and gas production	1999	Global	35	Gagnon (2009)
Oil and gas production	2006	Global	18	Gagnon (2009)
Oil and gas (domestic)	1970	US	30	Cleveland et al. [12], Hall et al. [13]
Discoveries	1970	US	8	Cleveland et al. [12], Hall et al. [13]
Production	1970	US	20	Cleveland et al. [12], Hall et al. [13]
Oil and gas (domestic)	2007	US	11	Guilford et al. [27]
Oil and gas (imported)	2007	US	12	Guilford et al. [27]
Oil and gas production	1970	Canada	65	Freise (2011)
Oil and gas production	2010	Canada	15	Freise (2011)
Oil, gas, and tar sand production	2010	Canada	11	Poisson and Hall (2011)
Oil and gas production	2008	Norway	40	Grandell (2011)
Oil production	2008	Norway	21	Grandell (2011)
Oil and gas production	2009	Mexico	45	Ramirez, in preparation
Oil and gas production	2010	China	10	Hu et al. (2013)
Fossil fuels (others)
Natural gas	2005	US	67	Sell et al. (2011)
Natural gas	1993	Canada	38	Freise (2011)
Natural gas	2000	Canada	26	Freise (2011)
Natural gas	2009	Canada	20	Freise (2011)
Coal (mine mouth)	1950	US	80	Cleveland et al. [12]
Coal (mine mouth)	2000	US	80	Hall and Day (2009)
Coal (mine mouth)	2007	US	60	Balogh et al. unpublished
Coal (mine mouth)	1995	China	35	Hu et al. (2013)
Coal (mine mouth)	2010	China	27	Hu et al. (2013)
Other nonrenewables
Nuclear	n/a	US	5 to 15	Hall and Day (2009), Lenzen (2008)
Renewables^b
Hydropower	n/a	n/a	>100	Cleveland et al. [12]
Wind turbine	n/a	n/a	18	Kubiszewski et al. (2010)
Geothermal	n/a	n/a	n/a	Gupta and Hall (2011)
Wave energy	n/a	n/a	n/a	Gupta and Hall (2011)
Solar collectors^b
Flat plate	n/a	n/a	1.9	Cleveland et al. [12]
Concentrating collector	n/a	n/a	1.6	Cleveland et al. [12]
Photovoltaic	n/a	n/a	6 to 12	Kubiszewski et al. (2009)
Passive solar	n/a	n/a	n/a	Cleveland et al. [12]
Passive Photovoltaic	2008	Spain	3 to 4	Prieto and Hall (2013)
Passive Photovoltaic	2008	n/a	10 to 15	Raugei et al. (2012)
Corn-based ethanol	n/a	US	0.8 to 1.6	Patzek (2004), Farrell et al. (2006)
Biodiesel	n/a	US	1.3	Pimentel and Patzek (2005)

From [16]

^aEROI values in excess of 5:1 are rounded to the nearest whole number

^bEROI values are assumed to vary based on geography and climate and are not attributed to a specific region/country. See [5, 16] for somewhat more comprehensive analyses which continue to evolve

Table 18.3

Breakdown of the downstream energy costs of refining, transporting, and using one barrel of oil

Process	Energy cost (%)	Energy Cost (GJ)^a
Nonfuel refinery products^b	17.0	1.11
Energy used in refining^c	10.0	0.51
Transport to consumer^d	5.0	0.23
Energy cost of transportation system^e	37.5	2.36
Final energy delivered to consumer	30.5	1.99

^a1 barrel of crude oil starts with 6.2 GJ

^bEIA accessed 2007 (► http://www.eia.doe.gov/bookshelf/brochures/gasoline/index.html)

^cSzklo and Schaeffer [26]

^dMudge et al. [28]

^eSee Table 18.2

But the problem with present substitutes to fossil fuels is that, of the alternatives available, none appear to have the desirable traits of fossil fuels. These include (1) sufficient energy density (◘ Table 4.1), (2) transportability, (3) relatively low environmental impact per net unit delivered to society, (4) relatively high EROI, (5) are obtainable on a scale that society presently demands, and (6) have the needed storage qualities. All of these would presumably greatly reduce the EROI of renewable fuels such as solar PV and wind, but the necessary calculations have not yet been undertaken. Wind, certainly, can make important contributions, but can it be used to generate a very large proportion of society’s energy with the required backups or storage? There is no good answer yet.

Thus it would seem that society, both the US and the world, is likely to be facing a decline in both the quantity and EROI of its principal fuels. Our next question is “what are the implications of this?”

18.9 The Surplus Available to Run the Rest of the Economy

We first generate a simplistic view of the economy in every day units to try to develop for the reader an explanation of how an economy obtains the energy needed for its own function and how differences in EROI might affect that. Assume for the moment that the United States’ economy runs 100 percent on domestic oil and that energy itself is not what is desired by the final consumer but rather the goods and services derived from the general economy. In 2016 the US gross domestic product was about 17 trillion dollars, and it used about 97.4 quadrillion BTUs (called quads, equal to 10¹⁵ BTUs), which is the metric equivalent of about 103 exajoules (1 EJ equals 10¹⁸ joules). Dividing the two we find that we used an average of about 6 megajoules (1 MJ equals 10⁶ joules) to generate on average one dollar’s worth of goods and services in 2017. By comparison, gasoline at $2.50 per gallon delivers about 52 MJ per dollar (at 131 MJ per gallon of gasoline), plus roughly another 20 percent to get that gasoline (extraction and refinery cost = 10 MJ), so if you spend one dollar on energy directly vs. one dollar on general economic activity, you would consume about 62/10 or 10 times more energy.

What is the energy “price” of the oil in the above example (1) to the country (either domestic or if it is imported) and (2) to the consumer—relative to the total economic activity of each entity? One can do some simple math. There are about 6.1 GJ in a standard 42 gallon barrel of oil, so the 97.4 exajoules of industrial energy the United States uses to run its economy for a year would require roughly 17 billion barrels of oil. At $50 per barrel, that amount of oil would take 850 billion dollars to purchase (or at $2.50 a gallon $ 1.8 trillion to the consumer), which is either about 5 percent of GDP or one-tenth if we consider it from the perspective of the consumer (the difference between the two estimates going to the oil companies after production for distribution and profits or to refineries, gas station attendants, etc. as inputs, profits, wages, delivery costs, etc.). Thus the price of energy delivered to the consumer is roughly twice that of the wellhead price (or about three times more than that if converted to electricity). But in 2017 we have to conclude that the energy cost of running our society is cheap.

Now assume that the real price of oil, that is, the price of oil relative to other goods and services, increased by three, that is, to $140 a barrel in today’s dollars (which it did briefly in 2008), and that the total size of the economy stayed the same—that is, some other components of the economy were diverted to pay for that oil. If that happened, then about (17 billion times $140 = $2.38 trillion/17 trillion) or 15 percent of the economy would be used to buy the oil to run the other 85 percent (i.e., that part not including the energy extraction system itself). If the price of oil increased to $250 per barrel, about one-third of all economic activity would be required to run the other two-thirds, and at $1000 a barrel, then the output of the entire economy, that is, 17 trillion dollars, would be required to generate the money to purchase the energy required to run the economy, i.e., there would be no net output. While in fact in a real economy there would be many adjustments, alternative fuels, and nuances, this analysis does at least give an overview of the relation of gross to net economic activity and the importance of high EROI in energy and economic terms to the profit of the rest of the economy. As the price of fuel increases (i.e., as its EROI declines), there are large impacts on the rest of the economy. These impacts can be especially influential because changes in the price of energy tend to impact discretionary, not baseline, spending. The implications are explored in the next chapter.

Of course most of our energy costs less than oil so that the 50 dollars a barrel we used in the example above translates to—in the real economy—the equivalent of about $35 a barrel equivalent at the source or $70 a barrel by the time the consumer gets the energy; hence we can assume for this scenario that on average about 5 percent of the dollar economy (i.e., $50 times 17 billion barrels or 800 billion out of 17 trillion dollars) is used just to purchase the energy that allows the rest of the economy to function, which produces the end products we want. This 5 percent of our total economic activity means that roughly 5 percent of all workers’ time, 5 percent of the energy used in their jobs, and 5 percent of the total materials consumed were used in some sense to get the energy to the final consumer to make the rest of the economy work. According to the official statistics of the US Energy Information Agency in 2017, the cost of energy to the consumer was about 5 percent of total incomes (◘ Fig. 18.1), so our numbers seem about right on average.

18.10 EROI of Obtaining Energy Through Trade

Now let us assume that the economy runs 100 percent on imported oil (this is the case for many small nations). An economy without enough domestic fossil fuels of the type it needs must import the fuels and pay for them with some kind of surplus economic activity. The ability to purchase the critically required energy depends upon what else it can generate to sell to the world as well as the fuel required to grow or produce that material. For example, Costa Rica to a large degree pays for its imported oil with exported bananas and coffee. These are commodities highly valued in the world and hence readily sold. They are also quite energy intensive to produce, however, especially when produced of the quality that sells in the rich countries. For example, bananas require an amount of money equivalent to about half of their purchase price to pay for the fuel and petrochemicals required for their production including their cosmetic quality. So in this case and in other such cases, the EROI for the imported fuel is the relation between the amount of fuel bought with a dollar or euro and the amount of dollar or euro profits gained by selling the goods and services for export. And the quantity of the goods or services exported to attain a barrel of oil depends upon the relative prices of the fuel vs. the exported commodities.

Kauffman [29] estimated from roughly 1950 through the early 1980s the energy cost of generating a dollar’s worth of our major US exports, e.g., wheat, commercial jetliners, etc., and also the chemical energy found in one dollar’s worth of imported oil. The concept was that the EROI for imported oil depended upon what proportion of an imported dollar’s worth of oil did you need to use to generate the commodities and hence the money obtained from overseas sales that you traded, in a net sense, for that oil. He concluded that before the oil price increases of the 1970s, the EROI for imported oil was about 25:1, very favorable for the United States, but that dropped to about 9:1 after the first oil price hike in 1973 and then down to about 3:1 following the second oil price hike in 1979. The ratio has returned to a more favorable level (from the perspective of the United States) since then because the price of exported goods has increased through inflation more rapidly than the price of oil. As oil prices increased again in this decade, however, and as more of the remaining conventional oil is concentrated in fewer and fewer countries and with their own internal use increasing, the future supply of abundant conventional oil in question, estimating the EROI of obtaining energy through trade may be very useful in predicting economic vulnerability in the near future (◘ Fig. 18.4). As of mid-2017, the United States imports nearly half of the oil it uses.

Now let’s revisit our previous example and assume that the US economy of 2007 runs entirely on imported oil rather than domestic oil. Neglecting for the moment debt and certain financial transactions such as cost of transport and foreigners investing in our banks, we, in a net sense, take oil, invest it in the economy, sell some of the products abroad to generate foreign exchange, and then use that foreign exchange to purchase oil from someone else—which we then use in the economy to generate more goods and services. To get the 1.2 trillion dollars’ worth of oil (17 billion barrels times $70 a barrel) that we would be importing under this scenario, we would have to sell at least 1.2 trillion dollars’ worth of our production abroad, which would require $1.2 trillion times 8.7 MJ used per average dollar generated in the economy or 10.4 EJ of our own energy. Thus about one-tenth (10.4 EJ of 105 EJ) of our total energy used and a roughly similar amount of our total economic activity would be required just to get the energy required to run the rest of the economy which produces the goods and services we want. Thus the EROI is about 10:1. This is still a pretty favorable return but only about 40 percent as favorable as it was in 1970 when it was 25:1 or even in 1998. To some degree we have managed to continue to do this through debt (much from Japan and China), which gives us a temporarily higher EROI. Were we to pay off this debt in the future and those who got the dollars wished to turn them into real goods and services (which seems a reasonable assumption), then we will have to take some substantial part of our remaining energy reserves out of the ground and convert it into fish, rice, beef, Fords, and so on that those people would be able to buy from us.

The dollar return on dollars invested is similar: 1.2 trillion of foreign exchange would be required to buy the oil (energy) that allows one to generate in the economy 17 trillion dollars, assuming that we ran only on imported oil. But if the price of oil inflates more rapidly than the prices of goods and services traded for the oil, then the portion of economic activity dedicated to raising foreign exchange to get that oil must increase unless the economy gets more efficient, a complex but probably oversold issue we will avoid here. Cleveland et al. [12] found a very high correlation between quality-corrected energy use and GDP from 1904 to 1984. Since then the economy has increased faster than energy use—although if one uses inflation rates calculated using the pre-Clinton era equation for CPI—such as that provided by ► www.shadowstatistics.com, the GDP declines, and the tight relation between GDP and energy use returns. Nonetheless, we believe that sharp increases (or decreases) in the price of imported oil will probably cause a series of structural changes to our economy that most people will not find particularly desirable. In fact, it is hard to ignore the coincident timing between the increases in the real price of oil culminating in the summer of 2008 and the subsequent financial collapse toward the end of the summer/fall 2008.

18.10.1 The Trade-off between EROI and Total Energy Used in Generating “Civilization”

The basic goods and services that we desire and require to have what we call modern civilization are highly dependent upon the delivery of net energy to society. This is a point made again and again by the authors quoted in the introduction to this chapter. But the total net energy that we have at our disposal, say roughly 90 percent of the 100 or so quads (or 105 EJ), would decrease to 80 if the cost of energy were to double (as what happened in the first part of 2008) or down to 60 if it were to double again and so forth, all of which is very possible. From this perspective, we think it very likely that EROI is likely to become an extremely important issue in defining our future economy and quality of life.

18.11 Conclusion

Our educated guess is that the minimum EROI required for a fuel that will deliver a given service (i.e., miles driven, house heated) to the consumer will be about 3:1 when all of the additional energy required to deliver and use that fuel are properly accounted for. This ratio would increase substantially if the energy cost of supporting labor (generally considered consumption by economists although definitely part of production here) or compensating for environmental destruction were included. While it is possible to imagine that one might use a great deal of fuel with a low EROI, say 2:1, to run an economy, this would mean that half of all economic activity was required to generate the other half, and we would be very, very poor. Even this would not be enough to do anything of economic utility, such as operating a truck. Thus we introduce the concept of “extended EROI” which includes not just the energy of getting the fuel but also that of transporting and using it. This process approximately triples the EROI required to use the fuel once obtained from the ground. Any fuel with an EROI less than the mean for society (about 10 to 1) may in fact be subsidized by the general petroleum economy. For example, fuels such as corn-based ethanol that have marginally positive EROIs (1.3:1) will be subsidized by the infrastructure support (i.e., construction and maintenance of roads and vehicles) undertaken by the main economy which is two-thirds based on oil and gas. These may be more important questions than the exact math for the fuel itself, although all are important.

Finally future analysis might even go so far as to include the money/energy to support and replace the oil worker. We believe this is important as there is little argument about the need to amortize the maintenance and depreciation of the oil derrick, so why not some prorated portion of medical care for the worker or education of his or her children for eventual replacement of the worn-out worker? Mainstream economists have some serious problems with this line of reasoning because they say that, e.g., medical care of workers or their children is consumption, not production. But, as with energy itself, a certain amount of consumption is essential for production and maybe we need to rethink when and how we draw the line between them. Perhaps it is best considered from the perspective of the two paragraphs above: as the EROI of fuels presumably declines into the future, then the rest of us will be supporting more and more workers in the energy industry, and there will be fewer and fewer net dollars and energy delivered to the rest of society. And if we are to support all the infrastructure to train engineers, physicians, and skilled laborers needed by society, we would need a far higher EROI from our primary fuels. This is explored in the next chapter.

Questions

1.
Define net energy, energy surplus, and EROI. Are they just different ways to say the same thing?
2.
Who were some of the pioneering thinkers about net energy?
3.
Why do they think of net energy as a “determinant of human culture”? Do you agree?
4.
Define the economic cost of energy.
5.
What are some of the precedents that led to the development of the concept of EROI? What was the role of fish?
6.
EROI can be calculated at various points, starting at the wellhead or the farm gate. Give some additional places in the energy use “food chain” where it might be useful to calculate EROI?
7.
Do you think that including the energy to maintain the infrastructure required to use a fuel should be included in an EROI assessment? Why or why not?
8.
What are some typical EROIs for various fuels in the US?
9.
Why would environmental considerations change an estimate for EROI?
10.
What is the approximate proportion of our economy attributable to energy costs?
11.
Explain how a nation with no energy resources invests energy to get energy.
12.
What is the relation between EROI and the amount of, e.g., education, medical care, and culture that a society can sustain?

References

1.
Modified from Hall, C.A.S., S. Balogh, and D.J.R. Murphy. 2009. What is the minimum EROI that a sustainable society must have? Energies 2: 25–47. which contains additional supporting references. SEE Hall, C.A.S. 2017. Energy return on investment (Springer) for a more thorough treatment of EROI.
2.
Odum, H.T. 1972. Environment, power and society. New York: Wiley-Interscience; Odum, H.T. 1973. Energy, ecology and economics. Royal Swedish Academy of Science. AMBIO 2(6):220–227.
3.
White, L.A. 1943. Energy and the evolution of culture. American Anthropologist 45: 335–356.Crossref
4.
Cottrell, F. 1955. Energy and society. New York: McGraw-Hill.
5.
Hall, C.A.S. 2017. Energy return on investment: A unifying principle for biology, economics and development. New York: Springer.Crossref
6.
Hamilton, J.D. 2009. Causes and consequences of the oil shock of 2007–08. Brookings Papers on Economic Activity, 1, Spring, 215–261.; Hamilton, J.D. 2011. Nonlinearities and the Macroeconomic Effects of Oil Prices. Macroeconomic Dynamics 15: 472–497.
7.
King, C.W. 2015. Comparing world economic and net energy metrics, Part 3: Macroeconomic Historical and Future Perspectives, Energies 8: 12997–13020.
8.
King, C., and Hall, C.A.S. 2011. Relating financial and energy return on investment: Sustainability: Special Issue on EROI, 3:810–1832.
9.
Hall, C.A.S. 1972. Migration and metabolism in a temperate stream ecosystem. Ecology 53: 585–604.Crossref
10.
Hall, C.A.S., and C.J. Cleveland. 1981. Petroleum drilling and production in the United States: Yield per effort and net energy analysis. Science 211: 576–579.Crossref
11.
Hall, C.A.S., C. Cleveland, and M. Berger. 1981. Energy return on investment for United States Petroleum, Coal and Uranium. In Energy and ecological modeling, ed. W. Mitsch, 715–724. Symp. Proc., Elsevier Publishing Co.; Hall, C.A.S., M. Lavine and J. Sloane. 1979. Efficiency of energy delivery systems: Part I. An economic and energy analysis. Environ. Mgment. 3: 493–504.
12.
Cleveland, C.J., R. Costanza, C.A.S. Hall, and R. Kaufmann. 1984. Energy and the United States economy: A biophysical perspective. Science 225: 890–897.Crossref
13.
Hall, C.A.S., C.J. Cleveland, and R. Kaufmann. 1986. Energy and resource quality: The ecology of the economic process, 1986. New York: Wiley.
14.
Cleveland, C.J. 2005. Net energy from the extraction of oil and gas in the United States. Energy: The International Journal 30 (5): 769–782.Crossref
15.
Hall, C.A.S., and D. Hanson, eds. 2011. Sustainability: Special Issue on EROI. Sustainability 3: 1–393
16.
Hall, C.A.S., J.G. Lambert, and S.B. Balogh. 2014. EROI of different fuels and the implications for society. Energy Policy 64: 141–152.Crossref
17.
Lambert, J., C.A.S. Hall, S. Balogh, A. Gupta, and M. Arnold. 2014. Energy, EROI and quality of life. Energy Policy 64: 153–167.Crossref
18.
Sundberg, U. 1992. Ecological economics of the Swedish Baltic Empire: An essay on energy and power, 1560–1720. Ecological Economics. 5: 51–72.MathSciNetCrossref
19.
See review by Farrell et al. 2006, [Farrell, A.E., R.J. Plevin, B.T. Turner, A.D. Jones, M. O'Hare, D.M. Kammen. 2006. Ethanol can contribute to energy and environmental goals. Science 311: 506–508.] as well as the many responses in the June 23, 2006 issue of Science Magazine for a fairly thorough discussion of this issue.
20.
Hall, C.A.S., B. Dale, and D. Pimentel. Seeking to understand the reasons for the different EROIs of biofuels. Sustainability 2011, 2011: 2433–2442.
21.
Murphy, D.J., C.A.S. Hall, and R. Powers. 2011. New perspectives on the energy return on investment of corn based ethanol. Environment, Development and Sustainability 13 (1): 179–202.Crossref
22.
Prieto, P., and C.A.S. Hall. 2012. Spain’s photovoltaic revolution: The energy return on investment. New York: Springer. Prieto and Hall; Raugei, M., Pere Fullana-i-Palmer, and Vasilis Fthenakis. 2012. The Energy Return on Energy Investment (EROI) of photovoltaics: Methodology and comparisons with fossil fuel life cycles. Energy Policy 45: 576–582.
23.
Raugei, M. Personal communication.
24.
Murphy, D., Hall, C.A.S., Cleveland, C., P. O’Conner. 2011. Order from chaos: A preliminary protocol for determining EROI for fuels. Sustainability: Special Issue on EROI, 1888–1907.
25.
Bullard, C.W., B. Hannon, and R.A. Herendeen. 1975. Energy flow through the US economy. Urbana: University of Illinois Press. Hannon, B. 1981. Analysis of the energy cost of economic activities: 1963 2000. Energy Research Group Doc. No. 316. Urbana: University of Illinois.; Herendeen, R., and C. Bullard. 1975. The energy costs of goods and services. 1963 and 1967. Energy Policy 3: 268.
26.
Costanza, R. 1980. Embodied energy and economic valuation. Science 210: 1219–1224.
27.
Guilford, M., C.A.S., Hall, P., O’Conner, and C.J., Cleveland. 2011. A new long term assessment of EROI for U.S. oil and gas: Sustainability: Special Issue on EROI. Pages 3: 1866–1887.; The Oil Drum: search for “Hall EROI”.
28.
Gagnon, N.C., A.S. Hall, and L. Brinker. 2009. A preliminary investigation of energy return on energy investment for global oil and gas production. Energies 2 (3): 490–503.Crossref
29.
Kauffman. 1986. Energy return on investment for imported petroleum. In Energy and resource quality: The ecology of the economic process, ed. C.A.S. Hall, C.J. Cleveland, and R. Kaufmann. New York: Wiley.

18. Energy Return on Investment