Chapter Four
Parrondo’s Principle
The Basic Principle
Widely acclaimed as the most significant advance in game-theoretic principles since the minimax process, “Parrondo’s Paradox”1 states that two games, each with a negative expectation, can be combined via deterministic or nondeterministic mixing of the games to produce a positive expectation. That is, a player may alternate regularly or randomly between two losing games to change the overall outcome to a winning one.
This counterintuitive principle can be illustrated as follows with games A and B: Game A is defined by tossing a biased coin C1 (or taking a biased random walk) that offers a probability of winning (Heads), P1 = 1/2 − α, and a probability of losing (Tails), 1 − P1 = 1/2 + α, where 0 ≤ α < 1/2 represents the bias against the player. Obviously, the condition for A to be fair is P1 = 1/2.
The expected value of game A is
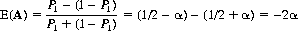
Game B entails two biased coins, C2 and C3, and is dependent on the player’s present capital. Coin C2 presents a probability of winning (Heads), P2 = x − α, with probability of losing (Tails), 1 − P2 = 1 − x + α, and is engaged when the player’s capital, F(t), equals 0 mod m units, m ≥ 2. With F(t) not a multiple of m, the player engages coin C3—with probability of winning, P3 = y − α, and probability of losing, 1 − P3 = 1 − y + α, where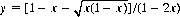 
. (Here y is chosen so that xy2 = (1 − x)(1 − y)2.) Although any value of x (between 0 and 1/2) can be called on to demonstrate Parrondo’s principle, only x = a2/(a2 + b2), for positive integers a and b with a < b, furnishes rational values of x and y2 (and thereby satisfies the anal-retentive). Parrondo adopted x = 1/10 for the original construct, and here we follow that precedent. Further, being engaged in a modulo-dependent game, B requires m ≥ 3 since a modulo-2 rule would allow the symmetry F(t) → −F(t) and thereby preclude the “losing + losing = winning” effect.
The wager for both A and B is one unit.
The combination of games A and B is illustrated in diagrammatic form in Figure 4-1 for the case m = 3.
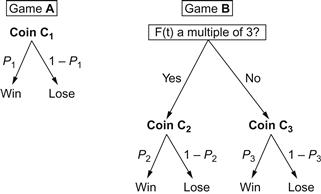
Figure 4-1 The basic Parrondo composite game.
The condition for game B to be fair is (1 − P2)(1 −P3)2 = P2 P32 since coin C3 is engaged twice as often as coin C2 (thus the probability of winning equals the probability of losing). Therefore, with the given values of P1, P2, and P3, game A shows a negative expectation for 1/2 > α > 0, while with the same α, and for m = 2 or 3, game B also has a negative expectation—although it is a winning game for m ≥ 4. Of the two subgames (with coins C2 and C3), coin C3 offers a positive expectation. (For the Parrondo principle to be in effect, all three coins cannot be negatively biased.)
To calculate the frequency of using coin C2, we define the variable G(t) = F(t) mod m. For m = 3, G(t)—which can take only three values, 0, 1, and 2, with assigned probabilities 5/13, 2/13, and 6/13, respectively—is a Markov chain with three states and a transition matrix
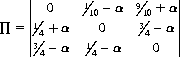
The entries for each row sum to 1, and the probability distribution P(t)—i.e., the vector whose components are the probabilities Pi(t) of G(t) = i for i = 0, 1, 2—obeys the evolution equation
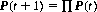
and, for t 
1, approaches a stationary distribution. That is, P(t) is the eigenvector of the matrix Π with eigenvalue 1. Specifically, the probability P0 of G(t) = 0 is computed as
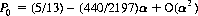
which is the probability of using coin C2. The probability of winning, Pwin, is then
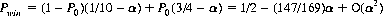
which, for α > 0 small yields a negative expectation, E(B):
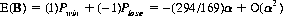
Combining games A and B to form game C, the probability of using coin C3 when playing the combined game is P′0—that is, P0 times the probability that we are playing game B:
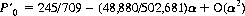
and the probability of winning, P′win, is then
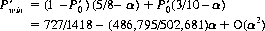
Thus, for α > 0 small, we have P′win > 0.5, and the principle holds. The expectation, E(C), of the composite game is
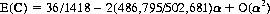
With α = 0.005, game A shows an expectation of −0.01, game B an expectation of −0.0087, and the composite game A + B an expectation of +0.0157.
(While it may not be immediately apparent, games A and B are not independent, being linked through available capital; changes in capital, however, may change the probabilities of subsequent games.)
At each discrete-time step, either game A or game B will be played. The pattern that selects the particular game is defined as the switching strategy—which can be a random-selection process with prescribed probabilities for A and B, a periodic pattern, or even a chaotic pattern (following a random-number sequence). In general, the shorter the switching period, the larger the return.
With the values of P1, P2, and P3 as specified, with α = 0 (reducing A and B to fair games), and with m = 3, the random-selection strategy is optimized when game A is selected with probability 0.4145 and game B with probability 0.5854 (although it produces a positive expectation of only 0.026).
Chaotic switching yields a higher rate of winning than that achieved by random switching. However, periodic switching produces the highest rate of winning since such a strategy favors playing the higher-winning subset in game B.
The pattern ABBAB offers by far the best strategy for the same parameters: an expectation of 0.0756, exceeding the random-selection strategy by a factor of almost 3. By comparison, the period-3 pattern, ABB, yields an expectation of 0.068. For m = 4, the pattern AB is unsurpassed (Ref. Ekhad and Zeilberger).
Parrondo has run a computer simulation averaged over one million trials, playing game A a times and then switching to game B for b plays—a combination designated [a,b]. Figure 4-2 shows the results for several switching sequences.
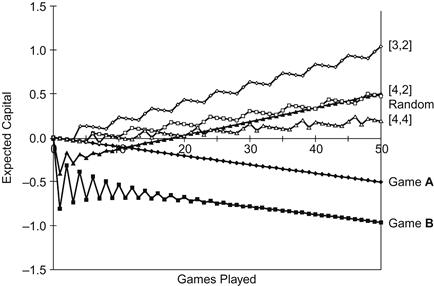
Figure 4-2 Capital-dependent games. Expected capital appreciation (depreciation) over 50 games (α = 0.005).
Alternating between the games produces a ratchet-like effect. If we envision a hill whose slope is related to a coin’s bias, then winning means moving uphill. In the single-coin game A, the slope is smooth; in the two-coin game B, the slope has a sawtooth profile. Alternating between A and B is akin to switching between smooth and sawtooth profiles—whatever gain occurs is trapped by the switch to the other game before subsequent repetitions of the original game can fulfill its negative expectation.
Etiology
The inspiration for Parrondo’s principle arose from the phenomenon known as Brownian motion—a random motion of molecular particles that manifests itself as noise. In 1992, Ajdari and Prost (Ref.) conceptualized a microscopic engine that, in operation, pushes particles to the left, but, if turned on and off repeatedly, moves particles to the right. This engine, known as a “flashing ratchet,” operates by exploiting the random (Brownian) motion of the particles.
Illustratively, consider a collection of electrically charged particles distributed randomly along a gradual slope. Assuming the particles to be in Brownian motion, they move left or right with equal probability, but with a slight drift down the slope. If we then superimpose along the slope an electric potential whose profile resembles the teeth of a saw, we will produce periodic energy peaks that rise steeply on the left side of the tooth and descend gradually along its right side. When the current is again switched off, the particles have a higher probability of crossing the peak of the potential to its immediate right than the one to its immediate left—since the troughs of the potential are offset to the right as the particles drift downward. With the current switched on a second time, many of the particles that had drifted left will be swept back into the trough from which they started. However, some of the particles that had drifted right will have traveled far enough to reach the adjacent trough. If the electric potential is switched on and off, or “flashed,” at the appropriate frequency, the charged particles in the flashing ratchet will ascend the slope, apparently defying gravity.3
Since the motions of molecular particles are analogous to the randomness of a coin-tossing sequence, Parrando was able to translate the mechanics of the flashing ratchet into the context of game theory.
One startling result of Parrondo’s principle suggests that a stock-market investor owning two “losing” stocks (i.e., stocks with declining prices) can—if he contrives to sell one stock during a brief uptick and shift those funds to another declining stock—overcome the general losing trend in both stocks. (Practical considerations—transaction fees, monotonically decreasing prices across the board—inhibit the operation of the Parrondo principle in this field.)
Other disciplines amenable to application of the Parrondo principle—extracting benefits from a detrimental situation—lie in the economic, genetic, sociological, and ecological realms. Certain biological processes may have long exploited the process to channel random forces toward the assembly of complex amino acids and thus create order out of disorder—and the development of complex life forms. Revolutionary changes in our understanding of the workings of nature may emerge.
Parrondo’s Domain
In general, for Parrondo’s principle to apply, three conditions need to be present:
1. An element of chance, as in Brownian motion, stock-market fluctuations, dice or coin throws
2. A ratchet-like asymmetry to the operating principles
3. Two basic dynamic processes that alternate regularly or randomly
R.D. Astumian (Ref.)4 has created a simple game to illustrate Parrondo’s principle. The playing field consists of five squares in a row, labeled as shown in Figure 4-3. Initially, a counter is placed on the START square and is then moved one square to the left or right in accordance with certain probabilistic rules.
Figure 4-3 A simple Astumian game.
Letλ be the probability of moving left from the START position and μ be the probability of moving left again (from the LEFT position). Finally, let ρ be the probability of moving right from the RIGHT position. These three numbers completely specify the game (designated by [λ, μ, ρ]), which, it should be noted, is symmetric if and only if λ = 1/2 and ρ = μ; the game is fair if and only if λμ = (1 − λ)ρ, which includes, but is not limited to, the symmetric case.
Consider two Astumian games, A and B, described by
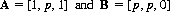
Both games, when played separately, are losing. In A, the initial move is leftward with certainty. In B, the counter can never reach the WIN square since ρ = 0. Yet by choosing a value of p sufficiently small, the composite game, A + B (each selected with probability 0.5), will have a winning probability arbitrarily close to 1.
After two moves of the A + B game, the counter will be in one of three positions (averaging over the four possible sequences AA, AB, BA, and BB):
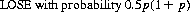
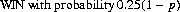
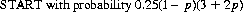
“Renormalizing” (to exclude those sequences that return to START), the probabilities for playing the game to WIN or LOSE are
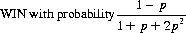
and, as noted, as p → 0, the WIN probability approaches 1.
If the A + B game is played by using one outcome of a die (p = 1/6), wins outnumber losses by 15 to 7. It remains a winning game for all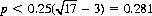 
.
Astumian games can also illustrate the Parrondo principle by combining two slow, losing games into a fast, winning one. Consider the two Astumian games described by
where n is a positive integer, and 0 < p < 1/2. We can calculate the renormalized probabilities for game Γ as
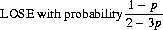
As p approaches 1/2, the probability of losing approaches 1.
For game Δn, the renormalized probabilities are
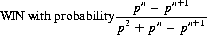
As n increases, the probability of losing approaches 1 independent of p.
For the randomly combined game, Γ + Δn, the renormalized probabilities of losing and winning are
With large values of n, the probability of losing in this combined game is less than 1/2 for p < 0.25. Ergo, Parrondo’s principle pertains for Γ + Δ n.
Both Γ and Δ n are games that are slow to resolve themselves into either LOSE or WIN outcomes. In game Γ, for n = 2 and p = 0.01, the counter will be in the START square 98.03% of the time:
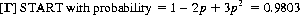
And, for game Δ n with the same parameters, the counter will be in the START square 99.98% of the time:
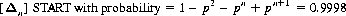
In the composite game Γ + Δ n, the counter remains in the START square less than 75% of the time:
After ten moves, the composite game will reach a resolution more than 76% of the time, whereas game Γ, the faster of the two individual games, will resolve itself less than 10% of the time.
Astumian games, although simple in format, nonetheless reflect the fundamental concept of how randomness may be converted to directed motion.
Multiplayer Games
A corollary to the Parrondo principle states that while random or periodic alternations of games A and B are winning, a strategy that chooses that game with the higher average return is losing (Ref. Dinis and Parrondo, 2002). Again, this principle runs counterintuitively.
Consider a large number N of players. At each turn of the game, a subset of φN players (0 < φ < 1), each with a known capital, selects either A or B—as defined initially—with the goal of maximizing expected average earnings. (The remaining (1 − φ)N players are inactive during this turn.) Let p0 (t) equal the fraction of players whose capital is a multiple of 3 at turn t. Then the average fractions of winning players in games A and B, respectively, are
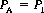
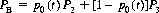
Following the stated maximization goal dictates the strategy:
Note that if game A is played continually, p0(t) tends to 1/3 since the capital F(t) constitutes a symmetric and homogeneous random walk. On the other hand, if game B is played continually, p0(t) tends to 5/13—and, insofar as p0(t) does not exceed 5/13, the maximization strategy continues to choose B. However, though this choice, by definition, maximizes the gain at each turn, it drives p0(t) toward 5/13—i.e., toward values of p0(t) where the gain is small. As an example, for φ = 1/2, α = 0, and p0(0) < 5/13, the maximization strategy chooses B forever—and the average capital barely appreciates.
Both the random and the periodic strategies choose game A even for p0 < 5/13. While these strategies will not produce earnings at each specific turn, they will drive p0 away from 5/13, whence the average capital will increase at a rate faster than that for the maximization (or “greedy”) strategy.
These concepts are illustrated in Figure 4-4, showing the appreciation (or depreciation) of average capital for φ = 0.675 and α = 0.005.
Figure 4-4 Multiplayer games. Expected appreciation (depreciation) of average capital over 50 turns (γ = 0.675, α = 0.005).
With these values of φ and α, B is a losing game, and since the maximization strategy here dictates playing B forever, the average capital decreases. Part of the “paradox” herein stems from the fact that neither the random nor the periodic strategy involves any information about the state of the system—whereas the strategy of choosing the game with the higher average return obviously does so. Dinis and Parrondo (Ref. 2003) describe the maximization strategy as “killing the goose that laid the golden eggs.” To increase earnings above this strategy, short-term profits must be sacrificed for higher future returns.
History-Dependent Parrondo Games
Parrondo’s original concept (derived from capital-dependent games) has since spawned history-dependent games and cooperative games (multiplayer rather than two opposing interests). The former encompasses those games whose outcomes are a function of previous game-states.5
Again, the underlying desideratum is “losing + losing = winning.” Game A is defined, as before, by the probability P = 1/2 − α of increasing the capital F(t). Game B′ is now defined by the probabilities of four biased coins, where the specific coin used at a given time t depends on the outcomes of the two immediately preceding time steps (“the game history”), as illustrated in Table 4-1. Or, expressed in diagrammatic form—Figure 4-5.
Table 4-1. The Parrondo History-Dependent Game
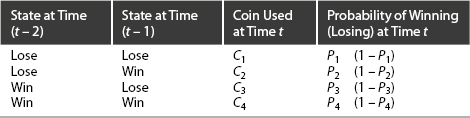
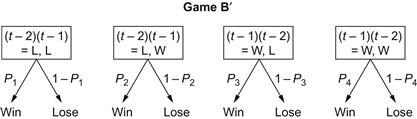
Figure 4-5 The basic history-dependent game.
Probabilities for game B′ are chosen, as before, to maintain rational numbers throughout the analysis:
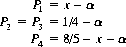(4-1)
The restriction P2 = P3 is effected to enable the different regions of the parameter space to be constructed as a three-dimensional figure.
Following Parrondo, we adopt the value x = 9/10 (P1 = 9/10 − α, P4 = 7/10 − α). Figure 4-6 shows the appreciation (depreciation) of capital F(t) with these probabilities and with α = 0.003 (averaged over the four initial conditions). We have assumed that the player tosses a fair coin twice, thereby establishing a “history,” but that the results of these tosses are not figured into the capital appreciation.
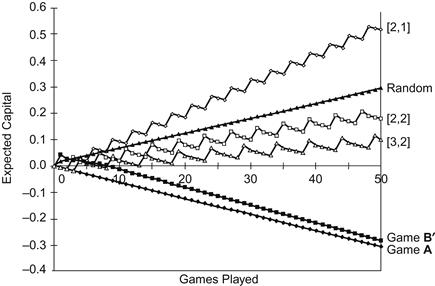
Figure 4-6 History-dependent games. Expected capital appreciation (depreciation) over 50 games (α = 0.003).
Similar to the analysis for capital-dependent games, history-dependent games can be represented as a discrete-time Markov chain with four states and a transition matrix. Figure 4-7 illustrates the Markov chain formed by the vector G′(n) = [F(n − 1) − F(n − 2), F(n) − F(n − 1)], whose four states are [−1, −1], [−1, +1], [+1, −1], and [+1, +1], where +1 indicates a win and −1 a loss.
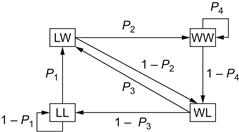
Figure 4-7 The discrete-time Markov chain for game B′.
The corresponding transition matrix is
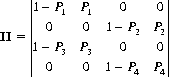
where columns and rows represent the four states LL, LW, WL, and WW in succession.
The stationary probabilities for this Markov chain can be computed as
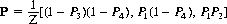(4-2)
where Z = P1 P2 + (1 + 2P1 − P3)(1 − P4) is a normalization constant. With the probabilities of Eq. 4-1, and with x = 9/10 and α = 0,
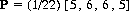
which yields a probability of winning for game B′,
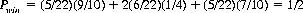
as expected for B′ with the bias removed (a fair game).
With the stationary probabilities of Eq. 4-2, we can derive
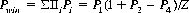
Setting Pwin < 1/2 for games A and B′ (losing) and Pwin > 1/2 for the composite randomized game, A + B′ (winning), we have the following constraints:
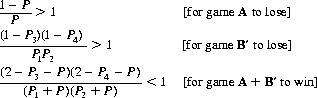(4-3)
where, in the second condition of Eq. 4-3, Pi is replaced by (Pi + P)/2, and the inequality reversed to obtain the third condition—viz., that A + B′ is winning instead of losing. With the probabilities of Eq. 4-1 (and x = 9/10), the first two conditions are satisfied for α > 0, while the third condition—and thus Parrondo’s principle—applies in the range 0 < α < 1/168.
A logical generalization of these results is the situation wherein both games to be combined are history-dependent (Ref. Kay and Johnson). Thus we define game B′ as before and game B″ similar to B′, but with Qi replacing Pi for the probability of winning at time t with coin C′i. Analogous to the second condition of Eq. 4-3, we have
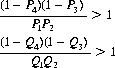(4-4)
for B′ and B″ to be losing. For the composite game B′ + B″, we define Ri as the probability of winning at time t. Then, for B′ + B″ to be winning, we must have
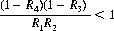
Randomly mixing the two games (with equal probability), this latter condition becomes
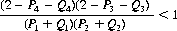
And, since B′ and B″ must be fair for α = 0, Eqs 4-4 with equality holding can be substituted for P1 and Q1. Therefore,
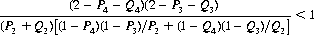(4-5)
for the combined game to be winning.
Using Parrondo’s probabilities, Eqs 4-1, with the added restriction that Q2 = Q3, the condition of Eq. 4-5 becomes
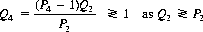
Without the restrictions P2 = P3 and Q2 = Q3, the more general condition for a winning composite game, B′ + B″, becomes
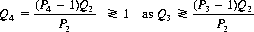
Periodic combinations of history-dependent games (as well as random combinations) have been investigated by Kay and Johnson (Ref). As with capital-dependent games, capital appreciation is greater with more rapid switching rates.
The parameter space for history-dependent games (the region where the combined game is winning) is substantially greater than for capital-dependent games—by a factor of about 55 (varying somewhat with the modulus and the playing frequency of each game). However, history-dependent games experience a lower rate of return.
Quantum games, spin systems, biogenesis, molecular transport, stock-market modeling, and noise-induced synchronization are but some of the many areas where these concepts have been applied. In general, it would seem that the phenomena amenable to analysis through history-dependent games are more extensive than those of capital-dependent games.
All-History Games
As well as the case where the specific coin played at time t depends on the outcome of the two immediately preceding time steps, we can generalize to any number of preceding time steps. That is, we consider a Markov process of order n that determines a new state based on the previous n states.
In some history-dependent games, there may be no (finite) limit on the number of previous states that can influence the new state. [A prominent example in game theory concerns computations of Grundy functions, wherein each function g(x) is dependent on g(0), g(1), …, g(x − 1).]
In determining the state at time t − r, it is not necessary to randomize the behavior of t − r as a function of r, since that state is already different whenever r is increased by 1—thereby doubling the size of the truth table6 and introducing a proportionate number of new coins.
The all-history–dependent game extends the columns of Table 4-1 backward to t − r and downward to encompass 2r terms and 2r coins engaged at time t and as many linear probabilities (Pi) as coins, as shown in Table 4-2 for r = 4.
Table 4-2. The All-History–Dependent Game
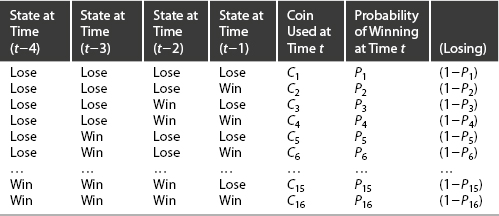
The array of wins and losses in Table 4-2 is isomorphic to a truth table with WIN and LOSE replacing the binary digits 0 and 1. Further, instead of the usual situation wherein multiple input states produce a single output state, Parrondo games entail binary input variables that are still binary, but outputs that are probabilities. This circumstance increases the number of possible Parrondo-type games hyperexponentially—viz.,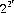 
—depending on which subset of the 2r coins shows heads.
In the example of capital-dependent games, each input state determines a coin, and that coin, rather than yielding Win or Lose directly, instead offers a probability of Winning or Losing.
Finally, it should be noted that the process described here is ergodic—that is, instead of using r units of time separately, we can achieve the same result by tossing r coins simultaneously.
Negative History
The question can be posed as to whether it is meaningful to consider that the coin used at time t can depend on future states t + 1 and t + 2.
Illustratively, if we express the Fibonacci recursion in terms of future events, we have
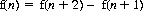
But the same values of f(n), as a difference of two events, can occur in infinitely many ways. So without precognition and without knowledge of both the recursion and two consecutive future values of f(·), it is not possible to reverse the process back to the present.
Quantum Parrondo Games
A protocol has been developed for a quantum version of history-dependent Parrondo games (Ref. Flitney, Ng, and Abbott). The probabilistic element is replaced by a superposition that represents all possible results in parallel. Game A becomes an arbitrary SU(2) operation on a qubit. Game B consists of four SU(2) operations controlled by the results of the previous two games. Superposition of qubits can be used to couple A and B and produce interference leading to payoffs quite different from those of the classical case. For example, in the conventional Parrondo game, the sequence AAB yields an effective payoff of 1/60 − 28∈/15 (positive for ∈ < 1/112). In the quantum version with the same sequence, a higher payoff results for all values of ∈ > 1/120.
Cooperative Games
Inspired, in turn, by history-dependent games, another family of Parrondo games, introduced by Raúl Toral (Ref. 2002) entails an ensemble of N players. At time t, one of the N players is selected at random. That player then chooses either game B or game A′ with probability 1/2, where the latter game consists of transferring one unit of his capital to another randomly selected player (from the remaining N − 1). By definition, A′ is a fair game (relative to the ensemble) since total capital is not changed but merely redistributed among the players. When game B is selected, a player risks his own capital (not that of the ensemble) to determine which coin to toss.
Figure 4-8 delineates the average capital per player versus time for the games A′ and B and the randomly mixed composite game A′ + B, where B is defined here by P2 = 1/10 − α, P3 = 3/4 − α, and α = 0.01. (Time is measured in units of games per player—that is, at time t, each of the N players has wagered t times on average for a total of Nt individual games. Here, N = 200.)
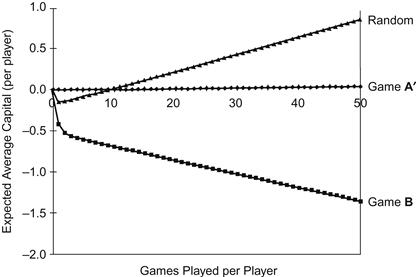
Figure 4-8 Cooperative games with capital dependence. Expected average capital appreciation (depreciation) per player over 10,000 games (200 players, α = 0.01).
This (again counterintuitive) result proves that the redistribution of capital can turn a losing game into a winning one, increasing the capital of the full ensemble of players. In fact, the average return from playing A′ + B is almost twice that from playing A + B with the same parameters (since game A′, wherein the capital of two players is changed by one unit, is equivalent to two games of A).
Replacing capital-dependent game B with history-dependent game B′ (a losing game unto itself, defined by the probabilities of Eq. 4-1 and with α = 0.01), we again observe the Parrondo principle for the composite game A′ + B′, as per Figure 4-9.
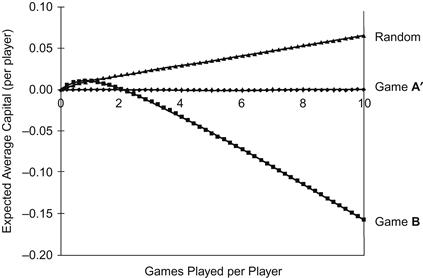
Figure 4-9 Cooperative games with history dependence. Expected average capital appreciation (depreciation) per player over 2000 games (200 players, α = 0.01).
To illustrate a further reach of the Parrondo principle, we assume that the players are arrayed (conventionally, in a ring) so that each layer has two immediate neighbors. Denoting player i’s capital after game t by Fi(t), the total capital of the group is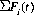 
. We can replace game A′ by game A″, wherein the randomly selected player i transfers one unit of his capital to either of his immediate neighbors with a probability proportional to the difference in capital between player i and his neighbor. That is,
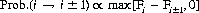
with Prob.(i → i + 1) + Prob.(i → i − 1) = 1 (and with F0 = F200 and F201 = F1). If i is the poorest of the three players, no transfer takes place, since the redistribution of capital in A″ always flows from richer to poorer players. The combined game A″ + B is illustrated in Figure 4-10.
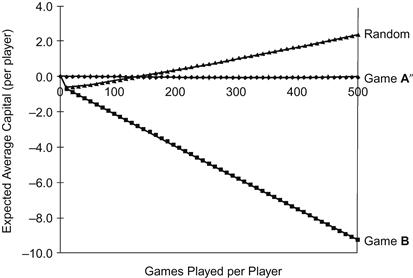
Figure 4-10 Cooperative games with redistribution from richer to poorer neighbors. Expected average capital appreciation (depreciation) per player over 100,000 games (200 players, α = 0.01).
In each of these randomly mixed games, the expected average capital per player increases linearly with the number of games per player after a short initial nonlinear period. In each case, we can note that the redistribution of capital (without altering the total capital per se) actually increases the total capital available when combined with other losing games—ergo, redistribution of capital as defined here is beneficial for all N players.
In another version of this cooperative game (Ref. Toral, 2001), the N players compete, in turn, against a banker who collects or pays out the wager. Here, in game B″, the probability of the ith player winning at time t depends upon the state of his two neighbors, players i + 1 and i − 1. Specifically, this probability is given by
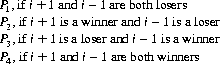
Whether a player is a winner or loser depends solely on the result of his most recent game. In game A, the selected player wins with probability P. Computer simulation has shown that there are sets of these probabilities wherein the alternate playing of A and B″ yields positive-expectation results, although A and B″ separately are losing or fair games (as per the Parrondo principle). For example, with game A (fair) defined by P = 0.5, and game B″ (losing) defined by P1 = 1.0, P2 = P3 = 0.16, and P4 = 0.7, the average capital per player versus t for the composite game A + B″ is illustrated in Figure 4-11. To initialize this game, we assume that each player tosses a fair coin to determine his status as a winner or loser. Random mixing and alternating with an AAB″B″ pattern yield virtually identical results.
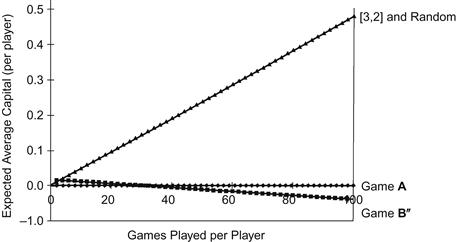
Figure 4-11 Cooperative games with neighbor dependence. Expected average capital appreciation (depreciation) per player over 20,000 games (200 players) (solid triangles are hidden behind the open triangles).
Cooperative games introduce the novel concept that combining two losing (or nonwinning) games to produce a winning game results from interactions among the players.
The Allison Mixture
Another form of Parrondo’s principle, designated the Allison mixture, is formulated as follows.
Consider two sequences of binary random numbers, S1 and S2, with respective means μ1 and μ2. (By definition, each sequence has a zero autocorrelation.) We now generate a third sequence by randomly scrambling the first two. For this purpose, we use two biased coins: C1, tossed when we are in S1 and which indicates “shift to S2” with probability p1 and “don’t shift” with probability 1 − p1; and C2, tossed when we are in S2 and which indicates “shift to S1” with probability p2 and don’t shift with probability 1 − p2.
Specifically, we begin (arbitrarily) at position n in S1 and then toss coin C1 to determine either a move to the n + 1 position in S2 or to the n + 1 position in S1. When in S2, we toss coin C2 to determine similar actions: to shift back to S1 or move on to the next position in S2, and so forth.
It has been proved (Ref. Allison, Pearce, and Abbott) that the autocorrelation ρ for the new sequence is
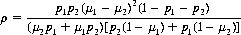
Thus, a random mixing of two random sequences has produced, counterintuitively, a sequence with less randomness—presuming that the two means and the two sequence-shifting probabilities are not equal.
Random sequences S1 and S2 contain maximal information in the Shannon sense; when μ1 ≠ μ2, the back-and-forth shifting process is irreversible, the generated sequence contains redundancy, and we therefore lose information (i.e., ρ ≠ 0). Further, when p1 + p2 ≠ 1 (biased coins), switching between S1 and S2 leads to memory persistence and concomitant correlation in the generated sequence.
Both the Allison mixture and the Parrondo effect require an asymmetry to interact with random phenomena. (The Allison mixture is also valid for sequences other than binary.)
Finally, it should be noted that, for all the various games discussed herein, Parrondo’s principle can be reversed to effect “winning + winning = losing.” The nature of such a reversal renders it a matter of primarily academic interest.
REFERENCES
Adjari A, Prost J, (1992). Drift Induced by a Periodic Potential of Low Symmetry: Pulsed Dielectrophoresis. C. R Acad. Sci. (Paris) ser. II.315:1635–1639.
Allison, A., C. E. M. Pearce, and Derek Abbott “Finding Key Words Amongst Noise: Automatic Text Classification Without Parsing,” in Janós Kertéz, Stefan Bornholdt, and Rosario N. Mantagna (eds.), Proceedings SPIE Noise and Stochastics in Complex Systems and Finance, 6601, June 2001.
Almeida J, Peralta-Salas D, Romera M, (2005). Can Two Chaotic Systems Give Rise to Order?. Physics D.200:124–132.
Astumian RD, (2001). Making Molecules into Motors. Scientific American.285(7):56–64.
Dinis, L., and J. M. R. Parrondo, “Parrondo’s Paradox and the Risks of Short-Range Optimization,” 2002, http://arxiv/prg/pdf/cond-mat/0212358.
Dinis L, Parrondo JMR, (2003). Optimal Strategies in Collective Parrondo Games. Europhysics Letters.63:319–325.
Ekhad, S. B., and D. Zeilberger, “Remarks on the Parrondo Paradox,” 2000, www.math.rutgers.edu/~zeilberg/mamarim/mamarimhtml/parrondo.html.
Epstein Richard A, (2007). Parrondo’s Principle: An Overview. In: Ethier Stewart, Eadington William R, eds. Optimal Play. Mathematical Studies of Games and Gambling. Institute for the Study of Gambling and Commercial Gaming, University of Nevada: 471–492. .
Ethier SN, (2007). Markov Chains and Parrondo’s Paradox. In: Stewart Ethier, William Eadington, eds. Optimal Play. Mathematical Studies of Games and Gambling. Reno: Institute for the Study of Gambling and Commercial Gaming, University of Nevada;: 493–506. .
Flitney AP, Ng J, Abbott Derek, (2002). Quantum Parrondo’s Games. Physics A.314:35–42 [http://xxx.lanl.gov.]
Harmer GP, Abbott Derek, (38; Abbott (1999). Parrondo’s Paradox. Statistical Science.14(2):206–213.
Harmer GP, Abbott Derek, Taylor PG, Parrondo JMR, (2000). Parrondo’s Paradoxical Games and the Discrete Brownian Ratchet. In: Abbott Derek, Kiss LB, eds. Melville, NY: American Institute of Physics;: 189–200. Proceedings 2nd International Conference on Unsolved Problems of Noise and Fluctuations,; 511.
Kay RJ, Johnson NE, (2003). Winning Combinations of History-dependent Games. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics.67(5):056128-1–056128-6.
Martin H, von Baeyer HC, (2004). Simple Games to Illustrate Parrondo’s Paradox. American Journal of Physics.72(5):710–714.
Parrondo JMR, Dinis L, (2004). Brownian Motion and Gambling: From Ratchets to Paradoxical Games. Contemporary Physics.45:147–157.
Parrondo JMR, Harmer GP, Abbott Derek, (2000). New Paradoxical Games Based on Brownian Ratchets. Physical Review Letters.85(24):5226–5229.
Toral R, (2001). Cooperative Parrondo’s Games. Fluctuation and Noise Letters.1(1):L7–L12.
Toral R, (2002). Capital Redistribution Brings Wealth by Parrondo’s Paradox. Fluctuation and Noise Letters.2(4):L305–L311.
Bibliography
Arena P, Fazino S, Fortuna L, Maniscalco P, (2003). Game Theory and Non-linear Dynamics: The Parrondo Paradox Case Study. Chaos, Solitons, and Fractals.17:545–555.
Berresford GC, Rocket AM, (2003). Parrondo’s Paradox. International Journal of Mathematics and Mathematical Sciences.62:3957–3962.
Blakeslee, Sandra., “Paradox in Game Theory: Losing Strategy That Wins,” New York Times, January 25, 2000.
Cleuren B, Van den Broeck CC, (2004). Primary Parrondo Paradox. Europhysics Letters.67(2):151–157.
Cleuren B, Van den Broeck C, (2004). Optimizing Strategies in the Primary Parrondo Paradox. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics.70:067104-1–067104-4.
Davies PCW, (2001). First Steps in the Origin of Life in the Universe. In: Chela-Flores J, Tobias T, Raulin F, eds. Proceedings of the Sixth Trieste Conference on Chemical Evolution. Kluwer Academic: 13–20. .
Dijkstra EW, (1990). Making a Fair Roulette from a Possibly Biased Coin. Information Processing Letters.36:193.
Doering CR, (1995). Randomly Rattled Ratchets. Nuovo Cimento.17:685–697.
Durrett R, Kesten H, Lawler G, (1991). Making Money From Fair Games. In: Durrett R, Kesten H, eds. Random Walks, Brownian Motion, and Interacting Particle Systems. Birkhäuser: 255–267. .
Feldman D, Impagliazzo R, Naor M, Nisan N, Rudich S, Shamir A, (1993). On Dice and Coins: Models of Computation for Random Generation. Information and Computation.104:159–174.
Gargamo L, Vaccaro U, (1999). Efficient Generation of Fair Dice with Few Biased Coins. IEEE Transactions on Information Theory.45:1600–1606.
Harmer GP, Abbott Derek, (2002). A Review of Parrondo’s Paradox. Fluctuation Noise Letters.2:R71–R107.
Harmer GP, Abbott Derek, (1999). Losing Strategies Can Win by Parrondo’s Paradox. Nature.102(6764):864.
Harmer GP, Abbott Derek, Taylor PG, Pearce CEM, Parrondo JMR, (2000). Information Entropy and Parrondo’s Discrete-Time Ratchet. In: Broomhead E, Luchinskaya A, McClintock PVE, Mullin T, eds. American Institute of Physics: 544–549. Proceedings Stochastic and Chaotic Dynamics in the Lakes; 502.
Hoeffding W, Simons G, (1970). Unbiased Coin Tossing with a Biased Coin. Annals of Mathematics and Statistics.41:341–352.
Itoh T, (1996). Simulating Fair Dice with Biased Coins. Information and Computation.126(1):78–82.
Kestenbaum D, (1997). Sand Castles and Cocktail Nuts. New Scientists.154:25–28.
Klarreich Erica, (2001). Playing Both Sides. Sciences.41(1):25–29.
Meyer, David A., “Noisy Quantum Parrondo Games,” Proceedings of the SPIE, 2003.
Parrondo JMR, (1996). How to Cheat a Bad Mathematician. In: EEC HC&M Network on Complexity and Chaos. Institute for Scientific Interchange Foundation.
Parrondo, J.M.R., “Parrondo’s Paradoxical Games,” http://seneca.fis.ucm.es./parr/GAMES/.
Parrondo JMR, de Cisneros BJ, (2000). Juegos Paradójicos y Máquinas Térmicas Brownianas. Revista Española de Física.14(3):24–28.
Pearce CEM, (2000). On Parrondo’s Paradoxical Games. In: Abbott LB, Kiss , eds. American Institute of Physics: 201–206. Proceedings of the 2nd International Conference on Unsolved Problems of Noise and Fluctuations; 511.
Percus OE, Percus JK, (2002). Can Two Wrongs Make A Right? Coin-Tossing Games and Parrondo’s Paradox. Mathematics Intelligencer.24:68–72.
Pyke, R., “On Random Walks and Diffusions Related to Parrondo’s Games,” http://lanl.arxiv.org/abs/math/0206150.
Tang TW, Allison A, Abbott Derek, (2004). Investigation of Chaotic Switching Strategies in Parrondo’s Games. Fluctuations and Noise Letters.4(4):L585–L596.
Van den Broeck C, Cleuren B, (2004). Parrondo Games with Strategy. Proceedings SPIE Noise in Complex Systems and Stochastic Dynamics II.5471:109–118.
Velleman D, Wagon S, (2000). Parrondo’s Paradox. Mathematics in Education and Research.9:85–90.
1 After Juan Parrondo, a physicist at the Universidad Complutense de Madrid. The seminal paper expounding on Parrondo’s innovation is due to Gregory Harmer and Derek Abbott (Ref. 1999).
2 This observation is credited to Stewart Ethier.
3 The flashing ratchet has been accused of violating the second law of thermodynamics by giving rise to more order (directed motion) than is fed into it. The defense brief holds that an outside source is here acting on the system—viz. the energy required to switch the potential on and off. Maxwell’s demon was not called to testify.
4 The original game failed to satisfy condition 2. We present here the corrected version (Ref. Martin and von Baeyer).
5 Capital-dependent games under modulo-arithmetic rules are not consonant with many processes such as biology and biophysics.
6 A truth table, in Boolean logic (or in switching theory), consists of r binary input states, each of which yields one (deterministic) binary output and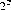 
different truth tables.