As discussed in the previous chapter, DQN uses the Q-network to estimate the state-action value function, which has a separate output for each available action. Therefore, the Q-network cannot be applied, due to the continuous action space. A careful reader may remember that there is another architecture of the Q-network that takes both the state and the action as its inputs, and outputs the estimate of the corresponding Q-value. This architecture doesn't require the number of available actions to be finite, and has the capability to deal with continuous input actions:
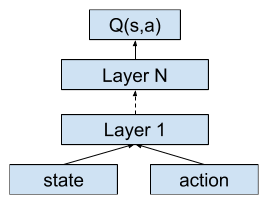
If we use this kind of network to estimate the state-action value function, there must be another network that defines the behavior policy of the agent, namely outputting a proper action given the observed state. In fact, this is the intuition behind actor-critic reinforcement learning algorithms. The actor-critic architecture contains two parts:
- Actor: The actor defines the behavior policy of the agent. In control tasks, it outputs the control signal given the current state of the system.
- Critic: The critic estimates the Q-value of the current policy. It can judge whether the policy is good or not.
Therefore, if both the actor and the critic can be trained with the feedbacks (state, reward, next state, termination signal) received from the system, as in training the Q-network in DQN, then the classic control tasks will be solved. But how do we train them?