Based on the preceding policy improvement bound, the following algorithm is developed:
Initialize policy;
Repeat for each step:
Compute all advantage values;
Solve the following optimization problem:
;
Until convergence
In each step, this algorithm minimizes the upper bound of 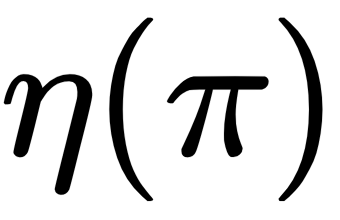 , so that:
, so that:

The last equation follows from that 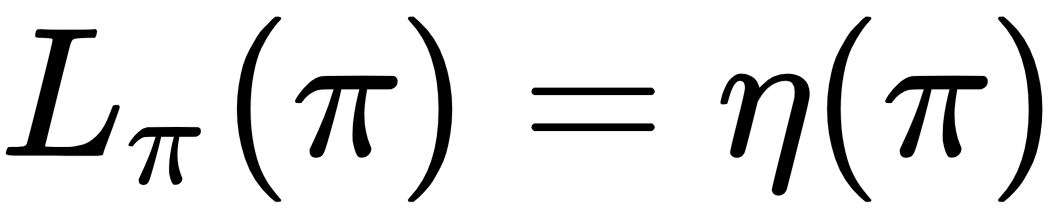 for any policy
for any policy  . This implies that this algorithm is guaranteed to generate a sequence of monotonically improving policies.
. This implies that this algorithm is guaranteed to generate a sequence of monotonically improving policies.
In practice, since the exact value of 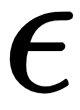 in
in  is hard to calculate, and it is difficult to control the step size of each update using the penalty term, TRPO replaces the penalty term with the constraint that KL divergence is bounded by a constant
is hard to calculate, and it is difficult to control the step size of each update using the penalty term, TRPO replaces the penalty term with the constraint that KL divergence is bounded by a constant 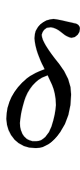 :
:

But this problem is still impractical to solve due to the large number of constraints. Therefore, TRPO uses a heuristic approximation that considers the average KL divergence:
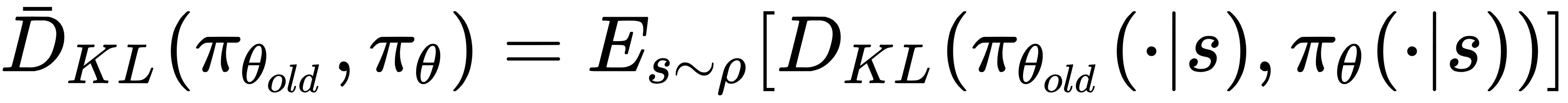
This leads to the following optimization problem:
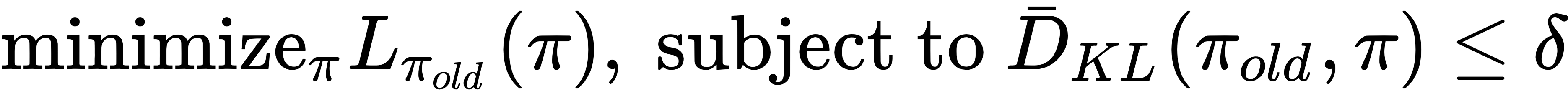
In other words, by expanding 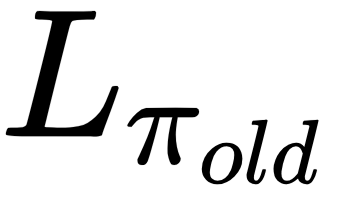 , we need to solve the following:
, we need to solve the following:
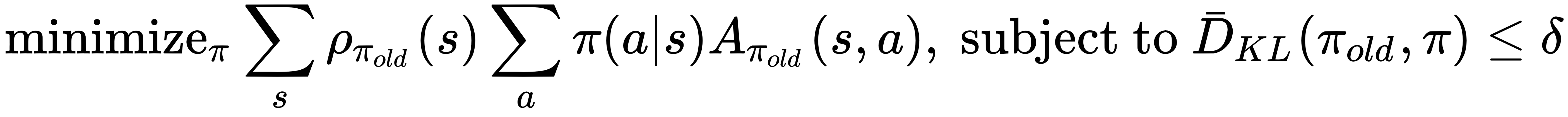
Now, the question is: how do we optimize this problem? A straightforward idea is to sample several trajectories by simulating the policy 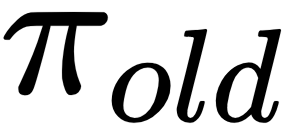 for some number of steps and then approximate the objective function of this problem using these trajectories. Since the advantage function
for some number of steps and then approximate the objective function of this problem using these trajectories. Since the advantage function 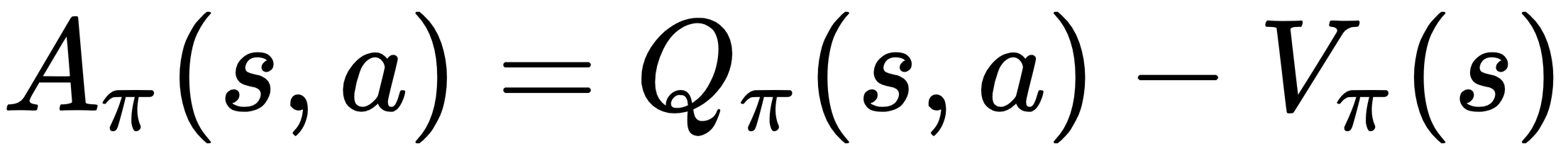 , we replace
, we replace 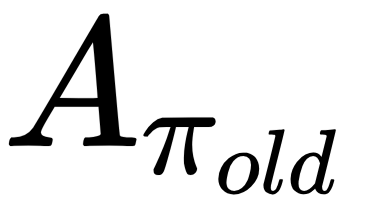 with by the Q-value
with by the Q-value 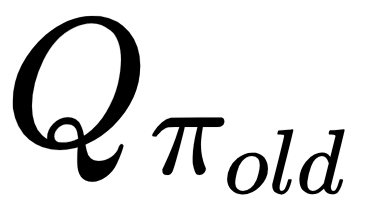 in the objective function, which only changes the objective by a constant. Besides, note the following:
in the objective function, which only changes the objective by a constant. Besides, note the following:
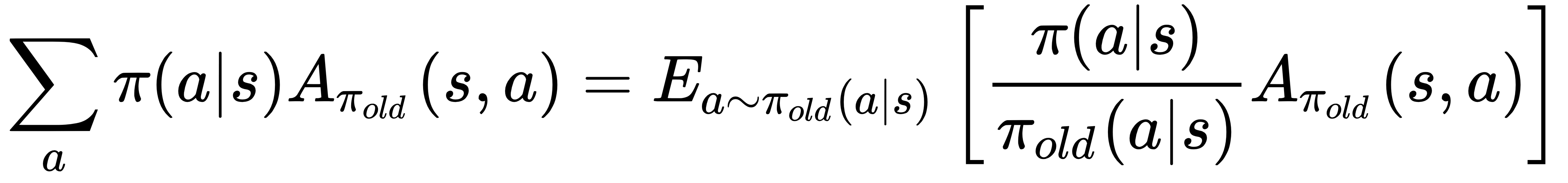
Therefore, given a trajectory 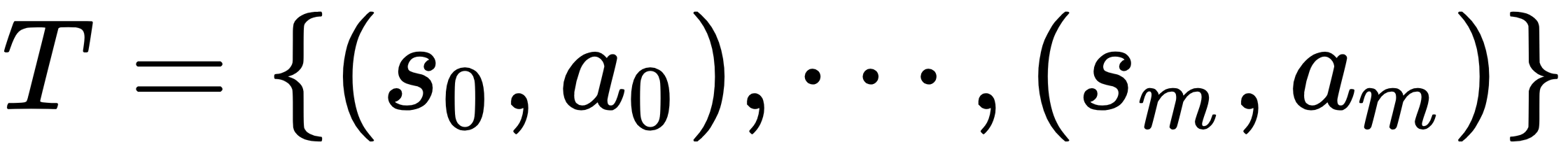 generated under policy
generated under policy 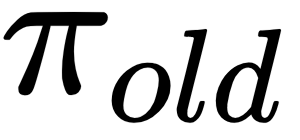 , we will optimize as follows:
, we will optimize as follows:
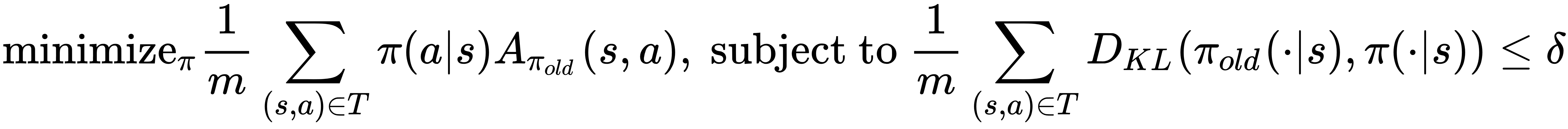
For the MuJoCo control tasks, both the policy  and the state-action value function
and the state-action value function 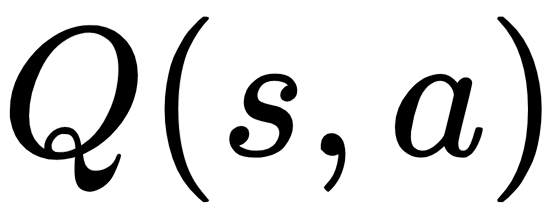 are approximated by neural networks. In order to optimize this problem, the KL divergence constraint can be approximated by the Fisher information matrix. This problem can then be solved via the conjugate gradient algorithm. For more details, you can download the source code of TRPO from GitHub and check optimizer.py, which implements the conjugate gradient algorithm using TensorFlow.
are approximated by neural networks. In order to optimize this problem, the KL divergence constraint can be approximated by the Fisher information matrix. This problem can then be solved via the conjugate gradient algorithm. For more details, you can download the source code of TRPO from GitHub and check optimizer.py, which implements the conjugate gradient algorithm using TensorFlow.