
Given a larger number of cost/output observations, we can apply regression analysis to estimate the dependence of costs upon the output level and thus obtain an estimate of the marginal cost . 2 Since we wish to estimate the cost function of a particular firm,
The principles of regression analysis and the major problems associated with the use and interpreta- tion of the results of this method were discussed in a self-contained section of Chapter 5. The discussion in this chapter presumes your familiarity with the earlier section.
we must use time-series data from that firm. This necessity raises some of the standard problems with time-series data: If over the period of the observations some factors have changed, the results of regression analysis will be less reliable. For example, factor prices may change because of inflation or market forces in the factor markets, or factor productivities may change because of changing technology and worker efficiency. To largely eliminate these problems the cost data should be deflated by an appropriate price index, and time should be inserted as an independent variable in the regression equation. Any trend in the relative prices or productivities will then be accounted for by the coefficient of the time variable.
Regression analysis of time-series cost data is quite susceptible to the problems of measurement error. The cost data should include all costs that are caused by a particular output level, whether or not they are yet paid for. Maintenance expense, for example, should be expected to vary with the rate of output, but it may be delayed until it is more convenient to close down certain sections of the plant or facilities for maintenance purposes. Hence the cost that is caused in an earlier period is not recorded until a later period and is thus likely to understate the earlier cost level and to overstate the later cost level. Ideally, our cost/output observations should be the result of considerable fluctuations of output over a short period of time with no cost/output matching problems.
Example: Suppose the weekly output and total variable costs of an ice cream plant have been recorded over a three-month period, as shown in Table 8-2. Output of the product varies from week to week because of the rather unpredictable nature of the milk supply from dairies and the impossibility of holding inventories of the fresh milk for more than a few days.
It is apparent from the data supplied that total variable costs tend to vary posi-
Table captionTABLE 8-2. Record of Output Levels and Total Variable Costs for an Ice Cream Plant
Week Ending | Output (gallons) | Total Variable Costs ($) |
Sept. 7 | 7,300 | 5,780 |
Sept. 14 | 8,450 | 7,010 |
Sept. 21 | 8,300 | 6,550 |
Sept. 28 | 9,500 | 7,620 |
Oct. 5 | 6,700 | 5,650 |
Oct. 12 | 9,050 | 7,100 |
Oct. 19 | 5,450 | 5,060 |
Oct. 26 | 5,950 | 5,250 |
Nov. 2 | 5,150 | 4,490 |
Nov. 9 | 10,050 | 7,520 |
Nov. 16 | 10,300 | 8,030 |
Nov. 23 | 7,750 | 6,350 |
' A 3
tively with the output level in this ice cream plant. But what is the form of the relationship? The specification of the functional form of the regression equation has resounding implications for the estimate of the marginal cost curve that will be indicated by the regression analysis. If we specify total variable costs as a linear function of output, such as TVC = a + bQ, the marginal cost estimation generated by the regression analysis will be the parameter b, since marginal cost is equivalent to the derivative of the total variable cost function with respect to the output level. In Figure 8-4 we show, for a given collection of data observations, the consequent average variable costs and marginal cost curves that would be generated by regression analysis using a linear specification of the relationship. Since average variable costs are total variable cost divided by output level Q, the AVC curve will decline to approach the MC curve asymptotically.
Alternatively, for the same group of data observations, if we specify the functional form as a quadratic such as TVC = a + bQ + cQ 2 , the marginal cost will not
FIGURE 8-4. Linear Variable Cost Function
C-l d _P [q
be constant but will rise as a constant function of output. In Figure 8-5 we show the hypothesized quadratic relationship superimposed upon the same data observations, with the consequent average variable cost and marginal cost curves illustrated in the lower half of the figure.
Finally, if we hypothesize that the functional relationship is cubic; such as TVC = a + bQ — cQ 2 + dQ i , the marginal cost estimate generated by regression analysis will be curvilinear and will increase with the square of the output level. Figure 8-6 illustrates the cost curves consequent upon a cubic expression of the cost/output relationship. Alternatively, a power function or other multiplicative relationship may be appropriate.
Which form of the cost function should we specify? Since the results of the regression analysis will be used for decision-making purposes, we must be assured that the marginal and average cost curves generated are the most accurate representations of the cost/output relationships. By plotting the total variable cost data against out-
FIGURE 8-5. Quadratic Variable Cost Function
FIGURE 8-6. Cubic Variable Cost Function
put, we may be able to ascertain that one of the above three functional forms best represents the apparent relationship existing between the two variables, and we may thus confidently continue the regression analysis using this particular functional form.

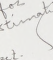
If it is not visually apparent that one particular functional form is the best representation of the apparent relationship, it may be necessary to run the regression analysis first with a linear functional form and later with one or more of the other functional forms in order to find which equation best fits the data base. You will recall from Chapter 5 that the regression equation that generates the highest coefficient of determination (R 2 ) is the equation that explains the highest proportion of the variability of the dependent variable, and it can thus be taken to be the best indication of the actual functional relationship that exists between the two variables.
Example: Fitting a linear regression equation to the cost-output pairs shown in Table 8-2 resulted in the following computer output:

( 8 - 2 )
with a standa33 error of estimate of 182.02 and a standard error of the regression coefficient of 0.0313. The coefficient of determination ( R 2 ) was 0.97614.
Note that this linear regression equation explains 97.614 percent of the variation in TVC as resulting from the variation in the output level. 3
Suppose we now wish to estimate the total variable costs at output levels of 7,000 and 11,000 units. For 7,000 units
TVC = 1,395.29 + 0.6351 (7,000) = 1,395.29 + 4,445.70 - 5,840.99
Using the standard error of estimate we can be confident at the 68 percent level that the actual TVC will fall within the interval of $5,840.99 plus or minus $182.02 ($5,658.97 to $6,023.01), and we can be confident at the 95 percent level that the actual TVC will fall within the interval of $5,840.99 plus or minus two standard errors of estimate ($5,476.95 to $6,205.03). Thus we can be confident at the 95 percent level that TVC will be no higher than $6,205.03, given the production of 7,000 gallons of ice cream. These confidence limits allow a best-case/worst-case scenario to be developed. Of course, a highly risk-averse decision maker may wish to extend the confidence limits to plus three standard errors of estimate in order to find the TVC below which one can be 99 percent confident that actual TVC will fall.
The estimation of TVC at 11,000 units would proceed in the same way. The result must be viewed with caution, however, because it represents an extrapolation from the data base. The regression equation applies over the range of outputs observed and hence can be applied quite confidently for 7,000 units, a case of interpolation. Outside the range of the initial observations the relationship between TVC and Q may not continue to be linear but may instead be curvilinear, exhibiting diminishing returns to the variable factors, for example. Extrapolation may be undertaken, however, if we have no good reason to expect that the relationship will not hold outside the
J Adding extra explanatory variables will inevitably explain more of the variation in the independent variable, even if the extra variables are not responsible for variation in the independent variable, since the regression analysis tends to capitalize on chance. In this present case, a cubic function of the form TVC = a + bQ + cQ 2 + dQ 1 has R 2 = 0.97642 and thus explains fractionally more of the variation in TVC, although the standard errors of the coefficients are so large that one cannot have confidence in the equation’s explanatory value. As a predictive equation, we could use the cubic expression, since the individual coefficients are not given any significance. For simplicity, we proceed with the simple linear specification with insignificant loss of accuracy.
328 Production and Cost Analysis
range of observations, as long as we are fully cognizant that the relationship may not hold. 4