Math Strategies and Tactics

5

 

Most of the questions in the two mathematics sections of the SAT are multiple-choice questions. In this chapter, you will learn the important strategies that will help you answer these questions. As a bonus, most of these tactics can also be used on the grid-in questions. However, as invaluable as these tactics are, use them only when you need them.

The first four tactics deal with the best ways of handling diagrams.

TACTIC 1.	Draw a diagram.
TACTIC 2.	If a diagram has been drawn to scale, trust it.
TACTIC 3.	If a diagram has not been drawn to scale, redraw it.
TACTIC 4.	Add a line to a diagram.

To implement these tactics, you need to be able to draw line segments and angles accurately, and also to be able to look at segments and angles and accurately estimate their measures. Let’s look at three variations of the same problem.

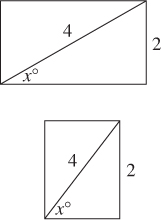
a. If the diagonal of a rectangle is twice as long as the shorter side, what is the degree measure of the angle the diagonal makes with the longer side?

b. In the rectangle at the right, what is the value of x?

c. In the rectangle at the right, what is the value of x?

NOTE

If you know how to solve a problem and are confident that you can do so accurately and reasonably quickly, JUST DO IT!

For the moment, let’s ignore the correct mathematical way to solve this problem. You should be able to look at the diagram in (b) and “see” that x is about 30, certainly between 25 and 35. In (a), however, you aren’t given a diagram, and in (c) the diagram is useless because it hasn’t been drawn to scale. In both of these cases, you should be able to draw a diagram that looks just like the one in (b); then you can look at your diagram and “see” that the measure of the angle in question is about 30°.

If this were a multiple-choice question, and the choices were as follows:

$\text{(A) 15 (B) 30 (C) 45 (D) 60}$

you would, of course, choose 30 (B). If the choices were

$\text{(A) 20 (B) 25 (C) 30 (D) 35}$

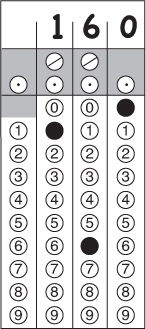
you would be a little less confident, but you should still choose 30, here (C).

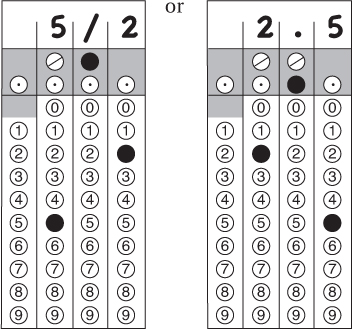
If this were a grid-in problem, you would be much less certain of your answer, but should surely bubble in 30, rather than guess a “strange” number such as 28 or 31.

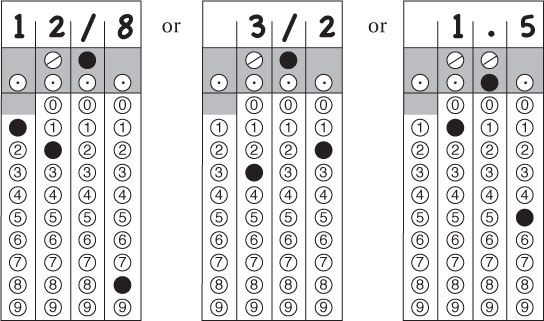
By the way, x is exactly 30. A right triangle in which one leg is half the hypotenuse must be a 30-60-90 triangle, and that leg is opposite the 30° angle [see KEY FACT J11].

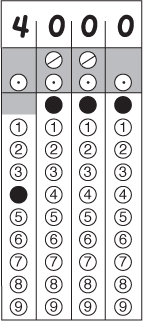
But how can you know the value of x just by looking at the diagram in (b)? In this section, you will learn not only how to look at any angle and know its measure within 5 or 10°, but also how to draw any angle with the same accuracy. You will also learn how to draw line segments of the correct lengths, so that your diagrams won’t be as bad as the one in (c). Do you see what is wrong with that diagram? The diagonal is labeled 4 and one of the sides is labeled 2, but the diagonal, as drawn, is only slightly longer than the side, not nearly twice as long.

Consider the following example:

EXAMPLE 1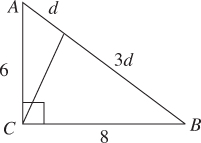

In the figure above, what is the value of d?

(A) 2

(B) 2.5

(C) 3

(D) 3.5

Solution. Since there is no note indicating that the diagram has not been drawn to scale, you can trust it [see TACTIC 2].

Clearly, d is less than AC, which is 6; but all four choices are less than 6, so that doesn’t help.

Actually, it looks as though d is less than half of AC.

So assume d < 3 and eliminate choices (C) and (D).

You could now guess between choices A and B; but if you measure, you’ll know which is right. However, there’s a problem—on the SAT, you are not allowed to use a ruler, a compass, or a protractor. So how can you measure anything? Use the back of your answer sheet!

Turn your answer sheet over, place one corner of it on point A, and with your pencil make a small mark to indicate length d. Now use this “ruler” to measure AC. Put a dot on AC d units from A; slide the answer sheet, mark off a second segment of length d, and do this once more. The third mark is well past C, so 3d is more than 6; that is, d > 2. Eliminate (A). The answer is 2.5 (B).

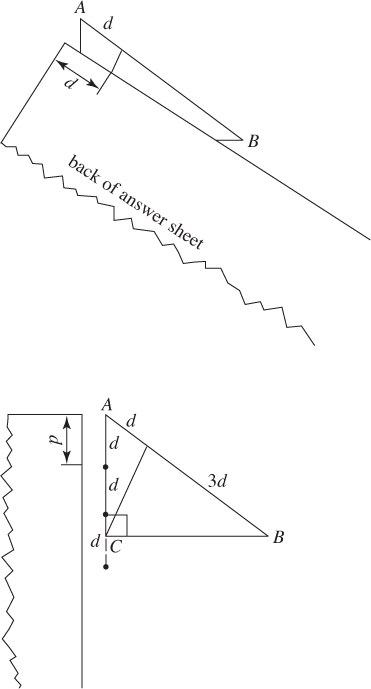
Finally, erase the dot or mark you made on the back of your answer sheet, so it won’t confuse you if you need to make a new “ruler” for another question. Also, there should be no stray pencil marks anywhere on the answer sheet when you hand it in.

To answer this question without TACTIC 2, use the Pythagorean theorem to get that

AB = 10 (or recognize that this is a 6-8-10 right triangle) and then solve the equation: d + 3d = 10 ⇒ d = 2.5.

To take full advantage of TACTICS 1, 2, and 3, you need to be able to measure angles as well as line segments. Fortunately, this is very easy. In fact, you should be able to look at any angle and know its measure within 5–10°, and be able to draw any angle accurately within 10°. Let’s see how.

First, you should easily recognize a 90° angle and can probably draw one freehand, or you can always just trace the corner of your answer sheet.

Second, to draw a 45° angle, just bisect a 90° angle. Again, you can probably do this freehand. If not, or to be more accurate, draw a right angle, mark off the same distance on each side, draw a square, and then draw in the diagonal.

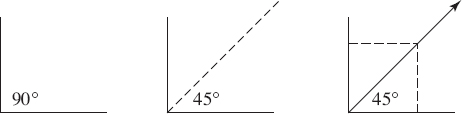
Third, to draw other acute angles, just divide the two 45° angles in the above diagram with as many lines as are necessary.

Finally, to draw an obtuse angle, add an acute angle to a right angle.

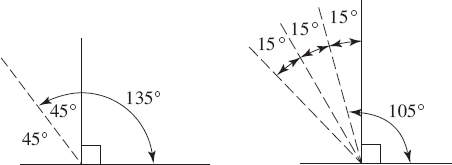
Now, to estimate the measure of a given angle, just draw in some lines.

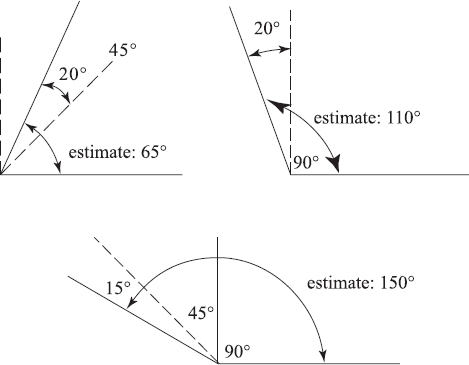
To test yourself, estimate the measure of each angle shown below. The answers that follow are written upside down.

Answers: (a) 80° (b) 20° (c) 115° (d) 160°. Did you come within 10° on each one?

TESTING TACTICS

Draw a Diagram.

On any geometry question for which a figure is not provided, draw one (as accurately as possible) in your test booklet. Drawings should not be limited, however, to geometry questions; there are many other questions on which drawings will help. Whether you intend to solve a problem directly or to use one of the tactics described in this chapter, drawing a diagram is the first step.

A good drawing requires no artistic ability. Usually, a few line segments are sufficient.

Let’s consider some examples.

EXAMPLE 2

What is the area of a rectangle whose length is twice its width and whose perimeter is equal to that of a square whose area is 1?

Solution. Don’t even think of answering this question until you have drawn a square and a rectangle and labeled each of them: each side of the square is 1; and if the width of the rectangle is w, its length (<) is 2w.

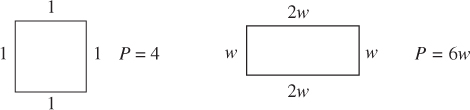
Now, write the required equation and solve it:

$6w=4\Rightarrow w=\frac{4}{6}=\frac{2}{3}\Rightarrow 2w=\frac{4}{3}$

The area of the rectangle = $\ell w=\left(\frac{4}{3}\right)\left(\frac{2}{3}\right)=\frac{8}{9}$.

Example 3

A jar contains 10 red marbles and 30 green ones. How many red marbles must be added to the jar so that 60% of the marbles will be red?

Solution. Draw a diagram and label it.

From the diagram it is clear that there are now 40 + x marbles in the jar, of which 10 + x are red. Since you want the fraction of red marbles to be 60% $\left(=\frac{3}{5}\right)$, you have $\frac{10+x}{40+x}=\frac{3}{5}$.

Cross-multiplying gives:

$\begin{array}{c}5\left(10+x\right)=3\left(40+x\right)\Rightarrow \\ 50+5x=120+3x\Rightarrow 2x=70\Rightarrow x=35\end{array}$

Of course, you could have set up the equation and solved it without the diagram, but the drawing makes the solution easier and you are less likely to make a careless mistake.

EXAMPLE 4

Tony drove 8 miles west, 6 miles north, 3 miles east, and 6 more miles north. How far was Tony from his starting place?

(A) 13

(B) 17

(C) 19

(D) 21

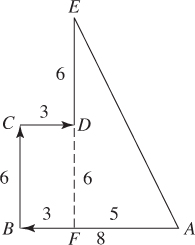
Solution. Draw a diagram. Now, extend line segment $\overline{ED}$ until it intersects $\overline{ED}$ at F [see TACTIC 4]. Then, ΔAFE is a right triangle whose legs are 5 and 12 and, therefore, its hypotenuse is 13 (A).

[If you drew the diagram accurately, you could get the right answer by measuring!]

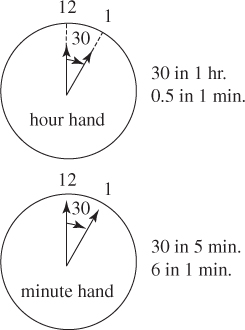
EXAMPLE 5

By how many degrees does the angle formed by the hour hand and the minute hand of a clock increase from 1:27 to 1:28?

Solution. Draw a simple picture of a clock. The hour hand makes a complete revolution, 360°, once every 12 hours. Therefore, in 1 hour it goes through 360° 12 = 30°, and in 1 minute it advances through 30° 60 = 0.5°. The minute hand moves through 30° every 5 minutes and 6° each 1 minute. Therefore, in the minute from 1:27 to 1:28 (or any other minute), the difference between the hands increases by 6 – 0.5 = 5.5 degrees. [Note that it was not necessary, and would have been more time-consuming to determine the angles between the hands at 1:27 and 1:28 (see TACTIC 10: Don’t do more than you have to).]

If a Diagram Is Drawn to Scale, Trust It, and Use Your Eyes.

Remember that every diagram that appears on the SAT has been drawn as accurately as possible unless you see “Note: Figure not drawn to scale” written below it.

For figures that are drawn to scale, the following are true: line segments that appear to be the same length are the same length; if an angle clearly looks obtuse, it is obtuse; and if one angle appears larger than another, you may assume that it is larger.

Try Examples 6 and 7, which have diagrams that have been drawn to scale. Both of these examples would be classified as hard questions. On an actual SAT, questions of comparable difficulty would be answered correctly by at most 20–35% of the students taking the exam. After you master TACTIC 2, you should have no trouble with problems like these.

EXAMPLE 6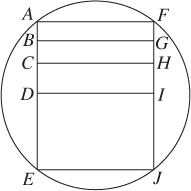

In the figure above, $\overline{ED}$, not shown, is a diagonal of rectangle AFJE and a diameter of the circle. D is the midpoint of $\overline{AE}$, C is the midpoint of $\overline{AD}$, and B is the midpoint of $\overline{AC}$.

If AE is 8 and the radius of the circle is 5, what is the area of rectangle BGHC?

(A) 4

(B) 6

(C) 8

(D) 12

Solution. Since there is no note indicating that the diagram has not been drawn to scale, you can trust it.

The area of rectangle BGHC is the product of its width, BC, and its length, BG.

AE = 8 ⇒ AD = 4 ⇒ AC = 2 ⇒ BC = 1.

$\overline{BG}$ appears to be longer than $\overline{AD}$, which is 4, and shorter than $\overline{AE}$, which is 8. Therefore, BG is more than 4 and is less than 8.

Then, the area of BGHC is more than 1 × 4 = 4 and less than 1 × 8 = 8.

The only choice between 4 and 8 is 6. The answer is (B).

Note that you never used the fact that the radius of the circle is 5, information that is necessary to actually solve the problem. You were able to answer this question merely by looking at the diagram. Were you just lucky? What if the four choices had been 4, 5, 6, and 8, so that there were two choices between 4 and 8, not just one? Well, you could have eliminated 4 and 8 and guessed, or you could have looked at the diagram even more closely. BG appears to be about the same length as CE, which is 6. If BG is 6, then the area of BGHC is exactly 6. How can you be sure? Measure the lengths!

On the answer sheet make two small pencil marks to indicate length BG:

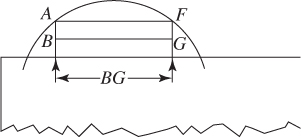
Now, use that length to measure CE:

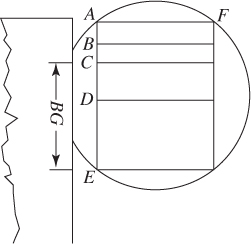
The lengths are the same. BG is 6; the area is 6. It’s not a guess after all.

Mathematical Solution. Diameter $\overline{EF}$, which is 10, is also the hypotenuse of right triangle EAF. Since leg $\overline{AE}$ is 8, $\overline{AF}$, the other leg, is 6 (either you recognize this as a 6-8-10 triangle, or you use the Pythagorean theorem). Since BG = AF, BG is 6, and the area is 6.

 

If Example 6 had been a grid-in problem instead of a multiple-choice question, you could have used TACTIC 2 in exactly the same way, but you would have been less sure of your answer. If, based on a diagram, you know that the area of a rectangle is about 6 or the measure of an angle is about 30°, you can almost always pick the correct choice, but on a grid-in you can’t be certain that the area isn’t 6.2 or the angle 31°. Nevertheless, if you can’t solve a problem directly, you should always grid in a “simple” number that is consistent with the diagram.

Now try using TACTIC 2 on Examples 7 and 8.

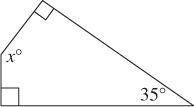
EXAMPLE 7

In the figure to the right, what is the value of x?

(A) 95

(B) 125

(C) 135

(D) 145

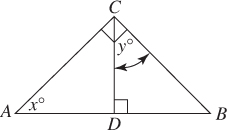
EXAMPLE 8

In the figure to the right, what is the value of x – y?

(A) –15

(B) 0

(C) 15

(D) 30

Solution 7 Using TACTIC 2. Since the diagram is drawn to scale, trust it. Look at x: it appears to be about 90 + 50 = 140. In this case, using TACTIC 2 did not get you the exact answer. It only enabled you to narrow down the choices to (C) and (D). At this point, you would guess—unless, of course, you know the following mathematical solution.

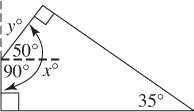
Mathematical Solution 7. The sum of the measures of the four angles in any quadrilateral is 360° (KEY FACT K1). Then

$\begin{array}{cc}360=90+90+35+x=215+x\Rightarrow x=360-215=145& \left(D\right)\end{array}$

 

Solution 8 Using TACTIC 2. In the diagram, x and y look about the same, so assume they are. Certainly, neither one is 30° or even 15° greater than the other. Therefore, x – y = 0 (C)

Mathematical Solution 8. The sums of the measures of the three angles in triangles ABC and CBD are equal (they are both 180°). Then

$\begin{array}{cc}90+\text{m}\angle B+x=90+\text{m}\angle B+y\Rightarrow x=y\Rightarrow x-y=0& \left(B\right)\end{array}$

 

Now try Examples 9–11, in which the diagrams are drawn to scale, and you need to find the measures of angles. Even if you know that you can solve these problems directly, practice TACTIC 2 and estimate the answers. The correct mathematical solutions without using this tactic are also given.

EXAMPLE 9

If, in the figure above, AB = AC, what is the value of x?

(A) 135

(B) 125

(C) 115

(D) 65

Solution Using TACTIC 2. Ignore the information in the question. Just “measure” x. Draw DC perpendicular to AB, and let EC divide right angle DCA into two 45° angles, ∠DCE and ∠ACE.

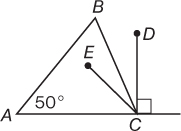
Now, ∠DCB is about half of ∠DCE, say 20–25°. Therefore, your estimate for x should be about 110 (90 + 20) or 115 (90 + 25). Choose (C).

Mathematical Solution. Since ΔABC is isosceles, with AB = AC, the other two angles in the triangle, ∠B and ∠C, each measure 65°. Therefore,

$x+65=180\Rightarrow x=115$

EXAMPLE 10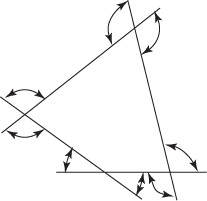

In the figure above, what is the sum of the measures of all of the marked angles?

(A) 360°

(B) 540°

(C) 720°

(D) 900°

Solution Using TACTIC 2. Make your best estimate of each angle, and add up the values. The four choices are so far apart that, even if you’re off by 15° or more on some of the angles, you’ll get the right answer. The sum of the estimates shown below is 690°, so the correct answer must be 720° (C).

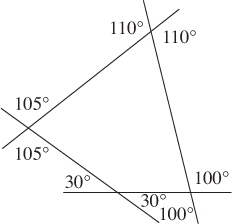
Mathematical Solution. Each of the eight marked angles is an exterior angle of the quadrilateral. If we take one angle from each pair, their sum is 360° (KEY FACT K3); so, taking both angles at each vertex, we find that the sum of the measures is 360° + 360° = 720°.

EXAMPLE 11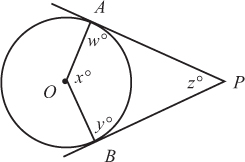

In the diagram above, rays $\overrightarrow{PA}$ and $\overrightarrow{PB}$ are tangent to circle O. Which of the following is equal to z?

(A) x

(B) 180 – x

(C) w + x + y

(D) $\frac{w+x+y}{3}$

Solution Using TACTIC 2. The diagram is drawn to scale, so trust it. In the figure, x is clearly greater than 90 and z is clearly less than 90, so choices (A) and (C) are surely wrong. Also, it appears that w and y are each about 90, so w + x + y is more than 270. So choice (D) is greater than $\frac{270}{3}=90$ and could not be equal to z.

The answer must be (B).

HELPFUL HINT

In order to redraw a diagram to scale, you first have to ask yourself, “What is wrong with the original diagram?” If an angle is marked 45°, but in the figure it looks like a 75° angle, redraw it. If two line segments appear to be parallel, but you have not been told that they are, redraw them so that they are clearly not parallel. If two segments appear to have the same length, but one is marked 5 and the other 10, redraw them so that the second segment is twice as long as the first.

Mathematical Solution. Tangents to a circle are perpendicular to the radii drawn to the points of contact, so w and y both equal 90. The sum of the four angles in a quadrilateral is 360°, so w + x + y + z = 360. Then 90 + x + 90 + z = 360 ⇒ x + z = 180 ⇒ z = 180 – x (B) .

If a Diagram Is Not Drawn to Scale, Redraw It to Scale, and Then Use Your Eyes.

For figures that have not been drawn to scale, you can make no assumptions. Lines that look parallel may not be; an angle that appears to be obtuse may, in fact, be acute; two line segments may have the same length even though one looks twice as long as the other.

In the examples illustrating TACTIC 2, all of the diagrams were drawn to scale and could be used to advantage. When diagrams have not been drawn to scale, you must be much more careful. TACTIC 3 tells you to redraw the diagram as accurately as possible, based on the information you are given, and then to apply the technique of TACTIC 2.

CAUTION: Redrawing a diagram, even roughly, takes time. Do this only when you do not see an easy direct solution to the problem.

EXAMPLE 12

In ΔACB, what is the value of x?

Note: Figure not drawn to scale

(A) 75

(B) 60

(C) 45

(D) 30

HELPFUL HINT

Even if a diagram is not drawn to scale, any angle with a small square in it must be a right angle.

Solution. In what way is this figure not drawn to scale? AB = 8 and BC = 4, but in the figure $\overline{BC}$ is not twice as long as $\overline{BC}$. Redraw the triangle so that $\overline{AB}$ is twice as long as $\overline{BC}$. Be sure to draw a right triangle. Even though the figure is not drawn to scale, the little square in angle C guarantees it is a right angle.

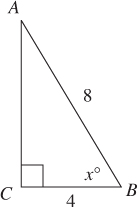
Now, just look: x is about 60 (B).

Mathematical Solution. In fact, x is exactly 60. If the hypotenuse of a right triangle is twice the length of one of the legs, the triangle is a 30-60-90 triangle, and the angle formed by the hypotenuse and that leg is 60° (see Section 6-J).

EXAMPLE 13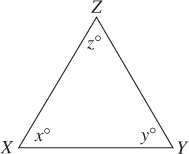

Note: Figure not drawn to scale

In ΔXYZ at the right, if XY < YZ < ZX, then which of the following must be true?

(A) x < 60

(B) z < 60

(C) y < z

(D) x < z

Solution. As drawn, the diagram is useless. The triangle looks like an equilateral triangle, even though the question states that XY < YZ < ZX. Redraw the figure so that the condition is satisfied (that is, $\overline{ZX}$ is clearly the longest side and $\overline{XY}$ the shortest).

From the redrawn figure, it is clear that y is the largest angle (eliminate choice (C)) and z < x (eliminate (D) as well). Both x and z appear to be less than 60, but only one answer can be correct. Since z< x, if only one of these angles is less than 60, it must be z. Therefore, z < 60 (B) must be true.

EXAMPLE 14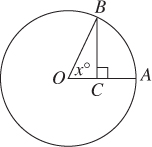

Note: Figure not drawn to scale

In the figure above, O is the center of the circle. If OA = 4 and BC = 2, what is the value of x?

(A) 15

(B) 30

(C) 45

(D) 60

Solution Using TACTIC 3. Do you see why the figure isn’t drawn to scale? $\overline{BC}$, which is 2, looks almost as long as $\overline{OA}$, which is 4. Redraw the diagram, making sure that $\overline{BC}$ is only one-half as long as $\overline{OA}$. With the diagram drawn to scale, you can see that x is approximately 30 (C).

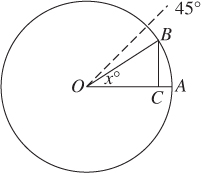
Mathematical Solution. Since $\overline{OB}$ is a radius, it has the same length as radius $\overline{OA}$, which is 4. Then ΔBCO is a right triangle in which the hypotenuse is twice as long as one leg. This can occur only in a 30-60-90 triangle, and the angle opposite that leg measures 30°. Therefore, x = 30.

Add a Line to a Diagram.

Occasionally, after staring at a diagram, you still have no idea how to solve the problem to which it applies. It looks as though there isn’t enough given information. In this case, it often helps to draw another line in the diagram.

EXAMPLE 15

In the figure to the right, Q is a point on the circle whose center is O and whose radius is r, and OPQR is a rectangle. What is the length of diagonal PR?

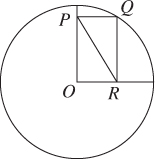
(A) r

(B) r²

(C) $\frac{r^2}{\pi }$

(D) $\frac{r\sqrt{2}}{\pi }$

Solution. If, after staring at the diagram and thinking about rectangles, circles, and the Pythagorean theorem, you’re still lost, don’t give up. Ask yourself, “Can I add another line to this diagram?” As soon as you think to draw in $\overline{OQ}$, the other diagonal, the problem becomes easy. In a rectangle, the two diagonals are congruent. Since $\overline{OQ}$ is a radius, OQ = PR = r (A) .

Test the Choices, Starting with (B) or (C).

TACTIC 5, often called backsolving, is useful when you are asked to solve for an unknown and you understand what needs to be done to answer the question, but you want to avoid doing the algebra. The idea is simple: test the various choices to see which one is correct.

Note: On the SAT the answers to virtually all numerical multiple-choice questions are listed in either increasing or decreasing order. Consequently, (B) and (C) are the middle values; and in applying TACTIC 5, you should always start with one of them. For example, assume that choices (A), (B), (C), and (D) are given in increasing order. Try (C). If it works, you’ve found the answer. If C doesn’t work, you should now know whether you need to test a larger number or a smaller one, and that information permits you to eliminate one or two more choices. If (C) is too small, you need a larger number, so (A) and (B) are out; the answer is (D). If (C) is too large, you can eliminate (D), which is even larger.

Example 16 illustrates the proper use of TACTIC 5.

EXAMPLE 16

If the average (arithmetic mean) of 2, 7, and x is 12, what is the value of x?

(A) 9

(B) 12

(C) 21

(D) 27

Solution. Use TACTIC 5. Test choice (C): x = 21.

Is the average of 2, 7, and 21 equal to 12?

No: $\frac{2+7+21}{3}=\frac{30}{3}=10$, which is too small.

Eliminate (C); also, since, for the average to be 12, x must be greater than 21, eliminate (A) and (B).

The answer is (D).

 

Every problem that can be solved using TACTIC 5 can be solved directly, often in less time. Therefore, we stress: if you are confident that you can solve a problem quickly and accurately, just do so.

Here is the direct method for solving Example 16, which is faster than backsolving. (See Section 9-E on averages.) If you know this method, you should use it and save TACTIC 5 for problems that you can’t easily solve directly.

Direct Solution. If the average of three numbers is 12, their sum is 36. Then

$2+7+x=36\Rightarrow 9+x=36\Rightarrow x=27$

 

Some tactics allow you to eliminate one or two choices so that you can make an educated guess. On problems where TACTIC 5 can be used, it always leads you to the right answer. The only reason not to use it on a particular problem is that you can easily solve the problem directly.

Now try applying TACTIC 5 to Examples 17 and 18.

EXAMPLE 17

If the sum of five consecutive even integers is 740, what is the largest of these integers?

(A) 156

(B) 152

(C) 146

(D) 144

Solution. Use TACTIC 5. Test choice (C): 146.

If 146 is the largest of the five integers, the integers are 146, 144, 142, 140, and 138. Quickly add them on your calculator. The sum is 710.

Since 710 is too small, eliminate (C) and (D).

If you noticed that the amount by which 710 is too small is 30, you should realize that each of the five numbers needs to be increased by 6; therefore, the largest is 152 (B).

If you didn’t notice, just try 152, and see that it works.

This solution is easy, and it avoids having to set up and solve the required equation:

n + (n + 2) + (n + 4) + (n + 6) + (n + 8) = 740

EXAMPLE 18

A competition offers a total of $250,000 in prize money to be shared by the top three contestants. If the money is to be divided among them in the ratio of 1:3:6, what is the value of the largest prize?

(A) $ 25,000

(B) $ 75,000

(C) $100,000

(D) $150,000

Solution. Use TACTIC 5. Test choice (C): $100,000.

If the largest prize were $100,000, the second largest would be $50,000 (they are in the ratio of 6:3 = 2:1). The third prize would be much less than $50,000, so all three would add up to less than $200,000.

Eliminate (A), (B), and (C).

The answer is (D).

Again, TACTIC 5 lets you avoid the algebra if you can’t do it or just don’t want to. Here is the correct solution. By TACTIC D1 the three prizes are x, 3x, and 6x. Therefore,

$x+3x+6x=\$250,000\Rightarrow 10x=\$250,000$

So, x = $25,000 and 6x = $150,000.

EXAMPLE 19

If $2\sqrt{2x+1}+5+8$, then x =

(A) $-\frac{1}{8}$

(B) 0

(C) $\frac{5}{8}$

(D) 1

Solution. Since plugging in 0 is much easier than plugging in $\frac{5}{8}$, start with B. If x = 0, the left-hand side of the equation is $2\sqrt{1}+5$, which is equal to 7 and so is too small. Eliminate (A) and (B), and try something bigger. Still preferring whole numbers to fractions, try choice (D). If x = 1, then $2\sqrt{2\left(1\right)+1}+5=2\sqrt{3}+5\approx 8.46$.

Since that’s too big, eliminate (D). The answer must be (C) $\frac{5}{8}$.

Again, remember: no matter what the choices are, backsolve only if you can’t easily do the algebra. Many students would do this problem directly:

$2\sqrt{2x+1}+5=8\Rightarrow 2\sqrt{2x+1}=3\Rightarrow \sqrt{2x+1}=\frac{3}{2}.$

So, $2x+1={\left(\frac{3}{2}\right)}^2=\frac{9}{4}\Rightarrow 2x=\frac{5}{4}\Rightarrow x=\frac{5}{8}$ and save backsolving for an even harder problem.

You have to determine which method is better for you.

 

For some multiple-choice questions on the SAT, you have to test the various choices. On these problems you are not really backsolving (there is nothing to solve!); rather, you are testing whether a particular choice satisfies a given condition.

Examples 20 and 21 are two such problems. In Example 20, you are asked for the largest integer that satisfies a certain condition. Usually, some of the smaller integers offered as choices also satisfy the condition, but your job is to find the largest one.

EXAMPLE 20

What is the largest integer, n, such that $\frac{112}{2^n}$ is an integer?

(A) 2

(B) 3

(C) 4

(D) 5

Solution. Since you want the largest value of n for which $\frac{112}{2^n}$ is an integer, start by testing 5, choice D, the largest of the choices.

Is $\frac{112}{2^5}$ an integer? No: $\frac{112}{2^5}=\frac{112}{32}=3.5$.

Eliminate (D) and try (C).

Is $\frac{112}{2^4}$ an integer? Yes: 2⁴ = 16, and $\frac{112}{16}=7$.

The answer is 4 (C).

It doesn’t matter whether any of the smaller choices work (you need the largest), although in this case, they both do.

 

Surprisingly, on a problem that asks for the smallest number satisfying a property, you should also start with (D), because the choices for these problems are usually given in decreasing order.

It is also better to start with (D) on questions such as Example 21, in which you are asked “which of the following...?” The right answer is rarely one of the first choices.

Sometimes a question asks which of the four choices satisfies a certain condition. Usually, in this situation there is no way to answer the question directly. Rather, you must look at the choices and test each of them until you find one that works. At that point, stop—none of the other choices could be correct. There is no particular order in which to test the choices, but it makes sense to test the easier ones first. For example, it is usually easier to test whole numbers than fractions and positive numbers than negative ones.

EXAMPLE 21

Which of the following is NOT equivalent to $\frac{3}{5}$?

(A) 60%

(B) 0.6

(C) $\frac{3}{7}\times \frac{7}{5}$

(D) $\frac{3}{7}÷\frac{7}{5}$

Solution. Here, you have to test each of the choices until you find one that satisfies the condition that it is not equal to $\frac{3}{5}$. If, as you glance at the choices to see if any would be easier to test than the others, you happen to notice that 60% = 0.6, then you can immediately eliminate choices (A) and (B), since it is impossible that both are correct.

Test choice (C). $\frac{3}{7}\times \frac{7}{5}=\frac{3}{5}$.

You now know that (D) must be the correct answer. In fact, $\frac{3}{7}÷\frac{7}{5}=\frac{3}{7}\times \frac{5}{7}=\frac{15}{49}\ne \frac{3}{5}$.

Replace Variables with Numbers.

Mastery of TACTIC 6 is critical for anyone developing good test-taking skills. This tactic can be used whenever the four choices in a multiple-choice math question involve the variables in the question. There are three steps:

1. Replace each variable with an easy-to-use number.

2. Solve the problem using those numbers.

3. Evaluate each of the four choices with the numbers you picked to see which choice is equal to the answer you obtained.

Examples 22 and 23 illustrate the proper use of TACTIC 6.

EXAMPLE 22

If a is equal to b multiplied by c, which of the following is equal to b divided by c ?

(A) $\frac{a}{bc}$

(B) $\frac{\mathrm{ab}}{c}$

(C) $\frac{a}{c}$

(D) $\frac{a}{c^2}$

Solution.

Pick three easy-to-use numbers that satisfy a = bc: for example, a = 6, b = 2, c = 3.

Solve the problem with these numbers: $b÷c=\frac{b}{c}=\frac{2}{3}$.

Check each of the four choices to see which one is equal to $\frac{2}{3}$:

(A) $\frac{a}{bc}=\frac{6}{\left(2\right)\left(3\right)}=1:\text{NO}$

(B) $\frac{ab}{c}=\frac{\left(6\right){\left(3\right)}^1}{3_1}=6:\text{NO}$

(C) $\frac{a}{c}=\frac{6}{3}=2:\text{NO.}$

(D) $\frac{a}{c^2}=\frac{6}{3^2}=\frac{6}{9}=\frac{2}{3}:\text{YES!}$

The answer is (D).

EXAMPLE 23

If the sum of four consecutive odd integers is s, then, in terms of s, what is the greatest of these integers?

(A) $\frac{s-12}{4}$

(B) $\frac{s-6}{4}$

(C) $\frac{s+6}{4}$

(D) $\frac{s+12}{4}$

Solution.

Pick four easy-to-use consecutive odd integers: say, 1, 3, 5, 7. Then s, their sum, is 16.

Solve the problem with these numbers: the greatest of these integers is 7.

When s = 16, the four choices are, $\frac{s-12}{4}=\frac{4}{4},\frac{s-6}{4}=\frac{10}{4},\frac{s+6}{4}=\frac{22}{4}$ and $\frac{s+12}{4}=\frac{28}{4}$.

Only $\frac{28}{4}$, choice (D), is equal to 7.

 

Of course, Examples 22 and 23 can be solved without using TACTIC 6 if your algebra skills are good. Here are the solutions.

Solution 22. $a=bc\Rightarrow b=\frac{a}{c}\Rightarrow b÷c=\frac{a}{c}÷c=\frac{a}{c^2}$.

Solution 23. Let n, n + 2, n + 4, and n + 6 be four consecutive odd integers, and let s be their sum. Then:

$s=n+\left(n+2\right)+\left(n+4\right)+\left(n+6\right)=4n+12$

Therefore:

$n=\frac{s-12}{4}\Rightarrow n+6=\frac{s-12}{4}+6=\frac{s-12}{4}+\frac{24}{4}=\frac{s+12}{4}$

 

The important point is that, if you are uncomfortable with the correct algebraic solution, you can use TACTIC 6 and always get the right answer. Of course, even if you can do the algebra, you should use TACTIC 6 if you think you can solve the problem faster or will be less likely to make a mistake. With the proper use of the tactics in this chapter, you can correctly answer many problems that you may not know how to solve mathematically.

Example 24 is somewhat different. You are asked to reason through a word problem involving only variables. Many students find problems like these mind-boggling. Here, the use of TACTIC 6 is essential.

HELPFUL HINT

Replace the variables with numbers that are easy to use, not necessarily ones that make sense. It is perfectly OK to ignore reality. A school can have five students, apples can cost $10 each, trains can go 5 miles per hour or 1000 miles per hour—it doesn’t matter.

EXAMPLE 24

If a school cafeteria needs c cans of soup each week for each student, and if there are s students in the school, for how many weeks will x cans of soup last?

(A) $\frac{cx}{s}$

(B) $\frac{xs}{c}$

(C) $\frac{s}{cx}$

(D) $\frac{x}{cs}$

Solution.

Replace c, s, and x with three easy-to-use numbers. If a school cafeteria needs 2 cans of soup each week for each student, and if there are 5 students in the school, how many weeks will 20 cans of soup last?

Since the cafeteria needs 2 × 5 = 10 cans of soup per week, 20 cans will last for 2 weeks.

Which of the choices equals 2 when c = 2, s = 5, and x = 20?

The four choices become: $\frac{cx}{s}=8$, $\frac{xs}{c}=50$, $\frac{s}{cx}=\frac{1}{8}$, $\frac{x}{cs}=2$.

The answer is (D).

 

Even though Example 24 is more abstract than Examples 22 and 23, it too can be solved directly and more quickly if you can manipulate the variables.

Algebraic Solution 24. If each week the school needs c cans for each of the s students, then it will need cs cans per week. Dividing cs into x gives the number of weeks that x cans will last: $\frac{x}{cs}$.

 

Now, practice TACTIC 6 on the following problems.

EXAMPLE 25

Nadia will be x years old y years from now. How old was she z years ago?

(A) x + y + z

(B) x + y – z

(C) x – y – z

(D) y – x – z

EXAMPLE 26

If $a=b+\frac{1}{2},b=2c+\frac{1}{2}$, and $c=3d+\frac{1}{2}$, which of the following is an expression for d in terms of a?

(A) $\frac{a-2}{6}$

(B) $\frac{2a-3}{6}$

(C) $\frac{2a-3}{12}$

(D) $\frac{3a-2}{18}$

EXAMPLE 27

Anne drove for h hours at a constant rate of r miles per hour. How many miles did she go during the final 20 minutes of her drive?

(A) $\frac{hr}{3}$

(B) 3rh

(C) $\frac{hr}{20}$

(D) $\frac{r}{3}$

Solution 25. Assume Nadia will be 10 in 2 years. How old was she 3 years ago? If she will be 10 in 2 years, she is 8 now and 3 years ago was 5. Which of the choices equals 5 when x = 10, y = 2, and z = 3? Only x – y – z (C) .

Solution 26. Let d = 1. Then $c=3\frac{1}{2}$, $b=7\frac{1}{2}$, and a = 8. Which of the choices equals 1 when a = 8? Only $\frac{a-2}{6}(A)$.

Solution 27. If Anne drove at 60 miles per hour for 2 hours, how far did she go in the last 20 minutes?

Since 20 minutes is $\frac{1}{3}$ of an hour, she went $20\left(\frac{1}{2}\text{ of }60\right)$ miles.

Only $\frac{r}{3}\left(D\right)=20$ when r = 60 and h = 2.

Notice that h is irrelevant. Whether Anne had been driving for 2 hours or 20 hours, the distance she covered in her last 20 minutes would be the same.

Choose an Appropriate Number.

TACTIC 7 is similar to TACTIC 6 in that you pick a convenient number. However, here no variable is given in the problem. TACTIC 7 is especially useful in problems involving fractions, ratios, and percents.

EXAMPLE 28

At Central High School, each student studies exactly one foreign language. Three-fifths of the students take Spanish, and one-fourth of the remaining students take Italian. If all of the others take French, what percent of the students take French?

(A) 15

(B) 20

(C) 25

(D) 30

HELPFUL HINT

In problems involving fractions, the best number to use is the least common denominator of all the fractions. In problems involving percents, the easiest number to use is 100. (See Sections 6-B and 6-C.)

Solution. The least common denominator of $\frac{3}{5}$ and $\frac{3}{5}$ is 20, so assume that there are 20 students at Central High. (Remember that the number you choose doesn’t have to be realistic.) Then the number of students taking Spanish is $12\left(\frac{3}{5}\text{ of }20\right)$. Of the remaining 8 students, $2\left(\frac{1}{4}\text{ of }8\right)$ take Italian. The other 6 take French. Finally, 6 is 30% of 20.

The answer is (D).

EXAMPLE 29

From 2013 to 2014, the number of boys in the school chess club decreased by 20%, and the number of girls in the club increased by 20%. The ratio of girls to boys in the club in 2014 was how many times the ratio of girls to boys in the club in 2013?

(A) $\frac{2}{3}$

(B) $\frac{4}{5}$

(C) $\frac{5}{4}$

(D) $\frac{3}{2}$

Solution. This problem involves percents, so try to use 100. Assume that in 2013 there were 100 boys and 100 girls in the club. Since 20% of 100 is 20, in 2014 there were 120 girls (a 20% increase) and 80 boys (a 20% decrease). See the following chart:

Year	Number of Girls	Number of Boys	Ratio of Girls to Boys
2013	100	100	$\frac{100}{100}=1$
2014	120	80	$\frac{120}{80}=\frac{3}{2}$

The chart shows that the 2013 ratio of 1 was multiplied by $\frac{3}{2}$. The answer is(D) .

 

Here are two more problems where TACTIC 7 is useful.

EXAMPLE 30

In a particular triathlon the athletes cover $\frac{1}{24}$ of the total distance by swimming, $\frac{1}{3}$ of it by running, and the rest by bike. What is the ratio of the distance covered by bike to the distance covered by running?

(A) 15:8

(B) 8:5

(C) 5:8

(D) 8:15

EXAMPLE 31

From 2012 to 2013 the sales of a book decreased by 80%. If the sales in 2014 were the same as in 2012, by what percent did they increase from 2013 to 2014?

(A) 100%

(B) 120%

(C) 400%

(D) 500%

Solution 30. The least common denominator of the two fractions is 24, so assume that the total distance is 24 miles. Then, the athletes swim for 1 mile and run for $8\left(\frac{1}{3}\text{of}24\right)$ miles. The

remaining 15 miles they cover by bike. Therefore, the required ratio is 15:8 (A).

Solution 31. Use TACTIC 7, and assume that 100 copies were sold in 2012 (and 2014). Sales dropped by 80 (80% of 100) to 20 in 2013 and then increased by 80, from 20 back to 100, in 2014. The percent increase was

$\frac{\text{actual increase}}{\text{originalamount}}\times 100\%=\frac{80}{20}\times 100\%=400\%(C)$

Eliminate Absurd Choices, and Guess.

Of course, whenever you have no idea how to solve a problem, you guess. First be sure to eliminate all the absurd choices.

During the course of an SAT, you will probably find at least a few multiple-choice questions that you have no idea how to solve. Before taking a wild guess look at the choices. Often one or two of the answers are absurd. Eliminate them and then guess. Occasionally, three of the choices are absurd. When this occurs, your answer is no longer a guess!

What makes a choice absurd? Lots of things. Even if you don’t know how to solve a problem, even with very hard ones, you may realize that:

the answer must be positive, but some of the choices are negative;

the answer must be even, but some of the choices are odd;

the answer must be less than 100, but some choices exceed 100;

a ratio must be less than 1, but some choices are greater than or equal to 1.

Let’s look at several examples. In a few of them the information given is intentionally insufficient to solve the problem, but you will still be able to determine that some of the answers are absurd. In each case the “solution” provided will indicate which choices you should have eliminated. At that point you would simply guess. Remember: on the SAT when you decide to guess, don’t agonize. Just make your choice and then move on.

Example 32

A region inside a semicircle of radius r is shaded. What is the area of the shaded region?

(A) $\frac{1}{4}\pi r^2$

(B) $\frac{1}{3}\pi r^2$

(C) $\frac{1}{2}\pi r^2$

(D) $\frac{2}{3}\pi r^2$

Solution. You may have no idea how to find the area of the shaded region, but you should know that, since the area of a circle is r², the area of a semicircle is $\frac{1}{2}\pi r^2$. Therefore, the area of the shaded region must be less than $\frac{1}{2}\pi r^2$, so eliminate (C) and (D). On an actual problem that includes a diagram, if the diagram is drawn to scale, you may be able to make an educated guess between (A) and (B). If not, just choose one or the other.

Example 33

The average of 5, 10, 15, and x is 20. What is x?

(A) 20

(B) 25

(C) 45

(D) 50

Solution. If the average of four numbers is 20, and three of them are less than 20, the other one must be greater than 20. Eliminate (A). If you further realize that, since 5 and 10 are a lot less than 20, x will probably be a lot more than 20, eliminate (B), as well. Then guess either (C) or (D).

Example 34

If 25% of 220 equals 5.5% of w, what is w?

(A) 55

(B) 100

(C) 110

(D) 1000

Solution. Since 5.5% of w equals 25% of 220, which is surely greater than 5.5% of 220, w must be greater than 220. Eliminate (A), (B), and (C)! The answer must be (D)!

Example 34 illustrates an important point. Even if you know how to solve a problem, if you immediately see that three of the four choices are absurd, just pick the remaining choice and move on.

Example 35

A prize of $27,000 is to be divided in some ratio among three people. What is the largest share?

(A) $18,900

(B) $13,500

(C) $ 8100

(D) $ 5400

Solution. If the prize were divided equally, each share would be worth $9000. If it is divided unequally, the largest share is surely more than $9000, so eliminate (C) and (D). In an actual question, you would be told what the ratio is, and that information should enable you to eliminate (A) or (B). If not, you would just guess.

Example 36

A jar contains only red and blue marbles. The ratio of the number of red marbles to the number of blue marbles is 5:3. What percent of the marbles are blue?

(A) 37.5%

(B) 50%

(C) 60%

(D) 62.5%

Solution. Since there are 5 red marbles for every 3 blue ones, there are fewer blue ones than red ones. Therefore, fewer than half (50%) of the marbles are blue. Eliminate (B), (C), and (D). The answer is (A).

Now use TACTIC 8 on each of the following problems. Even if you know how to solve them, don’t. Practice this technique, and see how many choices you can eliminate without actually solving.

Example 37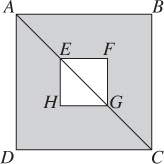

Note: Figure not drawn to scale

In the figure above, diagonal $\overline{EG}$ of square EFGH is one-half of diagonal $\overline{AC}$ of square ABCD. What is the ratio of the area of the shaded region to the area of ABCD?

(A) $\sqrt{2}:1$

(B) 3:4

(C) $\sqrt{2}:2$

(D) 1:2

Example 38

Jim receives a commission of 25¢ for every $20.00 worth of merchandise he sells. What percent is his commission?

(A) $1\frac{1}{4}\%$

(B) $2\frac{1}{2}\%$

(C) 5%

(D) 25%

Example 39

From 2000 to 2010, Michael’s weight increased by 25%. If his weight was W kilograms in 2010, what was it in 2000?

(A) 1.25 W

(B) 1.20 W

(C) .80 W

(D) .75 W

Example 40

The average of 10 numbers is −10. If the sum of six of them is 100, what is the average of the other four?

(A) −100

(B) −50

(C) 50

(D) 100

Example 41

What is 3% of 4%?

(A) 0.12%

(B) 1.2%

(C) 7%

(D) 12%

Example 42

If f(x) = 4x² + 2x⁴, what is the value of f(−2)?

(A) −48

(B) −32

(C) 0

(D) 48

Solution 37. Obviously, the shaded region is smaller than square ABCD, so the ratio must be less than 1. Eliminate (A) $(\sqrt{2}>1.4)$. Also, from the diagram, it is clear that the shaded region is more than half of square ABCD, so the ratio is greater than 0.5. Eliminate (D). Since 3:4 = 0.75 and $\sqrt{2}:2\approx 0.71$, (B) and (C) are too close to tell which is right just by looking. So guess. The answer is (B).

Solution 38. Clearly, a commission of 25¢ on $20 is quite small. Eliminate (D), and guess one of the small percents. If you realize that 1% of $20 is 20¢, then you know the answer is a little more than 1%, and you should guess (A) (maybe (B), but definitely not (C)). The answer is (A).

Solution 39. Since Michael’s weight increased, his weight in 2000 was less than W. Eliminate (A) and (B), and guess. The answer is (C).

Solution 40. Since the average of all 10 numbers is negative, so is their sum. However, the sum of the first six is positive, so the sum (and the average) of the others must be negative. Eliminate (C) and (D). The answer is (B).

Solution 41. Since 3% of a number is just a small part of it, 3% of 4% must be much less than 4%. Eliminate (C) and (D), and probably (B). The answer is (A).

Solution 42. Any nonzero number raised to an even power is positive, so 4x² + 2x⁴ is positive. Eliminate (A), (B), and (C). The answer is (D).

Subtract to Find Shaded Regions.

Whenever part of a figure is white and part is shaded, the straightforward way to find the area of the shaded portion is to find the area of the entire figure and then subtract from it the area of the white region. Of course, if you are asked for the area of the white region, you can, instead, subtract the shaded area from the total area. Occasionally, you may see an easy way to calculate the shaded area directly, but usually you should subtract.

Example 43

In the figure above, ABCD is a rectangle, and $\stackrel{⌢}{BE}$ and$\stackrel{⌢}{CF}$ are arcs of circles centered at A and D. What is the area of the shaded region?

(A) 10 − π

(B) 2(5 − π)

(C) 2(5 − 2π)

(D) 6 + 2π

Solution. The entire region is a 2 × 5 rectangle whose area is 10. Since each white region is a quarter-circle of radius 2, the combined area of these regions is that of a semicircle of radius $2:\frac{1}{2}\pi {\left(2\right)}^2=2\pi$. Therefore, the area of the shaded region is 10 − 2π = 2(5 − π) (B).

The idea of subtracting a part from the whole works with line segments as well as areas.

Example 44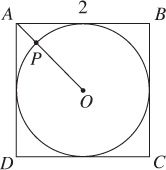

In the figure above, the circle with center O is inscribed in square ABCD. Line segment $\overline{AO}$ intersects the circle at P. What is the length of $\overline{AP}$?

(A) $2-\sqrt{2}$

(B) $1-\frac{\sqrt{2}}{2}$

(C) $2\sqrt{2}-2$

(D) $\sqrt{2}-1$

Solution. First use TACTIC 4 and draw some lines. Extend $\overline{AO}$ to form diagonal $\overline{AC}$.

Then, since ΔADC is an isosceles right triangle, $AC=2\sqrt{2}$ (KEY FACT J8) and AO is half of that, or $\sqrt{2}$. Then draw in diameter $\overline{EF}$ parallel to $\overline{AD}$. Since the diameter is 2 (EF = AD = 2), the radius is 1. Finally, subtract: $AP=AO-PO=\sqrt{2}-1\left(D\right)$.

Note: If you don’t realize which lines to add and/or you can’t reason a question like this one out, you can still make an educated guess. Use TACTIC 2: trust the diagram. Since AB = 2, then AE = 1, and AP is less than 0.5.

With your calculator evaluate each choice. (A) and (C) are both greater than 0.5. Eliminate them, and guess either (B) or (D). Since choice (B) is a lot less than 0.5, (D) is the better guess.

Don’t Do More Than You Have To.

In Example 5 on page 385, you were asked, “By how many degrees does the angle formed by the hour hand and the minute hand of a clock increase from 1:27 to 1:28?” If you look at the solution, you will see that we didn’t have to calculate either angle. This is a common situation. Look for shortcuts. Since a problem can often be solved in more than one way, you should always look for the easiest method. Consider the following examples.

Example 45

If 5(3x − 7) = 20, what is 3x− 8?

It’s not difficult to solve for x:

$\begin{array}{c}5\left(3x-7\right)=20\Rightarrow 15x-35=20\Rightarrow 15x=55\Rightarrow \\ x=\frac{55}{15}=\frac{11}{3}\end{array}$

But it’s too much work. Besides, once you find that $x=\frac{11}{3}$, you still have to multiply to get $3x:3\left(\frac{11}{3}\right)=11$, and then subtract to get 3x − 8: 11 − 8 = 3.

Solution. The key is to recognize that you don’t need x. Finding 3x − 7 is easy (just divide the original equation by 5), and 3x − 8 is just 1 less:

$5\left(3x-7\right)=20\Rightarrow 3x-7=4\Rightarrow 3x-8=3$

Example 46

If 7x + 3y = 17 and 3x + 7y = 19, what is the average (arithmetic mean) of x and y?

The obvious way to do this is to first find x and y by solving the two equations simultaneously and then to take their average. If you are familiar with this method, try it now, before reading further. If you work carefully, you should find that $x=\frac{31}{20}$ and $y=\frac{41}{20}$, and their average is $\frac{\frac{31}{20}+\frac{41}{20}}{2}=\frac{9}{5}$ or 1.8. This method is not too difficult; but it is quite time-consuming.

Look for a shortcut. Is there a way to find the average without first finding x and y? Absolutely! Here’s the best way to do this.

Solution. Add the two equations:

$\begin{array}{r}\hfill 7x+3y=17\\ \hfill \underset{¯}{+3x+7y=19}\\ \hfill 10x+10y=36\end{array}$

Divide each side by 10:

$x+y=3.6$

Calculate the average:

$\frac{x+y}{2}=\frac{3.6}{2}=1.8$

When you learn TACTIC 16, you will see that adding two equations, as was done here, is the standard way to attack problems such as this on the SAT.

Pay Attention to Units.

Often the answer to a question must be in units different from those used in the given data. As you read the question, underline exactly what you are being asked. Do the examiners want hours or minutes or seconds, dollars or cents, feet or inches, meters or centimeters? On multiple-choice questions an answer with the wrong units is almost always one of the choices.

Example 47

At a speed of 48 miles per hour, how many minutes will be required to drive 32 miles?

(A) $\frac{2}{3}$

(B) $\frac{3}{2}$

(C) 40

(D) 2400

Solution. This is a relatively easy question. Just be attentive. Since $\frac{32}{48}=\frac{2}{3}$, it will take $\frac{2}{3}$ of an hour to drive 32 miles. Choice A is $\frac{2}{3}$; but that is not the correct answer because you are asked how many minutes will be required. (Did you underline the word “minutes” in the question?) The correct answer is $\frac{2}{3}\left(60\right)=40\left(C\right)$.

Note that you could have been asked how many seconds would be needed, in which case the answer would be 40(60) = 2400 (D).

Example 48

The wholesale price of potatoes is usually 3 pounds for $1.79. How much money, in cents, did a restaurant save when it was able to purchase 600 pounds of potatoes at 2 pounds for $1.15?

Solution. For 600 pounds the restaurant would normally have to buy 200 3-pound bags for 200 × $1.79 = $358. On sale, it bought 300 2-pound bags for 300 × $1.15 = $345. Therefore, the restaurant saved 13 dollars. Do not grid in 13. If you underline the word “cents” you won’t forget to convert the units: 13 dollars is 1300 cents.

Use Your Calculator.

You already know that you can use a calculator on the longer math section of the SAT. (See Chapter 5 for a complete discussion of calculator usage.) The main reason to use a calculator is that it enables you to do arithmetic more quickly and more accurately than you can by hand on problems that you know how to solve. (For instance, in Example 48, you should use your calculator to multiply 200 × 1.79.) The purpose of TACTIC 12 is to show you how to use your calculator to get the right answer to questions that you do not know how to solve or you cannot solve.

Example 49

If x² = 2, what is the value of $\left(x+\frac{1}{x}\right)\left(x-\frac{1}{x}\right)$?

(A) 1

(B) 1.5

(C) $1+\sqrt{2}$

(D) $2+\sqrt{2}$

Solution. The College Board would consider this a hard question, and most students would either take a wild guess or, worse, spend time working on it, and still miss it. The best approach is to realize that $\left(x+\frac{1}{x}\right)\left(x-\frac{1}{x}\right)$ is a product of the form

$\left(a+b\right)\left(a-b\right)=a^2-b^2$

Therefore:

$\left(x+\frac{1}{x}\right)\left(x-\frac{1}{x}\right)=x^2-\frac{1}{x^2}=2-\frac{1}{2}=1.5\left(B\right)$

If you didn’t see this solution, you could still solve the problem by writing $x=\sqrt{2}$ and then trying to multiply and simplify $\left(\sqrt{2}+\frac{1}{\sqrt{2}}\right)\left(\sqrt{2}-\frac{1}{\sqrt{2}}\right)$. It is likely, however, that you would make a mistake somewhere along the way.

The better method is to use your calculator: $\sqrt{2}\approx 1.414$ and $\frac{1}{\sqrt{2}}\approx 0.707$, so

$\left(\sqrt{2}+\frac{1}{\sqrt{2}}\right)\left(\sqrt{2}-\frac{1}{\sqrt{2}}\right)\approx \left(1.414+0.707\right)\left(1.414-0.707\right)=(2.121)\left(0.707\right)=1.499547$

Clearly, choose 1.5, the small difference being due to the rounding off of $\sqrt{2}$ as 1.414.

Example 50

If a and b are positive numbers, with a³ = 3 and a⁵ = 12b², what is the ratio of a to b?

Solution. This is another difficult question that most students would just guess the answer. If you think to divide the second equation by the first, however, the problem is not too bad:

$\begin{array}{ccc}\frac{a^5}{a^3}=\frac{12b^2}{3}=4b^2& \text{and}& \frac{a^5}{a^3}=a^2\end{array}$

Then

$a^2=4b^2\Rightarrow \frac{a^2}{b^2}=4\Rightarrow \frac{a}{b}=2$

If you don’t see this, you can still solve the problem with your calculator:

$\begin{array}{c}a=\sqrt[3]{3}\approx 1.44225\Rightarrow a^5={\left(1.44225\right)}^5\approx 6.24026\Rightarrow b^2=\frac{6.24026}{12}\approx 0.52\\ \Rightarrow b\approx \sqrt{0.52}\approx 0.7211\end{array}$

So, $\frac{a}{b}\approx \frac{1.44225}{0.7211}=2.00007$

Grid in 2.

Example 51

What is the value of $\frac{1+\frac{7}{5}}{1-\frac{5}{7}}$?

Solution. There are two straightforward ways to do this: (i) multiply the numerator and denominator by 35, the LCM of 5 and 7, and (ii) simplify and divide:

(i) $\frac{35\left(1+\frac{7}{5}\right)}{35\left(1-\frac{5}{7}\right)}=\frac{35+49}{35-25}=\frac{84}{10}=8.4$

(ii) $\frac{1+\frac{7}{5}}{1-\frac{5}{7}}=\frac{\frac{12}{5}}{\frac{2}{7}}=\frac{\stackrel{6}{\cancel{12}}}{5}\times \frac{7}{\underset{1}{\cancel{2}}}=\frac{42}{5}=8.4$

However, if you don’t like working with fractions, you can easily do the arithmetic on your calculator. Be sure you know how your calculator works. Be sure that when you evaluate the given complex fraction you get 8.4.

If this had been a multiple-choice question, the four choices would probably have been fractions, in which case the correct answer would be $\frac{42}{5}$. If you had solved this with your calculator, you would then have had to use the calculator to determine which of the fractions offered as choices was equal to 8.4.

Know When Not to Use Your Calculator.

Don’t get into the habit of using your calculator on every problem involving arithmetic. Since many problems can be solved more easily and faster without a calculator, learn to use your calculator only when you need it (see Chapter 5).

Example 52

John had $150. He used 85% of it to pay his electric bill and 5% of it on a gift for his mother. How much did he have left?

Solution. Many students would use their calculators on each step of this problem.

Electric bill: $150 × .85 = $127.50

Gift for mother: $150 × .05 = $7.50

Total spent: $127.50 + $7.50 = $135

Amount left: $150 − $135 = $15

Good test-takers would have proceeded as follows, finishing the problem in less time than it takes to calculate the first percent: John used 90% of his money, so he had 10% left; and 10% of $150 is $15.

Systematically Make Lists.

When a question asks “how many,” often the best strategy is to make a list of all the possibilities. It is important that you make the list in a systematic fashion so that you don’t inadvertently leave something out. Often, shortly after starting the list, you can see a pattern developing and can figure out how many more entries there will be without writing them all down.

Even if the question does not specifically ask “how many,” you may need to count some items to answer it; in this case, as well, the best plan may be to make a list.

Listing things systematically means writing them in numerical order (if the entries are numbers) or in alphabetical order (if the entries are letters). If the answer to “how many” is a small number (as in Example 53, below), just list all possibilities. If the answer is a large number (as in Example 54), start the list and write enough entries to enable you to see a pattern.

Example 53

The product of three positive integers is 300. If one of them is 5, what is the least possible value of the sum of the other two?

Solution. Since one of the integers is 5, the product of the other two is 60 (5 × 60 = 300). Systematically, list all possible pairs, (a, b), of positive integers whose product is 60, and check their sums. First, let a = 1, then 2, and so on.

a	b	a + b
1	60	61
2	30	32
3	20	23
4	15	19
5	12	17
6	10	16

The answer is 16.

Example 54

A palindrome is a number, such as 93539, that reads the same forward and backward. How many palindromes are there between 100 and 1000?

Solution. First, write down

the numbers in the 100’s 101, 111, 121, 131, 141,

that end in 1: 151, 161, 171, 181, 191

Now write the numbers 202, 212, 222, 232, 242,

beginning and ending in 2: 252, 262, 272, 282, 292

By now you should see the pattern: there are 10 numbers beginning with 1, and 10 beginning with 2, and there will be 10 beginning with 3, 4, ..., 9 for a total of 9 × 10 = 90 palindromes.

Example 55

In how many ways can Al, Bob, Charlie, Dan, and Ed stand in a line if Bob must be first and either Charlie or Dan must be last?

Solution. Represent the five boys as A, B, C, D, and E. Placing Charlie last, you see that the order is B __ __ __ C. Systematically fill in the blanks with A, D, and E. Write all the three-letter “words” you can in alphabetical order so you don’t accidentally skip one.

A D E

A E D

D A E

D E A

E A D

E D A

There are 6 possibilities when C is last. Clearly, there will be 6 more when D is last. Therefore, there are 12 ways in all to satisfy the conditions of the problem.

See Section P in Chapter 6 for additional examples and for another method of solving these problems using the counting principle.

Trust All Grids, Graphs, and Charts.

Figures that show the grid lines of a graph are always accurate, whether or not the coordinates of the points are given. For example, in the figure below, you can determine each of the following:

the lengths of all three sides of the triangle;

the perimeter of the triangle;

the area of the triangle;

the slope of each line segment.

Example 56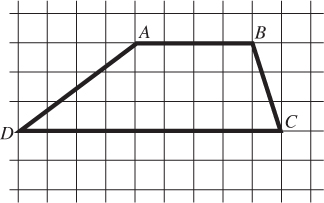

In the grid above, what is the area of quadrilateral ABCD?

(A) 19.5

(B) 21

(C) 25.5

(D) 27

Solution. $\overline{AB}$ and $\overline{CD}$ are parallel (they’re both horizontal), so ABCD is a trapezoid. If you know that the formula for the area of a trapezoid is $A=\frac{1}{2}\left(b_1+b_2\right)h$, use it. By counting boxes, you see that

$b_1=CD=9,b_2=AB=4,\text{and}h=3$

Therefore, the area is $\frac{1}{2}\left(9+4\right)\left(3\right)=19.5\left(A\right)$.

If you don’t know the formula, use $\overline{AE}$ and $\overline{BF}$ to divide ABCD into a rectangle (ABFE) and two right triangles (AED and BFC). Their areas are 12, 6, and 1.5, respectively, for a total area of 19.5.

For sample problems using grids, see Section 6-N on coordinate geometry.

SAT problems that use any kind of charts or graphs are always drawn accurately and can be trusted. For example, suppose that you are told that each of the 1000 students at Central High School studies exactly one foreign language. Then, from the circle graph that follows, you may conclude that fewer than half of the students study Spanish, but more students study Spanish than any other language; that approximately 250 students study French; that fewer students study German than any other language; and that approximately the same number of students are studying Latin and Italian.

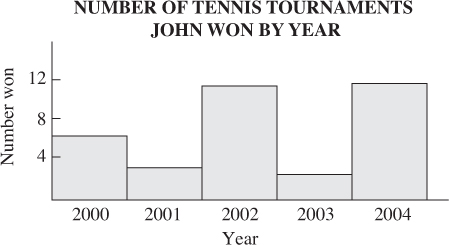
From the bar graph that follows, you know that in 2001 John won exactly three tournaments, and you can calculate that from 2000 to 2001 the number of tournaments he won decreased by 50% (from 6 to 3), whereas from 2001 to 2002 the number increased by 300% (from 3 to 12).

Example 57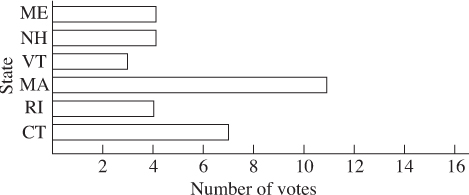

The chart above depicts the number of electoral votes assigned to each of the six New England states. What is the average (arithmetic mean) number of electoral votes, to the nearest tenth, assigned to these states?

(A) 5.0

(B) 5.5

(C) 6.0

(D) 6.5

Solution. Since you can trust the chart to be accurate, the total number of electoral votes for the six states is

$4+4+3+11+4+7=33$

and the average is 33 6 = 5.5 (B).

Several different types of questions concerning bar graphs, circle graphs, line graphs, and various charts and tables can be found in Section 6-O.

Add Equations.

When a question involves two equations that do not have exponents, either add the equations or subtract them. If there are three or more equations, add them.

Example 58

If 3x + 5y = 14 and x − y = 6, what is the average of x and y?

(A) 2.5

(B) 3

(C) 3.5

(D) 5

Solution. Add the equations:

$\begin{array}{r}\hfill \begin{array}{cc}3x+5y=14& \end{array}\\ \hfill \underset{¯}{\begin{array}{cc}+x-y=6& \end{array}}\\ \hfill \begin{array}{cc}4x+4y=20& \end{array}\end{array}$

Divide each side by 4:

$x+y=5$

The average of x and y is their sum divided by 2:

$\frac{x+y}{2}=\frac{5}{2}=2.5$

The answer is (A).

Note that you could have actually solved for x and y [x = 5.5, y = −0.5], and then taken their average. However, that would have been time-consuming and unnecessary.

Here are two more problems involving two or more equations.

Example 59

If a − b + c = 7 and a + b − c = 11, which of the following statements MUST be true?

  I. a is positive

 II. b > c

III. bc< 0

(A) I only

(B) II only

(C) III only

(D) I and II only

Example 60

If a − b = 1, b − c = 2, and c − a = d, what is the value of d?

(A) −3

(B) −1

(C) 1

(D) 3

Solution 59. Start by adding the two equations:

$\begin{array}{r}\hfill \begin{array}{cc}a-b+c=7& \end{array}\\ \hfill \underset{¯}{\begin{array}{cc}+a+b-c=11& \end{array}}\\ \hfill \begin{array}{cc}2a=18& \end{array}\end{array}$

Therefore, a = 9. (I is true.)

Replace a by 9 in each

$\begin{array}{ccc}9-b+c=7& \Rightarrow & -b+c=-2\Rightarrow b=c+2\end{array}$

equation to obtain and

two new equations:

$\begin{array}{ccc}9+b-c=11& \Rightarrow & b-c=2\Rightarrow b=c+2\end{array}$

Since b = c + 2, then b > c. (II is true.)

As long as b = c + 2, however, there are no restrictions on b and c: if b = 2 and c = 0, bc = 0; if

b = 4 and c = 2, then bc > 0. (III is false.)

The answer is (D).

Solution 60. Add the three equations:

$\begin{array}{l}\begin{array}{r}\hfill a-b=1\\ \hfill b-c=2\\ \hfill \underset{¯}{+c-a=d}\end{array}\\ \begin{array}{ccc}& 0=3+d\Rightarrow d=-3& \end{array}\end{array}$

The answer is (A).

PRACTICE EXERCISES

Multiple-Choice Questions

1. In 1995, Diana read 10 English books and 7 French books. In 1996, she read twice as many French books as English books. If 60% of the books that she read during the 2 years were French, how many English and French books did she read in 1996?

(A) 16

(B) 26

(C) 32

(D) 48

2. In the figure below, if the radius of circle O is 10, what is the length of diagonal $\overline{AC}$ of rectangle OABC?

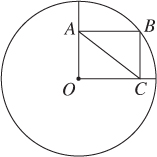
(A) $\sqrt{2}$

(B) $\sqrt{10}$

(C) $5\sqrt{2}$

(D) 10

3. In the figure below, vertex Q of square OPQR is on a circle with center O. If the area of the square is 8, what is the area of the circle?

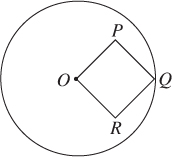
(A) 8π

(B) $8\pi \sqrt{2}$

(C) 16π

(D) 32π

4. In the figure below, ABCD is a square and AED is an equilateral triangle. If AB = 2, what is the area of the shaded region?

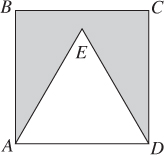
(A) $\sqrt{3}$

(B) 2

(C) $4-2\sqrt{3}$

(D) $4-\sqrt{3}$

5. If 5x + 13 = 31, what is the value of $\sqrt{5x+31}$?

(A) $\sqrt{13}$

(B) $\sqrt{\frac{173}{5}}$

(C) 7

(D) 13

6. At Nat’s Nuts a $2\frac{1}{4}$-pound bag of pistachio nuts costs $6.00. At this rate, what is the cost, in cents, of a bag weighing 9 ounces?
(Note: 1 pound = 16 ounces)

(A) 24

(B) 150

(C) 1350

(D) 2400

7. If 12a + 3b = 1 and 7b − 2a = 9, what is the average (arithmetic mean) of a and b?

(A) 0.1

(B) 0.5

(C) 1

(D) 2.5

8. Jessica has 4 times as many books as John and 5 times as many as Karen. If Karen has more than 40 books, what is the least number of books that Jessica can have?

(A) 220

(B) 210

(C) 205

(D) 200

9. What is the largest integer, n, that satisfies the inequality n² + 8n − 3 < n² + 7n + 8?

(A) 5

(B) 7

(C) 10

(D) 11

10. If a < b and c is the sum of a and b, which of the following is the positive difference between a and b?

(A) 2a − c

(B) 2 b − c

(C) c − 2b

(D) c − a + b

11. If w widgets cost c cents, how many widgets can you get for d dollars?

(A) $\frac{100dw}{c}$

(B) $\frac{dw}{100c}$

(C) $\frac{dw}{c}$

(D) cdw

12. If 120% of a is equal to 80% of b, which of the following is equal to a + b?

(A) 1.5a

(B) 2a

(C) 2.5a

(D) 3a

13. Which of the following numbers can be expressed as the product of three different integers greater than 1?

I. 25

II. 36

III. 45

(A) I only

(B) II only

(C) III only

(D) II and III only

14. What is the average of 4y + 3 and 2y − 1?

(A) 3y + 1

(B) 3y + 2

(C) 3y + 3

(D) 3y + 4

15. If x and y are integers such that x³ = y², which of the following CANNOT be the value of y?

(A) 1

(B) 8

(C) 16

(D) 27

16. What is a divided by a% of a?

(A) $\frac{a}{100}$

(B) $\frac{100}{a}$

(C) $\frac{a^2}{100}$

(D) $\frac{100}{a^2}$

17. If an object is moving at a speed of 36 kilometers per hour, how many meters does it travel in 1 second?

(A) 10

(B) 36

(C) 100

(D) 360

18. For what value of x is 8^{2x − 4} = 16^x?

(A) 2

(B) 4

(C) 6

(D) 8

19. On a certain Russian-American committee, $\frac{2}{3}$ of the members are men, and $\frac{3}{8}$ of the men are Americans. If $\frac{3}{5}$ of the committee members are Russians, what fraction of the members are American women?

(A) $\frac{3}{20}$

(B) $\frac{11}{60}$

(C) $\frac{1}{4}$

(D) $\frac{2}{5}$

20. If x% of y is 10, what is y?

(A) $\frac{10}{x}$

(B) $\frac{100}{x}$

(C) $\frac{1000}{x}$

(D) $\frac{x}{10}$

Grid-in Questions

21. In writing all of the integers from 1 to 300, how many times is the digit 1 used?

22. If a + 2b = 14 and 5a + 4b = 16, what is the average (arithmetic mean) of a and b?

23. In the figure below, the area of circle O is 12. What is the area of the shaded sector?

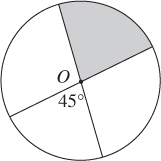
Note: Figure not drawn to scale

24. At a certain university, $\frac{1}{4}$ of the applicants failed to meet minimum standards and were rejected immediately. Of those who met the $\frac{2}{5}$ standards, were accepted.

If 1200 applicants were accepted, how many applied?

25. How many integers between 1 and 1000 are the product of two consecutive integers?

Answer Key

1. (D)

2. (D)

3. (C)

4. (D)

5. (C)

6. (B)

7. (B)

8. (A)

9. (C)

10. (B)

11. (A)

12. (C)

13. (B)

14. (A)

15. (C)

16. (B)

17. (A)

18. (C)

19. (A)

20. (C)

21.

22.

23.

24.

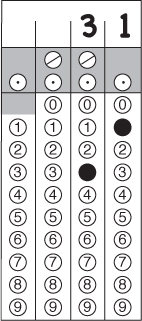
25.

Answer Explanations

Note: For many problems, an alternative solution, indicated by two asterisks (**), follows the first solution. In this case, one of the solutions is the direct mathematical one and the other is based on one of the tactics discussed in this chapter.

1. (D) Use TACTIC 1: draw a diagram representing a pile of books or a bookshelf.

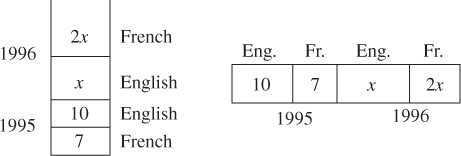
Better yet, draw a table:

	1995	1996	Total
English	10	x	10 + x
French	7	2x	7 + 2x
Total	17	3x	17 + 3x

In the 2 years, the number of French books Diana read was 7 + 2x, and the total number of books was 17 + 3x. Then 60% or $\frac{3}{5}=\frac{7+2x}{17+3x}$. To solve, cross-multiply:

$35+10x=51+9x\Rightarrow x=16$

In 1996, Diana read 16 English books and 32 French books, a total of 48 books.

2. (D) If you can’t solve this problem, use TACTIC 2: trust the diagram. $\overline{AC}$ is clearly longer than $\overline{OC}$, and very close to radius $\overline{OE}$ (measure them).

Therefore, AC must be about 10. Either by inspection or with your calculator, check the choices. They are approximately as follows:

(A) $\sqrt{2}=1.4$

(B) $\sqrt{10}=3.1$

(C) $5\sqrt{2}=7$

(D) 10

The answer must be 10.

**The answer is 10. The two diagonals are equal, and diagonal $\overline{OB}$ is a radius.

3. (C) As in question 2, if you get stuck trying to answer this, use TACTIC 2: look at the diagram.

Square OPQR, whose area is 8, takes up most of the quarter circle, so the area of the quarter circle is certainly between 11 and 14. The area of the whole circle is 4 times as great: between 44 and 56. Check the choices. They are approximately as follows:

(A) 8π = 25

(B) $8\pi \sqrt{2}=36$

(C) 16π = 50

(D) 32π = 100

The answer is clearly 16π.

**Use TACTIC 4: draw in line segment $\overline{OQ}$. Since the area of the square is 8, each side is $\sqrt{8}$, and diagonal $\overline{OQ}$ is $\sqrt{8}\cdot \sqrt{2}=\sqrt{16}=4$. But $\overline{OQ}$ is also a radius, so the area of the circle is π(4)² = 16π.

4. (D) Use TACTIC 9: subtract to find the shaded area. The area of square ABCD is 4. The area of ΔAED is $\frac{2^2\sqrt{3}}{4}=\frac{4\sqrt{3}}{4}=\sqrt{3}$ (see Section 6-J). Then the area of the shaded region is $4-\sqrt{3}$.

**Use TACTIC 2: trust the diagram. The area of the square is 4 and the white area clearly takes up less than half of the square. So the white area is less than 2, and the shaded area is more than 2, but definitely less than 3. Only choice (D) $(4-\sqrt{3})$ works.

5. (C) Use TACTIC 10: don’t do more than you have to. In particular, don’t solve for x. Here 5x + 13 = 31 ⇒ 5x = 18. So, $\sqrt{5x+31}=\sqrt{18+31}=\sqrt{49}=7$.

6. (B) This is a relatively simple ratio, but use TACTIC 11 and make sure you get the units right. You need to know that there are 100 cents in a dollar and 16 ounces in a pound.

$\frac{\text{price}}{\text{weight}}:\frac{6\text{dollars}}{2.25\text{pounds}}\frac{600\text{cents}}{36\text{ounces}}=\frac{x\text{cents}}{9\text{ounces}}$

Now cross-multiply and solve: 36x = 5400 ⇒ x = 150.

7. (B) Use TACTIC 16, and add the two equations to get

$\begin{array}{c}10a+10b=10\Rightarrow a+b=1\Rightarrow \\ \frac{a+b}{2}=\frac{1}{2}=0.5\end{array}$

Remember TACTIC 10: don’t do more than you have to. In particular, do not solve for a and b.

8. (A) Use TACTIC 5: backsolve. Since you want the least number, start with the smallest answer, (D). If Jessica had 200 books, Karen would have 40; but Karen has more than 40, so 200 is too small. Neither 205 (C) nor 210 (B) is a multiple of 4, so John wouldn’t have a whole number of books. Finally, 220 works.

**Since Karen has at least 41 books, Jessica has at least 205. But Jessica’s total must be a multiple of 4 and 5, hence of 20. The smallest multiple of 20 greater than 205 is 220.

9. (C) Use TACTIC 5: backsolve (using your calculator). Test the choices, starting with (D) (since you want the largest value):

${11}^2+8\left(11\right)-3=121+88-3=206$

and

${11}^2+7\left(11\right)+8=121+77+8=206$

The two sides are equal. When n = 10, however, the left-hand side is smaller:

$\begin{array}{ccc}100+80-3=177& \text{and}& 100+7\end{array}0+8=178$

**n² + 8n − 3 < n² + 7n + 8 ⇒ n < 11.

10. (B) Use TACTIC 6. Pick simple values for a, b, and c. Let a = 1, b = 2, and c = 3. Then b − a = 1. Only choice (B), 2b − c, is equal to 1 when b = 2 and c = 3.

**c = a + b ⇒ a = c − b.

So, b − a = b − (c − b) = 2b − c.

11. (A) Use TACTIC 6: replace variables with numbers. If 2 widgets cost 10 cents, then widgets cost 5 cents each; and for 3 dollars, you can get 60 widgets. Which of the choices equals 60 when w = 2, c = 10, and d = 3?

Only $\frac{100dw}{c}$.

**Convert d dollars to 100d cents, and set the ratios equal: $\frac{\text{widgets}}{\text{cents}}=\frac{w}{c}=\frac{x}{100d}$.

Multiply both sides by 100d: $x=\frac{100dw}{c}$.

12. (C) Use TACTIC 7: choose appropriate numbers. Since 120% of 80 = 80% of 120, let a = 80 and b = 120. Then a + b = 200. Which of the choices equals 200 when a = 80? Only 2.5a.

13. (B) Treat the number in each of the three Roman numeral choices as a separate true/false question.

Could 25 be expressed as the product of three different integers greater than 1? No, 25 has only two positive factors greater than 1 (5 and 25), and so clearly cannot be the product of three different positive factors. (I is false.)

Could 36 be expressed as the product of three different positive factors? Yes, 36 = 2 × 3 × 6. (II is true.)

Could 45 be expressed as the product of three different integers greater than 1? No, the factors of 45 that are greater than 1 are 3, 5, 9, 15, and 45; no three of them have a product equal to 45. (III is false.)

Only II is true.

14. (A) To find the average, add the two quantities and divide by 2:

$\frac{\left(4y+3\right)+\left(2y-1\right)}{2}=\frac{6y+2}{2}=3y+1$

**Use TACTIC 6. Let y = 1. Then 4y + 3 = 7 and 2y − 1 = 1. The average of 7 and 1 is $\frac{7+1}{2}=4$. Of the five choices, only 3y + 1 is equal to 4 when y = 1.

15. (C) Use TACTIC 5: test the choices. When there is no advantage to starting with any particular choice, start with (D). Could y = 27? Is there an integer x such that x³ = 27² = 729? Use your calculator to evaluate $\sqrt[3]{729}$ or test some numbers: 10³ = 1000—too large; 9³ = 729 works.

Try choice (C): 16. Is there an integer x such that x³ = 16² = 256? No: 5³ = 125, 6³ = 216, so 5 and 6 are too small; but 7³ = 343, which is too large. Alternatively, use your calculator to see that $\sqrt[3]{256}$ is not an integer.

The answer is 16.

16. (B) $a÷(a\%\text{of}a)=a÷\left(\frac{a}{100}\times a\right)=a÷\left(\frac{a^2}{100}\right)=a\times \frac{100}{a^2}=\frac{100}{a}$

**Use TACTICS 6 and 7: replace a by a number; use 100 since the problem involves percents.

$100÷\left(100\%\text{of}100\right)=100÷100=1$

Test each choice; which one equals 1 when a = 100?

A and B: $\frac{100}{100}=1$.

Eliminate (C) and (D); and test (A) and (B) with another value, 50, for a:

$50÷\left(50\%\text{of}50\right)=50÷\left(25\right)=2$

Now, only $\frac{100}{a}$ works: $\frac{100}{50}=2$.

17. (A) Set up a ratio:

$\frac{\text{distance}}{\text{time}}=\frac{36\text{kilometers}}{1\text{hour}}=\frac{36,000\text{meters}}{60\text{minutes}}=\frac{36,000\text{meters}}{3600\text{seconds}}=10\text{meters/second}$

**Use TACTIC 5: Test choices, starting with 100, choice (C):

$\begin{array}{l}100\text{meters/second}=6000\text{meters/minute}=\\ 360,000\text{meters/hour}=360\text{kilometers/hour}\end{array}$

Not only is that result too big, but it is too big by a factor of 10. The answer is 10, choice (A).

18. (C) Use TACTIC 5: backsolve, using your calculator. Let x = 4: then 8^{2(4) − 4} = 8⁴ = 4096, whereas 16⁴ = 65,536. Eliminate (A) and (B), and try a larger value.

Let x = 6: then

$8^{2\left(6\right)}=8^8=16,777,216$

and

${16}^6=16,777,216$

**8^{2x − 4} = 16^x ⇒ (2³)^{2x − 4} = (2⁴)^x.

Then 3(2x − 4) = 4x ⇒ 6x − 12 = 4x and so 2x = 12 ⇒ x = 6.

19. (A) Use TACTIC 7: choose appropriate numbers. The LCM of all the denominators is 120, so assume that the committee has 120 members.

Then there are $\frac{2}{3}\times 120=80$ men and 40 women. Of the 80 men, $30\left(\frac{3}{8}\times 80\right)$ are Americans. Since there are $72\left(\frac{3}{5}\times 120\right)$ Russians, there are 120 − 72 = 48 Americans of whom 30 are men, so the other 18 are women. This is illustrated in both the Venn diagram and the table below.

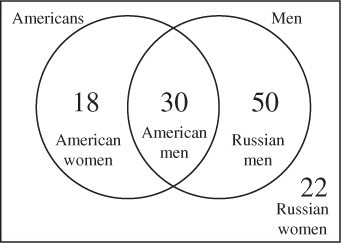
	Men	Women	Total
Americans	30	18	48
Russians	50	22	72
Total	80	40	120

Finally, the fraction of American women is $\frac{18}{120}=\frac{3}{20}$.

20. (C) Use TACTICS 6 and 7. Since 100% of 10 is 10, let x = 100 and y = 10. When x = 100, choices (C) and (D) are each 10. Eliminate (A) and (B), and try some other numbers: 50% of 20 is 10.

Of (C) and (D), only $\frac{1000}{x}=20$ when x = 50.

21. 160 Use TACTIC 14. Systematically list the numbers that contain the digit 1, writing as many as you need to see the pattern. Between 1 and 99 the digit 1 is used 10 times as the units digit (1, 11, 21, …, 91) and 10 times as the tens digit (10, 11, 12, …, 19) for a total of 20 times. From 200 to 299, there are 20 more times (the same 20 but preceded by 2). Finally, from 100 to 199 there are 20 more plus 100 numbers where the digit 1 is used in the hundreds place. The total is 20 + 20 + 20 + 100 = 160.

22. $\frac{5}{2}or2.5$ Use TACTIC 10: don’t do more than is necessary. You don’t need to solve this system of equations; you don’t need to know the values of a and b, only their average. Use TACTIC 17. Add the two equations:

$6a+6b=30\Rightarrow a+b=5$

Then, $\frac{a+b}{2}=\frac{5}{2}$ or 2.5.

23. $\frac{12}{8}or\frac{3}{2}or1.5$ The shaded sector is $\frac{45}{360}=\frac{1}{8}$ of the circle, so its area is of $\frac{1}{8}$ 12: $\frac{12}{8}$ or $\frac{3}{2}$ or 1.5. (Note that, since $\frac{12}{8}$ fits in the grid, it is not necessary to reduce it or to convert it to a decimal. See Chapter 5.)

**If you didn’t see that, use TACTIC 3 and redraw the figure to scale by making the angle as close as possible to 45°. It is now clear that the sector is $\frac{1}{8}$ of the circle (or very close to it).

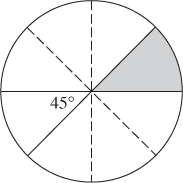
24. 4000 Use TACTIC 7: choose an appropriate number. The LCD of $\frac{1}{4}$ and $\frac{2}{5}$ is 20, so assume that there were 20 applicants. Then $\frac{1}{4}\left(20\right)=5$ failed to meet the minimum standards. Of the remaining 15 applicants, $\frac{2}{5}$, or 6, were accepted, so 6 of every 20 applicants were accepted. Set up a proportion:

$\frac{6}{20}=\frac{1200}{x}\Rightarrow 6x=24,000\Rightarrow x=4000$

25. 31 Use TACTIC 14. List the integers systematically: 1 × 2, 2 × 3, ..., 24 × 25, ... . You don’t have to multiply and list the products (2, 6, 12, ..., 600, ...); you just have to know when to stop. The largest product less than 1000 is 31 × 32 = 992, so there are 31 integers.