ExamplePART FIVE consists of this Introduction and two extremely important chapters. Chapter 5 presents several important strategies that can be used on many of the mathematics questions that appear on the SAT. Chapter 6 contains a complete review of the mathematics you need to know in order to do well on the SAT, as well as hundreds of sample problems.
Five different types of tactics are discussed in this book.
1. General Tactics. In the Introduction you learned many basic tactics used by all good test takers. These include: never waste time reading directions; read each question carefully; pace yourself; don’t get bogged down on any one question; eliminate as many choices as you can before guessing, but always guess; don’t leave any question unanswered. These tactics apply to all four sections of the SAT.
2. In Chapter 1, you learned the important tactics needed for handling the questions in the reading test.
3. In Chapter 3, you learned tactics for handling the different types of writing skills questions, and in Chapter 4 you learned strategies for writing a good essay.
4. In Chapter 5, you will find all of the tactics that apply to the mathematics sections of the SAT. Specific strategies are presented to deal with each type of multiple-choice and grid-in question found on the SAT test.
5. In Chapter 6, you will learn or review all of the mathematics that is needed for the SAT, and you will master the tactics and key facts that apply to each of the different mathematical topics.
Using these tactics will enable you to answer more quickly many problems that you already know how to do. The greatest value of these tactics, however, is that they will allow you to answer correctly, or make educated guesses on, problems that you do not know how to do .
How much time you initially devote to Chapter 6 should depend on how good your math skills are. If you are an excellent student who consistently earns A’s in math, you can initially skip the instructional parts of Chapter 6. If, however, while taking the practice tests in Part Six, you find that you keep making mistakes on certain types of problems (averages, percentages, geometry, etc.) or if you are spending too much time on them, you should then study the appropriate sections of Chapter 6. Even if your math skills are excellent, and you don’t need the review, you should do the sample questions in those sections; they are an excellent source of additional SAT questions. If you know that your math skills are not very good, it is advisable to review the material in Chapter 6, including working out the problems, before tackling the practice tests in Part Six.
No matter how good you are in math, you should carefully read and do the sample problems in Chapter 5. For many of these problems, two solutions are given: the most direct mathematical solution and a solution using one or more of the special tactics taught in these chapters.
Throughout the book, the symbol “⇒” is used to indicate that one step in the solution of a problem follows immediately from the preceding one, and that no explanation is necessary.
You should read:
as “2x = 12 implies that x = 6,” or, “ since 2x = 12, then x = 6.”
Here is a sample solution, using ⇒, to the following problem:
What is the value of 3x2 – 7 when x = –5?
When the reason for a step is not obvious, ⇒ is not used: rather, an explanation is given, often including a reference to a KEY FACT from Chapter 6. In many solutions, some steps are explained, while others are linked by the ⇒ symbol, as in the following example:
ExampleIn the diagram at the right, if w = 30, what is z?
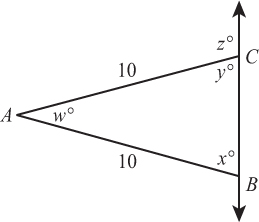
By KEY FACT J1, w + x + y = 180.
Since ΔABC is isosceles, x = y [KEY FACT J3].
Therefore, w + 2y = 180 ⇒ 30 + 2y = 180 ⇒ 2y = 150 ⇒ y = 75.
Finally, since y + z = 180 [KEY FACT I2], 75 + z = 180 ⇒ z = 105.
In Chapters 5 and 6, you will see seven headings that will appear either in the text or in the margins. They will indicate valuable information and will help to guide you as you study this book. Here is a brief explanation of each heading.
A useful strategy for attacking a certain type of problem.Some TACTICS give you advice on how to handle multiple-choice questions, regardless of the subject matter. Others point out ways to handle specific subject matter, such as finding averages or solving equations, regardless of the type of problem.
Key Fact
An important mathematical fact that you should commit to memory because it comes up often on the SAT.
REFERENCE FACT
A basic mathematical fact that is included in the “Reference Information” that appears on the first page of every math section.
HELPFUL HINT
A useful idea that will help you solve a problem more easily or avoid a pitfall.
CAUTION: A warning of a potential danger. Often a CAUTION points out a common error or a source of careless mistakes.
CALCULATOR SHORTCUT
A method of using your calculator, even when it is unnecessary, to help you get an answer faster than you otherwise might. Often this heading will signal an unusual or nonstandard way of using your calculator that you might not think of.
CALCULATOR HINT
Often, a way of using your calculator to get an answer that you could get more quickly without the calculator if you only knew how. CALCULATOR HINTS allow you to use your calculator to get answers to questions on which you would otherwise have to make a wild guess.
Before doing any of the work in Part Three and the practice tests in Part Four, you should reread the short discussion in Part One on the use of calculators on the SAT. As you do the sample problems in this book, always have available the calculator you intend to take to the SAT, and use it whenever you think it will be helpful. Throughout the rest of the book, whenever the use of a calculator is recommended, the icon has been placed next to the example or question. Remember:
In the 25-minute math section, you may NOT use a calculator.
In the 55-minute math section, many—but definitely not all—of the questions do require the use of a calculator.
Because students’ mathematical knowledge and arithmetic skills vary considerably, the decision as to when to use a calculator is highly subjective. Consider the following rather easy problem. Would you use a calculator?
What is the average (arithmetic mean) of 301, 303, and 305?
Let’s analyze the four possibilities:
1. Some students would use their calculators twice: first to add, 301 + 303 + 305 = 909, and then to divide, 909 3 = 303.
2. Others would use their calculators just once: to add the numbers; these students would then divide mentally.
3. Others would not use their calculators at all, because they could add the three numbers mentally faster than they could on a calculator. (Just say to yourself: 300, 300, and 300 is 900; and 1 + 3 + 5 is 9 more.)
4. Finally, others would do no calculations whatsoever. They would realize that the average of any three consecutive odd integers is the middle one: 301, 303, 305.
NOTE: The more the calculator was used, the longer it took to solve the problem. Use your calculator only when it will really save you time or if you think you will make a mistake without it.
HELPFUL HINT
In general in the 55-minute math section, you should do almost no arithmetic longhand. If you can’t do a calculation mentally, use your calculator. In particular, avoid long division and multiplication in which the factors have two or more digits. If you know that 132 = 169, terrific; if not, it’s better to use your calculator than to multiply with paper and pencil.
At the beginning of each math section, you will see the following directions and notes.
Directions: For each multiple-choice question, solve each problem and choose the best answer from the given choices. Fill in the corresponding circle on your answer document. For each grid-in question, solve the problem and fill in the answer on the answer sheet grid.
Notes:
Calculators ARE NOT PERMITTED in Section 3. Calculators ARE PERMITTED in Section 4.
All variables and expressions represent real numbers unless indicated otherwise.
All figures are drawn to scale unless indicated otherwise.
All figures are in a plane unless indicated otherwise.
Unless indicated otherwise, the domain of a given function is the set of all real numbers x for which the function has real values.
Immediately preceding Question 16 in Section 3 and Question 31 in Section 4, you will see the following set of instructions.
Grid-in Response Directions
First solve the problem, and then enter your answer on the grid provided on the answer sheet. The instructions for entering your answers follow.
First, write your answer in the boxes at the top of the grid.
Second, grid your answer in the columns below the boxes.
Use the fraction bar in the first row or the decimal point in the second row to enter fractions and decimals.
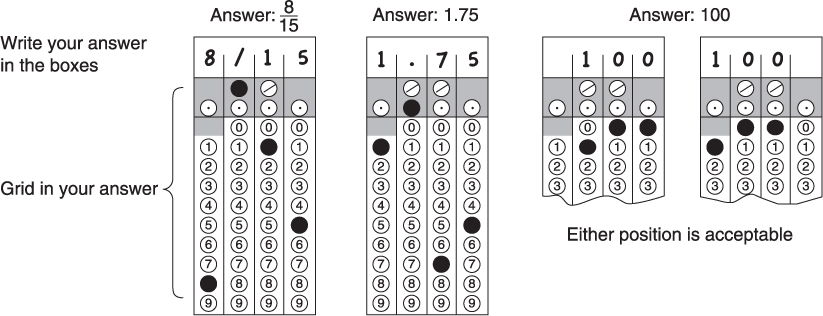
Grid only one space in each column.
Entering the answer in the boxes is recommended as an aid in gridding but is not required.
The machine scoring your exam can read only what you grid, so you must grid-in your answers correctly to get credit.
If a question has more than one correct answer, grid-in only one of them.
The grid does not have a minus sign; so no answer can be negative .
A mixed number must be converted to an improper fraction or a decimal before it is gridded. Enter as 5/4 or 1.25; the machine will interpret 11/4 as and mark it wrong.
All decimals must be entered as accurately as possible. Here are three acceptable ways of gridding
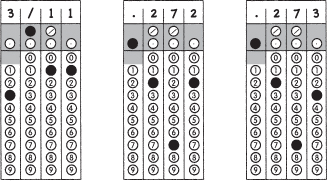
Note that rounding to .273 is acceptable because you are using the full grid, but you would receive no credit for .3 or .27, because they are less accurate.
On the first page of every mathematics section of the SAT, a box labeled “Reference Information” contains several basic math facts and formulas. In each math section of every practice test in this book, you will find the exact same information.
REFERENCE INFORMATION
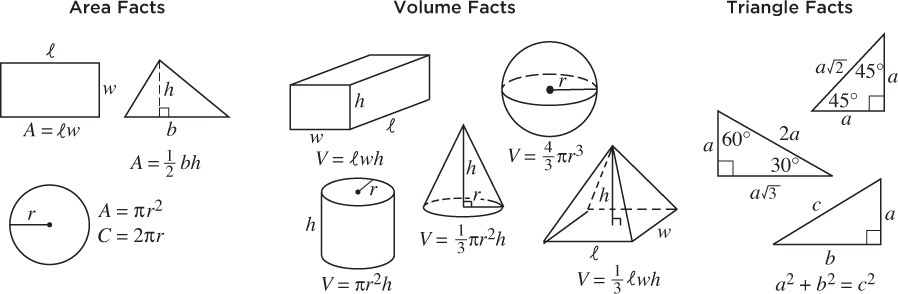
The arc of a circle contains 360°.
The arc of a circle contains 2π radians.
The sum of the measures of the angles in a triangle is 180°.
The College Board’s official guide, SAT Preparation Booklet, offers the following tip:
The test does not require you to memorize formulas. Commonly used formulas are provided in the test booklet at the beginning of each mathematical section.
HELPFUL HINT
As your prepare for this test, memorize the directions for each section. When you take the SAT, do not waste even one second reading directions.
If you interpret this to mean “Don’t bother memorizing the formulas provided,” this is terrible advice. It may be reassuring to know that, if you should forget a basic geometry fact, you can look it up in the box headed “Reference Information,” but you should decide right now that you will never have to do that. During the test, you don’t want to spend any precious time looking up facts that you can learn now. All of these “commonly used formulas” and other important facts are presented in Chapter 6. As you learn and review these facts, you should commit them to memory.
On multiple-choice questions, once you determine which answer choice you believe is correct, blacken the corresponding oval on the answer sheet. For grid-in questions the situation is a little more complicated.
For each math seciton, the answer sheet will have one blank grid for each grid-in question. Each one will look exactly like the grid on the next page. After solving a problem, the first step is to write the answer in the four boxes at the top of the grid. You then blacken the appropriate oval under each box. For example, if your answer to a question is 2.45, you write 2.45 at the top of the grid, one digit or symbol in each box, and then in each column blacken the oval that contains the number or symbol you wrote at the top of the column. (See the grid on the next page.) This is not difficult; but there are some special rules concerning grid-in questions, so let’s go over them before you practice gridding-in some numbers.
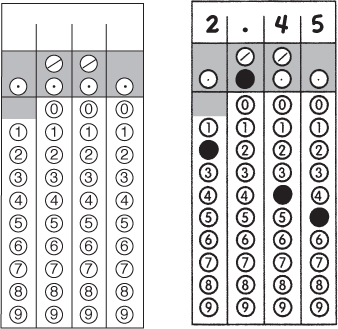
1. THE ANSWER TO EVERY GRID-IN QUESTION IS A POSITIVE NUMBER OR ZERO. The only symbols that appear in the grid are the digits 0 to 9, a decimal point, and a slash (/), used to write fractions. Note that there is no negative sign.
2. BE AWARE THAT YOU WILL RECEIVE CREDIT FOR A CORRECT ANSWER NO MATTER WHERE YOU GRID IT. For example, the answer 17 could be gridded in any of three positions:
Nevertheless, try to consistently write all your answers the way numbers are usually displayed—to the right, with blank spaces at the left.
3. DO NOT ROUND OFF ANY ANSWER UNLESS YOU ARE SPECIFICALLY TOLD TO DO SO.
For example, suppose the answer to a question is .148. If the question asks what is the value to the nearest hundredth, you must enter .15. You will receive no credit if you entered .148. On the other hand, if the question did not ask you to round off your answer, you will receive no credit for entering .15 since you could enter .148, which is more accurate.
If a decimal answer will not fit in the grid, enter a decimal point in the first column, followed by the first three digits. For example, if your answer is 0.454545..., enter it as .454. You would receive credit if you rounded it to .455, but don’t. You might occasionally make a mistake in rounding, whereas you’ll never make a mistake if you just copy the first three digits. Note: If the correct answer has more than two decimal digits, you must use all four columns of the grid. You will receive no credit for .4 or .5 or .45. (These answers are not accurate enough.)
4. NEVER WRITE A 0 BEFORE THE DECIMAL POINT. The first column of the grid doesn’t even have a 0 in it. If the correct answer is 0.3333..., you must grid it as .333. You can’t grid 0.33, and 0.3 is not accurate enough.
5. NEVER REDUCE FRACTIONS.
If your answer is a fraction that will fit in the grid, such as or or , just enter it. Don’t waste time reducing it or converting it to a decimal.
If your answer is a fraction that won’t fit in the grid, do not attempt to reduce it; use your calculator to convert it to a decimal. For example, won’t fit in a grid—it would require five spaces: 2 4 / 6 5. Don’t waste even a few seconds trying to reduce it; just divide on your calculator, and enter .369.
Unlike , the fraction can be reduced—to , which doesn’t help, or to or , either of which could be entered. Don’t do it! Reducing a fraction takes time, and you might make a mistake. You won’t make a mistake if you just use your calculator: 24 64 = .375.
6. BE AWARE THAT YOU CAN NEVER ENTER A MIXED NUMBER. If your answer is , you cannot leave a space and enter your answer as 2 1/2. Also, if you enter 
, the machine will read it as and mark it wrong. You must enter as the improper fraction or as the decimal 2.5.
7. FULL CREDIT IS GIVEN FOR ANY EQUIVALENT ANSWER. USE THESE GUIDELINES TO ENTER YOUR ANSWER IN THE SIMPLEST WAY. If your answer is , you should enter 6/9. (However, credit would be given for any of the following: 2/3, 4/6, 8/12, .666, .667.)
8. IF A GRID-IN QUESTION HAS MORE THAN ONE CORRECT ANSWER, GRID IN ONLY ONE OF THE ACCEPTABLE ANSWERS. For example, if a question asked for a positive number less than 100 that was divisible by both 5 and 7, you could enter either 35 or 70, but not both. Similarly, if a question asked for a number between and , you could enter any one of more than 100 possibilities: fractions such as and or any decimal between .429 and .554—.43 or .499 or .52, for example.
9. BE SURE TO ENTER AN ANSWER FOR EVERY GRID-IN QUESTION. Remember that since there is no penalty for an incorrect answer, never leave out any question on the SAT. If you are running out of time, just grid in any number, such as 1, in each grid when you have 10 seconds left.
10. BE SURE TO GRID EVERY ANSWER VERY CAREFULLY. The computer does not read what you have written in the boxes; it reads only the answer in the grid. If the correct answer to a question is 100 and you write 100 in the boxes, but accidentally grid in 200, you get no credit.
11. WRITE EACH ANSWER IN THE BOXES. If you know that the answer to a question is 100, can you just grid it in and not bother writing it on top? Yes, you will get full credit, and so some SAT guides recommend that you don’t waste time writing the answer. This is terrible advice. Write each answer in the boxes. It takes less than 2 seconds per answer to do this, and it definitely cuts down on careless errors in gridding. Equally important, if you go back to check your work, it is much easier to read what’s in the boxes on top than what’s in the grid.
12. NOTE THE LIMITATIONS OF THE GRID. Be aware that the smallest number that can be gridded is 0; the largest is 9999. No number greater than 100 can have a decimal point. The largest number less than 100 that can be gridded is 99.9; the smallest number greater than 100 that can be gridded is 101.
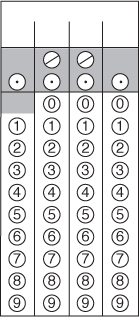
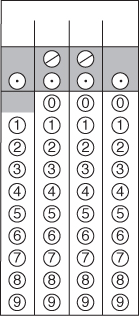
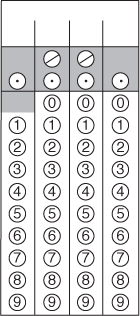
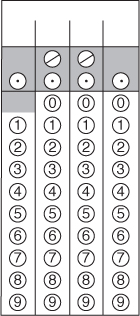
Now, check your understanding of these guidelines. Use the empty numbered grids that follow to show how you would enter these answers.
1. 123
2.
3.
4.
5. 1.1111...
6. 0
7.
8.
9.
10.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
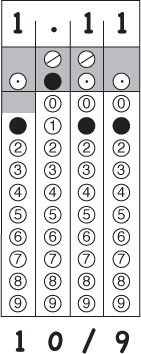
Each grid shows the recommended answer. Other acceptable answers, if any, are written below each grid.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
If you missed even one of these, go back and reread the rules for gridding. You never want to solve a problem correctly but get no credit because you didn’t grid it properly. Whenever you practice grid-in problems, actually grid in the answers. Make sure you understand all of these rules now. When you actually take the SAT, don’t even look at the instructions for gridding.