© Springer Nature Switzerland AG 2019
M. H. Soffel, W.-B. HanApplied General RelativityAstronomy and Astrophysics Libraryhttps://doi.org/10.1007/978-3-030-19673-8_11

11. Light-Rays

Michael H. Soffel1  and Wen-Biao Han2
(1)
Institute of planetary geodesy, Lohrmann-Observatory, Dresden, Germany
(2)
Shanghai Astronomical Observatory, Chinese Academy of Sciences, Shanghai, China
 

11.1 Historical Remarks

The theoretical basis for modelling astrometric measurements is the analysis of the light-ray equation, or the equation of null geodesics. Only for a few gravitational systems such as black-hole space-times, exact solutions for null geodesics are known (e.g., Chandrasekhar 1983; Hackmann 2014; Hackmann et al. 2008a,b, 2010). For more complex situations, e.g., for the propagation of light-rays in the gravitational field of solar system bodies, one might resort to approximation schemes such as the post-Newtonian (PN) or the post-Minkowskian approximation. At the first PN (1PN) level one approximates the exact null-geodesic trajectory x γ(t) in some suitably chosen coordinate system (ct, x) by neglecting c −3 terms, in the 2PN approximation one neglects c −5 terms. In the first post-Minkowskian approximation (1PM) one neglects G 2 terms, in the 2PM approximation G 3 terms etc.1

1PN Light Propagation in the Field of Monopoles at Rest

The largest effect in light deflection in the solar system is due to the masses (monopoles) of the massive solar system bodies. The standard post-Newtonian solution of light trajectory in the gravitational field of a mass monopole at rest has been discussed in Chap. 8. An upper limit for the light deflection angle (the angle between vectors m and k in Fig. 11.1) in the field of a body at rest to 1PN order is given by
$$\displaystyle \begin{aligned} \varphi^{\mathrm{M}}_{\mathrm{1PN}} \le \frac{4 G M_A}{c^2 d_A}\, , {} \end{aligned} $$
(11.1.1)
where d A is the (constant) distance of closest approach of the unperturbed light-ray to the mass M A.

1PN Light Propagation in the Field of Quadrupoles at Rest

The effects of light deflection in a quadrupole gravitational field at rest have been investigated many times by several authors. However, for the first time the full analytical solution for the light trajectory in a quadrupole field in post-Newtonian approximation has been obtained by Klioner (1991b), where an explicit time dependence of the coordinates of a photon and the solution of the boundary value problem for the geodesic equations has been obtained. These results were confirmed by a different approach by Le Poncin-Lafitte et al. (2008), while simplified expressions for 1 μas astrometric accuracy and rigorous estimates about the magnitude of quadrupole effects on light deflection have been derived by Zschocke and Klioner (2011).

1PN Light Propagation in the Field of Higher Multipole Moments at Rest

Light deflection effects from higher mass multipole moments at rest have been studied by Le Poncin-Lafitte et al. (2008). For a single body M A one finds
$$\displaystyle \begin{aligned} \varphi^{J_n}_{\mathrm{1PN}} \le \frac{4 G M_A}{c^2}\frac{\left|J_n^A\right|\,\left(R_A\right)^n}{\left(d_A\right)^{n+1}}\, , {} \end{aligned} $$
(11.1.2)
where $$J_n^A$$ and R A are the dimensionless parameter of zonal harmonics and a (coordinate) radius of the gravitating body A.

1.5PN Light Propagation in the Field Spin-Dipoles at Rest

The first explicit 1.5PN (considering also c −3 terms in the photon trajectory) solution of the light trajectory in the gravitational field of massive bodies at rest possessing a spin-dipole has been obtained by Klioner (1991a,b). This solution provides all the details of light propagation, especially the explicit time dependence of the coordinates of the photon and the solution of the corresponding boundary value problem. An upper limit for the 1.5PN spin-dipole light deflection is given by
../images/447007_1_En_11_Chapter/447007_1_En_11_Equ3_HTML.png
(11.1.3)
where S A indicates the spin of the gravitating body.

1.5PN Light Propagation in the Field of Arbitrary Time-Independent Multipoles at Rest

A systematic approach to the integration of light geodesic equations in the stationary 1.5PN gravitational field of an isolated body with time-independent multipole moments, M L and S L, is contained in Kopeikin (1997).

1PN and 1.5PN Light Propagation in the Field of Moving Monopoles

Since the massive bodies of the Solar system are moving the center of mass coordinates of some body A are functions of time. For to-days astrometric accuracies at the microarcsecond level one has to account for the problem of how to treat the motion of the massive bodies during the time of propagation of light from the point of emission to the point of reception. An analytical integration of 1PN light trajectory in the field of a uniformly moving body has first been derived by Klioner (1989). One has
$$\displaystyle \begin{aligned} \varphi^{\mathrm{M}}_{\mathrm{1PN}} \le \frac{4 G M_A}{c^2 d_A(s)} \, , {} \end{aligned} $$
(11.1.4)
where s indicates retarded time, i.e.,
$$\displaystyle \begin{aligned} \begin{array}{rcl} s = t_1 - \frac{\left|{\mathbf{x}}_1 - {\mathbf{x}}_A\left(s\right)\right|}{c}\,, {} \end{array} \end{aligned} $$
(11.1.5)
the observer is located at x 1 at coordinate time t 1 and the spatial position of the body at retarded time is x A(s). So to a first approximation one gets the old result for a mass monopole at rest, with d A being replaced by d A(s). If velocity terms are taken into account (Kopeikin et al. 1999; Kopeikin and Makarov 2007; Zschocke 2015) one obtains
$$\displaystyle \begin{aligned} \varphi^{\mathrm{M}}_{\mathrm{1.5PN}} \le \frac{4 G M_A}{c^2 d_A(s)}\,\frac{v_A(s)}{c}\,. {} \end{aligned} $$
(11.1.6)

1PM Light Propagation in the Field of Moving Monopoles

A rigorous solution of the problem of light propagation in the field of arbitrarily moving monopoles and in the first post-Minkowskian approximation has been found by Kopeikin and Schäfer (1999). By applying advanced integration methods introduced in Kopeikin (1997) and further developed by Kopeikin et al. (1999), the authors succeeded in integrating the geodesic equations for photons using retarded potentials, so that the positions of gravitating bodies are computed at the retarded instant of time s according to the light cone equation. Using this rigorous approach Kopeikin and Schäfer (1999) have shown that if the positions and velocities of the bodies are taken at retarded time then the effects of acceleration and the effects due to the time dependence of velocity of the bodies are much smaller than 1 μas in the solar system.

1PN Light Propagation in the Field of Moving Quadrupoles

The light deflection at moving massive bodies with mass and quadrupoles has been investigated by Kopeikin and Makarov (2007), where the quadrupole term is taken in the Newtonian limit. Using the elaborated integration methods mentioned above, they succeeded to integrate analytically the geodesic equations by neglecting all terms smaller than 1 μas.

1PM Light Propagation in the Field of Moving Spin-Dipoles

Kopeikin and Mashhoon (2002) have derived analytical solutions in post-Minkowskian approximation for the case of light propagation in the field of arbitrarily moving bodies possessing a mass monopole and a spin-dipole.

1PM Light Propagation in the Field of Time-Dependent Multipoles

The case of the propagation of light rays in the field of localized sources which are completely characterized by time-dependent mass and spin multipole moments has been investigated by Kopeikin and Korobkov (2005) and Kopeikin et al. (2006). In particular, they have found an analytical solution for the light propagation in such gravitating systems.

1.5PN Light Propagation in the Field of Moving Multipoles

Zschocke (2016a) has recently solved the problem of light propagation in the 1.5PN approximation in the gravitational field of N arbitrarily moving bodies endowed with a full set of intrinsic mass-multipoles and spin-multipoles, employing the Kopeikin integration technique. Maximal orders of magnitude for moving zonal harmonics are
$$\displaystyle \begin{aligned} \varphi^{J_n}_{\mathrm{1.5PN}} \le \frac{4 G M_A}{c^2}\frac{\left|J_n^A\right|\,\left(R_A\right)^n}{\left(d_A(s)\right)^{n+1}} \, \left(1 + \frac{v_A(s)}{c} \right)\,. {} \end{aligned} $$
(11.1.7)

2PN Light Propagation in the Field of a Mass-Monopole at Rest

Post-post-Newtonian (2PN) effects on light deflection by some static mass have been investigated exhaustively in the literature (E.g., Epstein and Shapiro 1980; Fischbach and Freeman 1980; Richter and Matzner 1982a,b, 1983; Cowling 1984; Brumberg 1987; Bodenner and Will 2003; Le Poncin-Lafitte et al. 2004; Teyssandier and Le Poncin-Lafitte 2008; Ashby and Bertotti 2010). Accuracies have been determined by comparisons with numerical integrations of the null geodesic equation by Klioner and Zschocke (2010).

2PN Light Propagation in the Field of Arbitrarily Moving Point-Like Body

Recently, Zschocke (2016b) has solved the problem of light propagation in the field of a single arbitrarily moving point-like body in the 2PN approximation (see also Zschocke 2018b, 2019). For the 2PN problem with several (point-like) gravitating bodies only very limiting results have been published whose applicability is restricted (e.g., Bruegmann 2005).

Relevant physical parameters of solar system bodies are listed in Table 11.1.
Table 11.1

Numerical values for mass M A, radius R A, actual coefficients of zonal harmonics $$J_n^A$$ , distance between observer and body $$r_{A}^1$$ , orbital velocity v A of Sun, Jupiter and Saturn (JPL 2019)

Parameter

Sun

Jupiter

Saturn

GM A∕c 2 [m]

1476

1.4

0.4

P A [m]

696 × 106

71.5 × 106

60.3 × 106

$$J_2^A$$

2 × 10−7

14.696 × 10−3

16.291 × 10−3

$$J_4^A$$

−

− 0.587 × 10−3

− 0.936 × 10−3

$$J_6^A$$

−

0.034 × 10−3

0.086 × 10−3

$$J_8^A$$

−

− 2.5 × 10−6

− 10.0 × 10−6

$$J_{10}^A$$

−

0.21 × 10−6

2.0 × 10−6

S A [kg m2∕ s]

1.64 × 1041

4.15 × 1038

7.13 × 1037

v A∕c

4 × 10−8

4.4 × 10−5

3.2 × 10−5

The value for $$J^A_2$$ for the Sun is taken from Fienga et al. (2008), while $$J_n^A$$ with n = 2,  4,  6 for Jupiter and Saturn are taken from de Pater and Lissauer (2015), while $$J_n^A$$ with n = 8,  10 for Jupiter and Saturn are taken from Hubbard and Militzer (2016) and Anderson and Schubert (2007), respectively. The spin angular momenta S A are determined from the moment of inertia I A with the ratio $$ {I_A}/{M_A R_A^2} = 0.059, 0.254, 0.210$$ for Sun, Jupiter, Saturn, respectively (from NASA planetary fact sheets)

Orders of magnitude for gravitational light deflection effects in the solar system are presented in Table 11.2.
Table 11.2

Numerical magnitudes for light deflection angles in μas in the gravitational field of solar system bodies (Sun, Jupiter or Saturn) according to the upper limits given above

 

Sun

Jupiter

Saturn

$$\varphi _{\mathrm {1PN}}^{\mathrm {M}}$$

1.75 × 106

16.3 × 103

5.8 × 103

$$\varphi _{\mathrm {1PN}}^{J_2}$$

1

240

95

$$\varphi _{\mathrm {1PN}}^{J_4}$$

−

9.6

5.46

$$\varphi _{\mathrm {1PN}}^{J_6}$$

−

0.56

0.50

$$\varphi _{\mathrm {1PN}}^{J_8}$$

−

0.04

0.06

$$\varphi _{\mathrm {1PN}}^{J_{10}}$$

−

0.003

0.01

$$\varphi _{\mathrm {1.5PN}}^{\mathrm {M}}$$

0.1

0.8

0.2

$$\varphi _{\mathrm {1.5PN}}^{J_2}$$

−

0.011

0.003

$$\varphi _{\mathrm {1.5PN}}^{\mathrm {S}}$$

0.7

0.2

0.04

$$\varphi _{\mathrm {1.5PN}}^{\mathrm {SO}}$$

−

0.015

0.006

The physical parameters for Sun, Jupiter and Saturn are summarized in Table 11.1. The given light deflection angles are for grazing light-rays, i.e., for d A = R A. For the light deflection in the field of spin-octupole, $$\varphi _{\mathrm {1.5PN}}^{\mathrm {SO}}$$ , results of Meichsner (2015) where used. Blank entries indicate numbers smaller than 1 nas

In the following we will exhaustively discuss the 1PN problem of light-rays in the field of a single body at rest that has arbitrary mass and spin moments and then the Kopeikin-Schäfer formalism for 1PM accuracies and a system of N moving gravitating point-like masses.

11.2 Light-Rays for 1PN Stationary Multipoles

The geodesic equation (8.​5.​2) can be written in the form
$$\displaystyle \begin{aligned} {d^2 x^i \over dt^2} = - c^2 \Gamma^{i}_{ {0}{0}}{} - 2c \Gamma^{i}_{ {0}{j}}{} {\dot x}^j - \Gamma^{i}_{ {j}{k}}{} {\dot x}^j {\dot x}^k + \left[c \Gamma^{0}_{ {0}{0}}{} + 2 \Gamma^{0}_{ {0}{j}}{} {\dot x}^j + \frac 1c \Gamma^{0}_{ {j}{k}}{} {\dot x}^j {\dot x}^k \right] {\dot x}^i \end{aligned} $$
(11.2.1)
with x = x γ and
$$\displaystyle \begin{aligned} \dot x^i \equiv {dx_\gamma^i \over dt} \, . \end{aligned}$$
Inserting the post-Newtonian Christoffel symbols with the potential w and w i we get
$$\displaystyle \begin{aligned} {d^2 x^i \over dt^2} = w_{,i} \left( 1 + {\dot {\mathbf{x}}^2 \over c^2} \right) - {4 \over c^2} \left( {d {\mathbf{x}} \over dt} \cdot \nabla w \right){\dot x}^i + {4 \over c^2} \left( w^i_{,j} - w^j_{,i} \right) {\dot x}^j + {4 \over c^4} w^j_{,k} {\dot x}^i {\dot x}^j {\dot x}^k \, . \end{aligned} $$
(11.2.2)
Kopeikin (1997) succeeded to solve the post-Newtonian light-ray equation (11.2.2) for a central body endowed with arbitrary stationary mass- and spin-multipole moments for very remote light sources (note, the sign errors associated with the gravito-magnetic potential w i). Assuming the gravitating body to be located at the center of our coordinate system the two metric potentials, w and w i are given in the skeletonized harmonic gauge, according to (7.​4.​3) and (7.​4.​4):
$$\displaystyle \begin{aligned} w({\mathbf{x}}) = G \sum_{l \ge 0} {(-1)^l \over l!} M_L \partial_L \left( {1 \over r} \right) \end{aligned} $$
(11.2.3)
and
$$\displaystyle \begin{aligned} w^i({\mathbf{x}}) = - G \sum_{l \ge 1} {(-1)^l \over l!} {l \over l+1} \epsilon_{iab} S^{bL-1} \partial_{aL-1} \left( {1 \over r} \right) \, . \end{aligned} $$
(11.2.4)
Since we assume the Newtonian trajectory of be of the form x N(t) = x 0 + c n(t − t 0) we can replace dx i∕dt in each post-Newtonian term by cn i, so that the propagation equation reads:
$$\displaystyle \begin{aligned} {d^2 x^i \over dt^2} = 2 w_{,i} - 4 w_{,k} n^k n^i + {4 \over c} \left( w^i_{,j} - w^j_{,i} \right) n^j + {4 \over c} w^j_{,k} n^i n^j n^k \, . \end{aligned} $$
(11.2.5)
Inserting the expressions for w and w i we end up with
$$\displaystyle \begin{aligned} \begin{aligned} {d^2 x^i \over dt^2} =\ & (2 n^i n^j - P_{ij}) G \sum_{l \ge 0} {(-1)^l \over l!} M_L \partial_{<L>} \left( {x^j \over r^3} \right) \\ &+ {4 G \over c} \sum_{l \ge 1} {(-1)^l l \over (l+1)!} (\epsilon_{iab} n^j - \epsilon_{abc} n^c P_{ij}) S^{bL-1} \, \partial_{<aL-1>} \left( {x^j \over r^3} \right) \, , \end{aligned} \end{aligned} $$
(11.2.6)
where P ij are the components of the operator P ⊥ that projects perpendicular to n:
$$\displaystyle \begin{aligned} P_{ij} = \delta_{ij} - n^i n^j = P^i_j = P^{ij}\, . \end{aligned} $$
(11.2.7)
This projection operator has only two algebraically independent components and satisfies the relation
$$\displaystyle \begin{aligned} P^i_k P^k_j = (\delta_{ik} - n^i n_k)(\delta_{kj} - n^k n_j) = P^i_j \, . \end{aligned} $$
(11.2.8)
Let the 3-vector d be defined by projection of x perpendicular to n
$$\displaystyle \begin{aligned} {\mathbf{d}} = {\mathbf{P}}^\perp {\mathbf{x}} = {\mathbf{x}} - {\mathbf{n}} ({\mathbf{n}} \cdot {\mathbf{x}}) = {\mathbf{x}}_0 - {\mathbf{n}} ({\mathbf{n}} \cdot {\mathbf{x}}_0) = {\mathbf{n}} \times ({\mathbf{x}} \times {\mathbf{n}}) = {\mathbf{n}} \times ({\mathbf{x}}_0 \times {\mathbf{n}}) \end{aligned} $$
(11.2.9)
that satisfies
$$\displaystyle \begin{aligned} {\mathbf{d}} \cdot {\mathbf{n}} = 0 \, . \end{aligned} $$
(11.2.10)
This can also be expressed by the relation
$$\displaystyle \begin{aligned} P^i_j d^j = P^i_j P^j_k x^k = P^i_k x^k = d^i \, . \end{aligned} $$
(11.2.11)
The vector d points from the origin of Σx to the point of closest approach of the unperturbed light-ray to that origin.
The fact that d has only two independent components has a strange looking consequence:
$$\displaystyle \begin{aligned} {\partial d^i \over \partial d^k} = \partial_k d^i = \partial_k (P^i_j x^j) = P^i_k \, . \end{aligned} $$
(11.2.12)
Often, however, it might be convenient to consider the spatial components of d as formally independent so that
$$\displaystyle \begin{aligned} {\partial d^i \over \partial d^j} = \delta_{ij} \end{aligned} $$
(11.2.13)
with a subsequent projection perpendicular to n, i.e., the rule (11.2.13) can be used if everywhere we replace the operator
$$\displaystyle \begin{aligned} \partial^\perp_i \equiv {\partial \over \partial d^i} \qquad {\mathrm{by}} \qquad \hat \partial_i \equiv P^j_i \partial^\perp_i \, . \end{aligned} $$
(11.2.14)
We now use the Kopeikin-parametrization of the unperturbed light-ray equation (Kopeikin 1997) in the form
$$\displaystyle \begin{aligned} {\mathbf{x}} = {\mathbf{d}} + {\mathbf{n}} \cdot s \, , \end{aligned} $$
(11.2.15)
where
$$\displaystyle \begin{aligned} s = {\mathbf{n}} \cdot {\mathbf{x}} = c(t - t_0) + {\mathbf{n}} \cdot {\mathbf{x}}_0 \end{aligned} $$
(11.2.16)
is a time coordinate if we replace x by x N(t). Then the parameter s 0 = n ⋅x 0 corresponds to the time
$$\displaystyle \begin{aligned} t^* = t_0 - {\mathbf{n}} \cdot {\mathbf{x}}_0/c \, , \end{aligned} $$
(11.2.17)
which is the time of closest approach of the unperturbed light-ray to the origin of Σx. Thus,
$$\displaystyle \begin{aligned} s = c(t - t^*) \, ; \qquad s_0 = c(t_0 - t^*) \end{aligned} $$
(11.2.18)
or
$$\displaystyle \begin{aligned} s = c\tau \qquad {\mathrm{with}} \qquad \tau = t - t^* \, . \end{aligned} $$
(11.2.19)
Following Kopeikin (1997) we can now split the partial derivative with respect to x i in the form
$$\displaystyle \begin{aligned} \partial_i = \partial^\perp_i + \partial^\parallel_i \end{aligned} $$
(11.2.20)
with
$$\displaystyle \begin{aligned} \partial^\perp_i \equiv {\partial \over \partial d_i} \, , \qquad \partial^\parallel_i \equiv n^i {\partial \over \partial s} \, . \end{aligned} $$
(11.2.21)
I.e., one splits the partial derivative, ∂∕∂x i, into two pieces, one in the direction of the unperturbed light-ray and a second one perpendicular to it. From (r = |x|; ξ = |d|)
$$\displaystyle \begin{aligned} r^2 = \xi^2 + s^2 \end{aligned}$$
we get the useful relations
$$\displaystyle \begin{aligned} r - s = {d^2 \over r + s} \, ; \qquad r_0 - s_0 = {d^2 \over r_0 + s} \, . \end{aligned} $$
(11.2.22)

Exercise 11.1

  1. a)
    Let F(x) = 1∕r 3 = (x 2 + y 2 + z 2)−3∕2. First calculate ∂ i F(x); then substitute d + n s for x and compute
    $$\displaystyle \begin{aligned} (\partial_i^\perp + n^i \partial_s) F({\mathbf{d}} + {\mathbf{n}} s) \, . \end{aligned}$$

    Compare the two results with each other.

     
  2. b)

    Do the same for an arbitrary function F(x) = F(|x|) = F(r).

     

Solution

  1. a)
    F ,i = −3x i∕r 5 . Since r 2 = d j d j + s 2 we have F(d + n s) = (d j d j + s 2)−3∕2. Then,
    $$\displaystyle \begin{aligned} \begin{array}{rcl} \partial^\perp_i F({\mathbf{d}} + {\mathbf{n}} s) &\displaystyle =&\displaystyle - {3 d^i \over r^5} \\ \partial_s F({\mathbf{d}} + {\mathbf{n}} s) &\displaystyle =&\displaystyle - {3 s \over r^5} \end{array} \end{aligned} $$

    so that $$(\partial ^\perp _i + n^i \partial _s) F({\mathbf {d}} + {\mathbf {n}} s)$$ gives the same as ∂ i F(x).

     
  2. b)

    F ,i = F ,r(x i∕r). F(d + n s) = F[(d i d i + s 2)1∕2] so that $$\partial ^\perp _i F = F_{,r} (d^i/r)$$ and ∂ s F = F ,r(s∕r) and $$(\partial ^\perp _i + n^i \partial _s) F({\mathbf {d}} + {\mathbf {n}} s) = F_{,i}$$ .

     

Lemma 11.1

$$\displaystyle \begin{aligned} \partial_{<L>} = \sum_{p=0}^l {l! \over p! (l-p)!} n_{<P} \partial^\perp_{L-P>} \partial^p_s \, . \end{aligned} $$
(11.2.23)

The proof follows simply from (11.2.20) and the binomial formula.

An integration over the time variable ct is then equivalent to an integration over s or τ, where s ≡ cτ. Remember, that s = τ = 0 labels the instance of time where the unperturbed light-ray is at the point of closest approach to the gravitating body. The integration of the propagation equations is then easily performed with the following Lemma:

Lemma 11.2

$$\displaystyle \begin{aligned} \int^s_{- \infty} \partial_{<L>} \left( {x^j \over r^3} \right) \, ds = A^j_{<L>}(s) \end{aligned} $$
(11.2.24)
and
$$\displaystyle \begin{aligned} \int_{s_0}^s \int_{- \infty}^s \partial_{<L>} \left( {x^j \over r^3} \right) \, d\tau = B^j_{<L>}(s) - B^j_{<L>}(s_0) \end{aligned} $$
(11.2.25)
with
$$\displaystyle \begin{aligned} \begin{aligned} A^j_{<L>}(s) =\ & \partial^\perp_{<L>} \left[ {d^j \over d^2} \left( {s \over r} + 1 \right) - {n^j \over r} \right] \\ &+ \sum_{p = 1}^l {l! \over p! (l-p)!} n_{<P} \partial^\perp_{L-P>} \, \partial^{p-1}_s \left( {x^j \over r^3} \right) \end{aligned} \end{aligned} $$
(11.2.26)
and (L = aL − 1)
$$\displaystyle \begin{aligned} \begin{aligned} B^j_{<L>}(s) =\ & \partial^\perp_{<L>} \left[ {d^j \over d^2} (r + s) - n^j \ln (r + s) \right] \\ & + l \cdot n_{<a} \partial^\perp_{L-1>} \left( {d^j \over d^2} {s \over r} - {n^j \over r} \right) \\ & + \sum_{p=2}^l {l! \over p! (l-p)!} n_{<P} \partial^\perp_{L-P>} \partial^{p-2}_s \left( {x^j \over r^3} \right) \, . \end{aligned} \end{aligned} $$
(11.2.27)

Proof

$$\displaystyle \begin{aligned} \begin{aligned} & \int_{- \infty}^s \partial_{<L>} \left( {x^j \over r^3} \right) \, ds = \\ &\int_{-\infty}^s ds \left[\sum_{p=0}^l {l! \over p! (l-p)!} n_{<P} \partial^\perp_{L-P>} \partial^p_s \left( {x^j \over r^3} \right)\right] \, . \end{aligned} \end{aligned}$$
For p ≥ 1 we have at least one derivative with respect to s so that the integration over s can be carried out immediately. Therefore,
$$\displaystyle \begin{aligned} \begin{aligned} \int_{- \infty}^s \partial_{<L>} \left( {x^j \over r^3} \right) \, ds =& \int_{-\infty}^s \partial^\perp_{<L>} \left( {x^j \over r^3} \right)\, ds \\ &+ \sum_{p=1}^l {l! \over p! (l-p)!} n_{<P} \partial^\perp_{L-P>} \partial^{p-1}_s \left( {x^j \over r^3} \right)\, . \end{aligned} \end{aligned} $$
Inserting the Newtonian expressions, x i = n i s + d i and r = (d 2 + s 2)1∕2 one finds
$$\displaystyle \begin{aligned} \int^s_{- \infty} \left( {x^j \over r^3} \right) \, ds = - {n^j \over r} + {d^j \over d^2} \left( {s \over r} + 1 \right) \end{aligned}$$
which leads to the first part of the Lemma. The second part is demonstrated in a similar way.
With Lemma 11.2 we can integrate the light-ray equation considering all stationary mass-multipole moments
$$\displaystyle \begin{aligned} \begin{aligned} \dot x^i =\ & - 2 {G\over c} \sum_{l \ge 2} {(-1)^l \over l!} M_L \partial^\perp_{<L>} \left[ {d^i \over d^2} \left( {s \over r} + 1 \right) + {n^i \over r} \right] \\ &+ 2 {G\over c} \sum_{p \ge 2} \sum_{p=1}^l {(-1)^l \over p! (l-p)!} M_L n_{<P} \partial^\perp_{L-P>} \partial^{p-1}_s \left( {n^i s - d^i \over r^3} \right) \end{aligned} \end{aligned} $$
(11.2.28)
and
$$\displaystyle \begin{aligned} x^i = Q^i(s) - Q^i(s_0) \end{aligned} $$
(11.2.29)
with
$$\displaystyle \begin{aligned} \begin{aligned} & Q^i(s) = 2 (n^i n^j - P_{ij}) G \sum_{l \ge 2} {(-1)^l \over l!} M_L B^j_{<L>} \\ =\ & - {2 G \over c^2} \sum_{l \ge 2} {(-1)^l \over l!} M_L \partial^\perp_{<L>} \left[ {d^i \over d^2} (r + s) + n^i \ln (r + s) \right] \\ & - 2 {G \over c^2} \sum_{l \ge 2} {(-1)^l \over (l-1)!} M_{L} n_{<a} \partial^\perp_{L-1>} \left[ {d^i \over d^2} {s \over r} + {n^i \over r} \right] \\ & + 2 {G \over c^2} \sum_{l \ge 2} \sum_{p=2}^l {(-1)^l \over p! (l-p)!} M_L n_{<a_1} \dots n_{P} \partial^\perp_{L-P>} \partial^{p-2}_s \left( {n^i s - d^i \over r^3} \right) \, . \end{aligned} \end{aligned} $$
(11.2.30)
Similarly, for the influence of the spin-multipole moments upon light propagation one finds
$$\displaystyle \begin{aligned} \dot x_{\mathrm{S}}^i = 4 {G \over c} \sum_{l \ge 1} {(-1)^l \over l!} {l \over l+1} (\epsilon_{iab} n^j - \epsilon_{abc} n_c P_{ij}) S^{bL-1} A^j_{<aL-1>}(s) \end{aligned} $$
(11.2.31)
and
$$\displaystyle \begin{aligned} \begin{aligned} x^i_{\mathrm{S}} =\ & 4 {G \over c} \sum_{l \ge 1} {(-1)^l \over l!} {l \over l+1} (\epsilon_{iab} n^j - \epsilon_{abc} n^c P_{ij}) S^{bL-1} \left[ B^j_{<aL-1>} (s) - B^j_{<aL-1>} (s_0) \right] \, . \end{aligned} \end{aligned} $$
(11.2.32)

11.2.1 The Shapiro Time Delay

With
$$\displaystyle \begin{aligned} x^i - x^i_0 = n^i c(t - t_0) + x^i_{\mathrm{PN}} \end{aligned}$$
we obtain
$$\displaystyle \begin{aligned} c(t - t_0) = \vert {\mathbf{x}} - {\mathbf{x}}_0 \vert - n^i x^i_{\mathrm{PN}} = \vert {\mathbf{x}} - {\mathbf{x}}_0 \vert + \Delta_{\mathrm{M}} + \Delta_{\mathrm{S}} \, , \end{aligned} $$
(11.2.33)
where ΔM stands for the influence of the mass-multipole terms and ΔS for that of the spin-moments (the symbol |0 stands for the expression taken at the initial point)
$$\displaystyle \begin{aligned} \begin{aligned} \Delta_{\mathrm{M}} =\ & {2G \over c^2} \sum_{l=0}^\infty \sum_{p=0}^l {(-1)^l \over l!} {l! \over p! (l-p)!} M_L n_{<P} \partial^\perp_{L-P>} \partial_s^p \ln {s + r \over s_0 + r_0} - {\huge\vert}_0 \\ = \ & 2 {G \over c^2} \sum_{l \ge 0}{(-1)^l \over l!} M_L \partial^\perp_{<L>} \ln {r + s \over r_0 + s_0} \\ &+ 2 {G \over c^2} \sum_{l \ge 0} {(-1)^l \over (l-1)!} M_L n_{<a} \partial^\perp_{L-1>} \left( {1 \over r} - {1 \over r_0} \right) \\ & - 2 {G \over c^2} \sum_{l \ge 0} \sum_{p = 2}^l {(-1)^l \over p! (l-p)!} M_L n_{<P} \partial^\perp_{L-P>} \partial^{p-2}_s \left( {s \over r^3} \right) - {\huge\vert}_0 \end{aligned} \end{aligned} $$
(11.2.34)
and
$$\displaystyle \begin{aligned} \Delta_{\mathrm{S}} = {4G \over c^3} \sum_{l = 1}^\infty \sum_{p=0}^l {(-1)^l \over l!} {l! \over p! (l-p)!}{l \over l+1} \epsilon_{ijk} S_{kL-1} n_P \partial^\perp_{jL-P-1} \ln {s + r \over s_0 + r_0} - {\huge\vert_0} \, . \end{aligned} $$
(11.2.35)
These expression should be understood in the sense that every term containing some ill-defined expression should vanish.
For practical calculations the following is useful. Let
$$\displaystyle \begin{aligned} \Phi(s,{\mathbf{d}}) \equiv \ln(r + s) = \ln( \sqrt{d^2 + s^2} + s) \,, \end{aligned} $$
(11.2.36)
then the first derivatives appearing in (11.2.34) and (11.2.35) read:
$$\displaystyle \begin{aligned} \begin{array}{rcl} \partial_s \Phi &\displaystyle =&\displaystyle \frac 1r \end{array} \end{aligned} $$
(11.2.37)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \partial^2_s \Phi &\displaystyle =&\displaystyle - {s \over r^3} \end{array} \end{aligned} $$
(11.2.38)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \partial^\perp_a \Phi &\displaystyle =&\displaystyle {d^a \over r(r+s)} \end{array} \end{aligned} $$
(11.2.39)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \partial^\perp_a\partial_s \Phi &\displaystyle =&\displaystyle - {d^a \over r^3} \end{array} \end{aligned} $$
(11.2.40)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \partial^{\perp}_{<ab>} \Phi &\displaystyle =&\displaystyle - {(s + 2r) \over (r+s)^2 r^3} d^a d^b - {n^a n^b \over r(r+s)} \, , \end{array} \end{aligned} $$
(11.2.41)
where the last term results from (11.2.12).

11.2.1.1 The Monopole Time Delay

For a mass-monopole M we get
$$\displaystyle \begin{aligned} \Delta_{M, l=0}(t,t_0) = {2 GM \over c^2} \ln {r + s \over r_0 + s_0} = {2 GM \over c^2} \ln {r + {\mathbf{n}} \cdot {\mathbf{x}} \over r_0 + {\mathbf{n}} \cdot {\mathbf{x}}_0} \, . \end{aligned} $$
(11.2.42)

11.2.1.2 The Quadrupole Time Delay

Let us compute the time-delay term for a body with mass quadrupole moments:
$$\displaystyle \begin{aligned} \begin{aligned} \Delta_{\mathrm{M,l=2}} =\ & {G \over c^2} M_{ab} \partial^\perp_{<ab>} \ln {r + s \over r_0 + s_0} \\ &+ {2 G \over c^2} M_{ab} n_{<a} \partial^\perp_{b>} \left( {1 \over r} - {1 \over r_0} \right) \\ & - {G \over c^2} M_{ab} n_a n_b \left[ {s \over r^3} - {s_0 \over r_0^3} \right] \\ & = Q(s) - Q(s_0) \, . \end{aligned} \end{aligned} $$
(11.2.43)
with r = (d a d a + s 2)1∕2 we get
$$\displaystyle \begin{aligned} \partial^\perp_{ab} \ln (r + s) = - {1 \over r^2 (r + s)^2} d^a d^b - {1 \over r^3 (r + s)} d^a d^b + {1 \over r(r+s)} (\delta_{ab} - n^a n^b) \end{aligned}$$
and, finally,
$$\displaystyle \begin{aligned} Q(\tau) = -{2 G \over c^2} M_{ab} {n^a d^b \over r^3} - {G \over c^2} M_{ab} {n^a n^b \over d^2} \left(1 - {s^3 \over r^3} \right) - {G \over c^2} M_{ab} {d^a d^b \over d^4} \left( 2 - 3 {s\over r} + {s^3 \over r^3} \right) \, . \end{aligned} $$
(11.2.44)
A little bit of re-writing shows that
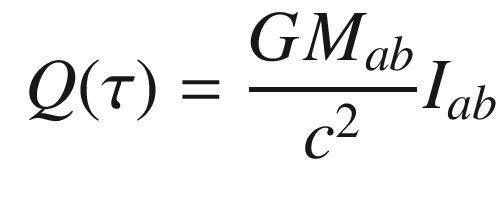
$$\displaystyle \begin{aligned} Q(\tau) = {G M_{ab} \over c^2} I_{ab} \end{aligned} $$
(11.2.45)
with
$$\displaystyle \begin{aligned} I_{ab} = - {2 n^a d^b \over r^3} - n^a n^b \left( {s \over r^3} + {1 \over r(r+s)} \right) - {d^a d^b (s + 2r) \over (r+s)^2 r^3 } \, . \end{aligned} $$
(11.2.46)
This expression agrees with the one given by Klioner (1991b):
$$\displaystyle \begin{aligned} I_{ab} = - {2 n^a d^b \over r^3} + n^a n^b \left( {{\mathbf{n}} \cdot {\mathbf{r}} \over r} \right) (d^{-2} - r^{-2}) + {d^a d^b \over d^2} \left[ {{\mathbf{n}} \cdot {\mathbf{r}} \over r} (2 d^{-2} + r^{-2}) \right] \, . \end{aligned} $$
(11.2.47)

11.2.1.3 The Spin Time Delay

Similarly for the influence of the spin dipole term we get
$$\displaystyle \begin{aligned} \Delta_{\mathrm{S}} = - {2 G \over c^3} \epsilon_{iab} n^i S^b\ \partial^\perp_a \ln {r + s \over r_0 + s_0} = 2 {G \over c^3}({\mathbf{n}} \times {\mathbf{S}}) \cdot ({\mathbf{F}}(s) - {\mathbf{F}}(s_0)) \end{aligned} $$
(11.2.48)
with
$$\displaystyle \begin{aligned} {\mathbf{F}} (s) = {{\mathbf{d}} \over r(r+s)} \, . \end{aligned} $$
(11.2.49)
Note, that d in the expression for F can be replaced by x.

11.2.2 The Time Transfer Function

The gravitational time delay can be computed in an easier way directly from the null condition, ds 2 = 0, along the light-ray. Writing g μν = η μν + h μν we get
$$\displaystyle \begin{aligned} dt^2 = {1 \over c^2} d{\mathbf{x}}^2 + \left( h_{00} + \frac 2c \, h_{0i} {dx^i \over dt} + {1 \over c^2} h_{ij} {dx^i \over dt} {dx^j \over dt} \right) \, dt^2 \end{aligned}$$
or
$$\displaystyle \begin{aligned} dt = {\vert d {\mathbf{x}} \vert \over c} + {\vert d {\mathbf{x}} \vert \over 2c} (h_{\mu\nu} n^\mu n^\nu) \,, \end{aligned} $$
(11.2.50)
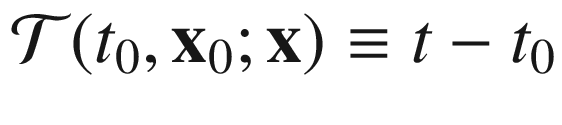where we have inserted $$\dot x^i = c n^i$$ from the unperturbed light-ray equation, x(t) = x 0 + n c(t − t 0) and n μ ≡ (1, n). For our post-Newtonian metric with potentials w and w i given by (11.2.3) and (11.2.4), the Time Transfer Function (TTF), $$\mathcal {T}(t_0,{\mathbf {x}}_0;{\mathbf {x}}) \equiv t - t_0$$ with ds = |x| reads
$$\displaystyle \begin{aligned} \mathcal{T}(t_0,{\mathbf{x}}_0; {\mathbf{x}}) = \frac Rc + {1 \over 2c} \int_{s_0}^s (h_{\mu\nu} n^\mu n^\nu) ds = \frac Rc + {2 \over c^3} \int_{s_0}^{s} \left( w - \frac 2c {\mathbf{w}} \cdot {\mathbf{n}} \right) \, ds \,. \end{aligned} $$
(11.2.51)
The TTF allows the computation of t if t 0, x 0 and x are given. The TTF-formalism is especially useful if combined with the Kopeikin-parametrization of the unperturbed light-ray (Kopeikin 1997). With expression (11.2.3) for w and (11.2.4) for w i we recover immediately our old results (11.2.34) and (11.2.35).

11.2.3 The TTF for a Body Slowly Moving with Constant Velocity

Let us now consider the situation where the gravitating body (called A) moves with a constant slow velocity v A; we will neglect terms of order $$v_{\mathrm {A}}^2$$ in this section following. Let us denote a canonical coordinate system moving with body A, X α = (cT, X a) and the corresponding metric potentials by W and W a. Under our conditions the transformation from co-moving coordinates X α to x μ is a linear Lorentz-transformation of the form (β A ≡v A∕c):
$$\displaystyle \begin{aligned} x^\mu = z_{\mathrm{A}}^\mu(T) + \Lambda^\mu_\alpha X^\alpha \end{aligned} $$
(11.2.52)
with $$z_{\mathrm {A}}^\mu \equiv (0,{\mathbf {z}}_{\mathrm {A}}(T))$$ and $$\Lambda ^0_0 = 1, \Lambda ^0_a = \beta _{\mathrm {A}}^a, \Lambda ^i_0 = \beta ^i_{\mathrm {A}}, \Lambda ^i_a = \delta _{ia}$$ . A transformation of the co-moving metric to the rest-system then yields
$$\displaystyle \begin{aligned} \begin{array}{rcl} {} w &\displaystyle =&\displaystyle W + {4 \over c} {\boldsymbol{\beta}}_{\mathrm{A}} \cdot {\mathbf{W}} \\ w_i &\displaystyle =&\displaystyle W v_{\mathrm{A}}^i + W_i \, . \end{array} \end{aligned} $$
(11.2.53)
In the following we will only consider a moving mass-monopole for which, in our approximation, w = GM∕r and w i = (GM∕r) ⋅ v i so that the TTF takes the form
$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathcal{T}(t_0,{\mathbf{x}}_0;{\mathbf{x}}) &\displaystyle =&\displaystyle \frac Rc + {2GM \over c^3} \int \left[ {(1 - 2 {\boldsymbol{\beta}}_{\mathrm{A}} \cdot {\mathbf{n}}) \over r} \right]\, ds \\ &\displaystyle =&\displaystyle \frac Rc + {2GM g_\beta \over c^3} \int { ds' \over r} \,, \end{array} \end{aligned} $$
(11.2.54)
where g β ≡ 1 −β A ⋅n and s′ = g β s.
We now parametrize the unperturbed light-ray in the form
$$\displaystyle \begin{aligned} {\mathbf{x}}_\tau = {\mathbf{z}}_{\mathrm{A}} + {\mathbf{d}}_\beta + {\mathbf{n}}_\beta \eta \,, \end{aligned} $$
(11.2.55)
where n β ≡g β∕g β, g β ≡n −β A, and d β = n β × (r A ×n β) is perpendicular to n β so that $$r_{\mathrm {A}}(t) = \sqrt { d_\beta ^2 + c^2\eta ^2}$$ and η = r A ⋅n β. The TTF therefore for our mass-monopole in uniform motion takes the form
$$\displaystyle \begin{aligned} \mathcal{T}_{{\mathrm{M}}, l=0} = 2 {G M_{\mathrm{A}} \over c^3} g_\beta \ln {r_{\mathrm{A}} + \eta \over r_{\mathrm{A}}^0 + \eta^0} \end{aligned}$$
and since η = n β ⋅r A = g β ⋅r A∕g β, we obtain
$$\displaystyle \begin{aligned} \mathcal{T}_{{\mathrm{M}}, l=0} = {2 G M_{\mathrm{A}}\over c^3}g_\beta \ln \left( {{\mathbf{g}}_\beta \cdot {\mathbf{r}}_{\mathrm{A}} + g_\beta r_{\mathrm{A}} \over {\mathbf{g}}_\beta \cdot {\mathbf{r}}_{\mathrm{A}}^0 + g_\beta r_{\mathrm{A}}^0} \right) \end{aligned} $$
(11.2.56)
in accordance with the results from the literature (e.g., Bertone et al. 2013).

11.3 Light-Rays to Post-Minkowskian Order

To understand the influence of the motion of gravitating bodies upon the trajectory of light-rays one might resort to a post-Minkowski approximation. This means that velocities of field generating bodies are treated to all orders in 1∕c, but terms proportional to the square of masses or the gravitational constant G will be neglected. Such a formalism has been worked out by Kopeikin and Schäfer (1999) for a system of N mass-monopoles M A, (A = 1, …, N) in a single global coordinate system Σx: x μ = (ct, x). In Σx they write the energy-momentum tensor in the form
$$\displaystyle \begin{aligned} \begin{array}{rcl}{} T^{\mu\nu} (t,{\mathbf{x}}) &\displaystyle =&\displaystyle \sum_{\mathrm{A}} \hat T^{\mu\nu}_{\mathrm{A}} (t) \delta({\mathbf{x}} - {\mathbf{x}}_{\mathrm{A}}(t)) \, , \end{array} \end{aligned} $$
(11.3.1)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \hat T^{\mu\nu}_{\mathrm{A}} (t) &\displaystyle =&\displaystyle M_{\mathrm{A}} \gamma_{\mathrm{A}}^{-1} (t) u_{\mathrm{A}}^\mu(t) u_{\mathrm{A}}^\nu(t) \, , {} \end{array} \end{aligned} $$
(11.3.2)
where x A(t) are the spatial coordinates of M A in Σx, v A(t) ≡ d x A(t)∕dt,
$$\displaystyle \begin{aligned} \gamma_{\mathrm{A}}(t) \equiv \left( 1 - {{\mathbf{v}}_{\mathrm{A}}^2(t) \over c^2} \right)^{-1/2} \end{aligned} $$
(11.3.3)
and
$$\displaystyle \begin{aligned} u_{\mathrm{A}}^\mu(t) = (\gamma_{\mathrm{A}}(t)c, \gamma_{\mathrm{A}}(t) {\mathbf{v}}_{\mathrm{A}}(t)) \end{aligned} $$
(11.3.4)
is the 4-velocity of M A. δ(x) is the usual 3-dimensional Dirac delta-distribution. Thus,
$$\displaystyle \begin{aligned} \hat T_{\mathrm{A}}^{00} = {M_{\mathrm{A}} c^2 \over \sqrt{1 - {\mathbf{v}}_{\mathrm{A}}/c^2}} \, ; \quad \hat T_{\mathrm{A}}^{0i} = {M_{\mathrm{A}} v_{\mathrm{A}}^i c \over \sqrt{1 - {\mathbf{v}}_{\mathrm{A}}/c^2}} \, ; \quad \hat T_{\mathrm{A}}^{ij} = {M_{\mathrm{A}} v_{\mathrm{A}}^i v_{\mathrm{A}}^j \over \sqrt{1 - {\mathbf{v}}_{\mathrm{A}}/c^2}} \, , \end{aligned} $$
(11.3.5)
where the components of the coordinate velocity $$v_{\mathrm {A}}^i$$ are functions of coordinate time t. Let us write
$$\displaystyle \begin{aligned} g^{\mu\nu} = \eta^{\mu\nu} + \tilde h^{\mu\nu} \end{aligned}$$
and assume the quantities $$\tilde h^{\mu \nu }$$ to be of first order in G. To PM-order quadratic and higher order terms in $$\tilde h^{\mu \nu }$$ will be neglected.
By (5.​8.​18) the solution for the field equations in harmonic gauge can be written in the form (remember that h μν refers to the gothic metric)
../images/447007_1_En_11_Chapter/447007_1_En_11_Equ69_HTML.png
(11.3.6)
The right hand side can be written as a type of PM Liénard-Wiechert potentials of the form
$$\displaystyle \begin{aligned} \tilde h^{\mu\nu} (t,{\mathbf{x}}) = {4 \over c^2} \sum_{\mathrm{A}} {\hat T_{\mathrm{A}}^{\mu\nu} - \frac 12 \eta^{\mu\nu} \hat T^\lambda_\lambda \over r_{\mathrm{A}} - {\boldsymbol{\beta}}_{\mathrm{A}} \cdot {\mathbf{r}}_{\mathrm{A}} } \, , \end{aligned} $$
(11.3.7)
where all A-quantities on the right hand side of this equation are functions of retarded time s A that is a solution of the light-cone equation
$$\displaystyle \begin{aligned} s_{\mathrm{A}} + \vert {\mathbf{x}} - {\mathbf{x}}_{\mathrm{A}}(s_{\mathrm{A}}) \vert/c = t \, . \end{aligned} $$
(11.3.8)
Here, r A(s A) ≡x −x A(s A), r A(s A) ≡|r A(s A)| and β A(s A) ≡v A(s A)∕c.
The geodesic equation to first order in G takes the form (x(t) = x γ(t)):
$$\displaystyle \begin{aligned} \begin{aligned} c^{-2} \ddot x^i(t) =\ & {1 \over 2} g_{00,i} - g_{0i,0} - {1 \over 2} g_{00,0} {\dot x^i \over c} - (g_{0i,j} - g_{0j,i}) {\dot x^j \over c} - g_{ij,0} {\dot x^j \over c}\\ & - g_{00,j} {\dot x^i \over c} {\dot x^j \over c} - \left( g_{ik,j} - {1 \over 2} g_{kj,i} \right) {\dot x^j \over c} {\dot x^k \over c} + \left( {1 \over 2} g_{jk,0} - g_{0k,j} \right) {\dot x^i \over c} {\dot x^j \over c} {\dot x^k \over c} \, . \end{aligned} \end{aligned} $$
(11.3.9)

Exercise 11.2

Proof equation (11.3.9) for linearized gravity.

Proof

The geodesic equation reads
$$\displaystyle \begin{aligned} c^{-2} \ddot x^i = - \Gamma^i_{00} - 2 \Gamma^i_{0j} {\dot x^j \over c} - \Gamma^i_{jk} {\dot x^j \over c} {\dot x^k \over c} + \Gamma^0_{00} {\dot x^i \over c} + 2 \Gamma^0_{0j} {\dot x^i \over c} {\dot x^j \over c} + \Gamma^0_{jk} {\dot x^i \over c} {\dot x^j \over c} {\dot x^k \over c} \end{aligned}$$
and to first order in G we have:
$$\displaystyle \begin{aligned} \begin{array}{rcl} \Gamma^i_{00} &\displaystyle =&\displaystyle g_{i0,0} - \frac 12 g_{00,i} \\ \Gamma^i_{0j} &\displaystyle =&\displaystyle \frac 12 (g_{i0,j} + g_{ij,0} - g_{0j,i}) \\ \Gamma^i_{jk} &\displaystyle =&\displaystyle \frac 12 (g_{ij,k} + g_{ik,j} - g_{jk,i}) \\ \Gamma^0_{00} &\displaystyle =&\displaystyle - \frac 12 g_{00,0} \\ \Gamma^0_{0j} &\displaystyle =&\displaystyle - \frac 12 g_{00,j} \\ \Gamma^0_{jk} &\displaystyle =&\displaystyle - \frac 12 (g_{0j,k} + g_{0k,j} - g_{jk,0}) \, . \end{array} \end{aligned} $$
(11.3.10)
Inserting these Christoffel-symbols into the general geodesic equation the linearized geodesic equation (11.3.9) is derived.
To first order in G we can then replace $$\dot x^i/c$$ by n i and obtain the PM light-ray equation in the form
$$\displaystyle \begin{aligned} \begin{array}{rcl} {} &\displaystyle &\displaystyle c^{-2} \ddot x^i(t) =\ {1 \over 2} g_{00,i} - g_{0i,0} - {1 \over 2} g_{00,0} n^i - (g_{0i,j} - g_{0j,i}) n^j - g_{ij,0} n^j\\ &\displaystyle &\displaystyle \qquad \qquad - g_{00,j} n^i n^j - \left( g_{ik,j} - {1 \over 2} g_{kj,i} \right) n^j n^k + \left( {1 \over 2} g_{jk,0} - g_{0k,j} \right) n^i n^j n^k \, . \end{array} \end{aligned} $$
(11.3.11)
Let
$$\displaystyle \begin{aligned} D_i \equiv \partial_i + n^i \partial_{ct} = \partial_i + n^i \partial_0 \, . \end{aligned} $$
(11.3.12)

Lemma 11.3

For an arbitrary differentiable function F(ct, x) the following relation holds:
$$\displaystyle \begin{aligned} \left[ D_i F(ct,{\mathbf{x}}) \right]_{{\mathbf{x}} = {\mathbf{x}}_{\mathrm{N}}} = \left( \hat \partial_i + n^i \partial_s \right) F[s, {\mathbf{n}} s + {\mathbf{d}}] \, . \end{aligned} $$
(11.3.13)

with x N = x 0 + n c(t − t 0). Here, d = x 0 −n(n ⋅x 0) is again the vector pointing from the origin of Σ x to the point of closest approach of the unperturbed light-ray. In (11.3.13) we assumed the components of d to be independent, so the operator $$\hat \partial _i$$ appears instead of $$\partial ^\perp _i$$ . Relation (11.3.13) has to be understood in the following way: in the left hand side one has to differentiate first before one makes the substitution; on the right hand side one first has to replace ct by s and x by n s + d and then the differentials have to be computed. Equation (11.3.13) generalizes the relation $$\partial _i = \partial ^\perp _i + n^i \partial _s$$ for the case that F is independent of t.

Proof

Since ct = s + ct ∗ and x N ≡x 0 + n c(t − t 0) = n s + d the proof follows from the identity
$$\displaystyle \begin{aligned} \left[ D_i F(ct,{\mathbf{x}}) \right]_{{\mathbf{x}}_{\mathrm{N}}} = (\partial^\perp_i + n^i \partial_s) F(s + ct^*, {\mathbf{n}} s + {\mathbf{d}}) \, . \end{aligned} $$
(11.3.14)
Using (11.3.13) and replacing the derivatives of the metric tensor by those of $$\tilde h_{\mu \nu }$$ the light-ray equation (11.3.11) can be written in the form (Kopeikin et al. 1999)
$$\displaystyle \begin{aligned} c^{-2} \ddot x^i(t) = {\frac 12} n_\alpha n_\beta \hat \partial_i \tilde h^{\alpha\beta} - \partial_s \left[n_\alpha \tilde h^{\alpha i} + {\frac 12} n^i \tilde h^{00} - {\frac 12} n^i n_p n_q \tilde h^{pq}\right] \, , \end{aligned} $$
(11.3.15)
where n α ≡ (1, n i) and all metric components on the right-hand-side have to be considered as functions of s and d (we wrote $$\hat \partial _i$$ instead of $$\partial _i^\perp $$ so that (11.2.13) can be used).
Let
$$\displaystyle \begin{aligned} \begin{aligned} B^{\alpha\beta}(s,{\mathbf{d}}) =\ & \int_{-\infty}^s \tilde h^{\alpha\beta} [\sigma,{\mathbf{d}}] \, d\sigma \\ D^{\alpha\beta}(s,{\mathbf{d}}) =\ & \int_{-\infty}^s B^{\alpha\beta} (\sigma,{\mathbf{d}}) \, d\sigma \, , \end{aligned} \end{aligned} $$
(11.3.16)
where σ is a parameter along x N equivalent to s so that B αβ and D αβ have the dimensions of a length and a length squared. A new integration parameter ζ is then defined to be equivalent to the retarded instance of time by the relation
$$\displaystyle \begin{aligned} \zeta + \vert {\mathbf{n}} \sigma + {\mathbf{d}} - {\mathbf{x}}_{\mathrm{A}}(\zeta) \vert = \sigma + c t^* \, . \end{aligned} $$
(11.3.17)
Equation (11.3.17) presents a relation between the time variables σ and ζ and the parameters t ∗, d and n. Taking the differentials of (11.3.17) we obtain
$$\displaystyle \begin{aligned} d\zeta (r_{\mathrm{A}} - {\boldsymbol{\beta}}_{\mathrm{A}} \cdot {\mathbf{r}}_{\mathrm{A}}) = d\sigma (r_{\mathrm{A}} - {\mathbf{n}} \cdot {\mathbf{r}}_{\mathrm{A}}) + r_{\mathrm{A}} c \, dt^* - {\mathbf{r}}_{\mathrm{A}} \cdot d{\mathbf{d}} - \sigma {\mathbf{r}}_{\mathrm{A}} \cdot d{\mathbf{n}} \, , \end{aligned} $$
(11.3.18)
where the coordinate position, x A, and velocity, v A, of body A should be taken at retarded time ζ and the coordinates of the photon, x γ, are taken at σ(ζ). Along the world-line of a photon we get (dt ∗ = d d = d n = 0)
$$\displaystyle \begin{aligned} d\sigma = d\zeta \ {r_{\mathrm{A}} - {\boldsymbol{\beta}}_{\mathrm{A}} \cdot {\mathbf{r}}_{\mathrm{A}} \over r_{\mathrm{A}} - {\mathbf{n}}_{\mathrm{A}} \cdot {\mathbf{r}}_{\mathrm{A}} } \, , \end{aligned} $$
(11.3.19)
so that the integrals for B αβ and D αβ take the form (dropping a summation over the various bodies labelled by A)
$$\displaystyle \begin{aligned} \begin{aligned} B^{\alpha\beta}(s) =\ & {4 G \over c^4} \int_{-\infty}^s d\zeta \ {\hat T^{\alpha\beta}(\zeta) - (1/2) \eta^{\alpha\beta} \hat T^\lambda_\lambda (\zeta) \over r_{\mathrm{A}}(\sigma,\zeta) - {\mathbf{n}} \cdot {\mathbf{r}}_{\mathrm{A}}(\sigma,\zeta) } \, , \\ D^{\alpha\beta}(s) =\ & \int_{-\infty}^s d\sigma \ B^{\alpha\beta}[\zeta(\sigma)] \, . \end{aligned} \end{aligned} $$
(11.3.20)
The photon trajectory is then described by
$$\displaystyle \begin{aligned} \begin{aligned} \dot x^i(s) =\ & c n^i + c \dot \Xi (s) \\ x^i(s) =\ & x_{\mathrm{N}}^i (s) + (\Xi^i(s) - \Xi^i(s_0)) \, \end{aligned} \end{aligned} $$
(11.3.21)
where s and s 0 correspond, respectively, to the moments of observation and emission of the photon. The functions $$\dot \Xi ^i(s)$$ and Ξi(s) are given by
$$\displaystyle \begin{aligned} \begin{aligned} \dot \Xi(s) =\ & {1 \over 2} n_\alpha n_\beta \hat\partial_i B^{\alpha\beta}(s) - n_\alpha \tilde h^{\alpha i} (s) \\ & - {1 \over 2} n^i \tilde h^{00}(s) + {1 \over 2} n^i n_p n_q \tilde h^{pq}(s) \, , \\ \Xi^i(s) =\ &{1 \over 2} n_\alpha n_\beta \hat\partial_i D^{\alpha\beta}(s) - n_\alpha B^{\alpha i} (s) \\ & - {1 \over 2} n^i B^{00}(s) + {1 \over 2} n^i n_p n_q B^{pq}(s) \end{aligned} \end{aligned} $$
(11.3.22)
with
$$\displaystyle \begin{aligned} \begin{array}{rcl} \hat\partial_i B^{\alpha\beta}(s) = - {4 G \over c^4} {\hat T^{\alpha\beta}(s) - (1/2) \eta^{\alpha\beta} \hat T^\lambda_\lambda(s) \over r_{\mathrm{A}} (s) - {\mathbf{n}} \cdot {\mathbf{r}}_{\mathrm{A}}(s)} \, {P^i_j r_{\mathrm{A}}^j(s) \over r_{\mathrm{A}}(s) - {\mathbf{v}}_{\mathrm{A}}(s) \cdot {\mathbf{r}}_{\mathrm{A}}(s)}\qquad \end{array} \end{aligned} $$
(11.3.23)
and
$$\displaystyle \begin{aligned} \begin{array}{rcl} \hat\partial_i D^{\alpha\beta}(s) &\displaystyle =&\displaystyle \int_{-\infty}^s \, \hat \partial_i B^{\alpha\beta} [\zeta(\sigma)] \, d\sigma \\ &\displaystyle =&\displaystyle - {4 G \over c^4} \int_{-\infty}^s \, {\hat T^{\alpha\beta}(\zeta) - (1/2) \eta^{\alpha\beta} \hat T^\lambda_\lambda(\zeta) \over [r_{\mathrm{A}} (\sigma,\zeta) - {\mathbf{n}} \cdot {\mathbf{r}}_{\mathrm{A}}(\sigma,\zeta)]^2} \, P^i_j r_{\mathrm{A}}^j(\sigma,\zeta)\, d\zeta \, . \end{array} \end{aligned} $$
(11.3.24)
From this we see that D αβ enters the expression for the gravitational light bending but not the gravitational time delay. Also $$\hat \partial _i B^{\alpha \beta }(s)$$ is not an integral but instantaneous function of time that can be calculated directly if the motion of the gravitational bodies is given (Kopeikin and Schäfer 1999). For more explicit expressions of x i(s) and $$\dot x^i(s)$$ see Klioner (2003b) and Zschocke (2018b).

11.3.1 The Shapiro Time Delay

From (11.3.21) we get
$$\displaystyle \begin{aligned} c (t - t_0) = \vert {\mathbf{x}} - {\mathbf{x}}_0 \vert + \Delta(t,t_0) \end{aligned}$$
with
$$\displaystyle \begin{aligned} \Delta(t,t_0) = {1 \over 2} n_\alpha n_\beta B^{\alpha\beta}(s) - {1 \over 2} n_\alpha n_\beta B^{\alpha\beta} (s_0) \, . \end{aligned} $$
(11.3.25)
For a single gravitating body A we get
$$\displaystyle \begin{aligned} \Delta_{\mathrm{A}}(t,t_0) = {2 G \over c^4} n_\alpha n_\beta \int_{s_0}^s d\zeta \ {\hat T^{\alpha\beta}(\zeta) - (1/2) \eta^{\alpha\beta} \hat T^\lambda_\lambda (\zeta) \over r_{\mathrm{A}}(\zeta) - {\mathbf{n}} \cdot {\mathbf{r}}_{\mathrm{ A}}(\zeta)} \, . \end{aligned} $$
(11.3.26)
Using expressions (11.3.2) for $$\hat T^{\alpha \beta }$$ we get
$$\displaystyle \begin{aligned} n_\alpha n_\beta \left( \hat T^{\alpha\beta} - (1/2) \eta^{\alpha\beta} \hat T^\lambda_\lambda \right) = \gamma_{\mathrm{A}} M_{\mathrm{A}} c^2 (1 - {\mathbf{n}} \cdot {\boldsymbol{\beta}}_{\mathrm{A}})^2 \end{aligned} $$
(11.3.27)
and
$$\displaystyle \begin{aligned} r_{\mathrm{A}}(\zeta) - {\mathbf{n}} \cdot {\mathbf{r}}_{\mathrm{A}}(\zeta) = ct^* + {\mathbf{n}} \cdot {\mathbf{x}}_{\mathrm{ A}}(\zeta) - \zeta \end{aligned} $$
(11.3.28)
so that
$$\displaystyle \begin{aligned} \Delta_{\mathrm{A}}(t,t_0) = {2 G M_{\mathrm{A}} \over c^2} \int_{s_0}^s {(1 - {\mathbf{n}} \cdot {\boldsymbol{\beta}}_{\mathrm{A}}(\zeta))^2 \over \sqrt{1 - \beta_{\mathrm{A}}^2(\zeta)}} \, {d\zeta \over ct^* + {\mathbf{n}} \cdot {\mathbf{x}}_{\mathrm{A}} (\zeta) - \zeta} \, . \end{aligned} $$
(11.3.29)
Let
$$\displaystyle \begin{aligned} y \equiv c t^* + {\mathbf{n}} \cdot {\mathbf{x}}_{\mathrm{A}}(\zeta) - \zeta = r_{\mathrm{A}}(\zeta) - {\mathbf{n}} \cdot {\mathbf{r}}_{\mathrm{A}}(\zeta) \end{aligned}$$
so that
$$\displaystyle \begin{aligned} dy = - (1 - {\mathbf{n}} \cdot {\boldsymbol{\beta}}_{\mathrm{A}}(\zeta)) \, d\zeta \end{aligned}$$
and
$$\displaystyle \begin{aligned} {d(\ln y) \over d\zeta} = {1 \over y} {dy \over d\zeta} = - {(1 - {\mathbf{n}} \cdot {\boldsymbol{\beta}} (\zeta)) \over ct^* + {\mathbf{n}} \cdot {\mathbf{x}}_{\mathrm{A}}(\zeta) - \zeta} \end{aligned}$$
and, therefore,
$$\displaystyle \begin{aligned} \Delta_{\mathrm{A}}(t,t_0) = - {2 G M_{\mathrm{A}} \over c^2} \int_{s_0}^s d\zeta \ {1 - {\mathbf{n}}\cdot {\boldsymbol{\beta}}_{\mathrm{A}}(\zeta) \over \sqrt{1 - \beta_{\mathrm{A}}^2 }} \, \left( {d (\ln y) \over d\zeta} \right) \, . \end{aligned}$$
Integration by parts then yields
../images/447007_1_En_11_Chapter/447007_1_En_11_Equ93_HTML.png
(11.3.30)
Since
$$\displaystyle \begin{aligned} {d \over d\zeta} \left[ {1 - {\mathbf{n}} \cdot {\boldsymbol{\beta}}_{\mathrm{A}}(\zeta) \over \sqrt{1 - \beta_{\mathrm{A}}^2(\zeta)}} \right] = - {1 \over (1 - \beta_{\mathrm{A}}^2)^{3/2} } [ {\mathbf{n}} - {\boldsymbol{\beta}}_{\mathrm{A}} - {\boldsymbol{\beta}}_{\mathrm{A}} \times ({\mathbf{n}} \times {\boldsymbol{\beta}}_{\mathrm{A}})] \, \dot {{\boldsymbol{\beta}}}_{\mathrm{A}} \end{aligned}$$
we finally obtain
../images/447007_1_En_11_Chapter/447007_1_En_11_Equ94_HTML.png
(11.3.31)
Neglecting all terms of order $$\beta _{\mathrm {A}}^2$$ this simplifies to
$$\displaystyle \begin{aligned} \begin{aligned} \Delta_{\mathrm{A}}(t,t_0) =\ & - {2 G M_{\mathrm{A}} \over c^2} \left[ \ln {r_{\mathrm{A}} - {\mathbf{n}} \cdot {\mathbf{r}}_{\mathrm{A}} \over r_{0{\mathrm{A}}} - {\mathbf{n}} \cdot {\mathbf{r}}_{0{\mathrm{A}}}} \right. \\ &- ({\mathbf{n}} \cdot {\boldsymbol{\beta}}_{\mathrm{A}}) \ln (r_{\mathrm{A}} - {\mathbf{n}} \cdot {\mathbf{r}}_{\mathrm{A}}) + ({\mathbf{n}} \cdot {\boldsymbol{\beta}}_{\mathrm{A}}) \ln (r_{0{\mathrm{A}}} - {\mathbf{n}} \cdot {\mathbf{r}}_{0{\mathrm{A}}}) \\ & + \left. \int_{s_0}^s d\zeta\ \ln (ct^* + {\mathbf{n}}\cdot {\boldsymbol{\beta}}_{\mathrm{A}} (\zeta) - \zeta) \, ({\mathbf{n}} \cdot \dot {{\boldsymbol{\beta}}}_{\mathrm{A}}(\zeta) ) \right]\, . \end{aligned} \end{aligned} $$
(11.3.32)
For a gravitating body A at rest at the origin of our coordinate system, x A(t) = 0, and using r −n ⋅x = r − s = d 2∕(r + s) , r 0 −n ⋅x 0 = r 0 − s 0 = d 2∕(r 0 + s) we recover our old result from (11.2.42)
$$\displaystyle \begin{aligned} \Delta_{\mathrm{A}}(t,t_0) = - 2 {G M_{\mathrm{A}} \over c^2} \ln {r - {\mathbf{n}} \cdot {\mathbf{x}} \over r_0 - {\mathbf{n}} \cdot {\mathbf{x}}_0} = + 2 {G M_{\mathrm{A}} \over c^2} \ln {r + s \over r_0 + s_0} \, . \end{aligned}$$

11.4 The Klioner-Formalism

A theory of astrometry at microarcsecond precision has been formulated by Klioner (2003). It was designed for practical applications, e.g., for the Gaia-mission. It covers not only the gravitational light deflection but also parallax, aberration and proper-motion of the light-sources. The Klioner-formalism is based upon five basic Euclidean unit vectors: s, m, σ, k, and l (Fig. 11.1).

  • s is the observed direction in the kinematically non-rotating local reference system of the observer,

  • m is the BCRS unit vector tangential to the light ray at the moment of observation,

  • σ is the BCRS unit vector tangential to the light ray at t = −∞,

  • k is the BCRS unit vector from the source to the observer and

  • l is the BCRS unit vector from the barycenter to the source.

This implies that for a light source at finite distance the emitted light ray is mathematically extended to past (timelike) infinity, such that the vector σ is well defined. High-precision astrometry can then be described by means of four consecutive transformations: s →m →σ →k →l.
../images/447007_1_En_11_Chapter/447007_1_En_11_Fig1_HTML.png
Fig. 11.1

The five basic vectors in the formalism of high-precision astrometry (Image credit: Klioner 2003)

11.4.1 Relativistic Aberration

The transformation from s to m accounts for relativistic aberration ; it reads:
$$\displaystyle \begin{aligned} {\mathbf{s}} = \left[ {\mathbf{s}}' + \tilde \gamma \tilde{\boldsymbol{\upbeta}} + (\tilde\gamma - 1) (\tilde{\boldsymbol{\upbeta}} \cdot {\mathbf{s}}') \tilde{\boldsymbol{\upbeta}}/\tilde{\boldsymbol{\upbeta}}^{2} \right] \cdot \frac{1 }{ \tilde\gamma (1 + \tilde{\boldsymbol{\upbeta}} \cdot {\mathbf{s}}') } {} \end{aligned} $$
(11.4.1)
where s ′ = −m, $$\tilde \gamma = (1 - \tilde {\boldsymbol {\upbeta }}^{2}/c^2)^{-1/2}$$ , $$\tilde {\boldsymbol {\upbeta }} = ({\mathbf {v}}_{\mathrm {obs}}/c)\left ( 1 + 2 w({\mathbf {x}}_{\mathrm {obs}})/c^2 \right )$$ , x obs and v obs are the BCRS position and velocity of the observer. Note, that both vectors, s and s ′, are Euclidean unit vectors.

Exercise 11.3

Use formula (11.4.1) to calculate the Euclidean scalar product s 1 ⋅s 2 for the non-gravitational case of SRT. Show that the result agrees with $$\cos \theta $$ from (5.​5.​13) with s i = −n i (γ 2 β 2 = γ 2 − 1).

11.4.2 Gravitational Light Deflection

A second transformation m →σ accounts for the gravitational light deflection for remote sources. Considering only one mass-monopole with
../images/447007_1_En_11_Chapter/447007_1_En_11_Equu_HTML.png
and one remote star that is observed the BCRS-metric leads to the following post-Newtonian result for the gravitational light deflection:
../images/447007_1_En_11_Chapter/447007_1_En_11_Equ97_HTML.png
(11.4.2)
with
$$\displaystyle \begin{aligned} {\mathbf{d}} = \boldsymbol{\upsigma} \times ({\mathbf{x}}_e \times \boldsymbol{\upsigma})\, . \end{aligned}$$
A third transformation, from σ to k,
$$\displaystyle \begin{aligned} \boldsymbol{\sigma} = {\mathbf{k}} + \frac{2 m }{ d^2} \, {\mathbf{d}} (\vert {\mathbf{x}}_{\mathrm{obs}} \vert - \vert {\mathbf{x}}_e \vert + \vert {\mathbf{x}}_{\mathrm{obs}} - {\mathbf{x}}_e \vert) \end{aligned} $$
(11.4.3)
accounts for the gravitational light deflection for light sources located inside the solar system (Klioner 2003). Here, x obs is the BCRS vector of the observer and x e that of the emission point.

11.4.3 Parallax

The fourth transformation, from k to l, describes the parallax . Let (t e, x e) and (t obs, x obs) be the BCRS coordinates of the events of emission and observation, R = x obs(t obs) −x e(t e); then k and l are defined as
$$\displaystyle \begin{aligned} {\mathbf{k}} = \mathbf{R}/\vert \mathbf{R} \vert \, , \qquad {\mathbf{l}} = {\mathbf{x}}_{\mathrm{e}}(t_{\mathrm{e}})/\vert {\mathbf{x}}_{\mathrm{e}}(t_{\mathrm{e}}) \vert \, . \end{aligned}$$
The relation between k and l is:
$$\displaystyle \begin{aligned} {\mathbf{k}} = \eta( - {\mathbf{l}} + \boldsymbol{\Uppi}) \end{aligned} $$
(11.4.4)
with
$$\displaystyle \begin{aligned} \eta = \frac{\vert {\mathbf{x}}_e \vert }{ \vert \mathbf{R}\vert} = \vert - {\mathbf{l}} + \boldsymbol{\Uppi} \vert^{-1} \, . \end{aligned}$$
Here,
$$\displaystyle \begin{aligned} \boldsymbol{\Uppi} (t_{\mathrm{obs}}) = \pi(t_{\mathrm{obs}}) \frac{ {\mathbf{x}}_{\mathrm{obs}}(t_{\mathrm{obs}})}{\mathrm{AU} } \, , \end{aligned}$$
where AU is the Astronomical Unit and the parallax of the source, π(t obs), is defined as
$$\displaystyle \begin{aligned}\pi (t_{\mathrm{obs}}) = \frac{\,\mathrm{AU}}{ \vert {\mathbf{x}}_e(t_{\mathrm{e}}) \vert} \, , \end{aligned}$$
so that
$$\displaystyle \begin{aligned} \boldsymbol{\Uppi} = \frac{{\mathbf{x}}_{\mathrm{obs}} (t_{\mathrm{obs}}) }{ \vert {\mathbf{x}}_e(t_e)\vert } \, . \end{aligned}$$

Exercise 11.4

Show that to second order in |Π| the expression for k can be written in the form
$$\displaystyle \begin{aligned} {\mathbf{k}} = - {\mathbf{l}} \left( 1 - \frac{1}{2} \vert \boldsymbol{\uppi} \vert^2 \right) + \boldsymbol{\uppi} (1 + {\mathbf{l}} \cdot \boldsymbol{\Uppi}) + \mathcal{O}(\vert\boldsymbol{\pi}\vert^3) \end{aligned}$$
with
$$\displaystyle \begin{aligned} \boldsymbol{\uppi} = {\mathbf{l}} \times (\boldsymbol{\Uppi} \times {\mathbf{l}}) \, . \end{aligned}$$
Show first that
$$\displaystyle \begin{aligned} \eta = (1 - 2 \boldsymbol{\Uppi} \cdot {\mathbf{l}} + \boldsymbol{\Uppi}^2)^{-1/2} \simeq 1 + \boldsymbol{\Uppi} \cdot {\mathbf{l}} - \frac{1 }{ 2} \boldsymbol{\Uppi}^2 + \frac{3 }{ 2} (\boldsymbol{\Uppi} \cdot {\mathbf{l}})^2 \, . \end{aligned}$$

11.4.4 Proper Motion and Radial Velocity

To describe proper motion and the radial velocity of the light source, one might employ a simple model for its space motion in BCRS coordinates (e.g., Klioner 2003):
$$\displaystyle \begin{aligned} {\mathbf{x}}_e(t_e) = {\mathbf{x}}_e(t_e^0) + {\mathbf{v}} \Delta t_e \, , \end{aligned} $$
(11.4.5)
where $$\Delta t_e = t_e - t_e^0$$ and v is the BCRS velocity of the source at $$t_e^0$$ . Here, $$t_e^0$$ corresponds to some initial epoch of observation $$t_{\mathrm {obs}}^0$$ . If t e denotes the emission time of a certain photon we have to sufficient approximation
$$\displaystyle \begin{aligned} c(t_{\mathrm{obs}} - t_e) = \vert {\mathbf{x}}_{\mathrm{obs}}(t_{\mathrm{obs}}) - {\mathbf{x}}_e(t_e) \vert \, . \end{aligned} $$
(11.4.6)
For some fictitious observer at the barycenter, B, one has
$$\displaystyle \begin{aligned} c(t_{\mathrm{B}} - t_e) = \vert {\mathbf{x}}_e(t_e)\vert \, . \end{aligned} $$
(11.4.7)
From the last two equations we can derive a relation between t obs and t B:
$$\displaystyle \begin{aligned} \begin{aligned} t_{\mathrm{B}} &= t_{\mathrm{obs}} + \frac{\vert {\mathbf{x}}_e(t_e) \vert - \vert {\mathbf{x}}_e(t_e) - {\mathbf{x}}_{\mathrm{obs}}(t_{\mathrm{obs}}) \vert }{ c}\\ &\simeq t_{\mathrm{obs}} + \frac{1 }{ c} \, {\mathbf{l}}\cdot {\mathbf{x}}_{\mathrm{obs}}(t_{\mathrm{obs}}) \, . \end{aligned} \end{aligned} $$
(11.4.8)
Let $$t_{\mathrm {B}}^0$$ be the reference epoch for some astrometric catalog, then the corresponding emission time, $$t_e^0$$ is given by
$$\displaystyle \begin{aligned} c\left(t_{\mathrm{B}}^0 - t_e^0\right) = \left|{\mathbf{x}}_e\left(t_e^0\right)\right| \, . \end{aligned} $$
(11.4.9)
In the XV-representation the source position is written in the form (11.4.5). The problem is to get a suitable representation for Δt e. From (11.4.6) to (11.4.9) we get
$$\displaystyle \begin{aligned} \Delta t_e = t_e - t_e^0 = t_{\mathrm{obs}} - t_{\mathrm{B}}^0 + \frac{1 }{ c} \, {\mathbf{l}} \cdot {\mathbf{x}}_{\mathrm{obs}}\left(t_{\mathrm{obs}}\right) + \frac{1 }{ c} \left(\left| {\mathbf{x}}_e\left(t_e^0\right) \right| - \left| {\mathbf{x}}_e\left(t_e\right) \right|\right) \end{aligned}$$
and the last term is (to first order in v) given by − c −1(l 0 ⋅v) Δt e, where l 0 refers to time $$t_e^0$$ , so that finally
$$\displaystyle \begin{aligned} \Delta t_e \simeq \frac{\tau }{ 1 + {\mathbf{l}}_0 \cdot {\mathbf{v}}/c } \end{aligned} $$
(11.4.10)
with
$$\displaystyle \begin{aligned} \tau = t_{\mathrm{obs}} - t_{\mathrm{B}}^0 + \frac{1 }{ c} \, {\mathbf{l}} \cdot {\mathbf{x}}_{\mathrm{obs}}(t_{\mathrm{obs}}) \, . \end{aligned} $$
(11.4.11)
The source’s BCRS spatial coordinates are then given by
$$\displaystyle \begin{aligned} {\mathbf{x}}_e(t_e) = {\mathbf{x}}_e (t_e^0) + {\mathbf{v}}_{\mathrm{app}} \, \tau \, , \end{aligned} $$
(11.4.12)
where the apparent source velocity, v app, is given by
$$\displaystyle \begin{aligned} {\mathbf{v}}_{\mathrm{app}} \equiv \frac{{\mathbf{v}} }{ 1 + {\mathbf{l}}_0 \cdot {\mathbf{v}}/c } \, . \end{aligned} $$
(11.4.13)
In the XV-representation the six quantities $${\mathbf {x}}_e(t_e^0)$$ and v are used to characterize the source position. By inserting (11.4.5) in to the definition for l and π(t obs) we obtain
$$\displaystyle \begin{aligned} {\mathbf{l}} = {\mathbf{l}}_0 + \dot{{\mathbf{l}}}_0 \, \Delta t_e \, , \qquad \pi(t_{\mathrm{obs}}) = \pi_0 + {\dot\pi}_0 \, \Delta t_e \, . \end{aligned} $$
(11.4.14)
Expressions for l 0 and π 0 are given below; expressions for $$\dot {{\mathbf {l}}}_0$$ and $${\dot \pi }_0$$ can be found in Klioner (2003b).
In the PPM-representation (parallax and proper motion) one employs the following quantities referring to some reference epoch $$t_{\mathrm {B}}^0$$ :

  • α 0 (right ascension )

  • δ 0 (declination )

  • π 0 (parallax)

  • μ α0 (apparent proper motion in α)

  • μ δ0 (apparent proper motion in δ)

  • μ r0 (apparent radial velocity times parallax over 1 AU).

Then,
$$\displaystyle \begin{aligned} {\mathbf{l}}_0 = \frac{{\mathbf{x}}_e \left(t_e^0\right) }{\left| {\mathbf{x}}_e \left(t_e^0\right) \right|} = \begin{pmatrix} \cos \delta_0 \cos\alpha_0 \\ \cos \delta_0 \sin \alpha_0 \\ \sin \delta_0 \end{pmatrix} \, . \end{aligned} $$
(11.4.15)
Defining
$$\displaystyle \begin{aligned} \boldsymbol{\upmu} \equiv {\mathbf{v}}_{\mathrm{app}} \frac{\pi_0 }{\mathrm{AU}} \end{aligned} $$
(11.4.16)
with
$$\displaystyle \begin{aligned} \pi_0 \equiv \frac{\mathrm{AU} }{ \vert {\mathbf{x}}_e(t_e^0) \vert} \end{aligned}$$
we can decompose the space motion vector μ by using the following set of orthonormal vectors:
$$\displaystyle \begin{aligned} {\mathbf{e}}^0_{(r)} = {\mathbf{l}}_0 \, ; \quad {\mathbf{e}}^0_{(\alpha)} = \begin{pmatrix} - \sin\alpha_0 \\ + \cos\alpha_0 \\ 0 \end{pmatrix}\,; \quad {\mathbf{e}}^0_{(\delta)} = \begin{pmatrix} - \sin\delta_0\cos\alpha_0 \\ - \sin\delta_0 \sin\alpha_0 \\ \cos\delta_0 \end{pmatrix} \end{aligned} $$
(11.4.17)
in the form
$$\displaystyle \begin{aligned} \boldsymbol{\upmu} = \mu_{r0} {\mathbf{e}}^0_{(r)} + \mu_{\alpha0} {\mathbf{e}}^0_{(\alpha)} + \mu_{\delta0} {\mathbf{e}}^0_{(\delta)} \end{aligned} $$
(11.4.18)
with
$$\displaystyle \begin{aligned} \mu_{r0} = \boldsymbol{\upmu} \cdot {\mathbf{e}}^0_{(r)} \, ; \quad \mu_{\alpha0} = \boldsymbol{\upmu} \cdot {\mathbf{e}}^0_{(\alpha)} \, ; \quad \mu_{\delta0} = \boldsymbol{\upmu} \cdot {\mathbf{e}}^0_{(\delta)} \, . \end{aligned}$$
The last equations show how the six quantities from the PPM-representation can be obtained from $${\mathbf {x}}_e (t_e^0)$$ and v 0. If the PPM-quantities are given l 0 is obtained from (11.4.15) and $${\mathbf {x}}_e (t_e^0) = {\mathbf {l}}_0 (\mathrm {AU}/\pi _0)$$ ; μ is obtained from (11.4.18) giving the apparent space motion vector v app. Finally,
$$\displaystyle \begin{aligned} {\mathbf{v}}_0 \simeq \frac{{\mathbf{v}}_{\mathrm{app}} }{ 1 - {\mathbf{l}}_0 \cdot {\mathbf{v}}_{\mathrm{app}}/c } \, . \end{aligned} $$
(11.4.19)