
In this unit, you’ll learn a broader set of integration techniques. So far, you know how to do only a few types of integrals: polynomials, some trig functions, and logs. Now we’ll turn our attention to a set of integrals that result in inverse trigonometric functions. But first, we need to go over the derivatives of the inverse trigonometric functions. (You might want to refer back to Chapter 12 on derivatives of inverse functions.)
Suppose you have the equation sin y = x. If you differentiate both sides with respect to x, you get
cos y 
![]() = 1
= 1
Now divide both sides by cos y.
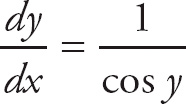
Because sin2 y + cos2 y = 1, we can replace cos y with 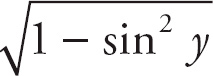
![]() .
.


Finally, because x = sin y, replace sin y with x. The derivative equals


Now go back to the original equation sin y = x and solve for y in terms of x: y = sin−1 x.
If you differentiate both sides with respect to x, you get

Replace 
![]() , and you get the final result.
, and you get the final result.


This is the derivative of inverse sine. By similar means, you can find the derivatives of all six inverse trig functions. They’re not difficult to derive, and they’re also not difficult to memorize. The choice is yours. We use u instead of x to account for the Chain Rule.


Notice the domain restrictions for inverse sine, cosine, secant, and cosecant.
Example 1: 

Example 2: 

Example 3:

 =
= 

Finding the derivatives of inverse trig functions is just a matter of following the formulas. They’re very rarely tested on the AP exam in this form and are not terribly important. In addition, the AP exam almost always tests only inverse sine and tangent, and then usually only as integrals, not as derivatives.
Therefore, it’s time to learn the integrals. The derivative formulas lead directly to the integral formulas, but because the only difference between the derivatives of inverse sine, tangent, and secant and those of inverse cosine, cotangent, and cosecant is the negative sign, only the former functions are generally used.


The first two always show up on the AP exam, so you should learn to recognize the pattern. Most of the time, the integration requires some sticky algebra to get the integral into the proper form.
Example 4: 

Don’t forget about u-substitution. Let u = x2 and du = 2x dx. Thus, 
![]() du = x dx. Substituting and integrating, we get
du = x dx. Substituting and integrating, we get


Now substitute back.

![]() sin− (x2) + C
sin− (x2) + C
Example 5: 

Anytime you see an integral where you have the square root of a constant minus a function, try to turn it into an inverse sine. You can do that here with a little simple algebra.


Now use u-substitution: let u = 
![]() and du =
and du = 
![]() dx, so 2du = dx, and substitute.
dx, so 2du = dx, and substitute.


When you substitute back, you get
sin− 
![]() + C
+ C
Example 6: 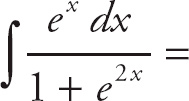
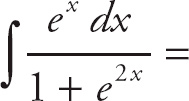
Again, use u-substitution. Let u = ex and du = ex dx, and substitute.

 = tan− u + C
= tan− u + CThen substitute back.
tan−1ex + C
Let’s do one last type that’s slightly more difficult. For this one, you need to remember how to complete the square.
Example 7: 
![]()
Complete the square in the denominator (your algebra teacher warned you about this).
x2 + 4x + 5 = (x + 2)2 + 1
Now rewrite the integral.
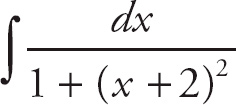
Using u-substitution, let u = x + 2 and du = dx. Then do the substitution.

 = tan− u + C
= tan− u + CWhen you put the function of x back in to the integral, it reads:
tan−1 (x + 2) + C
Evaluating these integrals involves looking for a particular pattern. If it’s there, all you have to do is use algebra and u-substitution to make the integrand conform to the pattern. Once that’s accomplished, the rest is easy. These integrals will show up again when we do partial fractions. Otherwise, as far as the AP exam is concerned, this is all you need to know.
Try these solved problems, and don’t forget to look for those patterns. Get out your index card, and cover the answers while you work.
PROBLEM 1. Find the derivative of y = sin−1 
![]() .
.
Answer: The rule is


The algebra looks like the following:
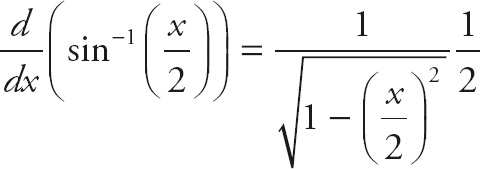
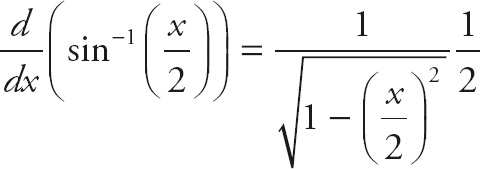
PROBLEM 2. Evaluate 
![]() .
.
Answer: First, you need to do a little algebra. Factor 4 out of the denominator.


Next, rewrite the integrand.


Now you can use u-substitution. Let u = 
![]() and du =
and du = 
![]() dx, so 2du = dx.
dx, so 2du = dx.
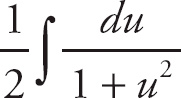
Now integrate it.

![]() tan−1 u + C
tan−1 u + C
And re-substitute.

![]() tan−1
tan−1 
![]() + C
+ C
PROBLEM 3. Evaluate 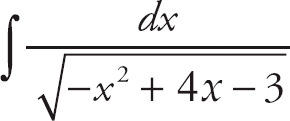
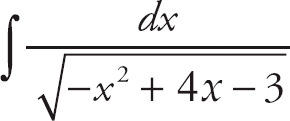 .
.
Answer: This time, you need to use some algebra by completing the square of the polynomial under the square root sign.
−x2 + 4x − 3 = −(x2 − 4x + 3) = −[(x − 2)2 − 1] = [1 − (x − 2)2]
Now rewrite the integrand.


And use u-substitution. Let u = x – 2 and du = dx.


Now, this looks familiar. Once you integrate, you get
sin−1 u + C
After you substitute back it becomes
sin−1 (x– 2) + C
Here is some more practice work on derivatives and integrals of inverse trig functions. The answers are in Chapter 23.
1. Find the derivative of 
![]() tan−1
tan−1
![]() .
.
2. Find the derivative of sin−1 
![]() .
.
3. Find the derivative of tan−1(ex).
4. Evaluate 
 .
.
5. Evaluate 
![]() .
.
6. Evaluate 
 .
.
7. Evaluate 
 .
.
8. Evaluate 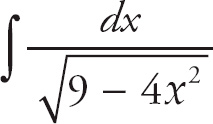
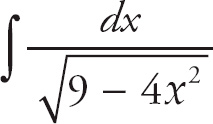 .
.
9. Evaluate 
 .
.
In Chapter 13, you learned how to find the integrals of some of the trigonometric functions. Now it’s time to figure out how to find the integrals of some of the more complicated trig expressions. First, recall some of the basic trigonometric integrals.


Some of these were derived by reversing differentiation, others by u-substitution.
Example 1: Evaluate 
![]() .
.
You can start by replacing sin2 x with 
![]() . This comes from taking the Double Angle formula cos 2x = 1 – 2 sin2 x and solving for sin2 x. After you make that replacement, the integral looks like the following:
. This comes from taking the Double Angle formula cos 2x = 1 – 2 sin2 x and solving for sin2 x. After you make that replacement, the integral looks like the following:

Remember the following substitution:
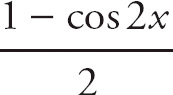
You could also use the following substitution:
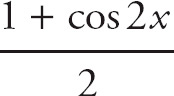
(Note: This comes from taking the Double Angle formula cos 2x = 2 cos2 x – 1 and solving for cos2 x.) You can also use the substitution to find 
![]() cos2 x dx.
cos2 x dx.
Now let’s do some variations.
Example 2: Evaluate 
![]() sin2 x cos x dx.
sin2 x cos x dx.
Here use some simple u-substitution. Let u = sin x and du = cos x dx and substitute.



When you substitute back, you get

 + C
+ C
In fact, you can do any integral of the form 
![]() sin2 x cos x dx using u-substitution, and the result will be
sin2 x cos x dx using u-substitution, and the result will be
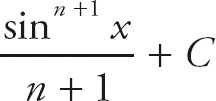
Similarly,


 + C
+ CHow about higher powers of sine and cosine?
Example 3: Evaluate 
![]() sin3 x dx.
sin3 x dx.
First, break the integrand into the following:

Next, using trig substitution, you get


You can turn the following into two integrals:


You can do both of these integrals.

 + C
+ CExample 4: Evaluate 
![]() sin3 x cos2 x dx.
sin3 x cos2 x dx.
Here, break the integrand into

Next, using trig substitution, you get


Now you can use u-substitution. Let u = cos x, du = –sin x dx, and substitute.

Now substitute back, and you’re done.


As you can see, these integrals all require you to know trig substitutions and u-substitution. The AP exam doesn’t ask too many variations on these integrals, but let’s do just a few other types, just in case.
Example 5: Evaluate 
![]() tan2 x dx.
tan2 x dx.
First, use the trigonometric substitution tan2 x = sec2 x – 1.


Now break this into two integrals that are easy to evaluate.


And integrate.
tan x – x + C
Example 6: Evaluate 
![]() tan3 x dx.
tan3 x dx.
Recognize what to do here? Right! Break up the integrand!

Next, use the trig substitution tan2 x = sec2 x – 1 in the expression.

Break this into two integrals.

Tackle the first integral using u-substitution. Let u = tan x and du = sec2 x dx.


Substituting back gives you

 + C
+ C
We’ve done the second integral before.

Thus, the integral is

 + ln |cos x| + C
+ ln |cos x| + CExample 7: Evaluate 
![]() sec3 x dx.
sec3 x dx.
Now it’s time for integration by parts. Let u = sec x and dv = sec2 x dx. Therefore, du = sec x tan x dx and v = tan x. Plug these into the formula, and you get

Next, substitute tan2 x = sec2 x – 1.

So, the integral has become
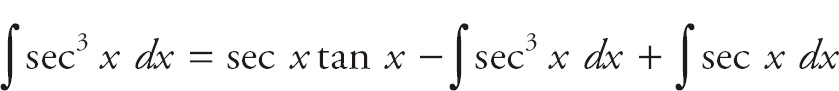
Now, add 
![]() sec3 x dx to both sides.
sec3 x dx to both sides.

Finally, recall that the integral on the right is
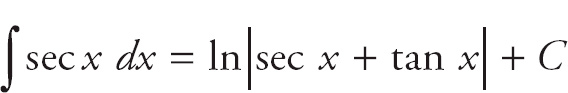
The combined integral is
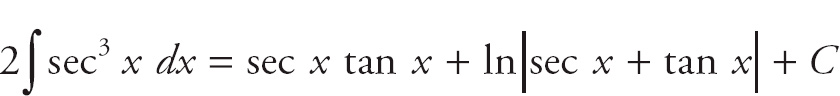
When you divide by 2, you get your final answer.


Whew! This is about as difficult as the AP exam ever gets. Believe it or not, trigonometric integrals can get even more complicated, involving higher powers or more difficult combinations of trig functions. Thankfully, the AP exam tends to limit itself to the simpler ones.
Walk yourself through the step-by-step process by trying some solved problems below. Cover each answer first, then check your answer.
PROBLEM 1. 
![]() cos2 x dx
cos2 x dx
Answer: Use the substitution 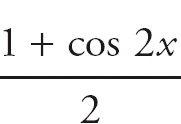
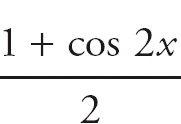 . Now the integral looks like the following:
. Now the integral looks like the following:


Divide this into two integrals.

When you evaluate each one separately, you get
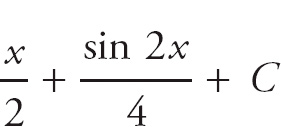
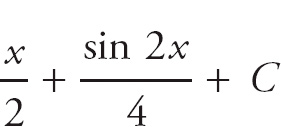
PROBLEM 2. 
![]() cos3 x dx
cos3 x dx
Answer: Here, split cos3 x into cos x cos2 x, and replace the second term with (1 – sin2 x).
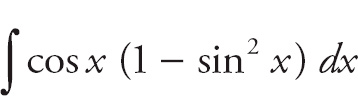
This can be rewritten as

The left-hand integral is sin x. Do the right-hand integral using u-substitution. Let u = sin x and du = cos x dx. You get

When you substitute back, the second integral becomes


Thus, the complete answer is


PROBLEM 3. 
 sec2 x dx
sec2 x dx
Answer: This won’t take long. Use u-substitution, by letting u = tan x and du = sec2 x dx.

The final result when you substitute back is

Evaluate the following integrals. The answers are in Chapter 23.