
Click here to download a PDF of Practice Test 3
At a Glance
Total Time
1 hour and 45 minutes
Number of Questions
45
Percent of Total Grade
50%
Writing Instrument
Pencil required
Section I of this examination contains 45 multiple-choice questions. Fill in only the ovals for numbers 1 through 45 on your answer sheet.
CALCULATORS MAY NOT BE USED IN THIS PART OF THE EXAMINATION.
Indicate all of your answers to the multiple-choice questions on the answer sheet. No credit will be given for anything written in this exam booklet, but you may use the booklet for notes or scratch work. After you have decided which of the suggested answers is best, completely fill in the corresponding oval on the answer sheet. Give only one answer to each question. If you change an answer, be sure that the previous mark is erased completely. Here is a sample question and answer.
Sample Question
Chicago is a
(A) state
(B) city
(C) country
(D) continent
(E) village
Sample Answer

Use your time effectively, working as quickly as you can without losing accuracy. Do not spend too much time on any one question. Go on to other questions and come back to the ones you have not answered if you have time. It is not expected that everyone will know the answers to all the multiple-choice questions.
Many candidates wonder whether or not to guess the answers to questions about which they are not certain. Multiple choice scores are based on the number of questions answered correctly. Points are not deducted for incorrect answers, and no points are awarded for unanswered questions. Because points are not deducted for incorrect answers, you are encouraged to answer all multiple-choice questions. On any questions you do not know the answer to, you should eliminate as many choices as you can, and then select the best answer among the remaining choices.
SECTION I, Part A
Time—55 Minutes
Number of questions—28
A CALCULATOR MAY NOT BE USED ON THIS PART OF THE EXAMINATION
Directions: Solve each of the following problems, using the available space for scratchwork. After examining the form of the choices, decide which is the best of the choices given and fill in the corresponding oval on the answer sheet. No credit will be given for anything written in the test book. Do not spend too much time on any one problem.
In this test: Unless otherwise specified, the domain of a function f is assumed to be the set of all real numbers x for which f(x) is a real number.
1. If y = tan(2πx), then 
![]() = ?
= ?
| (A) | cot(2πx) |
| (B) | 2πcot(2πx) |
| (C) | 2πsec2(2πx) |
| (D) |  |
| (E) | 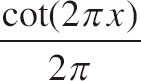 |
| (A) | 0 |
| (B) | 1 |
| (C) | −1 |
| (D) | ∞ |
| (E) | Does Not Exist |
3. 
![]() (5x − 1)4 dx =
(5x − 1)4 dx =
| (A) |  |
| (B) | 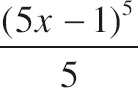 |
| (C) | (5x ‒ 1)3 + C |
| (D) | 25(5x ‒ 1)3 + C |
| (E) |  |
4. For 0 ≤ t ≤ 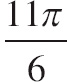
![]() , an object travels along the ellipse given by x = 2sin t, y = −3cos t. At t =
, an object travels along the ellipse given by x = 2sin t, y = −3cos t. At t = 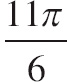
![]() , the object leaves the ellipse and travels along the line tangent to the path at that point. What is the slope of the tangent line at t =
, the object leaves the ellipse and travels along the line tangent to the path at that point. What is the slope of the tangent line at t = 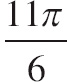
![]() ?
?
| (A) |  |
| (B) |  |
| (C) |  |
| (D) |  |
| (E) |  |
5. If f(x) = 
 , which of the following is true?
, which of the following is true?
| (A) | f(x) is continuous and differentiable at x = 2 |
| (B) | f(x) is not defined at x = 2 |
| (C) | f(x) is differentiable but not continuous at x = 2 |
| (D) | f(x) is continuous but not differentiable at x = 2 |
| (E) | f(x) is neither continuous nor differentiable at x = 2 |
6. 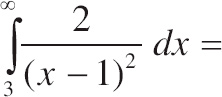
![]() =
=
| (A) |  |
| (B) | 8 |
| (C) |  |
| (D) | 1 |
| (E) | e2 |
7. The position of a particle at time t ≥ 0, in seconds, is given by x = 2t3 + 3t2 – 12t and y = 2t3 – 15t2 + 24t. At what values of t is the particle at rest?
| (A) | t = 1 |
| (B) | t = 1, 2, 4 |
| (C) | t = 2 |
| (D) | t = 2, −3 |
| (E) | t = −3, 1, 2, 4 |
8. 
![]() 3xcsc2x2dx =
3xcsc2x2dx =
| (A) |  |
| (B) |  |
| (C) | 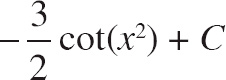 |
| (D) | 3sec2(x2) + C |
| (E) |  |
9. If f(x) = log5(x3 − x − 1), then f′(2) =
| (A) |  |
| (B) | 11 |
| (C) | e5 |
| (D) | 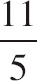 |
| (E) | Does Not Exist |
10. What is the value of 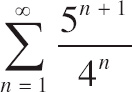
![]() ?
?
| (A) | 1 |
| (B) |  |
| (C) |  |
| (D) | 0 |
| (E) | Diverges |
11. If the MacLaurin series for ex is 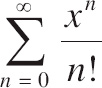
![]() , what is a power series expansion for
, what is a power series expansion for 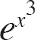
![]() ?
?
| (A) | 1 + x3 + x6 + x9 + … |
| (B) | 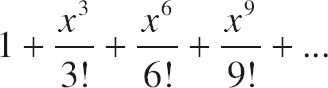 |
| (C) |  |
| (D) |  |
| (E) |  |
12. The rate of growth of algae, A, in a pond with respect to time, t, is directly proportional to one half the amount of algae in the pond. Which differential equation describes this relationship?
| (A) | A(t) =  |
| (B) | 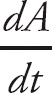  |
| (C) | 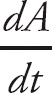 |
| (D) | 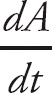   |
| (E) | 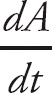  |


13. In the above graph of f(x), at which of the labelled points does the limit exist but the function exists and is not equal to the limit?
| (A) | a |
| (B) | b |
| (C) | c |
| (D) | d |
| (E) | e |
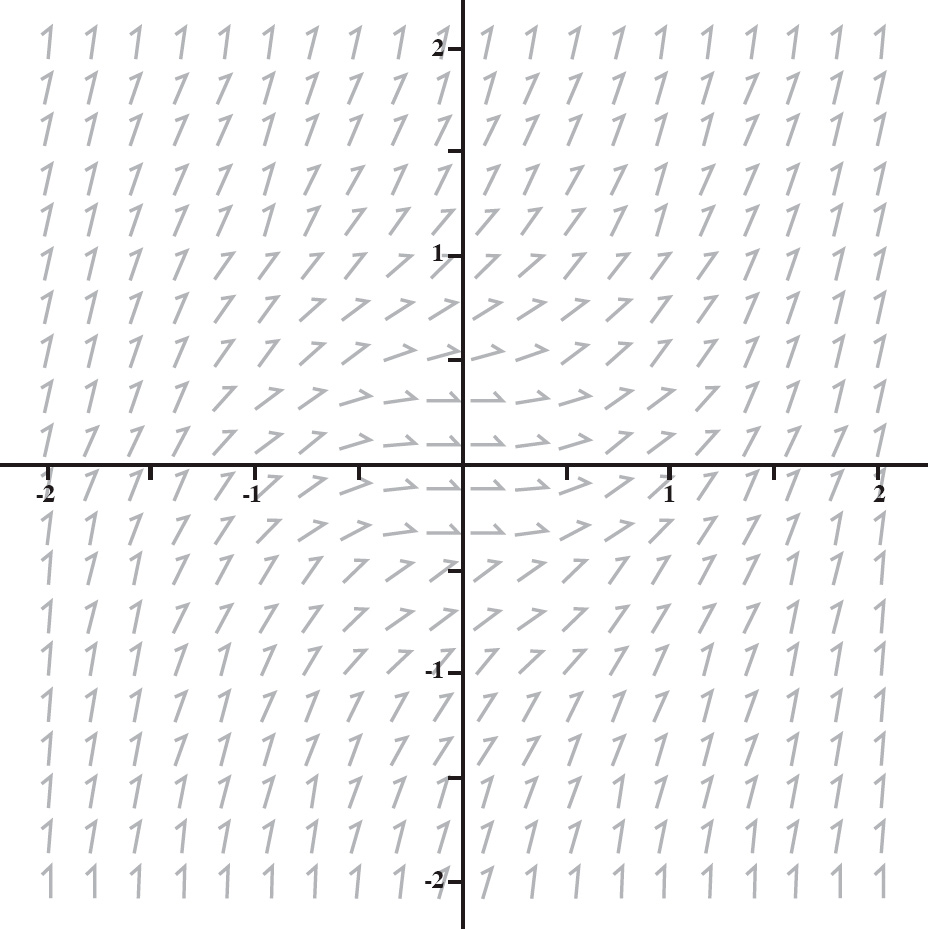

14. Which of the following is the differential equation of the slope field above?
| (A) |  |
| (B) |  |
| (C) |  |
| (D) |  |
| (E) |  |
15. The length of a curve from x = 2 to x = 3 is given by 
![]() . If the curve contains the point (2, 10), which of the following could be the curve?
. If the curve contains the point (2, 10), which of the following could be the curve?
| (A) | y = 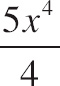 |
| (B) | y = 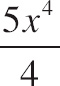 |
| (C) | y = (5x)3 − 990 |
| (D) | y = 25x2 − 90 |
| (E) | y = 25x3 + 10 |
16. If the line tangent to the graph of the function f at the point (8, 2) passes through the point (2, 5), then f′(8) =
| (A) | 2 |
| (B) | −2 |
| (C) |  |
| (D) | − |
| (E) | Does Not Exist |
17. A curve is defined by the parametric equations x = t3 + 2t − 1 and y = t2. Which of the following is an equation of the line tangent to the graph at (11, 4)?
| (A) | 7x ‒ 2y = 69 |
| (B) | 2y ‒ 7x = 69 |
| (C) | 7y ‒ 2x = 6 |
| (D) | 2x − 7y = 6 |
| (E) | 7x + 2y = 69 |
18. The graph of the function f is shown below
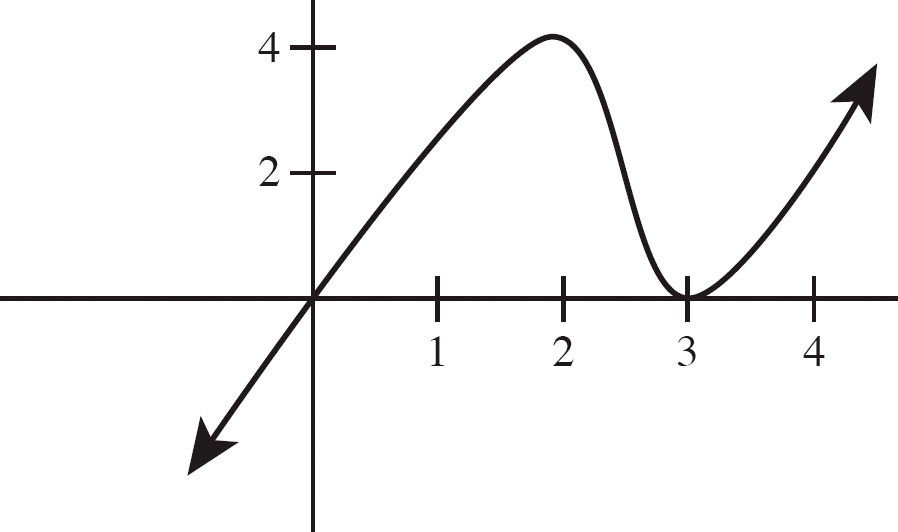

If g(x) = 
![]() f(t)dt, what is g′(2)?
f(t)dt, what is g′(2)?
| (A) | 32 |
| (B) | 16 |
| (C) | 8 |
| (D) | 4 |
| (E) | 0 |
19. If the graph of y = f(x) has slope 3x2 + 5 at each point (x,y) on the curve and it passes through (2, 18), which of the following is the equation of f(x)?
| (A) | y = 17x − 16 |
| (B) | y = x3 + 5x |
| (C) | y = 2x − 18 |
| (D) | y = x3 + 5x − 1 |
| (E) | y = 17x − 52 |
20. Which of the following are the first four nonzero terms of the MacLaurin series for f(x) = sin(x2)?
| (A) |  |
| (B) |  |
| (C) |  |
| (D) | 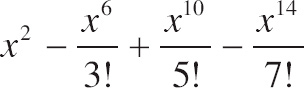 |
| (E) | 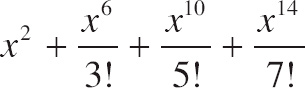 |
21. The number of new members of a social media site is modeled by the function y that satisfies the differential equation 
![]() ), where t is the time in days and y(0) = 100. What is
), where t is the time in days and y(0) = 100. What is 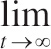
![]() y(t)?
y(t)?
| (A) | 100,000 |
| (B) | 25 |
| (C) | 2500 |
| (D) | 100 |
| (E) | 10,000 |
22. For what values of x does the series 
![]() converge?
converge?
| (A) | x > 5 |
| (B) | −  |
| (C) | x >  |
| (D) | ‒5 < x < 5 |
| (E) | All real numbers. |
| (A) | 6xe6x − 36e6x + C |
| (B) |  |
| (C) |  |
| (D) |  |
| (E) |  |
24. Which of the following series converge(s)?
| (I) |  |
| (II) | 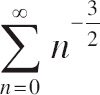 |
| (III) | 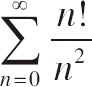 |
| (A) | I only |
| (B) | II only |
| (C) | I and II |
| (D) | II and III |
| (E) | They all converge |
25. The function f is continuous on the closed interval [0,10] and has the values in the following table:


Using the subintervals [0, 2], [2, 5], [5, 7], and [7, 10], approximate 
![]() f(x)dx using a left Riemann sum.
f(x)dx using a left Riemann sum.
| (A) | 102 |
| (B) | 204 |
| (C) | 176 |
| (D) | 242 |
| (E) | 665 |
26. 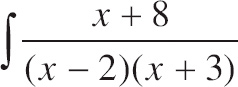
![]() dx =
dx =
| (A) | 2 ln|x − 2| − ln|x + 3| + C |
| (B) | 2 ln|x − 2| + ln|x + 3| + C |
| (C) | 2 ln|x − 2| + 8ln|x + 3| + C |
| (D) | ln |x2 + x − 6| − 8 + C |
| (E) | ln |x2 + x − 6| + 8 + C |
27. 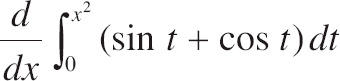
![]() :
:
| (A) | x2sin x2 − x2cos x2 |
| (B) | −2xcos x2 + 2xsin x2 |
| (C) | x2sin x2 + x2cos x2 |
| (D) | 2xsin x2 + 2xcos x2 |
| (E) |  |
28. What is the coefficient of x8 in the Taylor series for 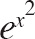
![]() about x = 0?
about x = 0?
| (A) | 24 |
| (B) |  |
| (C) |  |
| (D) |  |
| (E) | 6 |
END OF PART A, SECTION I
IF YOU FINISH BEFORE TIME IS CALLED, YOU MAY CHECK YOUR WORK ON PART A ONLY.
DO NOT GO ON TO PART B UNTIL YOU ARE TOLD TO DO SO.
SECTION I, Part B
Time—50 Minutes
Number of questions—17
A GRAPHING CALCULATOR IS REQUIRED FOR SOME QUESTIONS ON THIS PART OF THE EXAMINATION
Directions: Solve each of the following problems, using the available space for scratchwork. After examining the form of the choices, decide which is the best of the choices given and fill in the corresponding oval on the answer sheet. No credit will be given for anything written in the test book. Do not spend too much time on any one problem.
In this test:
(1) The exact numerical value of the correct answer does not always appear among the choices given. When this happens, select from among the choices the number that best approximates the exact numerical value.
(2) Unless otherwise specified, the domain of a function f is assumed to be the set of all real numbers x for which f(x) is a real number.
29. Let y = f(x) be the solution to 
![]() = 2x − y with f(1) = 5. Use Euler’s method to approximate f(3), starting at x = 1 with a step size of 0.5.
= 2x − y with f(1) = 5. Use Euler’s method to approximate f(3), starting at x = 1 with a step size of 0.5.
| (A) | −7.0 |
| (B) | 3.625 |
| (C) | 3.75 |
| (D) | 4.3125 |
| (E) | 3.84375 |
30. If P(x) = x − 2x2 + 3x4 − 4x6 is the sixth degree Taylor polynomial for the function f about x = 0, what is f′′(0)?
| (A) | −4 |
| (B) | 1 |
| (C) | 72 |
| (D) | −120 |
| (E) | −88 |
31. The side of a square is decreasing at a constant rate of 0.4 cm/s. What is the rate of decrease of the perimeter of the square when the area of the square is 16 m2?
| (A) | 3.2 m/s |
| (B) | 1.6 m/s |
| (C) | 1 m/s |
| (D) | −3.2 m/s |
| (E) | −1.6 m/s |
33. 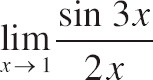
![]() =
=
| (A) | 0.026 |
| (B) | 0.071 |
| (C) | 1.500 |
| (D) | 3 |
| (E) | The limit does not exist |
34. Profits, in dollars, for a small business can be modeled by 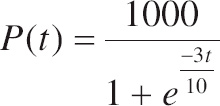
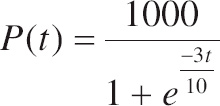 where t is measured in years. What are the total profits in years 5 ≤ t ≤ 8, to the nearest dollar?
where t is measured in years. What are the total profits in years 5 ≤ t ≤ 8, to the nearest dollar?
| (A) | $5,959 |
| (B) | $3,361 |
| (C) | $2,618 |
| (D) | $2,824 |
| (E) | $5,442 |
35. The position of a particle at any time t ≥ 0 is given by x(t) = 4cos 2t and y(t) = 3sin 4t. What is the particle’s speed at time t = 5 seconds?
| (A) | 6.551 |
| (B) | 12.848 |
| (C) | 8.393 |
| (D) | 21.313 |
| (E) | 1.638 |
36. What is the minimum value of f(x) = 2xe−x2 on the closed interval [‒1, 2]?
| (A) | −0.858 |
| (B) | −0.736 |
| (C) | 0.736 |
| (D) | 0.858 |
| (E) | 0.073 |
37. Which of the following integrals gives the area of the region enclosed by r = 3 ‒ 2cos 4θ on the closed interval 
![]() ?
?
| (A) |   |
| (B) |   |
| (C) | 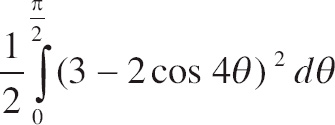 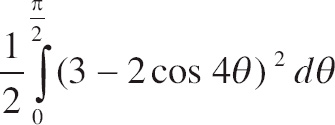 |
| (D) | 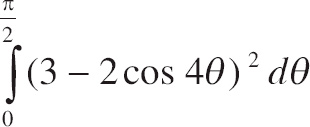 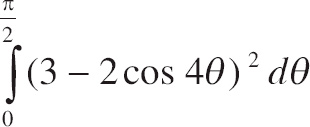 |
| (E) | 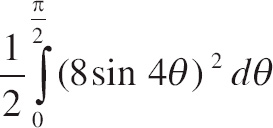 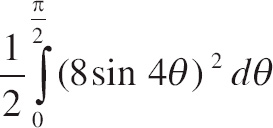 |
38. Use the Trapezoidal Sum to approximate 
![]() (3 + x + x2)dx using n = 4 subintervals.
(3 + x + x2)dx using n = 4 subintervals.
| (A) | 13.75 |
| (B) | 27.5 |
| (C) | 21.5 |
| (D) | 10.75 |
| (E) | 43.0 |
39. A particle moves along the x-axis so that its acceleration at any time t ≥ 0 is given by a(t) = 8sin 2t + 4cos 2t. If its initial velocity is 8 units/s and its initial position is x = 4, what is its position, in units, at time t = 2 seconds?
| (A) | 13.101 |
| (B) | 9.101 |
| (C) | 31.167 |
| (D) | 15.167 |
| (E) | 26.833 |
40. If f(x) = x2e4x, what is the x-coordinate of the maximum value of f on the closed interval [‒1, 0]?
| (A) |  |
| (B) | 2.128 |
| (C) | 2.356 |
| (D) | π |
| (E) | 1.571 |
| (A) | ‒e2xcos x + C |
| (B) | 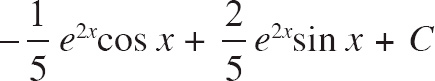 |
| (C) |  |
| (D) |  |
| (E) |  |
42. The region in the first quadrant bounded by y = 4x − x2 and the x-axis is revolved around the x-axis. What is the volume of the resulting solid?
| (A) | 16.755 |
| (B) | 53.617 |
| (C) | 33.510 |
| (D) | 34.133 |
| (E) | 107.233 |
43. What is the length of the curve f(x) = ln(x + 1) from x = 1 to x = 3?
| (A) | 2.250 |
| (B) | 1.870 |
| (C) | 1.614 |
| (D) | 2.121 |
| (E) | 2.320 |
44. Let f(x) = 3x − x3. What is the value of c on the closed interval [1, 3] that satisfies the conclusion of the Mean Value Theorem?
| (A) | −2.082 |
| (B) | 2 |
| (C) | 1.577 |
| (D) | 2.613 |
| (E) | 2.082 |
45. If f(x) = arctan x, what is the average value of f(x) on the closed interval 
![]() ?
?
| (A) | 20.620 |
| (B) | 0.167 |
| (C) | 16.195 |
| (D) | 0.360 |
| (E) | 0.283 |
STOP
END OF PART B, SECTION I
IF YOU FINISH BEFORE TIME IS CALLED, YOU MAY CHECK YOUR WORK ON PART B ONLY.
DO NOT GO ON TO SECTION II UNTIL YOU ARE TOLD TO DO SO.
SECTION II
GENERAL INSTRUCTIONS
You may wish to look over the problems before starting to work on them, since it is not expected that everyone will be able to complete all parts of all problems. All problems are given equal weight, but the parts of a particular problem are not necessarily given equal weight.
A GRAPHING CALCULATOR IS REQUIRED FOR SOME PROBLEMS OR PARTS OF PROBLEMS ON THIS SECTION OF THE EXAMINATION.
SECTION II, PART A
Time—30 minutes
Number of problems—2
A graphing calculator is required for some problems or parts of problems.
During the timed portion for Part A, you may work only on the problems in Part A.
On Part A, you are permitted to use your calculator to solve an equation, find the derivative of a function at a point, or calculate the value of a definite integral. However, you must clearly indicate the setup of your problem, namely the equation, function, or integral you are using. If you use other built-in features or programs, you must show the mathematical steps necessary to produce your results.
1. Let R be the region bounded by the graphs of y = 4 ln x, y = 
![]() , and x = 1, as shown in the figure below.
, and x = 1, as shown in the figure below.
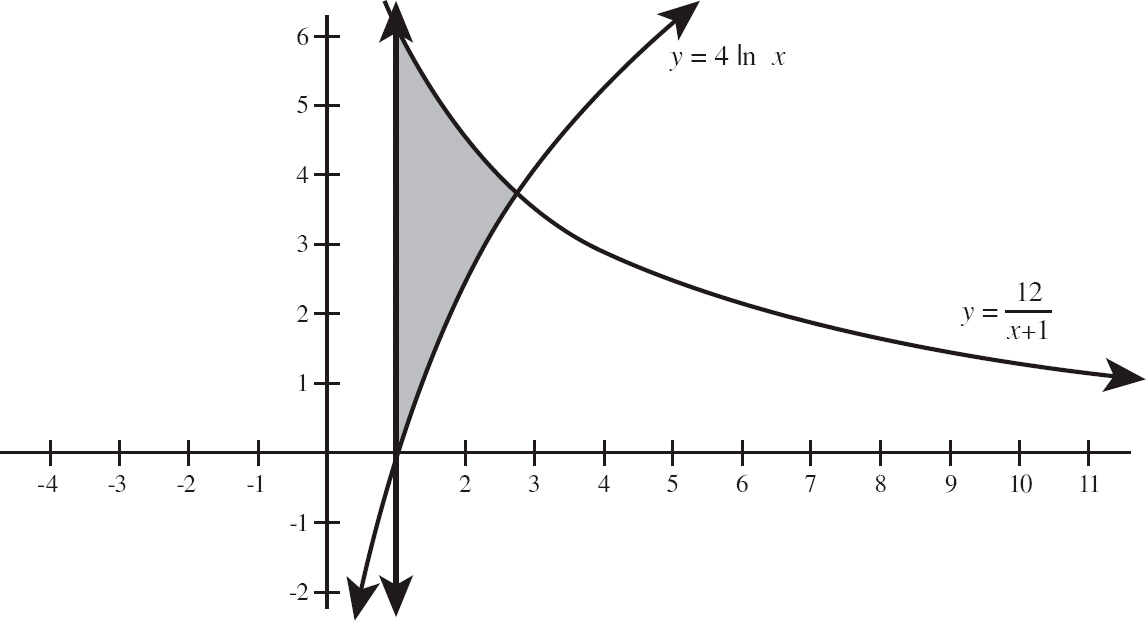

| (a) | Find the area of R. |
| (b) | Find the volume of the solid that results when R is revolved about the vertical line x = 1. |
| (c) | Let R be the base of a solid. Every cross-section of the solid perpendicular to the x-axis is an equilateral triangle with one side across the base. Find the volume of the solid. |
2. For t ≥ 0, a particle is moving along a curve with its position at time t given by (x(t), y(t)) and 
![]() = 3t2 − 4,
= 3t2 − 4, 
![]() = 2t. At time t = 1, its position is (−3, 1).
= 2t. At time t = 1, its position is (−3, 1).
| (a) | Find the slope of the particle’s path at time t = 3. |
| (b) | Find the x-coordinate of the particle’s position at time t = 5. |
| (c) | Find the speed of the particle at time t = 5. |
| (d) | Find the acceleration vector of the particle at time t = 5. |
SECTION II, PART B
Time—1 hour
Number of problems—4
No calculator is allowed for these problems.
During the timed portion for Part B, you may continue to work on the problems in Part A without the use of any calculator.
3. A water storage tank is in the shape of an inverted cone whose height is 16 meters and radius is 4 meters. The tank initially contains 36π m. The water is filling from the tank at a rate of 2πh m/min.
| (a) | Find  |
| (b) | If h = 12 m at time t = 0, find an equation for h as a function of t. |
| (c) | At what time is the storage tank full? |
4. The function f is differentiable everywhere erywhere and the MacLaurin series is 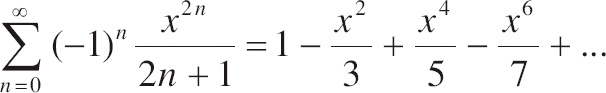
![]()
| (a) | Use the ratio test to find the interval of convergence of the MacLaurin series of f. |
| (b) | Approximate  |
| (c) | Write the first four nonzero terms and the general term for the MacLaurin series for f′(x) |
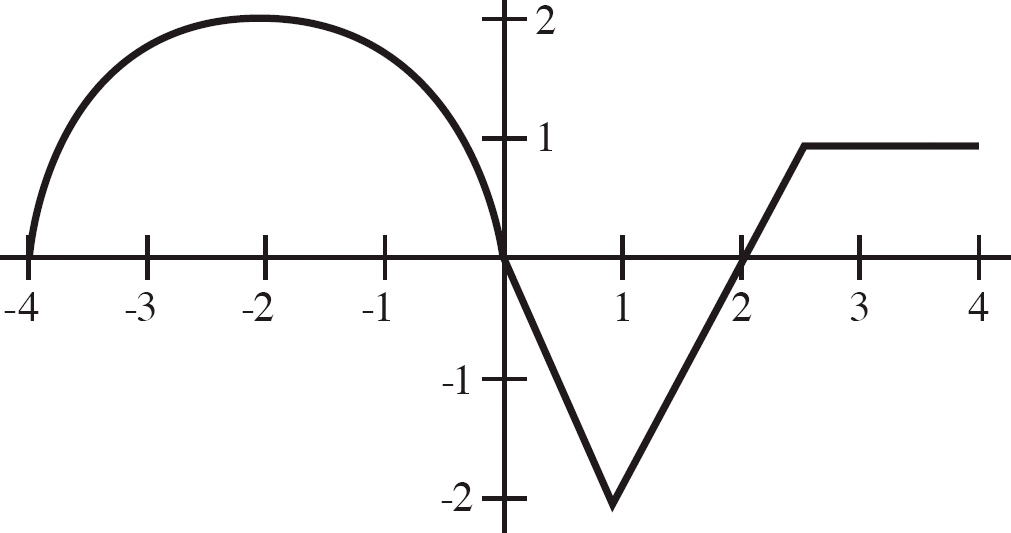

5. The figure above shows the graph of f, which is a continuous function defined on −4 ≤ x ≤ 4. The graph of f from x = −4 to x = 0 is a semi-circle, and from x = 0 to x = 4 consists of three line segments. Let g(x) = 
![]() f(t)dt.
f(t)dt.
| (a) | Find g(2) and g(−2). |
| (b) | Evaluate g′(1). |
| (c) | Evaluate Find all values of x where g(x) has a point of inflection. |
| (d) | At what value of x is g(x) a minimum? |
6. Bacteria is growing in a Petri dish at a rate that satisfies the differential equation 
![]() , where A is the number of bacteria and t is measured in days. There are initially 1200 bacteria in the dish.
, where A is the number of bacteria and t is measured in days. There are initially 1200 bacteria in the dish.
| (a) | Use the line tangent to the graph of A at t = 0 to estimate the number of bacteria the end of t = 5 days. |
| (b) | Find 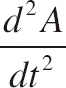 |
| (c) | Find the particular solution to the above differential equation with the initial condition A(0) = 1200. |
STOP
END OF EXAM