
Click here to download a PDF of Practice Test 1
At a Glance
Total Time
1 hour and 45 minutes
Number of Questions
45
Percent of Total Grade
50%
Writing Instrument
Pencil required
Section I of this examination contains 45 multiple-choice questions. Fill in only the ovals for numbers 1 through 45 on your answer sheet.
CALCULATORS MAY NOT BE USED IN THIS PART OF THE EXAMINATION.
Indicate all of your answers to the multiple-choice questions on the answer sheet. No credit will be given for anything written in this exam booklet, but you may use the booklet for notes or scratch work. After you have decided which of the suggested answers is best, completely fill in the corresponding oval on the answer sheet. Give only one answer to each question. If you change an answer, be sure that the previous mark is erased completely. Here is a sample question and answer.
Sample Question
Chicago is a
(A) state
(B) city
(C) country
(D) continent
(E) village
Sample Answer

Use your time effectively, working as quickly as you can without losing accuracy. Do not spend too much time on any one question. Go on to other questions and come back to the ones you have not answered if you have time. It is not expected that everyone will know the answers to all the multiple-choice questions.
Many candidates wonder whether or not to guess the answers to questions about which they are not certain. Multiple choice scores are based on the number of questions answered correctly. Points are not deducted for incorrect answers, and no points are awarded for unanswered questions. Because points are not deducted for incorrect answers, you are encouraged to answer all multiple-choice questions. On any questions you do not know the answer to, you should eliminate as many choices as you can, and then select the best answer among the remaining choices.
SECTION I, Part A
Time—55 Minutes
Number of questions—28
A CALCULATOR MAY NOT BE USED ON THIS PART OF THE EXAMINATION
Directions: Solve each of the following problems, using the available space for scratchwork. After examining the form of the choices, decide which is the best of the choices given and fill in the corresponding oval on the answer sheet. No credit will be given for anything written in the test book. Do not spend too much time on any one problem.
In this test: Unless otherwise specified, the domain of a function f is assumed to be the set of all real numbers x for which f(x) is a real number.
1. If 7 = xy – exy, then 
![]() =
=
| (A) | x – ey |
| (B) | y – ex |
| (C) |  |
| (D) |  |
| (E) |  |
2. The volume of the solid that results when the area between the curve y = ex and the line y = 0, from x = 1 to x = 2, is revolved around the x-axis is
| (A) | 2π(e4 – e2) |
| (B) |  |
| (C) |  |
| (D) | 2π(e2 – e) |
| (E) | 2πe2 |
| (A) | 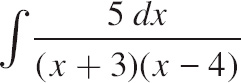 |
| (B) | 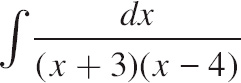 |
| (C) |  |
| (D) |  |
| (E) |  |
4. If y = 5x2 + 4x and x = ln t, then 
![]() =
=
| (A) |  |
| (B) | 10t ln t + 4t |
| (C) |  |
| (D) |  |
| (E) | 10 ln t +  |
5. 
![]() sin5 x cos x dx =
sin5 x cos x dx =
| (A) |  |
| (B) |  |
| (C) | 0 |
| (D) | −6 |
| (E) | 6 |
6. The tangent line to the curve y = x3 – 4x + 8 at the point (2, 8) has an x-intercept at
| (A) | (−1, 0) |
| (B) | (1, 0) |
| (C) | (0, −8) |
| (D) | (0, 8) |
| (E) | (8, 0) |
7. The graph in the xy-plane represented by x = 3sin(t) and y = 2cos(t) is
| (A) | a circle |
| (B) | an ellipse |
| (C) | a hyperbola |
| (D) | a parabola |
| (E) | a line |
| (A) |  |
| (B) |  |
| (C) | 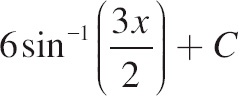 |
| (D) |  |
| (E) |  |
9. 
![]() is
is
| (A) | 0 |
| (B) | 2 |
| (C) | 4 |
| (D) | 4π |
| (E) | nonexistent |
10. The position of a particle moving along the x-axis at time t is given by x(t) = ecos(2t), 0 ≤ t ≤ π. For which of the following values of t will x′(t) = 0?
| I. | t = 0 |
| II. | t =  |
| III. | t = π |
| (A) | I only |
| (B) | II only |
| (C) | I and III only |
| (D) | I and II only |
| (E) | I, II, and III |
| (A) | −1 |
| (B) | 0 |
| (C) |  |
| (D) | 1 |
| (E) |  |
12. Use differentials to approximate the change in the volume of a cube when the side is decreased from 8 to 7.99 cm (in cm3).
| (A) | −19.2 |
| (B) | −15.36 |
| (C) | −1.92 |
| (D) | −0.01 |
| (E) | −0.0001 |
13. The radius of convergence of 
![]() is
is
| (A) | (a – 2) ≤ x ≤ (a + 2) |
| (B) | (a – 2) < x < (a + 2) |
| (C) | x < –a – 2 OR x > a – 2 |
| (D) | (a – 2) > x > (–a – 2) |
| (E) | (a – 2) ≤ x ≤ (–a – 2) |
14. 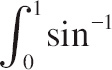
![]() (x) dx=
(x) dx=
| (A) | 0 |
| (B) |  |
| (C) |  |
| (D) |  |
| (E) |  |
15. The equation of the line normal to y = 
 at x = 2 is
at x = 2 is
| (A) | 81x – 60y = 142 |
| (B) | 81x + 60y = 182 |
| (C) | 20x + 27y = 49 |
| (D) | 20x + 27y = 31 |
| (E) | 81x – 60y = 182 |
16. If c satisfies the conclusion of the Mean Value Theorem for derivatives for f(x) = 2sinx on the interval [0, π], then c could be
| (A) | 0 |
| (B) |  |
| (C) |  |
| (D) | π |
| (E) | There is no value of c on [0, π] |
17. The average value of f(x) = x ln x on the interval [1, e] is
| (A) |  |
| (B) |  |
| (C) |  |
| (D) |  |
| (E) |  |
18. A 17-foot ladder is sliding down a wall at a rate of −5 feet/sec. When the top of the ladder is 8 feet from the ground, how fast is the foot of the ladder sliding away from the wall (in feet/sec)?
| (A) |  |
| (B) |  |
| (C) |  |
| (D) | −16 |
| (E) |  |
19. If 
![]() = 3ycos x, and y = 8 when x = 0, then y =
= 3ycos x, and y = 8 when x = 0, then y =
| (A) | 8e3sin x |
| (B) | 8e3cos x |
| (C) | 8e3sin x + 3 |
| (D) |  |
| (E) |  |
20. The length of the curve determined by x = 3t and y = 2t2 from t = 0 to t = 9 is
| (A) |  |
| (B) |  |
| (C) | 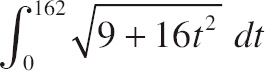 |
| (D) | 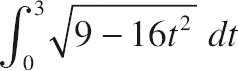 |
| (E) |  |
21. If a particle moves in the xy-plane so that at time t > 0 its position vector is (et2, e−t3), then its velocity vector at time t = 3 is
| (A) | (ln 6, ln(−27)) |
| (B) | (ln 9, ln(−27)) |
| (C) | (e9, e−27) |
| (D) | (6e9, −27e−27) |
| (E) | (9e9, −27e−27) |
22. The graph of f(x) = 
![]() has a point of inflection at
has a point of inflection at
| (A) | (0,  |
| (B) | ( |
| (C) | (0,  |
| (D) | 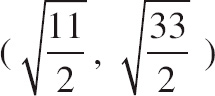 |
| (E) | There is no point of inflection. |
23. What is the volume of the solid generated by rotating about the y-axis the region enclosed by y = sin x and the x-axis, from x = 0 to x = π?
| (A) | π2 |
| (B) | 2π2 |
| (C) | 4π2 |
| (D) | 2 |
| (E) | 4 |
| (A) | 1 |
| (B) | 0 |
| (C) | −1 |
| (D) | 2 |
| (E) | Undefined |
25. A rectangle is to be inscribed between the parabola y = 4 – x2 and the x-axis, with its base on the x-axis. A value of x that maximizes the area of the rectangle is
| (A) | 0 |
| (B) | 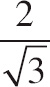 |
| (C) |  |
| (D) |  |
| (E) | 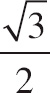 |
| (A) | sin−1 3x + C |
| (B) |  |
| (C) |  |
| (D) | sin−1  |
| (E) | 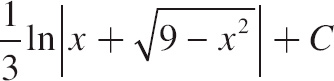 |
27. Find 
![]() .
.
| (A) | 0 |
| (B) | 1 |
| (C) | ∞ |
| (D) | −1 |
| (E) | – ∞ |
28. What is the sum of the Maclaurin series 
![]() … ?
… ?
| (A) | 1 |
| (B) | 0 |
| (C) | −1 |
| (D) | e |
| (E) | There is no sum. |
END OF PART A, SECTION I
IF YOU FINISH BEFORE TIME IS CALLED, YOU MAY CHECK YOUR WORK ON PART A ONLY.
DO NOT GO ON TO PART B UNTIL YOU ARE TOLD TO DO SO.
SECTION I, Part B
Time—50 Minutes
Number of questions—17
A GRAPHING CALCULATOR IS REQUIRED FOR SOME QUESTIONS ON THIS PART OF THE EXAMINATION
Directions: Solve each of the following problems, using the available space for scratchwork. After examining the form of the choices, decide which is the best of the choices given and fill in the corresponding oval on the answer sheet. No credit will be given for anything written in the test book. Do not spend too much time on any one problem.
In this test:
1. The exact numerical value of the correct answer does not always appear among the choices given. When this happens, select from among the choices the number that best approximates the exact numerical value.
2. Unless otherwise specified, the domain of a function f is assumed to be the set of all real numbers x for which f(x) is a real number.
29. The first three non-zero terms in the Taylor series about x = 0 for f(x) = cos x
| (A) |  |
| (B) | 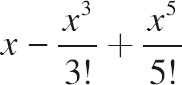 |
| (C) |  |
| (D) |  |
| (E) |  |
| (A) |  |
| (B) |  |
| (C) | sin x −  |
| (D) | sin x +  |
| (E) | sin3 x + C |
31. If f(x) = (3x)(3x), then f′(x) =
| (A) | (3x)(3x)(3ln(3x) + 3) |
| (B) | (3x)(3x)(3ln(3x) + 3x) |
| (C) | (9x)(3x)(ln(3x) + 1) |
| (D) | (3x)(3x – 1)(3x) |
| (E) | (3x)(3x – 1)(9x) |
32. To what limit does the sequence Sn = 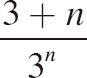
![]() converge as n approaches infinity?
converge as n approaches infinity?
| (A) | 1 |
| (B) |  |
| (C) | 0 |
| (D) | ∞ |
| (E) | 3 |
| (A) | 8ln|2x – 3| + 7ln|x + 1| + C |
| (B) | 2ln|2x – 3| + 7ln|x + 1| + C |
| (C) | 4ln|2x – 3| + 7ln|x + 1| + C |
| (D) | 7ln|2x – 3| + 2ln|x + 1| + C |
| (E) |  |
34. A particle moves along a path described by x = cos3t and y = sin3t. The distance that the particle travels along the path from t = 0 to t = 
![]() is
is
| (A) | 0.75 |
| (B) | 1.50 |
| (C) | 0 |
| (D) | −3.50 |
| (E) | −0.75 |
35. The sale price of an item is 800 – 35x dollars and the total manufacturing cost is 2x3 – 140x2 + 2,600x + 10,000 dollars, where x is the number of items. What number of items should be manufactured in order to optimize the manufacturer’s total profit?
| (A) | 35 |
| (B) | 25 |
| (C) | 10 |
| (D) | 15 |
| (E) | 20 |
36. The area enclosed by the polar equation r = 4 + cos θ, for 0 ≤ θ ≤ 2π, is
| (A) | 0 |
| (B) | 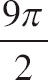 |
| (C) | 18π |
| (D) | 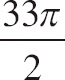 |
| (E) |  |
37. Use the trapezoid rule with n = 4 to approximate the area between the curve y = x3 – x2 and the x-axis from x = 3 to x = 4.
| (A) | 35.266 |
| (B) | 27.766 |
| (C) | 63.031 |
| (D) | 31.516 |
| (E) | 25.125 |
38. If f(x) = 
 , then
, then 
![]() is
is
| (A) | −2 |
| (B) | −1 |
| (C) | 0 |
| (D) | 1 |
| (E) | 2 |
39. The volume of the solid that results when the area between the graph of y = x2 + 2 and the graph of y = 10 – x2 from x = 0 to x = 2 is rotated around the x-axis is
| (A) |  |
| (B) |  |
| (C) |  |
| (D) |  |
| (E) |  |
| (A) | ln 3 |
| (B) | ln 4 |
| (C) | –ln 2 |
| (D) | –ln 4 |
| (E) | Undefined |
41. The rate that an object cools is directly proportional to the difference between its temperature (in Kelvins) at that time and the surrounding temperature (in Kelvins). If an object is initially at 35 K, and the surrounding temperature remains constant at 10 K, it takes 5 minutes for the object to cool to 25 K. How long will it take for the object to cool to 20 K?
| (A) | 6.66 minutes |
| (B) | 7.50 minutes |
| (C) | 7.52 minutes |
| (D) | 8.97 minutes |
| (E) | 10.00 minutes |
42. 
![]() cos x dx =
cos x dx =
| (A) | 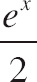 |
| (B) | 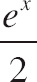 |
| (C) | 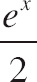 |
| (D) | 2ex(sin x + cos x) + C |
| (E) | ex(sin x + cos x) + C |
43. Two particles leave the origin at the same time and move along the y-axis with their respective positions determined by the functions y1 = cos 2t and y2 = 4sin t for 0 < t < 6. For how many values of t do the particles have the same acceleration?
| (A) | 0 |
| (B) | 1 |
| (C) | 2 |
| (D) | 3 |
| (E) | 4 |
44. The minimum value of the function y = x3 – 7x + 11, x ≥ 0 is approximately
| (A) | 18.128 |
| (B) | 9.283 |
| (C) | 6.698 |
| (D) | 5.513 |
| (E) | 3.872 |
45. Use Euler’s Method with h = 0.2 to estimate y(1), if y′ = y and y(0) = 1.
| (A) | 1.200 |
| (B) | 2.075 |
| (C) | 2.488 |
| (D) | 4.838 |
| (E) | 9.677 |
STOP
END OF PART B, SECTION I
IF YOU FINISH BEFORE TIME IS CALLED, YOU MAY CHECK YOUR WORK ON PART B ONLY.
DO NOT GO ON TO SECTION II UNTIL YOU ARE TOLD TO DO SO.
SECTION II
GENERAL INSTRUCTIONS
You may wish to look over the problems before starting to work on them, since it is not expected that everyone will be able to complete all parts of all problems. All problems are given equal weight, but the parts of a particular problem are not necessarily given equal weight.
A GRAPHING CALCULATOR IS REQUIRED FOR SOME PROBLEMS OR PARTS OF PROBLEMS ON THIS SECTION OF THE EXAMINATION.
SECTION II, PART A
Time—30 minutes
Number of problems—2
A graphing calculator is required for some problems or parts of problems.
During the timed portion for Part A, you may work only on the problems in Part A.
On Part A, you are permitted to use your calculator to solve an equation, find the derivative of a function at a point, or calculate the value of a definite integral. However, you must clearly indicate the setup of your problem, namely the equation, function, or integral you are using. If you use other built-in features or programs, you must show the mathematical steps necessary to produce your results.
1. Let f be the function given by f(x) = 2x4 – 4x2 + 1.
| (a) | Find an equation of the line tangent to the graph at (−2, 17). Verify your answer. |
| (b) | Find the x- and y-coordinates of the relative maxima and relative minima. |
| (c) | Find the x-coordinates of the points of inflection. Verify your answer. |
2. Water is draining at the rate of 48π ft3/sec from the vertex at the bottom of a conical tank whose diameter at its base is 40 feet and whose height is 60 feet.
| (a) | Find an expression for the volume of water (in ft3) in the tank in terms of its radius at the surface of the water. |
| (b) | At what rate (in ft/sec) is the radius of the water in the tank shrinking when the radius is 16 feet? |
| (c) | How fast (in ft/sec) is the height of the water in the tank dropping at the instant that the radius is 16 feet? |
SECTION II, PART B
Time—1 hour
Number of problems—4
No calculator is allowed for these problems.
During the timed portion for Part B, you may continue to work on the problems in Part A without the use of any calculator.
3. Two particles travel in the xy-plane. For time t ≥ 0, the position of particle A is given by x = t + 1 and y = (t + 1)2 – 2t – 2, and the position of particle B is given by x = 4t – 2 and y = −2t + 2.
| (a) | Find the velocity vector for each particle at time t = 2. |
| (b) | Set up an integral expression for the distance traveled by particle A from time t = 1 to t = 3. Do not evaluate the integral. |
| (c) | At what time do the two particles collide? Justify your answer. |
| (d) | Sketch the path of both particles from time t = 0 to t = 4. Indicate the direction of each particle along its path. |
4. Let f be the function given by f(x) = e−4x2.
| (a) | Find the first four non-zero terms and the general term of the power series for f(x) about x = 0. |
| (b) | Find the interval of convergence of the power series for f(x) about x = 0. Show the analysis that leads to your conclusion. |
| (c) | Use term-by-term differentiation to show that f′(x) = −8xe−4x2. |
5. Let R be the region enclosed by the graphs of y = 2ln x and y = 
![]() , and the lines x = 2 and x = 8.
, and the lines x = 2 and x = 8.
| (a) | Find the area of R. |
| (b) | Set up, but do not integrate, an integral expression, in terms of a single variable, for the volume of the solid generated when R is revolved about the x-axis. |
| (c) | Set up, but do not integrate, an integral expression, in terms of a single variable, for the volume of the solid generated when R is revolved about the line x = −1. |
6. Let f and g be functions that are differentiable throughout their domains and that have the following properties:
| (i) | f(x + y) = f(x)g(y) + g(x)f(y) |
| (ii) |  |
| (iii) |  |
| (iv) | f′(0) = 1 |
| (a) | Use L’Hôpital’s Rule to show that 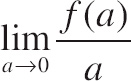 |
| (b) | Use the definition of the derivative to show that f′(x) = g(x). |
| (c) | Find  |
STOP
END OF EXAM