I. ANALYSIS AND SYNTHESIS: MATHEMATICAL METHOD AND DISCIPLINE

MATHEMATICAL COMMENTARY

1. The double classification of analysis and synthesis

Preliminary propositions

The first chapter of the treatise is devoted, in its entirety, to illustrating the classification of the different kinds of analysis that was set up in the introduction, and the classification of the forms they take in the mathematical sciences: arithmetic, geometry, astronomy and music. The intention is obviously as much logical and methodological as it is didactic; so we shall not encounter any new mathematical research in this chapter. But, before setting out on this work, Ibn al-Haytham first states three propositions relevant to analyse as a whole, both theoretical and practical. These propositions, all of which are taken from his book The Knowns, again ensure continuity with that work. So it is likely that they tell us something about the direction in which the mathematician’s thoughts were turning. It is no surprise that they are all concerned with geometrical transformations. Let us look at them one by one.

Proposition 1. — Given two fixed points A and B and two segments G and E, to show that the point C defined by the relation 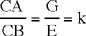lies on a circle whose centre and radius are known.

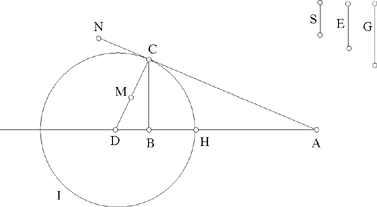
Fig. 2.1

We assume k > 1. If C satisfies the conditions, we have CA > CB. Let us extend AB and construct the straight half line CM such that AĈM = CB̂X; since CB̂X > BĈA, the straight half line CM lies outside AĈB. We have AĈM + CÂB < 2 right angles; so CM cuts AB at the point D beyond B.

The triangles ACD and BCD have a common angle D and AĈD = CB̂D; so they are similar, hence

so

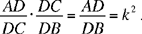
From which it follows that

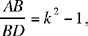
so

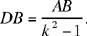
So the point D is determinate, and

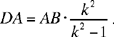
Moreover,

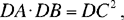
hence

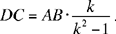
That is, the point C lies on the circle with centre D and radius k .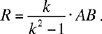

First we may note that this same problem, with its converse, appears in The Knowns, Proposition I.9. The converse also appears here in Problem 20.

Next we may note that, for the time being, Ibn al-Haytham has only carried out the analysis: if C satisfies 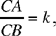then C lies on the circle with centre D and radius 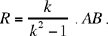The converse: any point C of the circle (D, R) satisfies 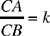will be dealt with later, as we said.

This converse shows that the points H and H’, the points of intersection of the circle and the straight line AB, divide the segment AB in the ratio k; so (A, B, H, H’) is a harmonic range.

We may note that, in a different form, this problem was studied by Ibn Sinān.¹ In the statement of the problem Ibn Sinān assumes a priori that the locus of the points is a circle. He describes Apollonius’ analysis, as well as a synthesis by his own grandfather Thābit ibn Qurra.² As it is presented, Ibn al-Haytham’s analysis seems to be a more solid version of that of Apollonius.

Proposition 2. — Given a fixed circle with centre E and radius R, and a fixed point C, if with any point A of the circle we associate the point D on CA produced such that 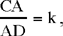then D lies on a circle whose centre and radius are known.

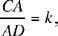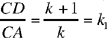Let A be an arbitrary point on the circle (E, R) and D the point on CA produced such that then is known.

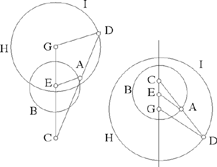
Fig. 2.2

Let G be a point on CE such that DG ║ EA, and the triangles CEA and CGD are homothetic, so 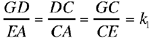so CG = k₁CE and GD = k₁EA = k₁R. The point D lies on the circle with centre G and radius k₁R, that is the circle homothetic with the given circle in the homothety .

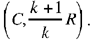Here Ibn al-Haytham does not investigate the converse: any point D lying on the circle 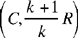satisfies 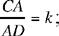whereas the problem, with the converse, appears in The Knowns, Proposition I.3.

Proposition 3. — Given a fixed point C and a fixed straight line AB, C ∉ AB and D is an arbitrary point on the straight line AB; the point E defined by CD̂E = α (a given angle) and 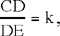a given ratio, lies on a fixed straight line.

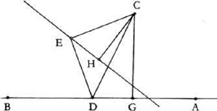
Fig. 2.3

Let E be a point that fulfills the conditions for the problem; the triangle CDE has a known shape, that is it is similar to a known triangle; so GĈH ˆ DĈE = β, a known angle, and 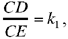a known ratio. We draw CG perpendicular to AB, and we construct the point H such that ĜCH = ˆ DCE = β and

(1)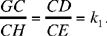

We have

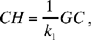
so H is a known point.

From (1) we obtain

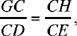
thus the triangles CHE and GCD are similar, and consequently angle CHE is a right angle. So the point E lies on the straight line Δ which is the perpendicular to the straight line CH at H.

We may note that in the similarity with centre C, with angle β and ratio 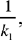the point G has image H, because 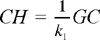and ĜCH = β. The given straight line AB, perpendicular to CG at G, has as its image the straight line Δ, perpendicular to CH at H, and any point D of AB has as its image a point E lying on Δ.

Thus, the analysis has led Ibn al-Haytham to give an account of the properties of a similarity. He considers the same problem, and its converse, in his treatise The Knowns, Proposition I.4.

We have just seen that at the start of his first chapter Ibn al-Haytham presents three propositions to which he will return in his treatise The Knowns, and that he presents them as having a bearing on analysis as a whole. Looking at the matter more closely, we may in fact observe that they have some common characteristics. All three are of the following form: if the position of a point is defined by means of known elements and has a property P, then the point lies on a known line L, a circle or a straight line. However, in the first proposition this line or straight line is obtained as a locus of points, whereas in the following two propositions it is the result of a transformation of a figure by a similarity. In the first proposition, in fact, we prove that the set of points C such that 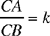is a circle whose centre lies on AB; the endpoints of the diameter are harmonic conjugates of A and B in the same ratio k. This circle, associated with the harmonic range, will reappear in Problem 20 and in the last two transformations – a homo-thety and a similarity – that Ibn al-Haytham uses in Problem 21. So the motivation behind the first proposition is clear, and is connected with the introduction of these transformations. It is, moreover, specifically these two that are treated in Propositions 2 and 3. These first three propositions serve as an introduction for all the others, and stand apart from them as providing methods that will be employed later on. They give an early indication of what The Knowns have also told us, namely that geometrical transformations played an important part in Ibn al-Haytham’s reflections on analysis and synthesis.

Analysis and synthesis in arithmetic

1. The theoretical section of the arithmetical problems

1.1. Synthesis as the converse of analysis

Proposition 4. — Let 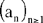be a sequence of positive integers; if

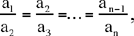
then

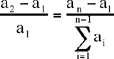
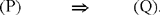
Analysis: With the help of Elements VII.11 and 12, Ibn al-Haytham proves that

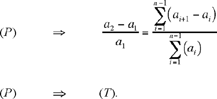
For (P) ⇒ (Q) to be true, it is necessary that

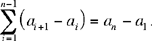
Ibn al-Haytham proves that this equation holds (moreover, it holds whether or not the integers are proportional).

Synthesis: We know, as we have seen in the course of the analysis, that

(1)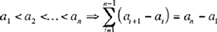

and that

(2)       (P) ⇒ (T)

from (1) and (2) we obtain (P) ⇒(Q).

Accordingly the condition is necessary and sufficient, and the synthesis is indeed the converse of the analysis. The only difference between analysis and synthesis is the order in which the premises are arranged; the synthesis is derived from implication being transitive.

1.2. Analysis leading to an impossibility: reductio ad absurdum

The preceding analysis led to a condition that was satisfied by what was given. This time we have an analysis that ends in an impossibility. The analysis is itself a proof if it is taken as a demonstration by reductio ad absurdum.

Proposition 5. — If 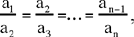then 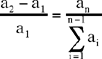is impossible.

From the preceding proposition, if

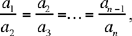
then

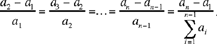
It requires that a_n = a_n – a₁, which is impossible since a₁ ≠ 0.

2. The practical section of the arithmetical problems

2.1. Practical section with discussion: synthesis as the converse of analysis

Proposition 6. — To divide two given numbers according to two given ratios.

(1)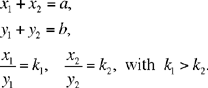

The first equation can be rewritten as

and the hypothesis k₁ > k₂ implies k₂b < a < k₁b, or again

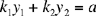
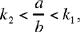
a necessary condition for the system of equations in (1) to allow of a solution. We have

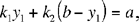
hence

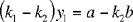
and

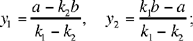
from which we find x₁ and x₂.

So if condition (2) is satisfied, the four numbers x₁, x₂, y₁, y₂ are positive and rational and give a unique solution. As this condition is possible, that is it is a condition that does not lead to a contradiction, the analysis can have a converse and its converse is the synthesis.

2.2. Analysis leading to an impossibility: reductio ad absurdum

Here Ibn al-Haytham proves that, if condition (2) is not satisfied, then the analysis results in an impossibility, and in this case it can be regarded as a proof by reductio ad absurdum.

2.3. Practical section, without discussion, problems with a unique solution: synthesis as the converse of analysis

Proposition 7. — Given an arbitrary number AB, to partition this number into two parts AC and CB where AC < CB, then into two other parts AD and DB where AD > DB, such that CB = 2 DB and AD = 3 AC.

Fig. 2.4

This problem can be rewritten as a set of four first-degree equations in four unknowns. Let the given number be n; n is positive and rational:

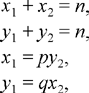
where p, q are integers, p > 1, q > 1. We have a solution

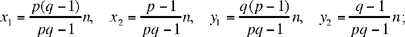
for given n, p and q, the values of x₁, x₂, y₁, y₂ can be integers or fractions, but in any case the solution is unique.

Here analysis always leads to a rational solution, without requiring conditions or discussion. Moreover, as Ibn al-Haytham writes: ‘If we invert this analysis, that allows us to complete the procedure and we establish the proof that this proposition is true.’³

2.4 Practical section, without discussion, when there is an infinite number of solutions

Proposition 8. — To find two square numbers whose sum is a square.

The solution corresponds to a modified statement: given an arbitrary square number, to find another square number such that the sum of the two is a square number. This problem has an infinite number of solutions.

So let the problem be to find positive rational numbers that satisfy

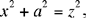where a is a given positive rational number.

It is necessary that z > x; we put

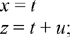
we have

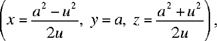
a solution that depends on a parameter u.

So in this case analysis gives us an algorithm that Ibn al-Haytham summarises as follows:

The analysis has arrived at supposing [we have] a square, an arbitrary square [a²], from which we then cut off a square [u²], an arbitrary square, subject to the condition that it is smaller than the first [a² > u²]; then we divide the remainder [a² – u²] into two equal parts 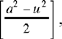next we divide the half by the side of the square that was removed 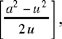we multiply the result of the division by itself 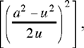then we add the result of the product to the first square 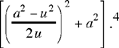.⁴

Here too the synthesis is the converse of the analysis.

Under the expression ‘practical analysis with discussion or without discussion’ (p. 225), Ibn al-Haytham silently brings together the two branches of algebra: determinate analysis and indeterminate analysis. In fact, in his work determinate analysis is represented by the practical section without a discussion with a unique solution and indeterminate analysis by the practical section without discussion with an infinity of solutions.

Analysis and synthesis in geometry

1. Theoretical section on geometrical problems

1.1. The multiplicity of analysis and auxiliary constructions

The example Ibn al-Haytham takes here is the famous proposition that is Elements I.20.

Proposition 9. — The sum of any two sides of a triangle is greater than the third side.

Ibn al-Haytham gives two of the various possible analyses for this inequality in a triangle, in each case with the required auxiliary construction. He emphasises that it is possible to give several analyses different from the two he has presented here.

1.2 Analysis that leads to an impossibility: reductio ad absurdum

Proposition 10. — The sum of any two sides of a triangle is equal to the remaining side.

2. Practical section on geometrical problems

2.1. Practical section with discussion

Proposition 11. — To divide a given segment AB into two segments that enclose a rectangle of given area C.

Fig. 2.5

This problem is that of constructing a focus of an ellipse — Apollonius, Conics III.45. Indeed Apollonius uses it several times in Cutting off a Ratio. The same problem had been considered in a similar way by Ibn Sinān.⁵

Analysis: Take a point D on AB such that AD • DB = C. If AD = DB, then

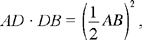
hence

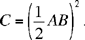
If AD ≠ DB, then

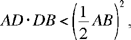
hence

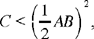
because if D exists it necessarily follows that

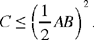
If 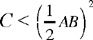and E is the mid point of AB, then C < EB². Let us put EB² — C = G, so G is known. We have

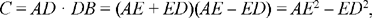
so G = ED². Consequently, ED is known and the point D is also known.

Synthesis: If 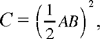D is the mid point of AB; we then have

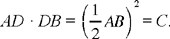
If 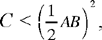, and E is the mid point of AB, we put EB² — C = G = DE², hence we have DE, and in consequence D. We then have

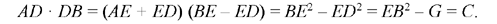
If 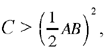the problem is impossible. Ibn al-Haytham proves this by reductio ad absurdum.

This appears a supplementary result since it has been proved that the condition 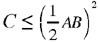is necessary.

We may note that this problem is the same as that of finding two numbers x and y when we know their sum and their product. In Propositions VI.27 and 28 of Euclid’s Elements, it appears in the form of an application of areas with a defect (ἔλλειψις).

Proposition 12. — From a given point A to draw a perpendicular to a given straight line BC, where A does not lie on BC (Fig. II.1.18, p. 257).

This problem is the same as Elements I.12. Moreover, it belongs in the following section – containing practical geometrical problems, without discussion and with a single solution. It should have appeared after Problem 13. Problems 12 and 13 are, moreover, the two cases for the problem: from a point A to draw the perpendicular to a given straight line BC, A ∉ BC (Problem 12), A ∈ BC (Problem 13).

The reversal of the order of these two problems must be the result of an accident to the text that occurred some time ago, since it is reproduced in all the manuscripts.

2.2. Practical section on geometrical problems without discussion and with a single solution

Proposition 13. — From a given point A to draw a straight line perpendicular to a given straight line BC, when the point A lies on BC (Fig. II.1.20 of the text, p. 258).

2.3. Practical section on geometrical problems without discussion having an infinite number of solutions

Proposition 14. — To construct a circle tangent to a given straight line CD and to a given circle AB, where the straight line lies outside the circle.

Ibn al-Haytham considers only the case in which the two circles touch on the outside.⁶

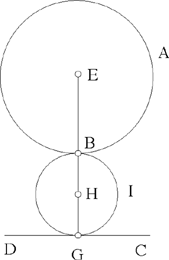
Fig. 2.6

Let E be the centre of the given circle, R its radius, H the centre of the required circle, G its point of contact with the straight line and B the point of contact of the two circles.

From Elements III.12, the points E, B, H are collinear, and HG ⊥ CD.

Analysis: 1) Let us suppose that E, H, G are collinear. Then EG ⊥ CD, so G is known; EG cuts the given circle in B, and H is the mid point of BG. Hence the synthesis for this case:

Synthesis: From E we drop a perpendicular to CD, let it be EG; it cuts the circle in B. Let H be the mid point of BG; the circle (H, HB) is a solution to the problem, it touches the straight line in G and the circle in B.

Analysis: 2) Let us suppose E, H, G are not collinear; we have HG = HB < HE. We extend HG by a length GK = BE = R; we have HK = HE= HB + R. If G is known, K is known, and the equality HK = HE implies HK̂E = KÊH; we can construct the straight line EH that cuts KG

in H.

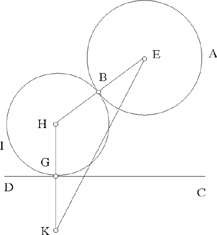
Fig. 2.7

Synthesis: Given any point G on the straight line CD, we construct GK ⊥ CD such that GK = R; given K and E on either side of CD, the angle HKE is acute; we construct K̂EH = ĤKE. We have HK = HE and BE = GK = R, hence HB = HG. The circle with centre H and radius HB touches the circle (E, EB) because H, B, E are collinear, and touches the straight line CD because HG ⊥ CD.

Thus, with every point G of the straight line CD there is associated a circle that touches both the given straight line and the given circle. So the problem admits of an infinite number of solutions.

Notes:

1) With each point G ∈ CD there is associated a point K lying on a straight line D ║ CD at a distance R. The point H, the centre of the required circle, is equidistant from the point E and the straight line D; the point H lies on the parabola P, with focus E and directrix D. Every point of the parabola P provides a solution to the problem.

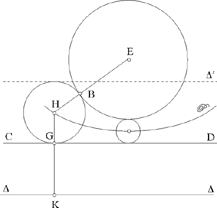
Fig. 2.8

2) If CD is a segment, a ‘straight line with endpoints’ in ancient geometry, the set of points H is an arc of a parabola.

3) If we consider the straight line Δ’, symmetrical to Δ with respect to DC, any point of the parabola P’ with focus E and directrix Δ’ is the centre of a circle that touches CD and the circle E; the circles thus touch one another internally (HK = HE = HB – R).

Finally we may note that, in the course of all his explanations about analysis and synthesis in geometry, Ibn al-Haytham has avoided raising the question of whether one can construct a converse.

Analysis and synthesis in astronomy

This is the same as in geometry and in arithmetic because Ibn al-Haytham writes:

As for problems that refer to astronomy, most of them reduce to numerical problems or to geometrical problems; their examples are the examples we gave earlier.⁷

But, among these problems, we can identify a particular group, problems ‘that refer to explanations of the motions of the heavenly bodies’.⁸ In this particular group that relates to celestial kinematics, Ibn al-Haytham illustrates analysis by considering the example of the motion of the Sun.

The problem is an old one. The ancients showed that the angles with their vertex at the centre of the instrument, the angles swept out in equal times by the radius joining this centre to the centre of the Sun, are unequal. Now, for these astronomers, the motion of the Sun must be regular, that is circular and uniform, hence the conclusion that the observed motion, that is the apparent motion, is different from the real motion, and that this effect results from the position of the orb of the Sun.

Now, the shape of the Universe is a sphere, and the centre of the Sun moves in a plane that cuts the celestial sphere in a great circle. The motion of the Sun with respect to this circle is ‘different’, that is, it is not a uniform circular motion. From this departure from uniformity, the ancients determined the position of the orb of the Sun, in the plane of the great circle, an orb that then described a regular motion.

Let E be the centre of the Universe, (ABCD) the great circle in which the plane cuts the Universe; the orb of the Sun being a circle in this plane, its centre lies in this plane; let G be this centre and (HIMN) the circle, the centre of the Sun describes the circle (HIMN) in a regular motion.

If the points G and E were identical, the arcs traversed on the two circles in the same time would be similar, which is impossible because the motion on the circle (HIMN) is regular and that on (ABCD) is ‘different’; so G ≠E.

If the Sun is in H, it is seen in A; if it is in K, it is seen in L. It has traversed the arc HK on its orb and the arc AL on the circle G. We have HGK HĜK > AÊL, so the motion of the Sun on the circle (E) in the neighbourhood of A is slower than its motion on the orb. Let BD ⊥ AC; the arc AD is a quarter of a circle, the arc HN is greater than a quarter of a circle, the arc DC is a quarter of a circle and the arc NM is smaller than a quarter of a circle. The arcs BAD and BCD are semicircles. The arc IHN is greater than a semicircle, the arc IMN is smaller and the motion on (HIMN) is regular. So the apparent motion of the Sun on BAD is faster than that on BCD, and this is indeed what is seen.

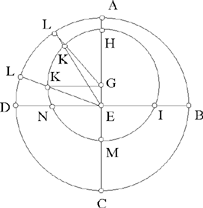
Fig. 2.9a

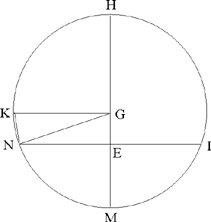
Fig. 2.9b

Let us determine the ratio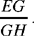

Since the motion is regular, the arcs that are traversed are proportional to the time taken to traverse them. If t₁ and t₂ are the times, in hours, that the Sun takes to traverse the arcs IHN and IMN, and if we draw GK parallel to EN, we have

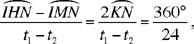
and the arc KN is thus known

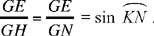
So the argument allows us to calculate the ratio 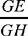but not to find the distance EG.

Thus, proceeding by analysis, Ibn al-Haytham has proved that if the Universe is a sphere with centre E, and the motion of the Sun is circular and uniform on a circle with centre G and radius GH, then 1) G ≠ E; 2) the ratio 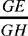is known.

Analysis in music

Here Ibn al-Haytham is still more laconic than in astronomy. He does no more than remind us that such analysis reduces to analysis of numerical problems and considers an example: the interval of an octave is composed of the interval of a fourth and the interval of a fifth.

It is clear that, as for astronomy, Ibn al-Haytham is not presenting anything very new here, but, by mentioning these two subjects, he is trying to be comprehensive. Finally, we should emphasise that an exception has been made for celestial kinematics.

2. Applications of analysis and synthesis in number theory and in geometry

The second chapter of the Treatise makes up about half the work, and comprises six examples in all, divided into two groups, three examples on number theory and three on geometry. Are arithmetic and geometry not the mathematical disciplines to which all the others can be reduced? On this point, at first glance, Ibn al-Haytham is in line with tradition. But, here as elsewhere, we must not let ourselves be deceived: though the bottles are the same, the wine is different. The terms ‘arithmetic’ and ‘geometry’ have already experienced serious changes of meaning.

Finally, we need to ask about the author’s intention in writing this work and about his choice of examples. For this it is best to look to Ibn al-Haytham’s text. And, indeed, no one could explain matters better than he does himself in presenting this second chapter in the following terms:

It remains for us to set out problems of analysis involving some difficulties, so that analysis becomes a tool to be used by anyone who works through this treatise and a guide for anyone who is trying to acquire the art of analysis; so that this analysis may be directed by the propositions that are used in it and by the complementary results that are added to its objects so that he can exercise the art of analysis.⁹

So Ibn al-Haytham’s intention seems to be transparent: to provide his readers with difficult examples, to give them practice in the art of analysis and to make them familiar with exercising it, and in particular to lead them to seek out the auxiliary constructions that are so necessary in the application of analysis: his purpose is obviously methodological and didactic. Although the term ‘methodology’ can often be misleading, what we have here is the presentation of several ‘models’ or ‘model problems’ for carrying out analysis and synthesis: six models in all, which correspond to six research situations from which the reader can draw inspiration, or, at the least, which he can use as a basis for imitation. What we mean by ‘model’ is much more than a mere illustration. The proof of this is that some of these models, as Ibn al-Haytham himself admits, refer to difficult questions. This deliberate choice shows that his intention is not purely didactic. Ibn al-Haytham chooses research problems of the time: a theorem on perfect numbers, the construction of a circle to touch three given circles, and so on. Thus, we are dealing with problems that were subjects of debate at the time, and specifically so among mathematicians in the tradition to which Ibn al-Haytham himself belonged. So everything points to his wanting to tell his reader, so to speak in vivo, how to progress, step by step, along the path of analysis, and to find the ‘complementary results’ necessary for the purpose.

But, although this reasoning helps us understand his choices, it is not sufficient to explain the area from which these items are taken, notably in geometry. For this, we need to bear in mind the ‘double’ of this treatise, namely the treatise The Knowns. As we shall see, in the course of his geometrical analysis it is precisely the properties of position and form that are, above all, of interest to Ibn al-Haytham.

So let us turn our attention to these ‘model problems’.

Number theory

Perfect numbers

Ibn al-Haytham seeks to prove the theorem about even perfect numbers that can be rewritten as follows:

Theorem. — Let n be an even number, σ₀ (n) the sum of the proper divisors of n; the following conditions are equivalents:

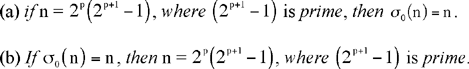
Condition (a) is none other than Proposition IX.35 of Euclid’s Elements, while condition (b) was to be given a definitive proof only by Euler. But, as far as I know, the first attempt to prove it was that by Ibn al-Haytham. In any case, he was the one who stated the condition and tried to prove it.

To understand the choice of the example of perfect numbers, we need only remember that research into the properties of these numbers had been revived by Thābit ibn Qurra,¹⁰ and that al-Khāzin had also been interested in them. ¹¹ Nearer to Ibn al-Haytham’s time, we meet al-Anṭākī,¹² and, among his contemporaries, al-Baghdākī.¹³ These mark stages in the long journey of research before Ibn al-Haytham and in his time.

Employing the analytical approach, we suppose that the number is n, and let its proper divisors also have been found, and we suppose their sum is equal to the number. So this number has divisors and these have properties: we need to find them. Because of this Ibn al-Haytham first proves

(1)

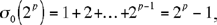
hence, when n is an even perfect number,

(2)

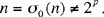
So a perfect number cannot be of the form 2^p. Ibn al-Haytham establishes this result by reductio ad absurdum:

If n = 2^p, then n — 1 = 1 + 2 + … + 2^p−1; and, from (1), we obtain n = n − 1. Thus, if a number of the form 2k has as its proper divisors each of the terms that precede it — in the same way as the perfect number — it is nevertheless not equal to their sum. On the other hand, the definition of a perfect number is that it is equal to the sum of its divisors.

We consider an even number n and a sequence D₁ of its proper divisors that forms a geometric progression with common ratio 2 that ends with n/2 : 2^p−1g, 2^p−2g, …, 2g, g where 2^pg = n. We suppose that the other divisors also form a geometric progression D₂ with common ratio 2 : 1, 2, …, 2^q–1, 2^q and that g = 2 • 2^q – 1. The two sequences of divisors, excluding 1, appear as pairs of divisors; so we have p = q, which Ibn al-Haytham also establishes by reductio ad absurdum. The sum of the divisors of D₁ is (2^p – 1) g = n — g and the sum of the divisors of D₂ is 2^q+1 – 1 = g, so the complete sum is n — g + g = n and n is perfect.

Finally, Ibn al-Haytham proves that g is prime.

Let us suppose that g is not prime; there exists d|g, d ≠1. But d|n, so d ∈ D₁ ∪ D₂. Now d < g, so d ∉D₁; and on the other hand d ≠2^k, so d ∉D₂, because the terms of D₂ are the divisors of 2^q+1 = g + 1. It follows that d = 1. So it is clear that Ibn al-Haytham is in fact only giving a partial converse of Euclid’s theorem. He does not prove that, among all even numbers, only Euclid’s are perfect; he merely proves that, among even numbers of the form 2^p(2^q+1–1), only Euclid’s are perfect.

Ibn al-Haytham then performs the synthesis. He takes a number n = 2^pg, where g is a number such that

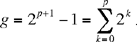
We have

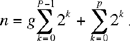
Each number in D₁ or D₂ (for p = q) is indeed a divisor of n. Let us suppose that d is a divisor of n, then there exists e, a divisor of n, such that d • e = n = 2^pg; we have

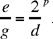
If g is a factor of e, then d is a factor of 2^p and d ∉ D₂. If g is not a factor of e, (g, e) = 1 because g is prime; accordingly e is a factor of 2^p, and e = 2k (1 ≤ k ≤ p); so d = g2^p-^k, d ∉ D₁. Any divisor of n appears in D₁ or in D₂. We conclude that n is equal to the sum of his divisors; so n is perfect.

This half-failure should not obscure the whole: we have a serious attempt to find a property that characterises all even perfect numbers. This ‘model problem’ cannot be a mere illustration of analysis and synthesis in arithmetic designed for beginners; it is a piece of ongoing research in which Ibn al-Haytham is applying this method in number theory.

In considering the theorem on perfect numbers, Ibn al-Haytham is dealing with an important example in number theory, as the subject is defined by Euclid. In the course of his analysis Ibn al-Haytham raises the problem of the existence of these numbers, of their form, of the ‘cause’ (‘illa) by which they have this form and finally the problem of their identification as a class of numbers; that is he proposes a criterion for distinguishing them as a class of numbers. Moreover, this is the reason that led him to prove the converse of Euclid’s proposition. It is precisely this research into existence and form that justifies employing the method of analysis in arithmetic, even by way of analogy. In the two following examples, Ibn al-Haytham turns back towards the other tradition in number theory in the tenth century, the tradition of rational Diophantine analysis.

Two indeterminate systems of equations of the first degree

On this occasion also, Ibn al-Haytham is not concerned merely with providing solutions to the systems in rational numbers, but rather with establishing the existence, form and number of the solutions. So in each case the analysis must lead us to express these elements as clearly as possible, as is apparent from the text. Here we shall provide only the statements of the problems.

The first system may be written as

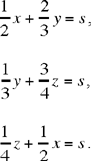
Ibn al-Haytham begins by proving that

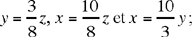
which tells him that the required numbers have known ratios one to another: so they exist and are positive rational numbers. As for their form, Ibn al-Haytham proves in his synthesis that to any integer n ≡ 0 (mod 8) there corresponds a solution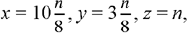

The second problem is stated as follows: if k₁, k₂, k₃ are given ratios, and a and b two given numbers, to partition a and b so that

(*)

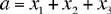
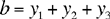
where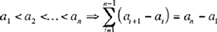

Here again Ibn al-Haytham makes a point of establishing the existence, form and number of the solutions. While employing a different style of expression, let us follow Ibn al-Haytham’s reasoning. The first equation of (*) can be rewritten

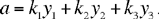
But, 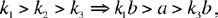hence the necessary condition

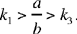
Let us put

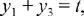
then

and

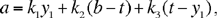
hence

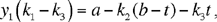
hence

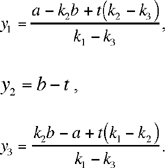
Discussion: First of all we need to know whether the conditions 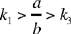and 0 < t < b are sufficient to make y₁, y₂, y₃ positive.

• If 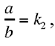the three numbers y₁, y₂, y₃ are positive for 0 < t < b,

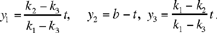
• If 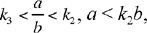we have y₂ > 0, y₃ > 0; but

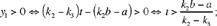
the three numbers are positive if

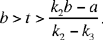
• If 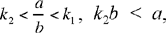we then have y₁ > 0, y₂ > 0; but y₃ 0 requires that

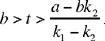
Notes:

1) In the course of his synthesis, Ibn al-Haytham distinguishes three cases:

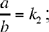• he takes as parameter BM = y₂ = b — t.

• If 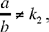Ibn al-Haytham takes as parameter 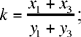we have

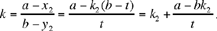
• If 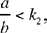we have 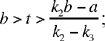from which we deduce

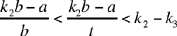
and in consequence

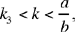
which is the condition Ibn al-Haytham imposes on the ratio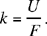

• If 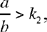we have 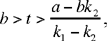hence

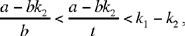
and in consequence

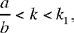
without again encountering the condition Ibn al-Haytham imposed on the ratio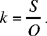

2) The method Ibn al-Haytham uses has the aim of reducing this problem to Problem 6. He accordingly takes as auxiliary unknowns 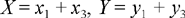and a parameter 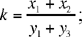so we need .

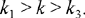The initial system can be rewritten

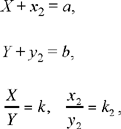
which corresponds to Problem 6.

Here the ratios 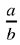and k₂ are given. From the investigation of Problem 6, if 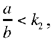we need to choose k in the interval 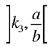in order to have 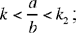and if 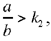we need to choose k in the interval 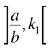in order to then find

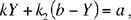
hence

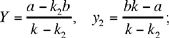
from which we deduce X and x₂.

It remains to solve the system

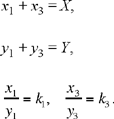
We know that 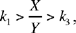from the choice of the parameter k; so this Y system has a unique solution if X and Y are taken to be known. Ibn al-Haytham is thus led to address an additional problem: to find a ratio lying between two given ratios.

Geometrical problems

Ibn al-Haytham chooses three problems, of which the first, and simplest, is a problem in plane geometry; the second deals with geometrical transformations and the third is concerned with a geometrical construction. This sequence of choices does not seem to arise purely as a matter of chance, but relates to three areas of geometry, in which there had been perceptible development.

Problem in plane geometry

The first problem is the simplest. It can be written:

Given three points A, C, B in that order, and a straight line DG, to find a point E of that straight line such that EC bisects the angle AEB.

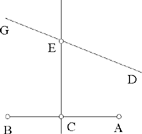
Fig. 2.10

Analysis: If EC bisects the angle AEB, we have

1) If C is the mid point of AB, we have CA = CB, hence EA = EB, and E lies on the perpendicular bisector of AB.

2) If is a known ratio; so the point E lies on a known circle, let CI be its diameter (see Problem 1). So E is both on this circle and on the straight line DG.

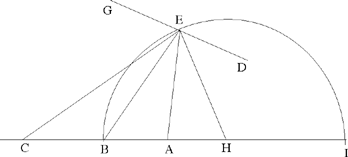
Fig. 2.11

Synthesis:

1) We draw Δ to be the perpendicular bisector of AB. If DG is not perpendicular to AB, Δ cuts DG at the point E, and we have EA = EB. The triangle EAB is isosceles, and the height EC bisects the angle at E; the problem has one solution.

If DG ⊥ AB and DG ≠ Δ, the point E does not exist. If DG = Δ, any point of DG provides a solution (Fig. 2.10).

2) Ibn al-Haytham takes CA > CB, and defines H by

(1)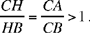

There exist two points H that satisfy the equation. Ibn al-Haytham finds the one between C and B, and the other one beyond B. He chooses the latter without giving details, perhaps because of the analogy with Problem 1 (in that problem the point D, which corresponds to the point H here, was defined by a different procedure, and lay on the extension of AB).

In any case, as the point H lies beyond B, we have

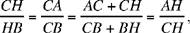
hence

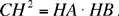
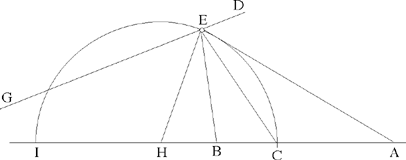
Fig. 2.12.1

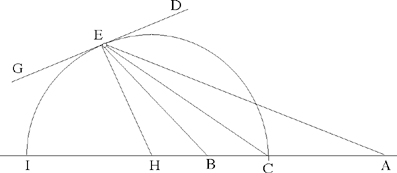
Fig. 2.12.2

Ibn al-Haytham then proves that the circle (H, HC) with diameter CI is the known circle of the analysis. Indeed if this circle cuts DG in E, we have

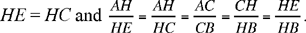
So the triangles AHE and BHE are similar, hence

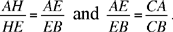
We may note that this proof for a point E of the circle (H, HC) is a proof of the converse that was not supplied in Problem 1; it establishes that any point E of the circle (C, CH) satisfies

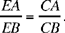
Discussion: The existence of the point E depends on the distance h from the point H to the straight line DG. Let R be the radius of the circle:

h > R	the problem has no solution
h = R	the problem has one solution
h < R	the problem has two solutions.

We may note that in this problem Ibn al-Haytham deals with the set of points E such that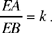

If k = 1, the set is the straight line A the perpendicular bisector of AB;

If k ≠ 1, the set is the circle with diameter CI, where C is given, and I is the harmonic conjugate of C with respect to A, B.

 

Problem solved with the help of transformations

The second problem in this group is more than merely more complicated, and in it Ibn al-Haytham proceeds by means of geometrical transformations. Its statement is:

Given a fixed point A, a circle centre G and a straight line BC, to find a point D on the circle (G) and a point H on BC such that the angle 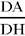is equal to a given angle and

The data for the problem show that the given point A and the required points D and H define a triangle of ‘known shape’, that is similar to a given triangle. So we can put the angle DAH = α, a known angle, and 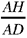a known ratio.

1) The point H can be found from D by one of the similarities:

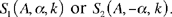
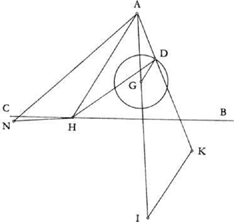
Fig. 2.13

To establish the existence of the point H is to prove that it lies at the intersection of the given straight line BC and one or other of the circles T₁ = S₁(G) or T₂ = S₂(G).

2) Similarly we can say that D is found from H by one of the similarities

So if the point D exists, it lies at the intersection of the circle G and one or other of the two straight lines

In both cases, the synthesis compels us to discuss the intersection of a straight line and a circle.

Ibn al-Haytham proposes two analyses of this problem. In the first, he begins by using a homothety with centre A in which the circle (G, GD) has as its image the circle (I, IK); then he uses a similarity with centre A, in which the circle (I, IK) has as its image the circle (N, NH). The combination of the homothety and the similarity gives one of the similarities mentioned in 1).

In his second analysis, Ibn al-Haytham proves that D lies on the straight line found from BC by one of the similarities mentioned in 2). He then gives two syntheses, which contain nothing of particular interest. For each of these two syntheses, he points out that it compels us to discuss the intersection of a straight line and a circle. This discussion also gives him the number of solutions.

 

Construction of a circle to touch three given circles

The third geometrical problem – the last in the second chapter and thus the last in the Treatise – is the most important of all, equally for the place it occupies and for its history and the challenge it posed. This last ‘model problem’ occupies about a fifth of the Treatise as a whole. On the other hand, it is the problem that had already been posed by Apollonius, one to which Pappus and many others had returned. Finally, this same problem had been an object of controversies among Ibn al-Haytham’s predecessors. So we have a problem with a noble lineage, but still open and thus a matter for ongoing research. In regard to the nature of the problem itself, historians of geometry have emphasised the profundity of the problem and the difficulty it presented at that time. J. L. Coolidge sees it as marking exactly the limit of what Greek mathematicians could do.¹⁴

The history of this problem is too well known to be worth further discussion here. Ver Eecke has already provided two accounts of it.¹⁵ Let us simply note that Apollonius poses the problem in his now-lost book The Tangencies. It is probably this book that was translated into Arabic under the title The Tangent Circles (al-Dawā’ir al-mumāssa), which the tenth-century biobibliographer al-Nadīm mentions as among the books by Apollonius known in Arabic.¹⁶ This Arabic translation has now itself been lost. The most direct testimony is still that of Pappus, who reports that this book included some propositions that ‘they seem to have been numerous, but for them too we shall take only one’. This, it seems, sets out the question raised by Apollonius:

If any three elements are given successively in position, such as points, or straight lines and circles, to describe a circle that, passing through each of the given points (in the case where points are given), or tangent to each of the given lines.¹⁷

A simple exercise in combinatorics gives the problems to be solved, which Pappus lists: 1) three points, 2) three straight lines, 3) two points and one straight line, 4) two straight lines and one point, 5) two points and a circle, 6) two circles and one point, 7) two straight lines and one circle, 8) two circles and one straight line, 9) one point, one straight line and one circle, 10) three circles.

It is the last problem that is of interest here. However, we do not know what Apollonius’ solution was, or even whether he proposed one. We are no better informed about the terms of Pappus’ solution, since that seems to have been lost in Pappus’ own time. But all this had already become a matter of legend that, as Ver Eecke writes, ‘excited the curiosity of the greatest mathematians of recent centuries’.¹⁸ Among these we should mention Viète, Descartes, Newton and, later, L. Carnot, T. Simpson, L. Euler, N. Fus, J. Lambert and Gergonne, among others. But this ‘curiosity of the greatest mathematians’ made its appearance well before the seventeenth century, since its effects can be seen in the mid ninth century and in the first half of the tenth century.¹⁹ To understand this renewed interest, we need to look at the renewal of research in geometry, notably in the area of the theory of conics and that of geometrical constructions. In the case of the present problem at least, this renewal of interest is linked with names and books that antedate Ibn al-Haytham. One figure who plays a central part is Ibn Sinān, who is also important because Ibn al-Haytham picks up on his work. Ibn Sinān, the representative of one of the great scientific dynasties of the time, the dynasty of the descendants of Thābit ibn Qurra, sheds some light on the investigations into this problem carried out in the course of the first half of the tenth century. Thus, we know, thanks to him, that a representative of another scientific dynasty – the Banū Karnīb – Abū al-‘Alā’, took an interest in this construction. A third mathematician, no negligible figure, Abū Yaḥyā, one of the teachers of the famous Abū al-Wafā’ al-Būzjānī, takes up this same problem on his own account. Ibn Sinān reports and criticises the solutions put forward by his two predecessors. He himself not only takes an interest in this problem, but also, in all probability, in Apollonius’ book The Tangencies, to the point of composing a book that has the same title as the Arabic translation of Apollonius’ work: The Tangent Circles (al-Dawā’ir al-mumāssa). In his autobiography, Ibn Sinān tells us that in this book he deals with ‘in which ways circles and straight lines are tangent to one another and pass through [particular] points, and about other things’.²⁰ This book, which has thirteen chapters, is, according to its author himself, closely connected with questions of analysis and synthesis. It has not come down to us. Ibn Sinān wrote a supplement (tatimma) to this work, a collection of forty-one problems, ‘difficult problems on circles, straight lines, triangles, tangent circles and other things, in which I have used only the method of analysis’.²¹ Ibn Sinān in fact supplies, among other things, the analysis for the problem with which we are concerned here.

It is eminently reasonable to suppose that Ibn al-Haytham knew one or the other of Ibn Sinān’s books – if not all of them. We have shown that in his research on hour lines for sundials he started from Ibn Sinān’s work, but also in opposition to him. The same is true in Analysis and Synthesis. That is to say that, together with al-Khāzin, Ibn Sahl and al-Qūhī, Ibn Sinān is one of the leading figures of the tradition that Ibn al-Haytham is trying to take forward as far as possible. So the real question is to find out why he picked up on this problem, and what differentiates his treatment of it from that of Ibn Sinān.²²

In investigating the problem of constructing a circle that touches three given circles, Ibn Sinān makes the same hypotheses as those made later by Ibn al-Haytham: the circles lie outside one another, their centres are not collinear, and the required circle touches them externally. Ibn Sinān then distinguishes three cases for the given circles C₁(K, R₁), C₂(H, R₂) and C₃(I, R₃) (see Fig. 2.14 below).

The first case is that of equal circles R₁ = R₂ = R₃.

The solution is immediate. The point L, the centre of the required circle, is the centre of the circle circumscribed about the triangle KHI, and its radius is r = LK – R₁. As we shall see, this case is ignored by Ibn al-Haytham.

The second case is that of two equal circles, R₁ = R₂.

Ibn Sinān considers the circle C(I, R₃ + R₁) if R₃ < R₁, or C(I, R₃ – R₁) if R₃ > R₁. The problem reduces to that of finding a circle that touches this circle and passes through the points K and H, a problem he has solved in his Anthology of Problems; but he provides only one solution, the second is obvious.

The third case is that in which the three circles are different from one another. Let R₃ be the smallest; Ibn Sinān reduces the problem to finding a circle that passes through the point I and touches the two circles (K, R₁ – R₃) and (H, R₂ – R₃). The solution has an error in the reasoning of the analysis, which leads Ibn Sinān to believe that a ratio is known from the data, which is not true.²³ It is this particular ratio that Ibn Sinān uses in the synthesis, in two different methods, to reduce this problem to another one that he has solved in The Tangent Circles : to construct a circle passing through a given point A and, at A, tangent to a given straight line, and tangent to a given circle.

Thus, Ibn Sinān’s analysis consists of proving that, in the three cases he considers, constructing the circle touching three given circles can be reduced to a problem that has already been solved. But we are left with the fact that the third case, that is the general case, raises the difficulty we have mentioned.

So we have a problem that Abū al-‘Alā’ ibn Karnīb and Abū Yaḥyā worked on, and one the solutions to which were criticised by Ibn Sinān; who, although an eminent and esteemed mathematician, seems himself also to have been unable to provide a solution. So there is a challenge that Ibn al-Haytham will take up. This case is, moreover, far from unique. In addition, this construction problem is connected with analysis and synthesis. So, with this background, it is not hard to understand the reasons that spurred Ibn al-Haytham into attacking this problem. He engages with it in a manner different from that of Ibn Sinān: he is interested only in the general case R₁ < R₂ < R₃. His analysis, as we shall see in some detail, is different from that of Ibn Sinān: if the required circle C(L, r) exists, then the circle C(L, r + R₁) passes through the point K, the centre of C₁, and cuts the straight lines KH and KI in two points S and O. The required point L is thus the centre of the circle circumscribed about the triangle KSO. So the analysis leads to the problem of determining the two points S and O from what is given; which led Ibn al-Haytham to an auxiliary construction for which analysis leads him to distinguish two cases, each time with a discussion.

Thus, Ibn al-Haytham’s analysis is different from that of Ibn Sinān. However, it is from the latter’s analysis that Ibn al-Haytham has started his own. In fact, his analysis brings in the circle KSO : this circle is none other than the circle to which Ibn Sinān appeals in the general case. Now it is precisely in the course of his investigation of the construction of this circle that Ibn Sinān makes the mistake in his reasoning to which we have already referred.

Thus, matters proceed as if Ibn al-Haytham has noticed this mistake and had picked up the problem starting from the same auxiliary circle as Ibn Sinān. If that is true, then we may risk advancing hypotheses: when following the steps of Ibn Sinān’s construction, Ibn al-Haytham, who had done more than anyone to develop construction methods using conic sections, does not use the differences LH – LK = R₂ – R₁ and LI – LK = R₃ – R₁ (see geometrical commentary below), which are, moreover, obvious from the figure, and which would have allowed him to construct L as the point of intersection of two branches of a hyperbola. However, in On the Completion of the Conics, Ibn al-Haytham has no hesitation in using intersections of conics, even for constructing solutions to plane problems like this one. Perhaps he wanted to follow the tradition that problems in the plane are to be solved by means of straightedge and compasses. Perhaps also, while having noticed this new possibility, he nevertheless wanted to continue along the route laid out by his predecessor, and to correct his work. Whatever we choose to believe, here as in other cases Ibn al-Haytham has conceived his construction in the terms laid down by Ibn Sinān and also against him. So let us examine Ibn al-Haytham’s solution.

Let C₁ (K, R₁), C₂ (H, R₂), C₃ (I, R₃) be three given circles, each one outside each of the others; K, H, I, which are not collinear, being their centres; R₁, R₂, R₃ the radii such that R₁ < R₂ < R₃.

Let us put HI = d₁, KI = d₂, KH = d₃, and HK̂ I = α̂ < 2 right angles.

Thus, by hypothesis d₃ > R₁ + R₂, d₂ > R₁ + R₃ and d₁ > R₂ + R₃.

To construct a circle C(L, r) touching the three circles (Fig. 2.14).

If such a circle C(L, r) exists, then the circle C(L, r + R₁) passes through K and cuts the straight lines HK and IK in S and O respectively. The aim of Ibn al-Haytham’s analysis is to prove that the points S and O are ‘known’, that is determinate from the data for the problem, and that the required point L is consequently the centre of the circle circumscribed about the triangle KSO, a known triangle.

Ibn al-Haytham supposes that L lies inside the salient angle HKI, and in this case at least one of the angles LKH and LKI is acute; hence the three cases of the figure that are considered (Figs 2.15, 2.16, 2.17).

But it is possible for L to lie outside the salient angle – in the position L₁ of Figure 2.14, and in this case at least one of the angles LKH and LKI is obtuse. Ibn al-Haytham does not consider this possibility. Moreover, he does not address the problem of the number of possible solutions.

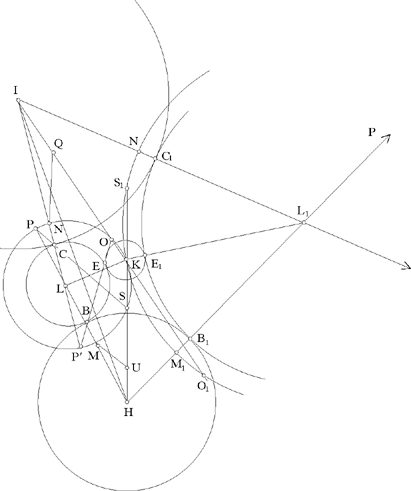
Fig. 2.14

In all cases of the figure, the circle C(L, r + R₁) cuts [HL) in M and P and [IL) in N and P’, here HM < HK < HP and IN < IK < IP’; we obtain

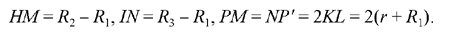
On the straight half lines [HK) and [IK), the positions of the points S and O with respect to the point K depend on the case of the figure. In the three cases investigated by Ibn al-Haytham, we have IO < IK, where HS < HK (Figs 2.14 and 2.15), HS = HK (Fig. 2.16) and HS > HK (Fig. 2.17). But in Figure 2.14, we have instead IO₁ > IK and HS₁ > HK.

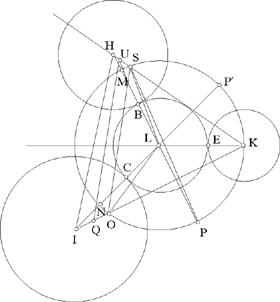
Fig. 2.15

In all the cases, we can write

hence

and

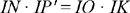
hence

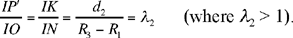
Ibn al-Haytham next defines U on [HK) and Q on [IK) by

which implies MU ∥ PS and NQ ∥ P’O, and consequently that U lies between H and S, and Q between I and O.

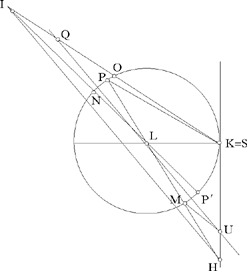
Fig. 2.16

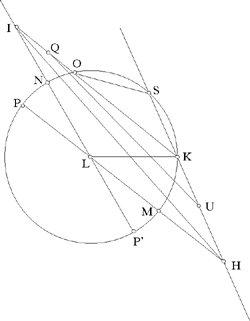
Fig. 2.17

We also have

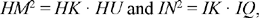
hence

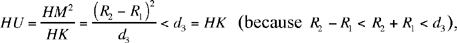
and

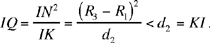
So the points U and Q are known points, U on the segment KH, Q on the segment KI and UKQ is thus a known triangle.

We have

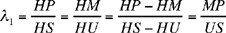
and

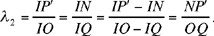
On the other hand, if K ≠ O and K ≠ S, in the triangle OKS we have OK̂S =α or OK̂S =π − α, and consequently

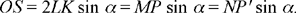
From which we deduce

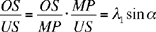
and

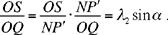
But, if K = S (Fig. 2.16), we have OS = OK = 2LK sin α, and the preceding result remains true. If K = O, the preceding result is still true.

Thus, for all cases of the figure, analysis leads to a known triangle UKQ and two points S and O on the straight half lines [UK) and [QK), defined by

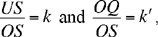
where

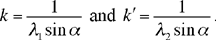
In order to establish, from these last equations, the conclusion that S and O are two known points, Ibn al-Haytham considers an auxiliary problem:

Given a triangle KUQ and two ratios k and k′, to find a pair of points (S, O), where S is on [UK) and O on [QK) such that

²⁴

The data for the auxiliary problem – the angle UKQ = α, KU, KQ, k and k’ – are all expressed in terms of those of the initial problem:

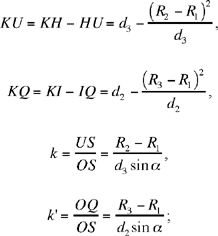
from which we obtain

In his analysis of this problem, Ibn al-Haytham distinguishes two cases:

1. 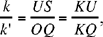    which corresponds to SO ∥ UQ;

2.    

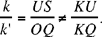
In both cases, a discussion is necessary, but it does not appear either in the analysis or in the synthesis. In fact, for the required point S to give a solution to the problem of constructing the circle with centre L, we need S to lie on the segment UK or beyond K. In case 1, there can be either one or two solutions, and in case 2, there can be no solution, or one or two solutions (see auxiliary problem).

Synthesis: Let us return to the three given circles. The circle C₁ (K, R₁) cuts HK in E and IK in G.

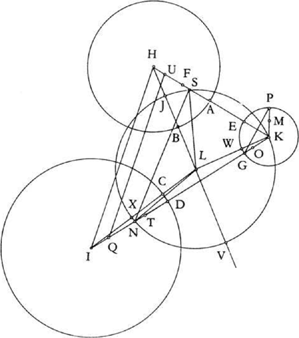
Figure 2.18

Ibn al-Haytham calls upon R₂ – R₁ = HF, where F lies on [HK ], R₃ – R₁ = IT, where T lies on [IK ], and he defines U on [HK) and Q on [IK) by HK · HU = HF₂ and IK · IQ = IT₂; these are the points U and Q of the analysis (see Fig. 2.18 above and Figs II.1.45–46, pp. 297–8).

The points S and O of the analysis here become S and N – the letters of the figures change in the synthesis.

To derive the ratios 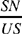et 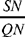in terms of the data, Ibn al-Haytham uses an auxiliary construction on the circle C₁ (K, R₁): if HK̂I = α̂, we have arc GE = α̂; we construct P such that arc GP = 2α̂, for 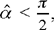, 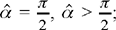; so we have GP = 2 R₁ sin α, an equality that holds in all three cases of the figure.

The points M on [PK ] and O on [KG ] are defined by

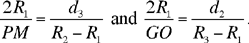
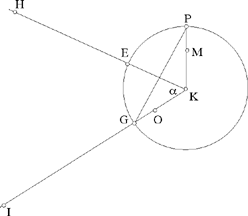
Fig. 2.19

Finally, let us put

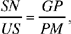
hence

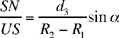
and

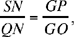
hence

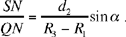
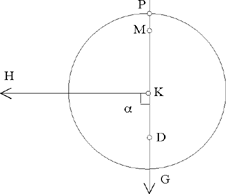
Fig. 2.20

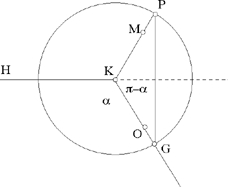
Fig. 2.21

Thus, Ibn al-Haytham has set out the expressions for the ratios investigated in his analysis, where he had merely asserted that they are known. He has obtained the points S and N. If these two points are different from K, then SKN is a triangle. To prove that L, the centre of its circumscribed circle, is the centre we require, he argues by reductio ad absurdum. In the synthesis, he does not consider the case in which one of the points S and N is identified with the point K. This possibility had, however, appeared in the second case in his analysis. If, for example, we suppose that S = K, then the point L lies at the intersection of the perpendicular bisector of [KN ] and the perpendicular to the straight line KH at K.

We may offer a brief conclusion. Ibn al-Haytham’s analysis for the three cases he investigates is correct; it is correct also for the fourth case, which he seems not to have noticed, though providing that the investigation of the auxiliary problem must itself be correct. As we shall see shortly, this last is, however, incomplete. It should have included discussions of which there is no trace in the treatise. Indeed, Ibn al-Haytham thinks that the auxiliary problem has a single unique solution in all the cases, whereas it can have two or none. We may wonder why these discussions do not appear. To look into this, we must first return to the auxiliary problem. For the synthesis, we shall merely note the auxiliary constructions that distinguish it.

Auxiliary problem

Let us put KU = b, KQ = c, UQ = a, UK̂Q = α UQ̂K = β. Let us also put US = y, OQ = z, SO = x, where x > 0, y > 0, z > 0.

Let us follow Ibn al-Haytham and distinguish the two cases of his analysis.

I)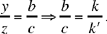

In this case, we have OS ∥ UQ, and consequently

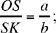
but by hypothesis

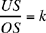
hence

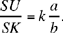
If 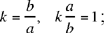one point S provides a solution to the problem, that is the mid point of [UK].

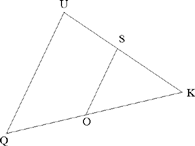
Fig. 2.22

If 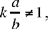, two points S on the straight line [UK) satisfy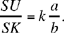

If 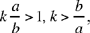, the two points provide solutions to the problem, S₁ on [UK ] and S 2 beyond K.

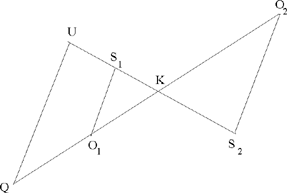
Fig. 2.23

If 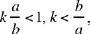the point S 1 on [UK ] provides a solution to the problem; the second point, S₂, lies beyond U, it does not lie on the straight half line [UK).

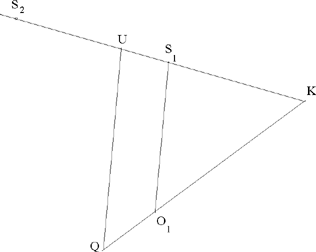
Fig. 2.24

Having found the point S, the point O is found from it, because SO ∥ UQ. Ibn al-Haytham considers only the point S₁.²⁵

II)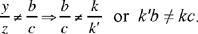

In this case, SO is not parallel to UQ. Ibn al-Haytham sets out a procedure for reducing this to the first case.

He draws through S the parallel to UQ – it cuts KQ in T; and through U he draws the parallel to SO, which cuts KQ in J. Depending on the values given for b, c, k and k’, there are several cases to be distinguished for the positions of the points K, Q, O, T and J. In fact,

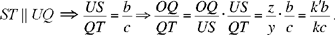
We can have

1)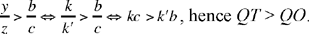

In this case, J ∈[Qz’) and JÛK =QÛK +JÛQ.

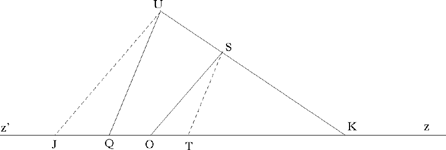
Fig. 2.25

2)      

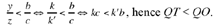
In this case, J ∈[Qz) and JÛK =QÛK +JÛQ.

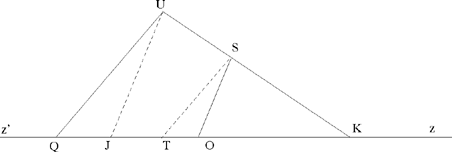
Fig. 2.26

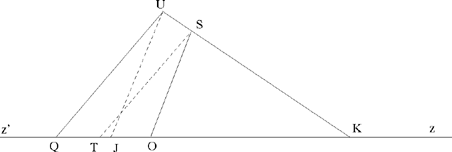
Fig. 2.27

In both cases, we have OT = | OQ – QT |, and we infer

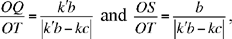, because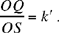

We have drawn UJ ∥ SO; because triangles UQJ and STO are similar we may write

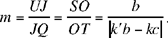
Moreover, we have UQ̂K = β, which is given. But the point J can lie on the straight half line [Qz) or on its extension. So there are two cases:

1) 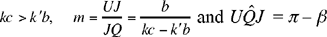      (Fig. 2.25)

2)       (Figs 2.26 and 2.27).

In both cases, the ratio 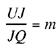and the angle UQJ are known. Ibn al-Haytham concludes from this that ‘the triangle UJQ is of known shape’. But, since the points U and Q are known, if m = 1, then J lies on Δ, the perpendicular bisector of [UQ ]; and if m ≠ 1, J lies on a circle Γ (the circle that is the locus of points M such that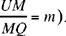

1. 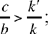; J is on the straight half line [Qz’).

If 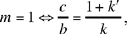Δ does not cut [Qz’) because the angle β is acute; J does not exist.

If 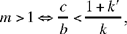the point Q lies inside Γ, Γ cuts [Qz’) in one point; J exists and is unique.

If 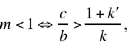U lies inside Γ and Q outside it; Γ does not cut [Qz’), J does not exist.

2. 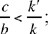J is on the straight half line [Qz).

If 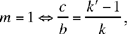Δ cuts [Qz) because β is acute. J exists and is unique.

If 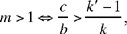Q lies inside Γ, then Γcuts [Qz) in one point; J exists and is unique.

If 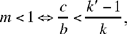the circle Γcan cut [Qz), touch it, or not cut it.

In this case, let us suppose MN is a diameter of Γ, P its centre and R its radius.

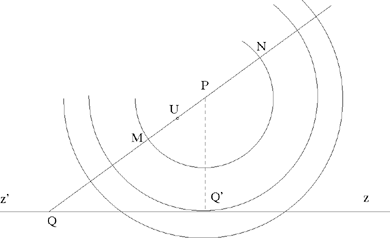
Fig. 2.28

We have

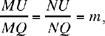
hence

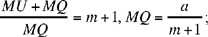
in the same way we have

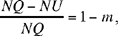
hence

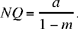
From which it follows that

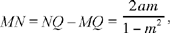
hence

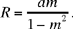
Moreover,

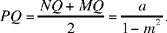
If PQ’ ⊥[Qz), we have

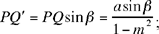
the circle will cut [Qz) in two points if PQ’ < R, that is if

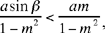
that is if m > sin β.

We have

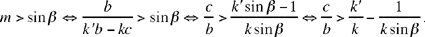
So we obtain

• if 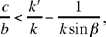the point J does not exist;

• if 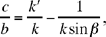there exists a unique point J on [Qz);

• if 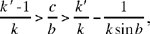there exist two points J₁ and J₂ on [Qz).

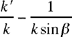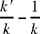Below is a summary of the complete discussion when it is assumed that β is acute, and we suppose that the two numbers and are positive.

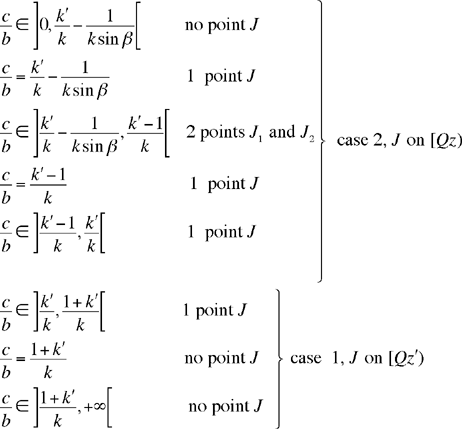
Once we have obtained the point J, the triangle KUJ is known, and we find SO as in case 1, since SO ∥ UJ. To investigate the position of O would demand a supplementary discussion when J is on [Qz’), a discussion we shall not give here.

We may also note that the method Ibn al-Haytham uses in case II assumes S ≠ K. If S = K, the parallel to SO drawn through U is parallel to QK; the point J accordingly recedes to infinity.

We have just seen that the investigation of the auxiliary problem, although correct, is not complete. Ibn al-Haytham seems to think that the problem has a unique solution in every case. But we have seen that there can be two solutions, or none.

If the conclusions we have drawn from our investigation are correct, we should ask ourselves about how this discussion came to escape Ibn al-Haytham. We can see only two lapses. The first arises from the fact that he took it that a point of a given straight line, defined by the ratio of its distances from two known points, is unique; he takes the one that lies on the segment joining the two points and neglects the one on the extension of the segment. The second lapse arises from the assertion that a triangle is defined, up to a similarity, if we are given an angle and the ratio of one side adjacent to that angle to the side that is opposite it.

It remains that Ibn al-Haytham has reduced the problem of the construction of the circle touching three given circles to the problem of the existence of the two points required in the auxiliary problem. So it is on the discussion of this latter problem that the number of solutions to the initial problem depends. Now this discussion, a very complicated one, as we have seen, was one Ibn al-Haytham did not engage upon.

 

Geometrical commentary on the problem

Let us return to the data for the problem. If the circle C(L, r) exists, we have LK = r + R₁, LH = r + R₂ and LI = r + R₃, hence

(1)        

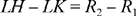
and

(2)        

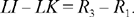
From (1) L ∈ ℋ₁, the branch around the focus K of a hyperbola whose second focus is H; and from (2) L ∈ ℋ₂, the branch around the focus K of a hyperbola whose second focus is I. So the problem of constructing the tangent circle reduces to one of the problems that Ibn al-Haytham proposed in a particular area of geometry: geometrical construction using conic sections. The whole problem is now to find out whether ℋ₁ and ℋ₂ cut one another.

If we examine the special case in which the centres of C₁, C₂, C₃, that is K, H, I, are collinear, the two branches ℋ₁ and ℋ₂ then have the same axis, and it is clear that ℋ₁ and ℋ₂ can have 0, 1 or 2 common points; consequently, the problem itself admits of 0, 1 or 2 solutions. If HK̂I= α=0, we have the following figures:

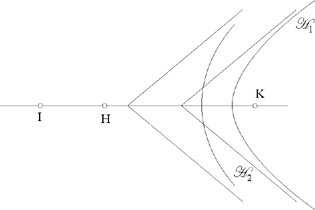
Fig. 2.29

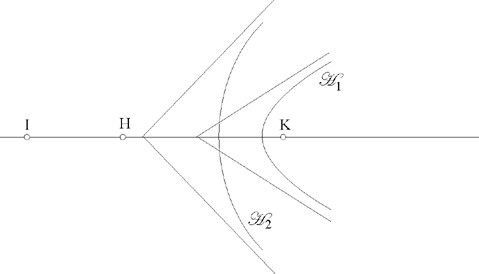
Fig. 2.30

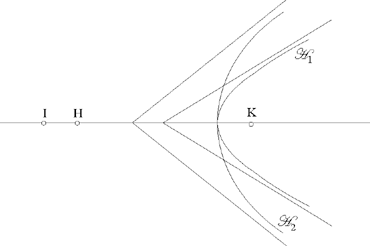
Fig. 2.31

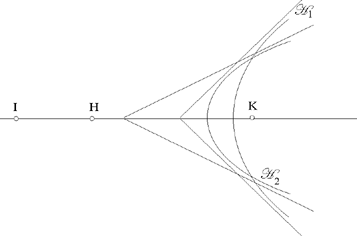
Fig. 2.32

We may note that ℋ₁ and ℋ₂ have the same vertex if and only if

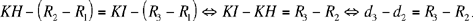
If HK̂I= α= π, ℋ₁ and ℋ₂ cut one another in two points that are symmetrical with respect to the straight line HK.

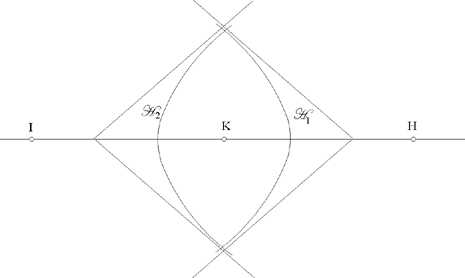
Fig. 2.33

We may also note that the asymptotes are parallel if and only if

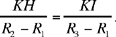
If in addition, HK̂I= α= 0, ℋ₁ and ℋ₂ have their common point at infinity, the curves C₁, C₂, C₃, then have two common tangents.

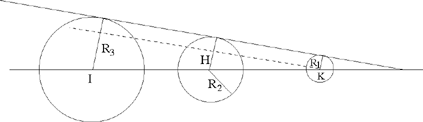
Fig 2.34

As we have seen, this special case with collinear centres was not considered by Ibn al-Haytham, who supposes that KHI is a true triangle. The investigation of the intersection of ℋ₁ and ℋ₂ then becomes complicated. We can, however, reduce this investigation to that of the intersection of a straight line Δ and a branch of a hyperbola, using an algebraic method.

Let there be an orthonormal coordinate system (Kx, Ky); let us put 0 < HK̂I < π. We have K (0, 0), H (d₃, 0), I (d₂ cos α, d₂ sin α), L (x, y).

Fig. 2.35

Thus, the data satisfy the inequalities

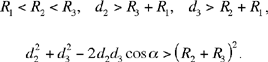
The circle C (L, r) is a solution to the problem if and only if

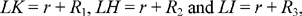
hence

(1)

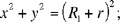
(2)

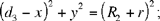
(3)

From (1) and (2) we obtain

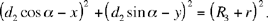
(4)

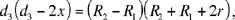
and from (4) we have

From (1) and (3) we obtain

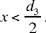
(5)

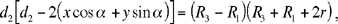
and from (5) we have

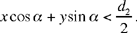
From (4) we obtain

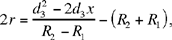
hence

6)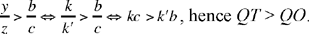

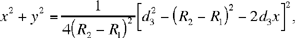
From (1) and (6) we obtain

which can be rewritten

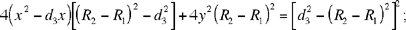
hence

7)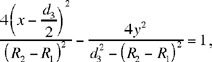

the equation of the hyperbola ℋ₁ with centre 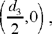foci K and H and transverse axis (R₂ – R₁).

From the condition 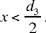, the point L lies on the branch of ℋ₁ that passes round the focus K.

From (4) and (5) we obtain

8)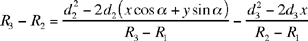

which is the equation of the straight line Δ.

We may note that by eliminating r between (1) and (5), we find the equation of ℋ₂ with axis KI and foci K and I, which can be written

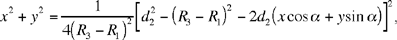
where 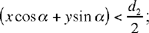or again

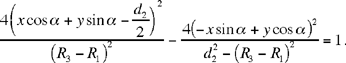
Eliminating x² + y² between the equations of ℋ₁ and ℋ₂ give us back the equation of the straight line Δ.

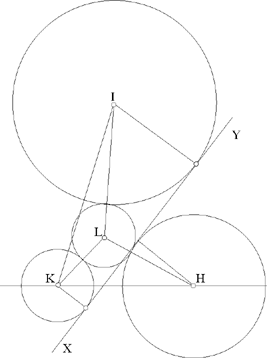
Fig. 2.36

Now, the investigation of Δ and ℋ₁ brings in six parameters: R₁, R₂, R₃, d₂, d₃ and α. We shall not present it here. Let us note, however, that if Δ is parallel to an asymptote, Δ and ℋ₁ have one common point at infinity; to this point there corresponds a straight line tangent to the three given circles. This is, for example, the case in Figure 2.36, in which the circle L, on the one hand, and the straight line XY, on the other, are tangents to the three given circles. This straight line corresponds to the case in which, in Figure 2.14, the point L₁ recedes to infinity.

Algebraic commentary on the auxiliary problem

The algebraic reading of the auxiliary problem is not from Ibn al-Haytham. It allows us to look at his text in a different way, which might shed light on its development.

Let us set out with the same data as before. We are presented with several cases for the figure, according to the positions of S and O with respect to K on the straight half line [UK) and the straight half line [QK), respectively. In all the cases for the figure, we can write

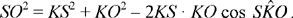
Let us put SO = x, US = y, OQ = z, (where x, y, z are positive unknowns), hence

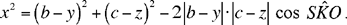
If b – y and c – z have the same sign, SK̂O = α, and if b – y and c – z have opposite signs, SK̂O = π – α, so, in every case, x, y, z satisfy

(1)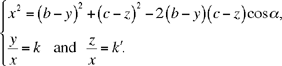

Eliminating y and z gives

(2)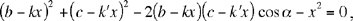

and if we make use of a²= b² +c² –2bc cos α, (2) can be rewritten

(3)

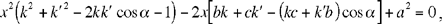
an equation whose discriminant is

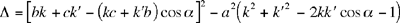
which, after manipulation and simplification, can be rewritten

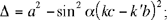
hence

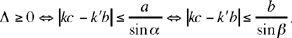
1.

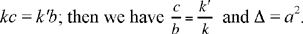
Let us put 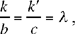hence k = λb and k’ = λc; from (2) we have

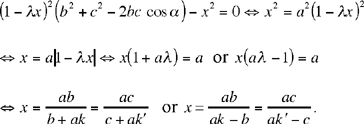
The first root gives a solution for any value of k; the second gives a solution if 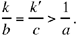So the problem has at least one solution; it will have a second one if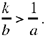

We may note that 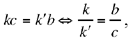now 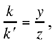hence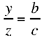

which implies SO || UQ; so this case corresponds to Ibn al-Haytham’s case I.

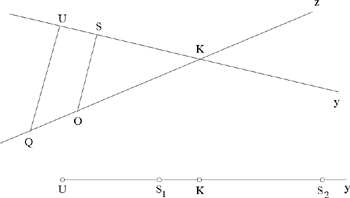
Fig. 2.37

2.

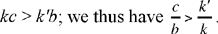
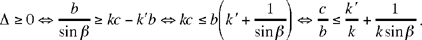
3.

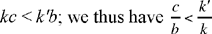
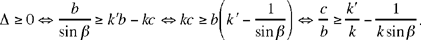
From 1, 2 and 3, it follows that

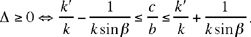
If this double condition is satisfied, the equation has two roots or one double root, but these roots do not provide solutions of the initial problem unless they are positive, which introduces discussions that we shall not enter into here.

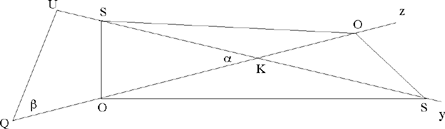
Fig. 2.38

Let us, however, examine the special cases in which one of the points, S or O, is identified with the point K. The equations (1), (2) or (3) still

apply; from which we obtain:

•

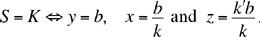
From (2) we shall have S = K if and only if

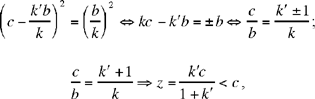
so O lies on [QK);

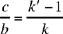
then does not give a solution unless k’ > 1; we then have

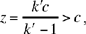
the point O lies on [K, z).

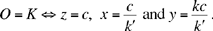
From (2) we shall have O = K if and only if

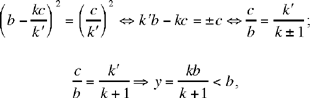
so S lies on [UK);

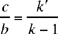
does not give a solution unless k > 1; then we have

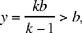
the point S lies on [Ky).

We have just seen that equation (3) has the root 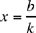when 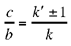and has the root 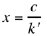when 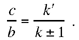. So in each of these four eventualities it has a second root that is obtained, for example, by using the product of the roots 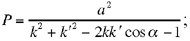the second root does not lead to a solution to the problem unless we have

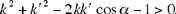
To sum up, we find both cases Ibn al-Haytham investigated and special cases to which he did not draw attention.

____________________

¹ R. Rashed and H. Bellosta, Ibrāhīm ibn Sinān: Logique et géométrie au X^e siècle, Leiden, 2000, pp. 627–35.

² Ibid., p. 633.

³ See p. 249.

⁴ See p. 250.

⁵ Apollonius, Les Coniques, Tome 2.1: Livres II et III, commentaire historique et mathématique, édition et traduction du texte arabe par R. Rashed, Berlin, 2010; Apollonius de Perge, La section des droites selon des rapports, commentaire historique et mathématique, édition et traduction du texte arabe par Roshdi Rashed et Hélène Bellosta, Berlin, 2009; R. Rashed and H. Bellosta, Ibrāhīm ibn Sinān: Logique et géométrie au X^e siècle, pp. 131–3.

⁶ Al-Qūhī considers the same problem in his text The Book of the Centres of Tangent Circles that Lie on Lines by the Method of Analysis, ms. Paris, BN 2457, fols 19^r–21^r. He considers two cases: circles that make exterior contact and circles that make interior contact. See P. Abgrall, ‘Les cercles tangents d’al-Qūhī’, Arabic Sciences and Philosophy, 5.2, 1995, pp. 263–95.

⁷ See p. 264.

⁸ See p. 264.

⁹ See p. 268.

¹⁰ See F. Woepcke, ‘Notice sur une théorie ajoutée par Thābit Ben Qorrah à l’arithmétique spéculative des grecs’, Journal Asiatique, IV, 2, 1852, pp. 420–9; R. Rashed, ‘Nombres amiables, parties aliquotes et nombres figurés aux XIII^e et XIV^e siècles’, Archive for History of Exact Sciences, 28, 1983, p. 107–47; repr. in Entre arithmétique et algèbre: Recherches sur l’histoire des mathématiques arabes, Paris, 1984, pp. 259–99.

¹¹ A. Anbouba, ‘Un traité d’Abū Ja‘far al-Khāzin sur les triangles rectangles numériques’, Journal for the History of Arabic Science, 3.1, 1979, pp. 134–78, esp. p. 157.

¹² R. Rashed, ‘Ibn al-Haytham et le théorème de Wilson’, Archive for History of Exact Sciences, 22.4, 1980, pp. 305–21; repr. in Entre arithmétique et algèbre, pp. 227–43 and ‘Ibn al-Haytham et les nombres parfaits’, Historia Mathematica, 16, 1989, pp. 343–52; repr. in Optique et mathématiques: Recherches sur l’histoire de la pensée scientifique en arabe, Variorum CS388, Aldershot, 1992, XI.

¹³ R. Rashed, ‘Nombres amiables, parties aliquotes et nombres figurés’.

¹⁴ J. L. Coolidge, A History of Geometrical Methods, Oxford, 1940; repr. Dover, 1963, pp. 51–2.

¹⁵ See, for example, P. Ver Eecke’s introduction to his translation of Apollonius’ Conics, Paris, 1959, pp. XXV–XXX.

¹⁶ Al-Nadīm, Kitāb al-fihrist, ed. R. Tajaddud, Teheran, 1971, p. 326.

¹⁷ Pappus d’Alexandrie, La Collection mathématique, French trans. Paul Ver Eecke, Paris/Bruges, 1933, II.2, p. 483.

¹⁸ Les Coniques d’Apollonius de Perge, trans. Paul Ver Eecke, p. XXVI.

¹⁹ We may note that al-Nadīm attributes to the astronomer and mathematician Ḥabash al-Ḥāsib (still alive in 859) a book with the title Book on Three Tangent Circles and How the Contact is Made (Kitāb al-dawā’ir al-thalāth al-mutamāssa wa-kayfiyya al-ittiṣāl), p. 334.

²⁰ R. Rashed and H. Bellosta, Ibrāhīm ibn Sinān: Logique et géométrie au Xe siècle, p. 12.

²¹ Ibid., p. 16.

²² Ibid., Chap. V.

²³ See R. Rashed and H. Bellosta, Ibrāhīm ibn Sinān: Logique et géométrie au Xe siècle, Chap. V.

²⁴ See p. 199.

²⁵ Let us take up this discussion again using a different method:

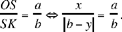
• If 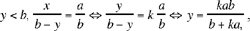which gives 0 < y < b, hence the solution:

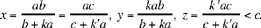
That solution gives S₁ on [UK ] and O₁ on [QK]; it exists for any value of k and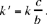

• If 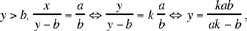we need 0 < y, hence the condition 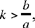hence 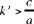because by hypothesis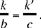

If this condition is satisfied, we have the solution:

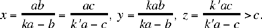
This solution gives S₂ on the straight half line [UK) beyond K, and O₂ on the straight half line [QK) also beyond K. This solution exists only if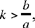
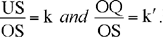
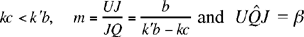