In the name of God the Compassionate the Merciful From Him comes success
TREATISE BY IBN AL-HAYTHAM
On the Properties of the Triangle in Regard to Height
The ancient geometers examined the properties of the equilateral triangle. It thus became clear to them that for any given point on one of the sides of the equilateral triangle, if we draw from that point two perpendiculars to the two remaining sides, then their sum is equal to the height of the triangle. They have written this down and proved it in their books. They examined the heights of other triangles and for them they found neither a complete order, nor an arrangement and thus they did not give any account of them. Since this was how matters stood, necessity encouraged us to investigate the properties of triangles; then we found a uniform order for the heights of the isosceles triangle, and we similarly found an order for the heights of the scalene triangle and a uniform arrangement. When this became clear to us, we composed this treatise.
We first present what the ancients said about the properties of the heights of the equilateral triangle.1 We then move on with what we ourselves have determined about the properties of the heights of other triangles so that the properties of the heights of all triangles might be gathered together in this treatise.
<I> What the ancients said is as follows. For any equilateral triangle, if on one of its sides we take a point from which we draw the perpendiculars to the other two sides, then their sum is equal to the height of the triangle.
Example: The triangle ABC is equilateral; on the side AB we take a point D, from this we draw the perpendiculars DE and DG and we draw the height AH; then the sum of the two perpendiculars DE and DG is equal to the height AH.

Fig II.3.2.1
Proof: Let us draw from the point D a straight line parallel to the straight line BC; let it be DIK. The triangle ADK is equilateral because it is similar to the triangle ABC, so the perpendicular DG is equal to the perpendicular AI and the perpendicular DE is equal to the perpendicular IH, so <the sum> of the perpendiculars DE and DG is equal to the height AH. This is what we wanted.
<II> The ancients also said that if we take a point inside an equilateral triangle and if we draw from this point perpendiculars to the sides of the triangle, then the sum of these perpendiculars is equal to the height of the triangle.
Example: The triangle ABC is equilateral; inside if we take a point D from which we draw the perpendiculars DE, DG and DH and we draw the height AI, then the sum of the perpendiculars DE, DG and DH is equal to the height AI.

Fig II.3.2.2
Proof: We draw from the point D a straight line parallel to the straight line BC; let it be KML. Then the triangle AKL is equilateral, so the sum of the two perpendiculars DH, DG is equal to the perpendicular AM, as before; but the perpendicular DE is equal to MI, so the sum of the perpendiculars DE, DG, DH is equal to the height AI.
This is what the ancients said about this idea (ma‘nā).2 As for what we ourselves have determined, this is what we shall now describe.
<1> For any triangle, if we draw from its angles the perpendiculars to its sides, then the ratio of the perpendicular to the perpendicular is the inverse of the ratio of the side to the side.
Example: In the triangle ABC we have drawn the perpendiculars AD, BE and CG.
I say that the ratio of the perpendicular AD to the perpendicular BE is equal to the ratio of AC to CB and that the ratio of the perpendicular AD to the perpendicular CG is equal to the ratio of AB to BC.

Fig II.3.2.3a
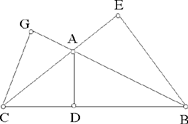
Fig II.3.2.3b
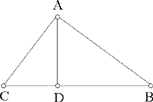
Fig II.3.2.3c
Proof: Each of the angles D and E is a right angle and the angle ACD is common, so the triangle ACD is similar to the triangle BCE, so the ratio of AC to CB is equal to the ratio of AD to BE. In the same way, we prove that the ratio of AB to BC is equal to the ratio of AD to CG. If the triangle has acute angles, all three of the feet of the perpendiculars are inside the triangle,3 as in the first case of the figure.
If the triangle has an obtuse angle, then one of the perpendiculars lies inside the triangle and the other two perpendiculars are outside the triangle, as in the second case of the figure.
If the triangle is right-angled, then the two perpendiculars drawn from the two acute angles are the two sides of the triangle that enclose the right angle, so the feet of the perpendiculars, which are G and E, are at the point A, as in the third case of the figure.
We prove this proposition using a different proof. The product of each of the sides and the perpendicular that falls on it is twice <the area> of the triangle, so the ratio of each of the sides of the triangle to another side is the ratio of the perpendicular that falls on the second side to the perpendicular that falls on the first side. This is what we wanted to prove.
<2> In the same way, if in a scalene right-angled triangle we draw from its right angle the perpendicular to the base, then we cut off from the greater of the two parts of the base a part equal to the smaller one; if we join its endpoint to the right angle with a straight line, then we divide the angle that remains over from the right angle into two halves, then the part cut off from the base between the straight line that divides the angle that remains and the foot of the perpendicular is equal to the height.
Example: Let there be the triangle ABC whose angle A is a right angle; we draw from this the perpendicular AD, we cut off DE equal to DC, we join AE, we divide angle BAE into two halves with the straight line AG.
I say that GD is equal to DA.
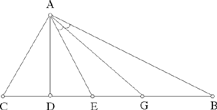
Fig II.3.2.4
Proof: The angle EAD is equal to the angle DAC, so the angle EAD is half the angle EAC. But the angle EAG is half the angle EAB, so the angle GAD is half the angle BAC. But the angle BAC is a right angle, so the angle GAD is half a right angle; but the angle ADG is a right angle, so the angle AGD is half a right angle, so the straight line GD is equal to the straight line DA. This is what we wanted to prove.
<3> If on the base of an isosceles triangle we take an arbitrary point, from which we draw the perpendiculars to the two [equal] sides of the triangle, then their sum is equal to the perpendicular drawn from one endpoint of the base to the side of the triangle, whether the angle of the triangle enclosed by the two equal sides be acute, obtuse or a right angle.
Example: Let there be the isosceles triangle ABC whose sides AC and BA are equal and whose base is BC. On the base BC we take a point D from which we draw the two perpendiculars DE and DG.
I say that their sum is equal to the perpendicular CH.

Fig II.3.2.5a
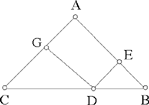
Fig II.3.2.5b

Fig II.3.2.5c
Proof: The two angles B and C are equal, the two angles E and G are equal because they are right angles, so the two triangles BED and DGC are similar and the ratio of CD to DB is equal to the ratio of GD to DE. By composition, the ratio of the sum of GD and DE to DE is equal to the ratio of CB to BD. But the ratio of CB to BD is equal to the ratio of CH to DE,4 so the ratio of the sum of GD and DE to DE is equal to the ratio of CH to DE, so the sum of the two perpendiculars GD and DE is equal to the perpendicular CH.
This proof is the same whatever the properties of the triangle. This is what we wanted.
<4> In the same way, we return to the figure and the given point on the side AB; let it be D. We draw the perpendiculars DG and DH, we draw the perpendicular AE, we put the ratio of AB to BD equal to the ratio of AE to EI and we put the ratio of AI to IL equal to the ratio of AC to CB.
I say that the sum of the perpendiculars DG and DH is equal to the perpendicular LE.
Proof: We join DI and we extend it to K, then DK is parallel to the straight line BC. But since the ratio of AB to BD is equal to the ratio of AE to EI, then the ratio of AC to CB is equal to the ratio of AK to KD. But the ratio of AC to CB is equal to the ratio of AI to IL, so the ratio of AK to KD is equal to the ratio of AI to IL. But the ratio of AK to KD is equal to the ratio of AI to DH, as has been proved in Proposition 3 of this treatise. So the perpendicular DH is equal to LI and DG is equal to EI, so <the sum> of the perpendiculars DG and DH is equal to the perpendicular LE. This is what we wanted to prove.

Fig II.3.2.6a

Fig II.3.2.6b

Fig II.3.2.6c
<5> In the same way, we return to the isosceles triangle; let the point lie inside the triangle. Let there be the triangle ABC and the point D which is inside the triangle; let us draw from this point the perpendiculars DE, DG, DH. We draw from the point D a straight line parallel to the straight line BC; let it be MDL. We draw the perpendicular AIK and let us put the ratio of AI to IN equal to the ratio of AB to BC, which is equal to the ratio of AM to ML.
I say that the sum of the perpendiculars DE, DG and DH is equal to the perpendicular NK.
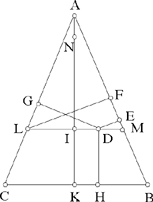
Fig II.3.2.7a
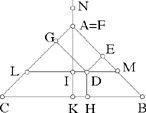
Fig II.3.2.7b
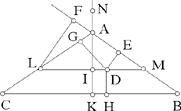
Fig II.3.2.7c
Proof: We draw the perpendicular LF. Since the ratio of AI to IN is equal to the ratio of AM to ML, we have IN equal to LF. Now we have proved that the sum of the perpendiculars DE and DG is equal to the perpendicular LF. <The sum> of the two perpendiculars DE and DG is thus equal to the perpendicular NI and the perpendicular DH is equal to the perpendicular IK, so the sum of the three perpendiculars DE, DG and DH is equal to the perpendicular NK. This is what we wanted to prove.
This proof is the same for all isosceles triangles, whether they are acute-angled, or have an obtuse angle or a right angle.
<6> In the same way, we return to the isosceles triangle; let the triangle be ABC. We divide the angle ABC into two halves with the straight line BE, we draw EH parallel to the base BC and we draw the perpendicular AGD.
I say that if from a given point on the straight line EH we draw two perpendiculars to the straight lines AE and AH, then their sum is equal to the perpendicular GD. On the straight line EH we take a point I from which we draw the perpendiculars IK and IL. I say that the sum of IK and IL is equal to the perpendicular GD.

Fig II.3.2.8
Proof: We draw the perpendicular EM. Since EH is parallel to the straight line CB, the angle HEB is equal to the angle EBC. But the angle EBC is equal to the angle EBH, so the angle HEB is equal to the angle EBH; so the straight line EH is equal to the straight line HB. So the ratio of AH to HB is equal to the ratio of AH to HE; but the ratio of AH to HB is equal to the ratio of AG to GD and the ratio of AH to HE is equal to the ratio of the perpendicular AG to the perpendicular EM,5 so the ratio of AG to GD is equal to the ratio of AG to EM and the perpendicular EM is equal to GD; but the perpendicular EM is equal to the sum of the perpendiculars IK and IL, as before.6 The sum of the two perpendiculars IK and IL is thus equal to the perpendicular GD.
This proof is the same for all isosceles triangles.
<7> For any acute-angled isosceles triangle, the excess of its side – one of the two <equal> sides – over its height – the one that falls on this side – the excess of this height over the segment that it cuts off on the side towards the base and twice this segment are all three in continued proportion.
Let there be a triangle ABC whose sides AB and AC are equal and whose three angles are acute. Let us draw in this triangle the perpendicular CE.
I say that the excess of AB over CE, the excess of CE over EB and twice EB are all three in continued proportion.

Fig II.3.2.9
Proof: We draw the perpendicular AD and the perpendicular DH, which makes7 HE equal to HB. We join ED and let us divide the angle ADE into two halves with the straight line DG, then GH is equal to HD, as we have proved in Proposition 4 of this treatise.8 Since CB is twice BD and EB is twice BH, CE is parallel to DH and is twice DH. Since the product of AH and HB is equal to the square of HD, the product of AH and HE is equal to the square of HG, so the ratio of AH to HG is equal to the ratio of HG to HE and is equal to the ratio of AG to GE.9 But HG is greater than HE, because GH is greater than HB. But given that AD is greater than DB; the angle BAC is in fact acute, so the straight line AG is greater than the straight line GE. We put GI equal to GE, then the ratio of AG to GI is equal to the ratio of GH to HE, so the ratio of AI to IG is equal to the ratio of GE to EH, so the product of AI and HE is equal to the square of GE, twice the product of AI and HB is equal to twice the square of EG and twice the product of AI and BE is equal to the square of EI. Since GE is equal to GI and EH is equal to HB, thus IB is twice HG. But HG is equal to HD and CE is twice HD, so the straight line IB is equal to the perpendicular CE, thus AI is the excess of AB over the perpendicular CE. But IB is equal to the perpendicular CE and IE is the excess of IB over EB. Now AI, IE and twice EB, which is the part cut off by the perpendicular CE, are in continued proportion, so the excess of AB over the perpendicular CE, the excess of the perpendicular CE over EB – which is the part that it cuts off on the side <AB> – and twice EB are all three in continued proportion. This is what we wanted to prove.
<8> In the same way, let the scalene triangle be ABC; on any one of its sides, let us take a point; let it be the point D. Let us draw from the point D the two perpendiculars DE and DG. We draw the perpendicular BH, we draw DKI parallel to the straight line AC and we put the ratio of BK to KN equal to the ratio of BC to CA.
I say that the sum of the perpendiculars DE and DG is equal to the perpendicular NH.

Fig II.3.2.10
Proof: The ratio of BI to ID is equal to the ratio of BC to CA; but the ratio of BC to CA is equal to the ratio of BK to KN, so the ratio of BI to ID is equal to the ratio of BK to KN. But the ratio of BI to ID is equal to the ratio of BK to DG, so the perpendicular DG is equal to the perpendicular KN and the perpendicular DE is equal to the perpendicular KH. So the sum of the perpendiculars DG and DE is equal to the perpendicular NH. This is what we wanted to prove.
<9> Let us return to the scalene triangle; let it be ABC. Let us take an arbitrary point D inside it. Let us draw from this point the perpendiculars DE, DG, DH. We cause to pass through the point D a straight line parallel to the straight line BC; let it be LDM. We draw the perpendicular AIK and we put the ratio of AI to IN equal to the ratio of BC to CA.
I say that the sum of the three perpendiculars DE, DG and DH is equal to the perpendicular NK.

Fig II.3.2.11
Proof: The ratio of LM to MA is equal to the ratio of BC to CA; but the ratio of BC to CA is equal to the ratio of AI to IN, so the ratio of AI to IN is equal to the ratio of LM to MA. The sum of the perpendiculars DE and DG is thus equal to the perpendicular NI, as it was proved earlier. Now the perpendicular DH is equal to the perpendicular IK, so the sum of the perpendiculars DE, DG and DH is equal to the perpendicular NK.
This proof is the same for any triangle, right-angled, acute-angled or with an obtuse angle, scalene, isosceles or equilateral. This is what we wanted to prove.
The treatise on the heights of triangles is complete.
Thanks be given to God and blessings upon our Prophet Muḥammad and those that are His.
I completed transcribing it at Mosul, the Protected city, in the month Ṣafar 632.
_______________
1 See Appendix, Text 4: Two Propositions of the Ancients.
3 They lie on the sides of the triangle and not on their extensions.
4 Because the triangles BDE and BCH are similar.
5 Proposition 1.
6 Proposition 3.
7 In the manuscript, we read ‘and we make’.
8 In fact, ADB is right-angled and scalene.
9 See commentary, p. 463.