LETTER OF AḤMAD IBN MUḤAMMAD IBN ‘ABD AL-JALĪL <AL-SIJZĪ> TO THE PHYSICIAN ABŪ ‘ALĪ NAẒĪF IBN YUMN
On the Construction of an Acute-angled Triangle from Two Unequal Straight Lines
You have asked – may God give you continuing happiness – to construct an acute-angled triangle from two unequal straight lines; and you mentioned that Abū Sa‘d al-‘Alā’ ibn Sahl constructed this by using an ellipse with the help of proposition fifty-two of Book III of Apollonius’ Conics,1 by the method of division and discussion. I remember that I had a solution to the problem, and it is in our book on Triangles. But what we have presented in our book was not [done] by the method of discussion. So I have found it by the method of discussion and division starting from the first and third books of Euclid’s Elements so as to prove to you – may God sustain you – that the propositions established by simple methods and principles that can be found from the books of Euclid’s Elements are preferable to adopting difficult methods, and in particular those of the Conics. For problems whose solutions cannot be established from the book of the Elements, one is allowed to have recourse to unusual and obscure methods; but we do not need to show what they can do, because it is obvious; and from God comes help.
Question: Starting from two given unequal straight lines, we wish to construct an acute-angled triangle.
Answer: For this triangle there are three cases. Let the two given straight lines be the straight lines AB, AC. We want what we have said. We draw a circle on the chord AB such that the arc AB is intercepted by half a right angle; which is the circle ADB. We draw BD perpendicular to AB to meet the circumference of the circle. We join AD. It is clear that AD is a diameter of the circle. With centre A and distance AC, we draw the circular arc CK. Either it will touch the circle ADB at the point D, as in the first case; or it will cut it in two points – in I and K – as in the second case; or it will lie outside the circle, as in the third case. If it lies outside the circle, let us extend BD to I and let us join AI.2 If it cuts it as in the second case, let it cut it in two points on either side of the diameter AD, at the points I and K. Let us then join AI. If it touches it, as in the first case, it is necessary that it touches it at the point D.
I say that the angle subtended by the straight line AB3 always lies inside the sector CAD, in the first case, inside the sector CAI, in the second case and the third case. Now, from the two straight lines drawn from the points A and B to the arc CED,4 and if we draw a straight line from the point B to the straight line drawn from A to the arc CED, such that, with the straight line drawn from B to the arc CED, this straight line encloses an angle equal to the angle formed on the arc CED by the two straight lines drawn from the points A and B, there is formed5 an acute-angled triangle. But it is not possible to construct an acute-angled triangle from these two given straight lines by anything other than this.
Let us draw AE to meet the arc CED and let us join BE. On the point B of the straight line AB we construct an angle equal to the angle AEB; let it be <the angle> EBG.
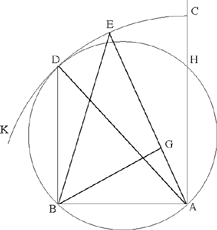
Fig. 1
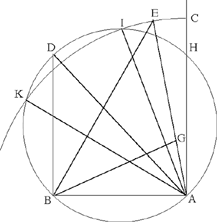
Fig. 2
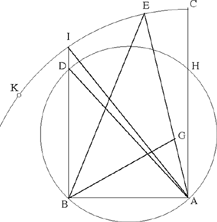
Fig. 3
I say that the triangle AGB is acute-angled.
Proof: Since the angle AEB is smaller than half a right angle, and the angle AGB is double the angle AEB, because it is equal to the sum of the two angles AEB and EBG which are equal to one another, accordingly the angle AGB is smaller than a right angle; so it is acute; but since the two straight lines drawn from the points A and B to meet the arc CED enclose with the straight line AB two angles each smaller than a right angle, that is to say acute, accordingly each of them6 is acute; so the triangle AGB is acute-angled. It is clear that the straight line drawn from the point A in the direction of H encloses an obtuse angle with AB. Similarly, the straight line drawn from B in the direction of D encloses an obtuse angle7 with AB. So take the triangle inside the straight lines AC and BD which are parallel. This is what we wanted to prove.
This is what we have presented by means of division and discussion, employing a universal method, whose easy access, simple course and brevity of expression make it agreeable to your mind and to your understanding. So take profit from it, may God make you happy through it and let there be peace.
The treatise is completed, thanks to God and to His blessings.
I wrote it on Thursday, the day day of the month of Ābān in the year 339 in the era of Yazdegerd.8
______________
1 Lit.: the cone.
2 In the last two cases of the figure, al-Sijzī uses the same letter, I, to designate two different points.
3 He implies that E, the vertex of the angle AEB subtended by the straight line AB, always lies on the arc CD (excluding its endpoints) in the first case, and on the arc CI (excluding its endpoints) in the second case and the third case.
4 Al-Sijzī considers the first case of the figure where E is on the arc CD. In the second and third cases, we need E to lie on the arc CI; the arc CED exists only in the first case of the figure, and in what follows al-Sijzī deals with the first case.
5 Lit.: closes up.
6 Here, ‘them’ refers to the three angles.
7 He means: in separating from AH and BD.
8 See History of the texts, p. 577, n. 46.