TWO PROPOSITIONS OF THE ANCIENTS ON THE PROPERTY OF THE HEIGHTS OF AN EQUILATERAL TRIANGLE: PSEUDO-ARCHIMEDES, AQĀṬUN, MENELAUS

Book by Archimedes on the Foundations of Geometry, translated from Greek into Arabic by Thābit ibn Qurra, for Abū al-Ḥasan ‘Alī ibn Yaḥyā, protected by the Prince of Believers

 

– I – Let us take an equilateral triangle ABC, in it let us draw the height AD and on the straight line BD let us mark an arbitrary point, which is the point E. From the point E let us draw two perpendiculars to the straight lines CA and AB, which are the straight lines GE and EH.

I say that the straight line AD is equal to the sum¹ of the straight lines GE and EH.

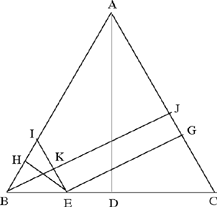
Proof: From the point E let us draw a straight line parallel to AC, which is the straight line EI. From the point B let us draw a straight line perpendicular to the straight line AC, which is the straight line BJ. It being given that the triangle ABC is equilateral and that the straight line AC is parallel to the straight line IE, the triangle BIE is equilateral; and it being given that the straight line BJ is perpendicular to the straight line AC and that the straight line AC is parallel to the straight line IE, the straight line BK is perpendicular to the straight line IE. Now the straight line KJ is equal to the straight line EG, because the surface KEGJ is a parallelogram. So the whole straight line BJ is equal to the sum of the straight lines EH and GE; but the straight line BJ is equal to the straight line AD, so the straight line AD is equal to the sum of the straight lines EG and EH. This is what we wanted to prove.

 

– II – Let us take an equilateral triangle ABC, let us draw inside it the height AD and let us mark inside it an arbitrary point, which is the point E. From this point let us draw perpendiculars to the sides of the triangle, which are the straight lines GE, EH and EI.

I say that AD is equal to the sum of the straight lines EG, EH, EI.

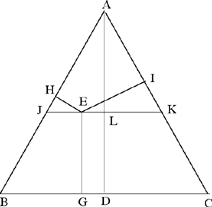
Proof: From the point E let us draw a straight line parallel to the straight line BC, which is the straight line JELK. It being given that the straight line JK is parallel to the straight line BC and that the straight line EG is parallel to the straight line DL, accordingly the surface ED is a parallelogram. It being given that the triangle ABC is equilateral and that we have drawn the height AD and the straight line JK parallel to its base, which is the straight line BC, the triangle AJK is equilateral. And it being given that the triangle AJK is equilateral, that we have drawn the height AL, that on the straight line BK we have marked an arbitrary point – which is the point E – and that from this point we have drawn two perpendiculars to the straight lines JA, AK which are the straight lines EH, EI, accordingly the straight line AL is equal to the sum of the straight lines EH, EI. Now we have proved that the straight line LD is equal to the straight line EG, so the straight line AD is equal to the sum of the straight lines EG, EH, EI. This is what we wanted to prove.

Book of Hypotheses by Aqāṭun

 

– I – Let us take an equilateral triangle ABC in which we draw the height AD and mark an arbitrary point on the straight line CB, which is the point E. From this point let us draw two perpendiculars to the straight lines CA and AB, which are the straight lines GE and EH.

I say that the straight line AD is equal to the sum of the straight lines GE and EH.

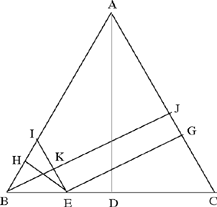
Proof: From the point E we draw a straight line parallel to the straight line AC; let the straight line be IE. From the point B let us draw a straight line perpendicular to the straight line CA; let the straight line be BJ. Since the triangle ABC is equilateral and since the straight line AC is parallel to the straight line IE, the triangle IBE is equilateral. Since the straight line BJ is perpendicular to the straight line AC, which is parallel to the straight line IE, accordingly BK is perpendicular to the straight line IE. Now the straight line EH is perpendicular to the straight line IE, so the straight line BK is equal to the straight line EH; but the straight line KJ is parallel to the straight line EG, so it is equal to it. So the whole straight line BJ is equal to the sum of the straight lines GE and EH. But the straight line BJ is equal to the straight line AD, so the straight line AD is equal to the sum of the straight lines EH and EG. This is what we wanted to prove.

 

 

– II – Let us take an equilateral triangle ABC, let us draw inside it the height AD and inside it let us take an arbitrary point, which is the point E. From this point let us draw three perpendiculars to the sides of the triangle; which are the straight lines EG, EH and EI.

I say that AD is equal to their sum.

Proof: We cause to pass through the point E a straight line parallel to the straight line BC; let it be the straight line JEK. Since the straight line JK is parallel to the straight line BC and since EG is parallel to the straight line DL, accordingly the surface DE is a parallelogram. Since the triangle ABC is equilateral and since the straight line JK is parallel to its base, the triangle AJK is equilateral. Now in it we have drawn the height AL and on the straight line KLJ we have marked a point E from which we have drawn two perpendiculars to the straight lines AJ, AK – let the straight lines be EH and EI –, accordingly the straight line AL is equal to their sum. But the straight line LD is equal to the straight line EG, so the straight line AD is equal to the sum of the straight lines EG, EH, EI. This is what we wanted to prove.

 

 

Treatise by Aḥmad ibn Muḥammad ‘Abd al-Jalīl al-Sijzī on the Properties of the Perpendiculars Dropped from a Given Point onto a Given Equilateral Triangle by the Method of Discussion

 

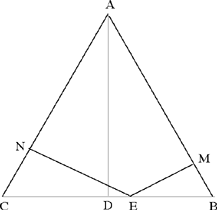
– I – If the point falls on one of the sides of the triangle, like the point E, let us draw the two perpendiculars, EM and EN, to the sides AB and AC. We cannot draw a third perpendicular, apart from these two. Since EM is the height of an equilateral triangle, the side of the triangle is BE and since EN is the height of an equilateral triangle, the side of the triangle is EC. So the ratio of EM to BE is equal to the ratio of EN to EC and is equal to the ratio of AD to BC. By composition, the ratio of the sum of EM and EN to the sum of BE and EC is equal to the ratio of AD to BC, so the sum of the two straight lines EM and EN is equal to the straight line AD.

– II – If the point falls on the straight line AD, like the point G, let us then draw the two perpendiculars GS and GO to the sides AB and AC and let us draw the straight line ZGU parallel to the straight line BC; the sum of the straight lines GS, GO is thus equal to the straight line AG and the sum of the straight lines GS, GO, GD is equal to the sum of AG and GD, that is to say the straight line AD.

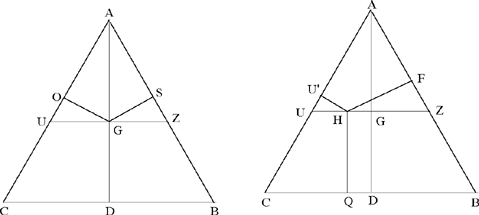
If the point falls in the surface ABC, like the point H, let us then draw the straight line ZHU parallel to the straight line BC and let us draw the perpendiculars HP, HU', HQ to the sides AB, AC, BC. From what we have proved, the sum of the straight lines HP, HU' is equal to the perpendicular AG and the straight line HQ is parallel to the straight line GD and is equal to it, so the sum of the straight lines HP, HU', HQ is equal to the sum of the straight lines AG, GD, that is to say the straight line AD.

 

¹ We sometimes add the word ‘sum’, to conform with the standard usage in English.