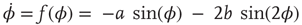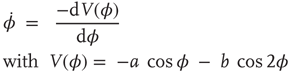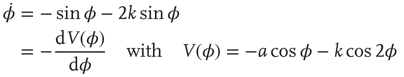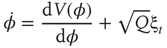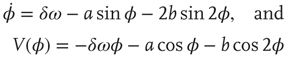4
The Dynamic Brain in Action: Coordinative Structures, Criticality, and Coordination Dynamics

J. A. Scott Kelso

4.1 Introduction

The pairing of meaning and matter is the most profound feature of the world and the clue to understanding not only ourselves but all existence. Science takes the meaning out of matter through the principle of objectivization [1]. Yet, as evolved living things, we all know that meaning lurks behind everything we do. Should science exorcise meaning or try to come to grips with it? And if so, how? The key to understanding meaningful matter as it is manifested in behavior and the brain lies in understanding coordination. Coordination refers not just to matter in motion, nor to complex adaptive matter: it refers to the functional – informationally meaningful – coupling among interacting processes in space and time. Such functional spatiotemporal ordering comes in many guises in living things, from genes to cells to neural ensembles and circuitry to behavior (both individual and group) and cognition. It is a truism nowadays that biological processes, at all scales of observation, are highly degenerate [2] [3] and obey the principle of functional equivalence [4] [5]. Since the late 1970s, an approach grounded in the concepts, methods, and tools of self-organization in physical and chemical systems (synergetics, dissipative structures) yet tailored specifically to the behavioral and neural activities of animate, living things (moving, perceiving, feeling, deciding, thinking, learning, remembering, etc.) has emerged – a theoretical and empirical framework that aims to understand how the parts and processes of living things come together and break apart in space and time. It is called coordination dynamics (e.g., [6–14]). Coordination Dynamics (CD for short) is a line of scientific inquiry that aims to understand how functionally significant patterns of coordinated behavior emerge, persist, adapt, and change in living things in general and human beings in particular. “Laws of coordination” and their numerous mechanistic realizations are sought in a variety of different systems at multiple levels of description. CD addresses coordination within a part or process of a system, between different parts and processes and between different kinds of system (For a trilogy of encyclopedia articles on CD, and the many references contained therein, the reader is referred to Fuchs and Kelso [15], Oullier and Kelso [16], and Kelso [17]; see also Huys and Jirsa [9] for an excellent treatment). CD contains two complementary aspects (“cornerstones,” cf. [11]), that are necessary to understand biological coordination: a spontaneous self-organizing aspect, as we shall see intimately connected to the concepts and empirical facts surrounding phase transitions and critical phenomena in nature's nonequilibrium, highly heterogeneous systems; and information, viewed not as a mere communication channel but as functionally meaningful and specific to the coordination dynamics.

Self-organizing processes and meaningful information in animate, living things are deeply entwined and inseparable aspects of CD. Self-organizing processes create meaningful information in coupled dynamical systems, which in turn are capable of sculpting or guiding the self-organizing dynamics to suit the needs of an organism [18]. In CD, the organism qua agent and the environment are not two separate things, each with their own properties, but rather one single coevolving system (see also [19]). As far as CD is concerned, to refer to a system in its environment or to analyze a system plus an environment, although common in practice, are questionable assumptions. As Poincaré said, many years ago, it is not the things themselves that matter, “but the relations among things; outside these relations there is no reality knowable” (cited in [11], p. 97). “Atoms by themselves, John Slater (1951) remarked, have only a few interesting parameters. It is when they come into combination with each other that problems of real physical and chemical interest arise” (cited in [20], p. 19). For the coordination of the brain and indeed for coordination at all levels, we will have to identify our own informationally relevant structures, our own “atomisms of function.” They will be partly but not totally autonomous, and never context independent. They will be relational and dynamic, evolving on many spatiotemporal scales. Although they will be bounded by levels above and below, on any given level of description they will have their own emergent descriptions [11] [21]. Coordination in living things will have its own geometry, dynamics, and logic that will have to be identified. We explore the ramifications of this in what follows.

4.2 The Organization of Matter

The study of matter has undergone a profound revolution in the past 40 odd years with the discovery of emergent phenomena and self-organization in complex, nonequilibrium systems. One can trace these developments to the work of scientists such as Wilson, Kadanoff, and others in their fundamental research on phase transitions; to crucial extensions of phase transition theory to nonequilibrium systems by “the father of laser theory” Hermann Haken and his generalizations thereof in a field he named Synergetics; to Ilya Prigogine and colleagues for their work on the thermodynamics of chemical reactions and irreversible processes, the “Brusselator” and generalizations thereof to “Dissipative Structures”; to Manfred Eigen and Peter Schuster's autocatalytic cycles and “hypercycles” as necessary underpinnings of prebiotic life. Lesser known, but no less important figures include Arthur Iberall and the field he named Homeokinetics – a kind of social physics in the broadest sense where atomisms at one level create continua at another – an up-down as well as a side to side physics of living things [22] [23]. All the aforementioned – and many others, of course – have, I think, something essential in common: they exemplify a search for the connections between the ways different kinds of processes behave, at many different levels of description and scales of energy, length, and time.¹ They follow, in a sense, whether consciously or not, the goal of identifying principles of organization that transcend different kinds of things. They are reductionists, not (or not only) to elementary entities such as cells, molecules, and atoms, but to finding a minimum set of organizing principles for how patterns in nature form and change.

For a concrete yet conceptually rich example, take the work of the late Kenneth Wilson (1936–2013) who won the Nobel Prize in Physics in 1982 for a quantitative understanding of phase transitions – how matter changes from one form to another. Through his renormalization group and block spin methods, Wilson was able to show that many different systems behave identically at critical points: whether a ferromagnet changing its magnetization at a critical temperature (the reciprocal of the coupling strength between its elements) or a fluid hovering between its liquid and vaporous state. Wilson envisaged the transformation of the system from one state to another as the motion of a marble rolling on a surface constructed in an imaginary multidimensional space: the system's parameter space (Figure 4.1). Each frame of motion reveals the effect of his mathematical method (the so-called block spin transformation). This transformation allows the marble to move but the speed and direction of the marble are dictated by the slope of the surface. Knowing the slope of the surface as the system approaches the critical point, one can calculate how the properties of the system vary as the coupling strength between the block spins changes – precisely the information one needs to understand critical phenomena.

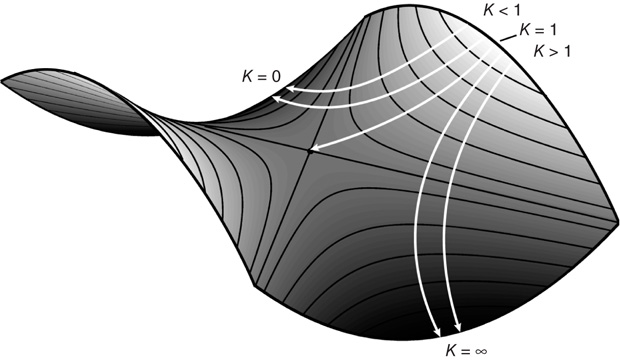
Figure 4.1 The renormalization group transformation can be described as the motion of a point on a surface constructed in a multidimensional parameter space. The form of the surface is defined by all the couplings between block spins, but only nearest-neighbor coupling, K, is shown here. The surface has two peaks and two sinkholes, which are connected to a saddle point. The saddle defines the system's critical point. (Adapted from Wilson [24].) See text for details.

The test, of course, of any good theory is how it matches (and even predicts) experimental data; in the case of phase transitions, the data base is very rich indeed. Imagine what the early humans must have felt when they heated up water and it turned into vapor or during the winter when the ponds outside their caves turned into ice. Measurable macroscopic properties of a ferromagnet, such as its spontaneous magnetization or in the case of a fluid the density difference between the liquid and vapor phases, are called order parameters. A magnet's susceptibility (meaning how the magnetization changes for a small change in an applied magnetic field) or the compressibility of the fluid (how density changes with changes in pressure) all exhibit the same critical behavior. In the case of the ferromagnet, the order parameter, its susceptibility, and its correlation length (a measure of fluctuations) are all functions of how much the temperature deviates from the critical temperature. On an ordinary temperature scale, different systems have different critical temperatures. However, by simply expressing the actual temperature T (which we may call a control parameter) and the critical temperature T_c as a ratio, t = (T − T_c)/T_c, all critical points are the same. That is, the macroscopic properties of different systems are proportional to the absolute value of t raised to some power. This means that to properly characterize critical phenomena in thermodynamic systems, one needs to determine what that power is, that is, the value of the critical exponents. Wilson showed that fluids and ferromagnets lie on the same surface in parameter space (Figure 4.1) and, although they start with different initial positions, both converge on the same saddle point and hence have the same critical exponents. This similarity in the critical behavior of fluids and ferromagnets attests to the more general principle of universality: fluids, long chain polymers, alloys, superfluids like helium 4, even mixtures of liquids such as oil and water all belong to the same universality class.

My purpose in saying something about Wilson's work is certainly not to “physicalize” neural and behavioral systems. Analogy is often useful in science and sometimes leads to important insights. In this case, analogy leads us to inquire if the theoretical concepts and methods used to understand collective or cooperative behavior in nature may enable us to better understand the brain and its relation to what people do. With its billions of neurons, astrocytes, and vast connectivity, does the brain exhibit collective behavior and phase transitions? Important though it may be to study the many varieties of neurons and their molecular and atomic constituents as individual entities, is the emergence of collective or coordinative behavior a fundamental aspect of brain and behavioral function? Once one grasps the analogy, the answer might seem as obvious as an apple falling from a tree, but we cannot assume it to be so. One message from studies of cooperative phenomena in physics is that we have come to appreciate what the relevant macroscopic variables such as pressure, volume, temperature, and density are and how they relate lawfully. We also know that many parameters in physical systems are irrelevant and have no effect whatsoever on how the system behaves. The numerous different crystalline structures in ferromagnets, for example, exhibit the same critical behavior. In complex nervous systems, with very many variables and high-dimensional parameter spaces, it is difficult to tell the wheat from the chaff. In complex nervous systems, neither the order parameters nor the control parameters are known in advance, never mind their lawful relationship.

Although some of the same concepts of phase transitions in physical systems at thermodynamic equilibrium are useful, entirely new methods and tools are needed to handle phenomena associated with nonequilibrium phase transitions [25]. The latter occur in open systems whose internal and external components form a mutually coupled dynamical system. In his influential little book, “What is Life?” written in Dublin in 1943, Schrödinger noted that the enormously interesting disorder–order transitions studied by physicists (as in the case of ferromagnetism where matter changes its structure as temperature is lowered) are irrelevant to the emergence of life processes and the functioning of living things. Without a metabolism, for example, a living system cannot function. Without exchanges of energy, matter, or information with their surroundings, living things can maintain neither structure nor function. We will go into these ramifications a little further later. In actual fact, viewed through a certain lens, the entire range of transition behavior (order to order, order to disorder, disorder to order), resulting phases, and the many mixtures thereof can be observed in biological coordination in different systems.

Whether patterns of coordination emerge as collective effects in nervous systems composed of a large number and variety of heterogeneous microscopic components and connections is an open question.² Are phase transitions and criticality even relevant in neurobehavioral complex systems? Is there any reason to think that the brain, body, and environment are fundamentally self-organized? If such a complex system is governed by laws of coordination dynamics, how would we even go about establishing that? What are these putative laws and what are their consequences for the ways we investigate complex systems such as the brain? Further, what are the implications for understanding, in the words of President Obama when he unveiled the BRAIN initiative to the National Academy of Sciences in April 2013, “who we are”: the profound challenge of understanding “the dynamic brain in action” and what it does – how we move and think and perceive and decide and learn and remember?

The rest of this chapter elaborates on these issues and tries to provide some initial answers. As just one hint of the mindset that criticality involves, we note that some years ago a book entitled “23 Problems in Systems Neuroscience” [28] appeared containing a chapter entitled “Where are the switches on this thing?” A nice book review was published in the journal Nature with the same title [29]. Here is what is potentially at stake: if brains and behavior are shown to exhibit critical phenomena; if they display quantitative signatures of nonequilibrium phase transitions predicted by specific theoretical models, then they will certainly exhibit switching, but – at least in the first instance – there will be no need to posit switches.

4.3 Setting the Context: A Window into Biological Coordination

We begin with some general but vague principle, then find an important case where we can give that notion a concrete precise meaning. And from that case we gradually rise again in generality…and if we are lucky we end up with an idea no less universal than the one from which we began. Gone may be much of its emotional appeal, but it has the same or even greater unifying power in the realm of thought and is exact instead of vague

[30], p. 6

So where to begin? Definitely close to Weyl's approach in his beautiful book on symmetry quoted here, but not quite. The Editors of this volume have invited me to describe our experimental research on critical fluctuations and critical slowing down in the brain and behavior. In particular, they invite some historical perspective on the Haken–Kelso–Bunz (HKB) model. Judged in light of recent research in fields such as ecosystems, climate, and population change, there is much current interest in anticipatory indicators of tipping points ([31] [32]; see [33] commentary). Tipping points, similar to catastrophe theory, are just another catchy word for criticality. Anticipating them is what critical slowing down, enhancement of fluctuations, critical fluctuations, switching time distributions, and so on – that is, quantifiable measures of nonequilibrium phase transitions – are all about.

To put things in a specific context, let us make the familiar strange. Consider an ordinary movement. The human body itself consists of over 790 muscles and 100 joints that have coevolved in a complex environment with a nervous system that contains ∼10¹² neurons and neuronal connections, never mind astrocytes [34]. On the sensory side, billions of receptor elements embedded in skin, joints, tendons, and muscles inform the mover about her movement. And this occurs in a world of light and sound and smell. Clearly, any ordinary human activity would seem to require the coordination among very many structurally diverse elements – at many scales of observation. As Maxine Sheets-Johnstone [35] says in her wonderful book, the primacy of movement for living things has gone unrecognized and unexamined. We come into the world moving. We are never still.

It must be said that physics as the science of inanimate matter and motion has left animate motion virtually untouched.³ It has yet to take the next step of understanding living movement. (Just to be clear, we are not talking about the many useful applications of physics to biological systems, i.e., biophysics, biomechanics, etc.). Rather, what is at issue here is the problem of meaningful movement: the “self-motion,” which the great Newton remarked, “is beyond our understanding” ([36]; see also [37]). Newtonian mechanics defines limits on what is possible at the terrestrial scale of living things, but says nothing about how biological systems are coordinated to produce functionally relevant behavior. If “the purpose of brain function is to reduce the physical interactions, which are enormous in number, to simple behavior” [38], how is this compression to be understood? Instead of (or along with) inquiring how complexity can arise from simple rules [39], we may also ask how an extremely high-dimensional space is compressed into something lower dimensional and controllable that meets the demands of the environment and the needs of the organism. What principles underlie how enormous compositional complexity produces behavioral simplicity? This is a fundamental problem of living movement, and perhaps of life itself.

In science, we often make progress by taking big problems and breaking them into smaller pieces. This strategy works fine for physics and engineering. But what are the significant informational units of neural and behavioral function? In the late 1970s and early 1980s, my students and I produced empirical evidence for a candidate called a coordinative structure [42] [43]. Coordinative structures are functional linkages among structural elements that are temporarily constrained to act as a single coherent unit. They are not (or at least, not only as we now know) hardwired and fixed in the way we tend to think of neural circuits; they are context dependent.⁴ Coordinative structures are softly assembled: all the parts are weakly interacting and interdependent. Perturbing them in one place produces remote compensatory effects somewhere else without disrupting, indeed preserving, functional integrity (for the history and evidence behind this proposal, see [11] [17, 44] [45]). Although beyond the scope of this chapter, a strong case can be made that coordinative structures – structural or functional effects produced by combining different elements – are units of selection in evolution [46] [47] and intentional change [48] [49]. Coordinative structures are the embodiment of the principle of functional equivalence: they handle the tremendous degeneracy of living things, using different parameter settings, combinations of elements, and recruiting new pathways “on the fly” to produce the same outcome [4].

Just as new states of matter form when atoms and molecules form collective behavior, is it possible that new states of biological function emerge when large ensembles of different elements form a coordinative structure? In other words, is the problem of coordination in living things continuous with cooperative and critical phenomena in open, nonequilibrium systems? The hexagonal forms produced in Bénard convection, the transition from incoherent to coherent light in lasers, the oscillating waves seen in chemical reactions, the hypercycles characteristic of catalytic processes, and so on are all beautiful examples of pattern generation in nature [50]. Such systems organize themselves: the key to their understanding lies in identifying the necessary and sufficient conditions for such self-organization to occur. Strictly speaking, there is no “program” inside the system that represents or prescribes the pattern before it appears or changes. This is not to say that very special boundary conditions do not exist in neurobehavioral coordination, intention among them [11] [51].

4.4 Beyond Analogy

As Weyl did, we start out with a vague idea. The vague idea or intuition is that biological coordination is fundamentally a self-organizing dynamical process. As nonequilibrium phase transitions lie at the heart of self-organization in many of nature's pattern-forming systems, this means it should be possible to demonstrate that they exist in biological coordination. To prove they exist, however, all the hallmark features of nonequilibrium phase transitions should be observable and quantifiable in biological coordination at behavioral and neural levels. But as Weyl says, for this approach to work, we need a specific case. That means specific experiments and specific theoretical modeling.

Ideally, one would like to have a simple model system that affords the analysis of pattern formation and pattern change, both in terms of experimental data and theoretical tools. Rhythmic finger movements are a potentially good model system because they can be studied in detail at both behavioral and brain levels. An experimental advantage is that rhythmic movements, although variable and capable of adjusting to circumstances, are highly reproducible. If I ask you to voluntarily move your finger back and forth as if you were going to do it all day, the variability in periodicity would be about 2–4% of the period you choose. Moreover, an extensive and informative literature on rhythmical behavior exists in neurobiological systems in vertebrates and invertebrates [52–60], the brain [61–64], and biological clocks in general [65]. Rhythmic behavior in living things is produced by a diversity of mechanisms. The goal here – by analogy to the theory of phase transitions – is to understand how all these different mechanisms might follow the same basic rules. To go beyond metaphor and analogy, we need an experimental window into biological coordination that might allow us to transcend different systems and reveal the operation of higher order principles. Could it be that bimanual rhythmic finger (or hand) movements in humans might be akin to the dynamically stable gaits of creatures and that “gait switching” might be similar to a nonequilibrium phase transition indicative of self-organizing processes? But, of course, an aim of science is to move from analogy to reality, from “this is like that” to “what is.”

4.5 An Elementary Coordinative Structure: Bimanual Coordination

Much of the early central pattern generator (CPG) literature was based on creatures doing one thing, such as flying, swimming, feeding, or walking (e.g., [66] [53]). Yet, in addition to being degenerate, different anatomical combinations capable of accomplishing the same outcome, coordinative structures are also multifunctional: they often use the same anatomical components to accomplish different functions. What was needed was to invent an experimental model system that affords looking at how people do more than one thing under the same conditions. One of the early ways we used to identify coordinative structures in perceptuomotor behavior was to seek invariants under transformation. More simply, to see if despite many variations, for example, in the activity of neurons, muscles, and joints, some quantities are preserved, while other variables, such as the forces that have to be generated to accomplish a given task, are altered. We used this strategy to uncover a coordinative structure in studies of discrete interlimb coordination: we found, in these experiments on voluntary movement, that the brain does not coordinate the limbs independently but rather preserves their relative timing by means of functional linkages – neurons, joints, and muscles are constrained to act as a single unit [42]. The same seems to hold in speech [67]. Even earlier work, by ourselves and others [68–70] was suggestive that discrete movements are equilibrium seeking; they exhibit equifinality regardless of initial conditions very much as a (nonlinear) mass spring system oscillates or not depending on parameters [71].⁵ Ironically enough, given the apparent significance of rhythms and synchronization in the brain [61] [72, 73], the nonlinear oscillator was viewed as the most elementary form of a coordinative structure [71] [74, 75].

In the original experiments, subjects were tasked to rhythmically move their index fingers back and forth in one of two patterns (in-phase or antiphase). In the former pattern, homologous muscles contract simultaneously; in the latter, the muscles contract in an alternating manner. In various experiments, subjects either just increased frequency voluntarily or a pacing metronome was used, the frequency of which was systematically changed from 1.25 to 3.50 Hz in 0.25 Hz steps [79] [80]. What was discovered was that when subjects began in the antiphase pattern, at a certain frequency or movement rate they spontaneously shifted into the in-phase pattern. On the other hand, if the subject started at a high or low rate with an in-phase movement and the rate was slowed down or sped up, no such transition occurred. Of further note was that although the transitions occurred at different rates of finger or hand motion for different subjects, and were lowered when subjects did the same experiment under resistive loading conditions, when the critical transition frequency was scaled to the subject's preferred frequency and expressed as a ratio (by analogy to the reduced temperature in the phase transitions described earlier), the resulting dimensionless number was constant. Moreover, invariably, the relative phase fluctuated before the transition and – despite the fact that subjects were moving faster – these fluctuations decreased after the switch. Many experimental studies of bimanual rhythmic movements demonstrate that humans – without prior learning [81] [82] – are able to stably produce two patterns of coordination at low frequency values, but only one – the symmetrical, in-phase mode – as frequency is scaled beyond a critical value. This is a remarkable result given the complexity of the nervous system, the body, and their interaction with the world.⁶

4.6 Theoretical Modeling: Symmetry and Phase Transitions

In order to understand the patterns of coordination observed and the changes they undergo in terms of dynamics, we need to address the following questions: first, what are the essential variables (order parameters) and how is their dynamics to be characterized? Second, what are the control parameters that move the system through its collective states? Third, what are the subsystems and the nature of the interactions that give rise to such collective effects? Fourth, can we formulate a theoretical model, and if so what new experimental observations does the theoretical model predict?

In a first step, the relative phase, ø may be considered a suitable collective variable that can serve as an order parameter. The reasons are as follows: (i) ø characterizes the patterns of spatiotemporal order observed, in-phase and antiphase; (ii) ø changes far more slowly than the variables that describe the individual coordinating components (e.g., position, velocity, acceleration, electromyographic activity of contracting muscles, neuronal ensemble activity in particular brain regions, etc.); (iii) ø changes abruptly at the transition and is only weakly dependent on parameters outside the transition; and (iv) ø has simple dynamics in which the ordered phase relations may be characterized as attractors. As the prescribed frequency of oscillation, manipulated during the experiment, is followed very closely, frequency does not appear to be system dependent and therefore qualifies as a control parameter.

Determining the coordination dynamics means mapping observed, reproducible patterns of behavior onto attractors of the dynamics. Symmetry may be used to classify patterns and restrict the functional form of the coordination dynamics. Symmetry means “no change as a result of change”: pattern symmetry means a given pattern is symmetric under a group of transformations. A transformation is an operation that maps one pattern onto another, for example, left–right transformation exchanges homologous limbs within a bimanual pattern. If all relative phases are equivalent after the transformation, then the pattern is considered invariant under this operation. Symmetry serves two purposes. First, it is a pattern classification tool allowing for the identification of basic coordination patterns that can be captured theoretically. Given a symmetry group, one can determine all invariant patterns. Second, imposing symmetry restrictions on the dynamics itself limits possible solutions and allows one to arrive at a dynamics that contains the patterns as different coordinated states of the same nonlinear dynamical system (see also [84]). In other words, basic coordination patterns correspond to attractors of the relative phase for certain control parameter values. Left–right symmetry of homologous limbs leads to invariance under the transformation ø → ø, so that the simplest dynamical system that accommodates the experimental observations is:

4.1

where φ is the relative phase between the movements of the two hands, 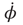is the derivative of φ with respect to time, and the ratio b/a is a control parameter corresponding to the movement rate in the experiment. An equivalent formulation of Eq. (4.2) is:

4.2

Using a scaling procedure commonly employed in the theory of nonlinear differential equations, Eqs. ((4.1)) and (4.2) can be written with only a single control parameter k = b/a in the form

4.3

In the literature, Eqs. ((4.1)–4.3) are known as the HKB model after Haken, Kelso, and Bunz, first published in 1985 [85]. An attractive feature of HKB is that when visualized as a phase portrait or a potential function⁷ (Figure 4.2), it allows one to develop an intuitive understanding of what is going on in the experiments. It also facilitates the connection (which should not be assumed) between the key concepts of stability and criticality and the observed experimental facts. Just as the coupling among spins, K in Wilson's model of ferromagnetism varies with temperature, so the coupling among the fingers k = b/a in the HKB formulation varies with movement frequency/rate in the Kelso [79] [80] experiments. In Figure 4.2 a large value of k corresponds to a slow rate, whereas k close to zero indicates that the movement rate is high.

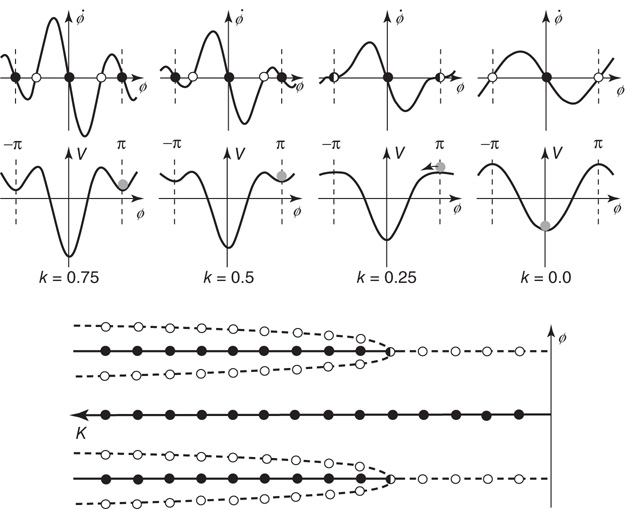
Figure 4.2 Dynamics of the basic HKB model as a function of the control parameter k = b/a. Top row: Phase flows of 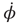(the derivative of φ with respect to time) as a function of φ. Stable and unstable fixed points are filled and open circles respectively (Eq. (4.3)). Middle: Landscapes of the potential function V(φ). Note the movement of the gray ball as the landscape deforms due to control parameter changes. Bottom: Bifurcation diagram, where solid lines with filled circles correspond to attractors and dashed lines with open circles denote repellors. Note that k decreases from to left (k = 0.75, bistable) to right (k = 0, monostable).

In the phase space plots (Figure 4.2 top row) for k = 0.75 and 0.5, there exist two stable fixed points at ø = 0 and π (rad) where the function crosses the horizontal axis (derivative of ø with respect to time goes to zero with a negative slope), marked by solid circles (the fixed point at −π is the same as the fixed point at π as the function is 2π-periodic). These attractors are separated by repellors, zero crossings with a positive slope, and marked by open circles. For movement rates corresponding to these two values of k, HKB shows that both antiphase and in-phase are stable. When the rate is increased, corresponding to a decrease in the coupling or control parameter k to the critical point at k_c = 0.25, the former stable fixed point at ø = π collides with the unstable fixed point and becomes neutrally stable as indicated by a half-filled circle. Beyond k_c, that is, for faster rates and smaller values of k, the antiphase pattern is unstable and the only remaining stable coordination pattern is in-phase.

The potential functions, shown in the second row in Figure 4.2, contain the same information as the phase portraits: they are just a different representation of the coordination dynamics. However, the strong hysteresis (a primitive form of memory) is more intuitive in the potential landscape than in phase space, and is best seen by mapping experimental data in which slow movements start out in an antiphase mode (the gray ball in the minimum of the potential at ø = π) and rate is increased. After passing the critical value of k_c = 0.25, the slightest perturbation puts the ball on the downhill slope and initiates a switch to in-phase. If the movement is now slowed down again, going from right to left in the plots, even though the minimum at ø = π reappears, the ball cannot jump up and populate it again but stays in the deep minimum at ø = 0.

Finally, a bifurcation diagram is shown at the bottom of Figure 4.2. The locations of stable fixed points for the relative phase ø are plotted as solid lines with solid circles and unstable fixed points as dashed lines with open circles. Around k_c = 0.25, the system undergoes a subcritical pitchfork bifurcation. Note that the control parameter k in this plot increases from right to left. Evidently, the HKB coordination dynamics represented by Eqs. ((4.1)–4.3), is capable of reproducing all the basic experimental findings listed earlier. From the viewpoint of theory, this is a necessary criterion for a model that has to be fulfilled but it is not sufficient. More important is whether the theoretical model predicts novel effects that can be tested experimentally. This is where we see the full power of the theory of nonequilibrium phase transitions, predicted hallmarks of critical phenomena, and self-organization in biological coordination. (The reader may rightfully ask about the subsystems, the individual components, and how they are coupled. This is a major feature of HKB [85] and has been addressed in detail both experimentally and theoretically but we will not consider it further here, see, e.g., [15] [86, 89], for recent reviews.)

A chief strategy of HKB is to map the reproducibly observed patterns onto attractors of a dynamical system. (In practical terms, we use transitions to define what the coordination states actually are, i.e., to separate the relevant from the irrelevant variables.) Thus, stability is a central concept, not only as a characterization of the two attractor states but also because (if biological coordination is really self-organized) it is loss of stability that plays a critical role in effecting the transition. Stability can be measured in several ways: (i) if a small perturbation drives the system away from its stationary state, the time it takes to return to a stationary state is independent of the size of the perturbation (as long as the latter is small). The “local relaxation time,” τ_rel, (i.e., local with respect to the attractor) is therefore an observable system property that measures the stability of the attractor state. The smaller τ_rel is, the more stable is the attractor. The case τ_rel → ∞ corresponds to a loss of stability. (ii) A second measure of stability is related to noise sources. Any real system is composed of and coupled to, many subsystems. (Think of the number of neurons necessary to activate a purposeful movement of a single finger, never mind playing the piano.) Random fluctuations exist in all systems that dissipate energy. In fact, there exists a famous theorem that goes back to Einstein, known as the fluctuation–dissipation theorem, which states that the amount of random fluctuations is proportional to the dissipation of energy in a system. The importance of this theorem for a wide class of nonequilibrium states and irreversible processes in general has been recognized for a long time. It is an explicit statement of the general relationship between the response of a given system to an external disturbance and the internal fluctuations of the system in the absence of the disturbance (see, e.g., [90]).

In our case, fluctuations may be seen to act to a certain degree as stochastic forces on the order parameter, relative phase. The presence of stochastic forces and hence of fluctuations of the macroscopic variables, is not merely a technical issue, but of both fundamental and functional importance. In the present context, stochastic forces act as continuously applied perturbations and therefore produce deviations from the attractor state. The size of these fluctuations as measured, for example, by the variance or standard deviation (SD) of φ around the attractor state, is a metric of its stability. Stability and biological variability are two sides of the same coin. The more stable the attractor, the smaller the mean deviation from the attractor state for a given strength of fluctuations.

4.7 Predicted Signatures of Critical Phenomena in Biological Coordination

4.7.1 Critical Slowing Down

Critical slowing down corresponds to the time it takes the system to recover from a small perturbation Δ. In Figure 4.3 (bottom), as long as the coupling k corresponding to the experimental movement rate is larger than k_c, the effect of a small perturbation will decay in time. However, as the system approaches the critical point, this decay will take longer and longer. At the critical parameter value, the system will not return to the formerly stable state: it will even move away from it. Direct evidence of critical slowing down was obtained originally from perturbation experiments that involved perturbing one of the index fingers with a brief torque pulse (50 ms duration) as subjects performed in the two natural coordinative modes. Again, frequency was used as a control parameter, increasing in nine steps of 0.2 Hz every 10 s beginning at 1.0 Hz. Again, when subjects began in the antiphase mode, a transition invariably occurred to the in-phase mode, but not vice versa. Relaxation time was defined as the time from the offset of the perturbation until the continuous relative phase returned to its previous steady state. As the critical frequency was approached, the relaxation time was found to increase monotonically – and to drop, of course, when the subject switched into the in-phase mode [91]. Using another measure of relaxation time, the inverse of the line width of the power spectrum of relative phase [92], strong enhancement of relaxation time, was clearly observed.

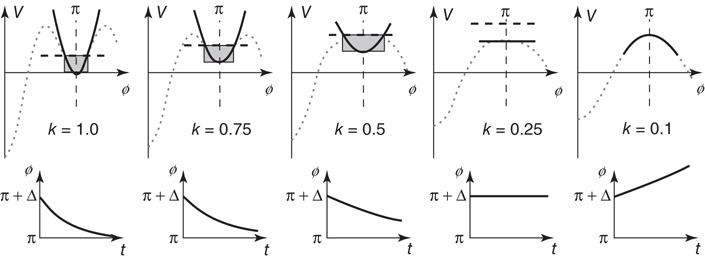
Figure 4.3 Hallmarks of a nonequilibrium (HKB) system, approaching criticality under the influence of a control parameter, k corresponding to the coupling between the fingers and directly related to the frequency of movement in experiments. Enhancement of fluctuations is indicated by the widening shaded area; critical slowing down is shown by the time it takes for the system to recover from a perturbation (bottom); critical fluctuations occur where the top of the shaded area is higher than the closest maximum in the potential, initiating a switch even though the system may still be stable.

4.7.2 Enhancement of Fluctuations

Fluctuations are sources of variability that exist in all dissipative systems. They kick the system away from the minimum and (on average) to a certain elevation in the potential landscape, indicated by the shaded areas in Figure 4.3. For large values of k, the horizontal extent of this area is small but becomes larger and larger when the transition point is approached. The SD of the relative phase is a direct measure of such fluctuation enhancement and is predicted to increase when the control parameter approaches a critical point. Even cursory examination of typical experimental trajectories in the original experiments revealed the presence of fluctuations (e.g., [80]). As the control parameter frequency was increased in the antiphase mode, relative phase plots became increasingly variable near the transition and were slower to return from deviations. Follow-up experiments designed to test the specific prediction of nonequilibrium phase transitions clearly demonstrated the existence of fluctuation enhancement before the transition ([93]; see also [94]).

4.7.3 Critical Fluctuations

Even before it reaches the critical point, fluctuations may kick the system into a new mode of behavior. In Figure 4.3, if fluctuations reach a height higher than the closest maximum – the hump that has to be crossed – a transition will occur, even though the fixed point is still classified as stable. Again, this often happens in experiments (e.g., [95]).

All these hallmarks of critical phenomena can be (and have been) treated in a quantitative manner by adding a stochastic term Q to Eq. (4.3) and treating the coordination dynamics as a Langevin equation with both a deterministic and a stochastic aspect

4.4

with

In this case, the system is no longer described by a single time series but by a probability distribution that evolves in time. Such time-dependent processes are given by the corresponding Fokker–Planck equation. Using experimental information on the local relaxation times and the SD in the noncritical régime of the bimanual system, all model parameters a, b in Eq. (4.2) and the stochastic term Q were determined ([96] [97], Chapter 11 for details; see also [98]). In the critical régime, the full Fokker–Planck equation was solved numerically: without any parameter adjustment, the stochastic version of HKB accounted for all the transient behavior seen experimentally. That is, quantitative measures of enhancement of fluctuations, critical fluctuations, and critical slowing down in a biological system were accounted for both qualitatively and quantitatively by a straightforward extension of the HKB model. Moreover, attesting further to the interplay between theory and experiment, new aspects were predicted such as the duration of the transient from the antiphase to the in-phase state – which we called the switching time. The basic idea is that during the transition, the probability density of relative phase – initially concentrated around φ = π flows to φ = 0 and accumulates there. In this case, it is easy to calculate the time between the relative phase immediately before the transition and the value assumed immediately after the transition. The match between theoretically predicted and empirically observed switching time distributions was impressive, to say the least [92] [94]. This aspect is particularly interesting, because it shows that the switching process itself is closely captured by a specific model of stochastic nonlinear HKB dynamics.

4.8 Some Comments on Criticality, Timescales, and Related Aspects

In the HKB system (Eq. (4.4)), as the transition is approached (i.e., the antiphase mode loses its stability), the local relaxation time (with respect to the antiphase mode) increases, while the global relaxation time decreases (because the potential hill between 0° and 180° vanishes). At the critical point, both are of the same order as the observed time and one can see the transition. Thus, at the transition point, the time scales relation breaks down, and an additional timescale assumes importance, namely, the time scale of parameter change, τ_p. This reflects the fact (as occurs often in biological systems and nearly all experiments) that the control parameter that brings about the instability is itself changed in time. The relation of the time scale of parameter change to other system times (local relaxation times, global equilibration time, etc.) plays a decisive role in predicting the nature of the phase transition. If the system changes only as the old state becomes unstable, transition behavior is referred to as a second-order phase transition (because of an analogy with equilibrium phase transitions, see, e.g., [99]). In that case, features of critical phenomena (such as critical fluctuations and critical slowing down) are predicted. If, on the other hand, the system, with overwhelming probability, always seeks out the lowest potential minimum, it may switch before the old state becomes unstable. Jumps and hysteresis (among other features) are generally predicted. This behavior is called a first-order phase transition. Notice that the origin of critical phenomena in the present case is different from equilibrium phase transitions. In particular, in the original HKB model symmetry breaking does not occur, but rather a breakdown of timescales relations.⁸ In real experiments, timescale relations have to be considered.

The main conclusion to be drawn from this empirical and theoretical work is that it demonstrates – in both experimental data and theoretical modeling – predicted features of nonequilibrium phase transitions in human behavior. Nonequilibrium phase transitions are the most fundamental form of self-organization that Nature uses to create spatial, temporal (and now functional) patterns in open systems. Fluctuations and variability play a crucial role, testing whether a given pattern is stable, allowing the system to adapt and discover new patterns that fit current circumstances. The notion – dominant in those days – that movements are controlled and coordinated by a “motor program” is brought into question. Critical fluctuations, for instance, although typical of nonequilibrium phase transitions, are problematic for stored programs in a computer-like brain.

Currently, it is quite common for investigators to take a time series from some task such as tapping or drawing a circle or reacting to stimuli or balancing a pole for a long period of time and to describe its variability using, for example, detrended fluctuation analysis to assess long-range correlations. Basically, long-range correlations refer to the presence of positive autocorrelations that remain substantially high over large time lags, so that the autocorrelation function of the series exhibits a slow asymptotic decay, never quite reaching zero. Basic physiological functions such as walking and heart beats and neural activity have also been examined. Such analyses are useful, even important, for example, for heartbeat monitoring and other dynamic diseases or for distinguishing human performance in different task conditions over the long term (e.g., [100–103]) – or even individual differences between people in performing such tasks. One should be conscious, however, of the ancient saying attributed to Heraclitus; “no man ever steps in the same river twice, for it's not the same river and he's not the same man.” There are reasons to be cautious about taking a single time series, calculating its statistical properties such as long-range correlations and concluding that the latter arise as a universal statistical property of complex systems with multiple interdependent components ranging from the microscopic to the macroscopic that are, as it were, allowed to fluctuate on their own (see also [104] for measured, yet positive criticism). This looks too much like science for free, rather like the way calculations of correlation dimension from time series were pursued in the 1980s and 1990s. With respect to individual differences, for example, it would seem more important to identify preferences, dispositions, and biases in a given context so that one may know what can be modified and the factors that determine the nature of change [81].

Criticality and phase transitions can be used in a constructive manner, as a way to separate the relevant variables and parameters from the irrelevant ones – and as a means of identifying dynamical mechanisms of pattern formation and change in biological coordination. As mentioned previously, in neuroscience, as well as the cognitive, behavioral, and social sciences, neither the key coordination quantities nor the coordination dynamics are known a priori. Criticality and instability can be used to identify them. Brain structure–function appears to be both hierarchically (top to down and bottom to up) as well as heterarchically (side to side) organized (e.g., [105]); the component elements and their interactions are heterogeneous (e.g., [106]); and the relevant coordination variables characterizing ongoing neural and cognitive processes are invariably dependent on context, task or function [11] [107].

4.9 Symmetry Breaking and Metastability

Notice that the HKB Eqs. ((4.1)–4.4) are symmetric: the elementary coordination dynamics is 2π periodic and is identical under left–right reflection (φ is the same as −φ). This assumes that the individual components are identical, which is seldom, if ever the case. Nature thrives on broken symmetry. To accommodate this fact, Kelso et al. [108] incorporated a symmetry-breaking term δω into the dynamics

4.5

for the equation of motion and the potential, respectively. The resulting coordination dynamics is now a function of the interplay between the coupling k = b/a and symmetry breaking. Small values of δω shift the attractive fixed points (Figure 4.4 middle) in an adaptive manner. For larger values of δω the attractors disappear entirely (e.g., moving left to right on the two bottom rows of Figure 4.4). Note, however, that the dynamics still retain some curvature: even though there are no attractors there is still attraction to where the attractors used to be (“ghosts” or “remnants”). The reason is that the difference (δω) between the individual components is sufficiently large and the coupling (k) sufficiently weak that the components tend to do their own thing, while still retaining a tendency to cooperate. This is the metastable régime of the CD.

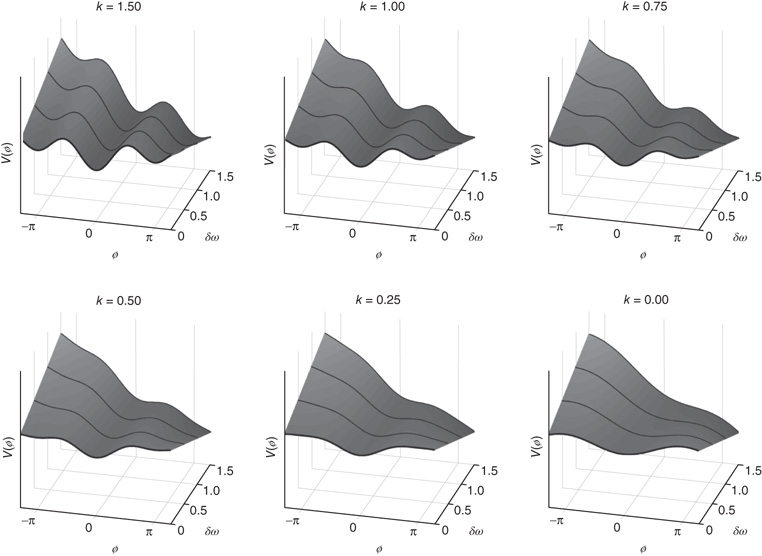
Figure 4.4 Potential landscapes of Eq. (4.5) as a function of symmetry breaking between the interacting components, δω and coupling, k = b/a (Eq. (4.5)). The bottom curve in each picture is the standard HKB model, that is, δω = 0. Remaining rows show how HKB is deformed because of the combination of coupling and symmetry-breaking parameters; as a consequence, entirely new phenomena are observed. The dynamical mechanism is a tangent or saddle-node bifurcation. Attractors shift, drift, and disappear with weaker coupling and larger differences (heterogeneity) between components. Note, however, that there is still attraction to where the attractors once were, “ghosts” or “remnants” indicated by slight curvature in the potential landscapes after minima disappear. This is the metastable régime of the elementary coordination dynamics, where coordination takes the form of coexisting tendencies for interaction and independence among the components.

The interplay of two simultaneously acting forces underlies metastability: an integrative tendency for the coordinating elements to couple together and a segregative tendency for the elements to express their individual autonomy ([11] [109]; see also [4] [23, 110] for most recent discussion of metastability's significance for brain and behavior).

A number of neuroscientists have embraced metastability as playing a key role in various cognitive functions, including consciousness (e.g., [111–119]; see [110] for review). Especially impressive is the work of Rabinovitch and colleagues, which ties metastable dynamics (robust transients among saddle nodes referred to as heteroclinic channels) to neurophysiological experiments on smell (e.g., [120]). The significance of metastability lies not in the word itself but in what it means for understanding coordination in the brain and its complementary relation to the mind [4] [23]. In CD, metastability is not a concept or an idea, but a product of the broken symmetry of a system of (nonlinearly) coupled (nonlinear) oscillations. The latter design is motivated by empirical evidence that the coordinative structures of the brain that support sensory, motor, affective, and cognitive processes express themselves as oscillations with well-defined spectral properties. At least 12 different rhythms from the infraslow (less than 1 Hz) to the ultrafast (more than 100 Hz) have been identified, all connected to various behavioral and cognitive functions (e.g., [121–123]). Indeed, brain oscillations are considered to be one of the most important phenotypes for studying the genetics of complex (non-Mendelian) disorders [124]. The mechanisms that give rise to rhythms and synchrony exist on different levels of organization: single neurons oscillate because of voltage-gated ion channels depolarizing and hyperpolarizing the membrane; network oscillations, for example, in the hippocampus and neocortex strongly depend on the activity of inhibitory GABAergic interneurons in the central nervous system (so-called inhibition-based rhythms, see, e.g., [125]); neuronal groups or assemblies form as transient coalitions of discharging neurons with mutual interaction. Neuronal communication occurs by means of synapses and glia (e.g., [126]). Synaptic connections between areas may be weak but research shows that synchrony among different inputs strengthens them, thereby enhancing communication between neurons (for one of the many recent examples, see [127]). Phase coupling, for example, allows groups of neurons in distant and disparate regions of the brain to synchronize together (e.g., [128] [129] for review). According to CD, nonlinear coupling among oscillatory processes and components that possess different intrinsic dynamics (broken symmetry) is necessary to generate the broad range of behaviors observed, including pattern formation, multistability, instability, metastability, phase transitions, switching (sans “switches”), hysteresis, and so forth. Although the mechanisms of coupling multiple oscillations within and between levels of organization are manifold, the principle is clear enough: dynamic patterns of brain behavior qua coordinative structures arise as an emergent consequence of self-organized interactions among neurons and neuronal populations. The said self-organization is a fundamental source of behavioral, cognitive, affective, and social function [11] [61, 72] [73, 130–133]. Transition behaviors are facilitated by dynamical mechanisms of criticality and metastability: the former reflects neural systems that tune themselves to be poised delicately between order and disorder [99] [134, 135]; the latter where there are no attractors in the nervous system but only the coexistence of segregative and integrative tendencies that give rise to robust metastable behavior – transient functional groupings and sequences [110] [136–138].

4.10 Nonequilibrium Phase Transitions in the Human Brain: MEG, EEG, and fMRI

In a long series of studies beginning in the late 1980s, my students, colleagues, and I used the nonlinear paradigm (varying a control parameter to identify transition-revealing collective variables or order parameters) as a means to find signature features of self-organizing nonequilibrium phase transitions in human brain activity recorded using large SQuID (e.g., [139–146]), and multielectrode arrays [88] [147–149] along with a variety of statistical measures of spatiotemporal (re)organization in the brain.

We and others followed this work up using functional magnetic resonance imaging (fMRI) to identify the neural circuitry involved in behavioral stability and instability (e.g., [150] [151]). We can mention just a couple of key findings here. First, a study by Meyer-Lindenberg et al. [152] demonstrated that a transition between bistable coordination patterns can be elicited in the human brain by transient transcranial magnetic stimulation (TMS). As predicted by the HKB model of coordination dynamics (Eq. (4.3)), TMS perturbations of relevant brain regions such as premotor and supplementary motor cortices caused a behavioral transition from the less stable antiphase state to the more stable in-phase state, but not vice versa. In other words, in the right context, that is, near criticality, tickling task-relevant parts of the brain at the right time caused behavior to switch.

CD theory predicts that cortical circuitry should be extremely sensitive to the dynamic stability and instability of behavioral patterns. If we did not know how behavioral patterns form and change in the first place, such predictions would be moot. Jantzen et al. [153] demonstrated a clear separation between the neural circuitry that is activated when a control parameter (rate) changes and those connected to a pattern's stability (see also [154]). As one might expect, activity in sensory and motor cortices increased linearly with rate, independent of coordination pattern. The key result, however, was that the activation of cortical regions supporting coordination (e.g., left and right ventral premotor cortex, insula, pre-SMA (supplementary motor area), and cerebellum) scaled directly with the stability of the coordination pattern. As the antiphase pattern became increasingly less stable and more variable, so too did the level of activation of these areas. Importantly, for identical control parameter values, the same brain regions did not change their activation at all for the more stable (less variable) in-phase pattern. Thus it is that these parts of the brain – which form a functional circuit – have to work significantly harder to hold coordination together. And thus it is that the difficulty of a task, often described in terms of “information processing load,” is captured by a dynamic measure of stability that is directly and lawfully related to the amount of energy used by the brain, measured by BOLD activity.

The Jantzen et al. [153] paper shows that different patterns of behavior are realized by the same cortical circuitry (multifunctionality). Earlier, it was shown that the same overt patterns of behavior [155] and cognitive performance [156] can be produced by different cortical circuitry (degeneracy). Together with the Meyer-Lindenberg et al. study, the Jantzen et al. [153] work demonstrates that dynamic stability and instability are major determinants of the recruitment and dissolution of brain networks, providing flexibility in response to control parameter changes (see also [157]). Multifunctionality qua multistability confers a tremendous selective advantage to the brain and to nervous systems in general: it means that the brain has multiple patterns at its disposal in its “restless state” and can switch among them to meet environmental or internal demands. Shifting among coexisting functional states whether through noise or exposure to changing conditions is potentially more efficient than having to create states de novo [4].

4.11 Neural Field Modeling of Multiple States and Phase Transitions in the Brain

Theoretical modeling work at the neural level [87] [158] has complemented experiments and theory at the behavioral level (see [21]). Neurobiologically grounded accounts based on known cellular and neural ensemble properties of the cerebral cortex (motivated by the original works of Wilson, Cowan, Ermentrout, Nunez, and others; see Chapter 22, this volume) have been proffered for both unimanual [141] [159–162] and bimanual coordination ([163]; see also [164–168]). In particular, the behavioral HKB equations were successfully derived from neural field equations, allowing for an interpretation of the phenomenological coupling terms [163]. An important step was to extend neural field theory to include the heterogeneous connectivity between neural ensembles in the cortex ([106] [169]; see also [170]). Once general laws at the behavioral and brain levels have been identified, it has proved possible to express them in terms of the excitatory and inhibitory dynamics of neural ensembles and their long- and short-range connectivities, thereby relating different levels of description ([171] [172]; see [21] and references therein for updates). In showing that stability and change of coordination at both behavioral and neural levels is due to quantifiable nonlinear interactions among interacting components – whether fingers or the neural populations that drive them – some of the mysticism behind the contemporary terms emergence and self-organization is removed. More important, this body of empirical and theoretical work reveals the human dynamic brain in action: phase transitions are described by the destabilization of a macroscopic activity pattern when neural populations are forced to reorganize their spatiotemporal behavior. Destabilization is typically controlled via unspecific scalar control parameters. In contrast, traditional neuroscience describes reorganization of neural activity as changes of spatial and timing relations among neural populations. Both views are tied together by our most recent formulation of neural field theory: here, the spatiotemporal evolution of neural activity is described by a nonlinear retarded integral equation, which has a heterogeneous integral kernel. The latter describes the connectivity of the neocortical sheet and incorporates both continuous properties of the neural network as well as discrete long-distance projections between neural populations. Mathematical analysis (e.g., [106]) of such heterogeneously connected systems shows that local changes in connectivity alter the timing relationships between neuronal populations. These changes enter the equations as a control parameter and can destabilize neural activity patterns globally, giving rise to macroscopic phase transitions. Heterogeneous connectivity also addresses the so-called stability–plasticity dilemma: stable transmission of directed activity flow may be achieved by projecting directly from area A to area B and from there to area C (stability). However, if necessary, area A may recruit neighboring populations of neurons (plasticity), as appears to be the case in bimanual coordination [88].

Reorganization of spatiotemporal neural activity may be controlled via local changes in the sigmoidal response curves of neural ensembles, the so-called conversion operations (see also [173] for an account based on synaptic depression). Conversion operations have been investigated in quantitative detail as a function of attention (e.g., [174]). The main result is that the slope and the height of the sigmoid vary by a factor of 2.5 between minimal and maximal attention. The sigmoidal variation of the ensemble response is realized biochemically by different concentrations of neuromodulators such as dopamine and norepinephrine. Mathematically, the neural dynamics described by the spatiotemporal integral equations can be coupled to a one-dimensional concentration field in which elevated values designate increased values of slope and height of the sigmoidal response curve of neural ensembles. An increased slope and height of the sigmoid typically causes increased amplitude and excitability of the neural sheet. It is known that novel (or more difficult) tasks require more attention/arousal than an automated behavioral pattern [175] [176]. Increased attention demand is realized in the cortical sheet via a larger concentration of the neurotransmitter, resulting in a steeper slope and elevation of the sigmoid response function. As a consequence, excitability and amplitude of neural activity are increased in task conditions, requiring more attention. During learning, changes in connectivity occur. After learning, the task condition is no longer novel, but rather more “automated,” reflected in decreased concentrations of neurotransmitters and thus decreased excitability and amplitude of ongoing neural activity (see also [175]). Notably, in all our experiments, spanning the range from magnetoencephalography (MEG) to fMRI BOLD measurements, neural activity in stability-dependent neural circuitry increases before and drops across the antiphase to in-phase transition, even though the system is moving faster – attesting further to the significance of dynamic stability and instability for functionally organized neural circuitry (coordinative structures) in the brain and behavior.

4.12 Transitions, Transients, Chimera, and Spatiotemporal Metastability

Here, we mention only a few further points that are relevant to critical behavior in humans and human brains. The first illustrates the power of Eq. (4.6) and the message of complex, nonlinear dynamical systems: where a system lives in parameter space dictates how it behaves. Figure 4.5 displays an array of transients and transitions found in simple experiments on social coordination in which pairs of subjects move their fingers at their own preferred frequency with and without the vision of the other's movements ([123] [132]; see also [133] [177]). Although a main goal, for example, of the Tognoli et al. [123] research was to identify neural signatures (“neuromarkers”) of effective, real-time coordination between people and its breakdown or absence, this is not the main point we wish to convey or of Figure 4.5. Each rectangular box in the figure shows the instantaneous period (in seconds) of each person's flexion–extension finger movements and the relative phase (in radians) between them in a single trial lasting 60 s.

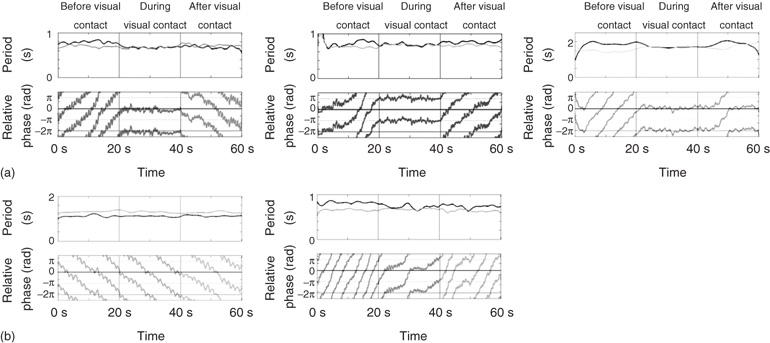
Figure 4.5 Spontaneous patterns of social coordination. Each pair of rectangular boxes shows the instantaneous period (above) and relative phase (below) of voluntary finger movements of each member of a social dyad over the course of a 60 s trial. In the first and last 20 s of each trial, subjects are prevented from seeing each other's movements. Vision is available only in the middle 20 s of the trial (see text and [123] for details). (a) Different kinds of disorder-to-order and order-to-disorder transitions before and after vision of the other's movements are shown. (b) (Left) Shown here is a kind of “social neglect”: subjects do not spontaneously coordinate when they see each other's movements. They continue to move at their self-chosen frequency and the relative phase wraps continuously throughout the trial. (Right) Transient but robust metastable behavior is revealed during visual coupling. Disorder (phase-wrapping) transitions shift toward in-phase and drifting behavior during visual information exchange.

Throughout each trial, subjects were simply asked to adopt a frequency or rate of movement that they felt most comfortable “as if you can do it all day.” The vertical lines in each box correspond to the three manipulations or phases in every trial of the experiment; each phase lasts 20 s. In the first 20 s, subjects were prevented from seeing each other's finger movements by means of an opaque liquid crystal (LC) screen. Then, in the next 20 s, the LC screen became transparent so that subjects could see each other's movements. In the last 20 s, the LC screen became opaque, again preventing vision of the other. The top row of boxes (a) illustrate disorder (measured as phase wrapping) to order (in-phase, left and right; antiphase, middle) transitions and vice-versa. Notice the effect of current conditions on whether disorder to order transitions are toward in-phase or antiphase coordination; the relative phase just before the LC screen becomes transparent (i.e., neither member of the pair has vision of the other's movements) dictates the nature of the transition process. If the relative phase is wrapping near in-phase (Figure 4.5a, left and right) or antiphase when subjects suddenly see each other's movements, transitions occur to the nearest dynamically stable state. Notice also that in the top right part of the figure, the relative phase lingers at in-phase even though subjects are no longer visually coupled – a kind of “social memory” or remnant of the interaction is observed before subjects' movement periods diverge. Many interesting questions may be raised about this paradigm: who leads, who follows, who cooperates, who competes, who controls, and why. For now, the point is that all these states of coordination, disorder, transients, and transitions fall out of a path (itself likely idiosyncratic and time dependent) through the parameter space of the extended, symmetry-breaking HKB landscapes shown in Figure 4.4 (see also Figure 4e in [4]). Interestingly, many of the same patterns have been observed when a human interacts with a surrogate or avatar driven by a computationally implemented model of the HKB equations, a scaled-up, fully parameterizable human dynamic clamp akin to the dynamic clamp of cellular neuroscience [178] [179].

Even more exotic kinds of criticality and coexistence states can be observed in simple forms of biological coordination – although they have taken their time to see the light of day. Consider the Kelso [80] experiments in which subjects are instructed to coordinate both left and right finger movements with the onset of a flash of light emitted periodically by a diode placed in front of them or by an auditory metronome. Sensory input from visual or auditory pacing stimuli are used as a control parameter to drive the system beyond criticality to discover new coordination states (see also [180]). Hearkening back to Bohr's [181] use of the word phenomenon, that is, “to refer exclusively to observations obtained under specified circumstances, including an account of the whole experiment,” one can see that a closer look at this experimental arrangement affords a unique possibility to study the interplay of the coupling between the two hands and the coupling between each hand and environmental stimuli. This makes for three kinds of interactions. “The whole experiment” contains a combination of symmetry (left and right hands), symmetry breaking (fingers with visual pacing stimulus), and different forms of coupling (proprioceptive-motor and visuomotor). Figure 4.6 shows an example of behavioral data from a more recent study that used the Kelso paradigm for a different purpose, namely, to examine how spatiotemporal brain activity was reorganized at transitions [88].

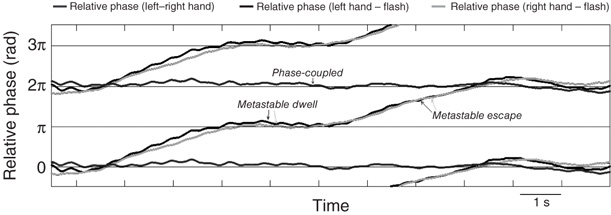
Figure 4.6 Evidence for a “chimera” in visuomotor coordination: the coexistence of phase coupling (between the left and right index fingers) and metastability (dwell and escape) between each finger and visual pacing stimuli.

The data shown in Figure 4.6 suggest that the coupling between the left and right hands is stronger than the coupling between hands and rhythmic visual stimuli. At high frequency, that is, after the usual transition from antiphase to in-phase coordination has occurred, a mixed CD composed of phase coupling and metastability is observed. That is, left and right finger movements are in-phase, and at the same time, the relative phase between the fingers and visual stimuli exhibits bistable attracting tendencies, alternating near in-phase and near antiphase. This is the empirical footprint of the emergence of a so-called chimera dynamics – named after the mythological creature composed of a lion's head, a goat's body, and a serpent's tail [182–184]. The key point is that two seemingly incompatible kinds of behavior (phase locking and metastability) coexist in the same system and appear to arise due to nonlocal coupling.⁹ Although so-called chimera are a relatively new area of empirical and theoretical research, the data presented in Figure 4.6 clearly show that both stable and metastable dynamics are part and parcel of the basic repertoire of human sensorimotor behavior. The paradigm allows for the study of integrative and segregative tendencies at the same time – an important methodological and conceptual advantage when it comes to understanding the spatiotemporal (re)organization of brain activity [185] [186].

4.13 The Middle Way: Mesoscopic Protectorates

In the past 30 years or so, principles of self-organizing dynamical systems have been elaborated and shown to govern patterns of coordination (i) within a moving limb and between moving limbs; (ii) between the articulators during speech production; (iii) between limb movements and tactile, visual, and auditory stimuli; (iv) between people interacting with each other spontaneously or intentionally; (v) between humans and avatars; (vi) between humans and other species, as in riding a horse; and (vii) within and between the neural substrates and circuitry that underlie the dynamic brain in action, as measured using MEG, electroencephalography (EEG), and fMRI ([8] [16, 17] [21] for reviews). There are strong hints that laws of coordination in neurobehavioral dynamical systems such as HKB and its extensions are universal and deal with collective properties that emerge from microscopic dynamics. Phase transitions are the core of self-organization. Since their original discovery in experiments and consequent theoretical modeling, phase transitions and related dynamical phenomena have been observed in many different systems at different levels of description ranging from bimanual and sensorimotor coordination and their neural correlates, to interpersonal and interbrain coordination (for reviews, see [15–17] [173, 187–189]). The bidirectional nature of the coupling proves to be a crucial aspect of dynamic coordination, regardless of whether hands, people, and brains are interacting for social functions [21] or astrocytes and neurons are interacting through calcium waves for normal synaptic transmission [34].

Although in some cases, akin to HKB and more recent extensions such as the Jirsa–Kelso Excitator model of discrete and continuous behavior [89] [190–192], it has proved possible to derive the order parameter dynamics at one level from the nonlinear components and their nonlinear interaction (e.g., in HKB using the well-known rotating wave and slowly varying amplitude approximations of nonlinear oscillator theory), in general it is not possible to deduce higher level descriptions from lower level ones. Laughlin and Pines [193] present a broad range of emergent phenomena in physics that are regulated by higher organizing principles and are entirely insensitive to microscopic details. The crystalline state, they remark, is the simplest known example of what they call a quantum “protectorate,” a stable state of matter whose low-energy properties are determined by a higher organizing principle and nothing else. More is different, to use Anderson's [194] apt phrase. Self-organization is not inherently quantum mechanical, but has more to do with hierarchies and separation of time scales (mathematically, the center manifold and/or the inertial manifold where slow time scale processes tend to dominate faster ones, cf. [50] [195]). In recognizing emergent rules, physics has given up reductionism for the most part, although biology still clings to it. In the spirit of the complementary nature [11] [196, 197], both are important, perhaps for different reasons.

So-called laws of coordination (e.g., [9] [45, 198] [199]) – CD – some of the basic ones of which are described briefly here, correspond to emergent rules of pattern formation and change that cut across different systems, levels, and processes. They contain universal features such as symmetry, symmetry breaking, multistability, bifurcations, criticality, phase transitions, metastability, and chimera. They are likely candidates for Laughlin and Pines's “protectorates”: generic, emergent behaviors that are reliably the same from one system to another regardless of details and repeatable within a system on multiple levels and scales [45]. If laws of coordination are truly emergent and sui generis as they seem to be, it may not be possible – even in principle – to deduce, say, psychological-level descriptions from (more microscopic) neural- or molecular-level descriptions. This does not mean that we should not try to understand the relationships between different levels. Rather, the task of CD is to come up with lawful descriptions that allow us to understand emergent behavior at all levels and to respect the (near) autonomy of each. Evidence suggests that one of CD's most elementary forms – the extended HKB model with its subtle blend of broken symmetry and informationally based coupling – constitutes an intermediate level, a middle ground, or “mesoscopic protectorate” that emerges from nonlinear interaction among context-dependent components from below and boundary conditions from above [11].

4.14 Concluding Remarks

We have reviewed empirical and theoretical evidence showing that criticality is a prominent aspect of the brain and what brains do. All the predictions of nonequilibrium phase transitions have been observed and modeled, indicating that dynamic patterns of human behavioral and brain activity emerge fundamentally as cooperative phenomena in complex, nonlinear dynamical systems. After 70-odd years of “circuit breaking” in invertebrates and vertebrates, plus many conceptual and empirical developments, it appears that the notion of circuit – forced by data – is an unlikely metaphor for the way the cerebral cortex works. Once you “free the creature up” and take into account behavior, multifunctionality, indeterminacy, and degeneracy are the organism's modus operandi. Many years of brilliant research on central pattern generators (note the noun form) has led to the need for a more flexible and dynamical construct to account for behavior. Neural circuits of structurally connected context-independent parts responsible for particular functions are more likely the exception than the rule. Multifunctional, context-dependent neural circuitry with recruitment capabilities and a context-dependent “parts list” seems closer to reality. In this respect, the work of Prinz et al. [84] is illuminating. Following the common assumption that neural circuits must be regulated in a highly specific manner to function properly, Prinz et al. simulated the pyloric network of the crustacean stomatogastric ganglion using different combinations of synaptic strengths and neuron properties. In over 20 million versions of a three-cell model, they showed that virtually indistinguishable network activity can arise from widely disparate sets of underlying mechanisms. Many different combinations of synaptic strengths and intrinsic membrane properties were found to be capable of producing the same outcome. Likewise, as shown here as a natural aspect of CD, for example, in the symmetry-breaking version of HKB, many different combinations of coupling (k) and intrinsic parameters (δω) produce the same outcome: degeneracy and functional equivalence in spades. In addition, at critical values of parameters abrupt change happens – a different outcome emerges.

As CD has shown, nonlinearity is essential for biological functions such as switching, decision making, pattern selection, and stabilization. Here, we proposed a flexible yet stable concept of behavioral and neural function that accommodates the degeneracy and multifunctionality of biological things or processes. Unlike fixed circuitry, coordinative structures in the nervous system are softly assembled; all the parts are context dependent and weakly interacting. Perturbing one part may produce a remote effect somewhere else without disrupting (indeed preserving) integrity of function. Coordinative structures have been shown to form and change by means of nonequilibrium phase transitions, a basic self-organizing mechanism for spontaneous pattern formation and change in natural systems. The dynamics of coordinative structures is plastic yet stable; change may be sudden or gradual, and persist or not. The (essentially nonlinear) dynamics determines not only which new patterns are formed but also their sustainability, that is, which patterns persist following smooth or abrupt change. Analysis shows that the spatiotemporal dynamics of neural ensembles and fields and the behavior they give rise to is extremely rich: they exhibit the full range of phase transitions along with interesting transient régimes that are neither fully ordered nor disordered in space and time.

Returning to where we started, this means that dynamic patterns and their pattern-generating dynamics are about the organization of matter, not (or not only) matter itself. With respect to the human brain, CD is about processes such as sniffing and smelling, listening and seeing, anticipating, moving and touching, feeling and deciding, choosing, learning, remembering and forgetting. It is about the restless mind at work in space and time, not only its contents. Thinking and thoughts go together.

Natural selection has created an enormous diversity of forms and patterns. It is not possible – nor does it make sense – to describe all of these at a molecular or atomic level, no more than to describe the huge and beautiful variety of crystalline forms. Nonequilibrium phase transitions and criticality are mechanisms that nature uses to create dynamic patterns of coordination in complex, heterogeneous systems, brains included. They provide ways to compress information and dimensionality in systems with uncountably large numbers of degrees of freedom and huge parameter spaces. The empirical and theoretical framework of CD offers a means to understand biological coordination in different creatures for diverse functions on multiple space and time scales. For CD, the reduction is to nature's strategic principles for functional pattern formation and change. It seems that only under quite peculiar circumstances – “making the familiar strange” as Sheets-Johnstone [35] would say – do basic laws for a qualitative and quantitative description of coordination emerge. One of these days, perhaps, the strange coordination dynamics of behavior and the brain, “simple” forms of which we have described here, may become familiar. Perhaps, the day will come when the interplay between criticality, multistability, and metastability, which allows neuronal assemblies qua coordinative structures to form, break, unite, dissolve, and harmonize in space and in time – “the dynamic brain in action” – will be realized. Without coordination, one suspects we would not be alive.

Acknowledgments

The research described herein is currently supported by grants from the National Institute of Mental Health (MH080838), the National Science Foundation (BCS0826897), the US Office of Naval Research (N000140910527), the Chaire d'Excellence Pierre de Fermat, and Florida Atlantic University. Much of the work described herein has depended on long-term support from these agencies and institutions, which are composed of people, friends, students, and colleagues, to whom the author is extremely grateful.

References

1. 1. Schrödinger, E. (1958) Mind and Matter, Cambridge University Press, Cambridge.
2. 2. Edelman, G.E. and Gally, J. (2001) Degeneracy and complexity in biological systems. Proc. Natl. Acad. Sci. U.S.A., 98, 13763–13768.
3. 3. Greenspan, R.J. (2012) Biological indeterminacy. Sci. Eng. Ethics, 18, 447–452. doi: 10.1007/s11948-012-9379-2
4. 4. Kelso, J.A.S. (2012) Multistability and metastability: understanding dynamic coordination in the brain. Philos. Trans. R. Soc., B, 367, 906–918.
5. 5. Kelso, J.A.S. and Tuller, B. (1984) in Handbook of Cognitive Neuroscience (ed. M.S. Gazzaniga), Plenum Press, New York, pp. 321–356.
6. 6. Beek, P.J., Peper, C.E., and Stegman, D.F. (1995) Dynamical models of movement coordination. Hum. Mov. Sci., 14, 573–608.
7. 7. Coey, C.A., Varlet, M., and Richardson, M.J. (2012) Coordination dynamics in a socially situated nervous system. Front. Hum. Neurosci., 6, 164. doi: 10.3389/fnhum.2012.00164
8. 8. Fuchs, A. and Jirsa, V.K. (eds) (2008) Coordination: Neural, Behavioral and Social Dynamics, Springer, Berlin.
9. 9. Huys, R. and Jirsa, V.K. (eds) (2010) Nonlinear Dynamics of Human Behavior, Springer-Verlag, Berlin, Heidelberg.
10. 10. Kelso, J.A.S. (1992) Coordination dynamics of human brain and behavior. Springer Proc. Phys., 69, 223234.
11. 11. Kelso, J.A.S. (1995) Dynamic Patterns: The Self Organization of Brain and Behavior, The MIT Press, Cambridge, MA, Paperback ed. 1997.
12. 12. Jirsa, V.K. and Kelso, J.A.S. (eds) (2004) Coordination Dynamics: Issues and Trends, Understanding Complex Systems, Springer Series in, Springer, Berlin, Heidelberg.
13. 13. Tschacher, W. and Dauwalder, J.P. (eds) (2003) The Dynamical Systems Approach to Cognition: Concepts and Empirical Paradigms Based on Self-Organization, Embodiment and Coordination Dynamics, World Scientific, Singapore.
14. 14. von der Malsburg, C., Phillips, W.A., and Singer, W. (eds) (2010) Dynamic Coordination in the Brain: From Neurons to Mind, Strüngmann Forum Report, vol. 5, MIT Press, Cambridge, MA.
15. 15. Fuchs, A. and Kelso, J.A.S. (2009) Movement coordination, in Encyclopedia of Complexity and System Science (ed. R.A. Meyers), Springer, Heidelberg.
16. 16. Oullier, O. and Kelso, J.A.S. (2009) Social coordination from the perspective of coordination dynamics, in Encyclopedia of Complexity and Systems Science (ed. R.A. Meyers), Springer, Heidelberg, pp. 8198–8212.
17. 17. Kelso, J.A.S. (2009) in Encyclopedia of Complexity and System Science (ed. R.A. Meyers), Springer, Heidelberg, pp. 1537–1564.
18. 18. Kelso, J.A.S. (2002) The complementary nature of coordination dynamics: self-organization and the origins of agency. J. Nonlinear Phenom. Complex Syst., 5, 364–371.
19. 19. Turvey, M.T. (2004) in Coordination Dynamics: Issues and Trends (eds V.K. Jirsa and J.A.S. Kelso), Springer, Berlin, Heidelberg, pp. 2–20.
20. 20. Scott, A. (1995) Stairway to the Mind, Springer-Verlag, New YorK.
21. 21. Kelso, J.A.S., Dumas, G., and Tognoli, E. (2013) Outline of a general theory of behavior and brain coordination. Neural Netw., 37, 120–131 (25th Commemorative Issue).
22. 22. Yates, F.E. (2008) Homeokinetics/homeodynamics: a physical heuristic for life and complexity. Ecol. Psychol., 20, 148–179.
23. 23. Kelso, J.A.S. (2008) An essay on understanding the mind. Ecol. Psychol., 20, 180–208.
24. 24. Wilson, K.G. (1979) Problems in physics with many scales of length. Scientific American, 241, 158–179.
25. 25. Kelso, J.A.S. and Haken, H. (1995) in What is Life? The Next 50 Years (eds M. Murphy and L. O'Neill), Cambridge University Press, pp. 137–160.
26. 26. Raichle, M.E. (2010) Two views of brain function. Trends Cognit. Sci., 14, 180–190.
27. 27. Deco, G., Jirsa, V.K., and Mc Intosh, A.R. (2011) Emerging concepts for the dynamical organization of resting state activity in the brain. Nat. Rev. Neurosci., 12, 43–56.
28. 28. van Hemmen, J.L. and Sejnowski, T.J. (eds) (2006) 23 Problems in Systems Neuroscience, Oxford University, Oxford.
29. 29. Martin, K.A.C. (2006) Where are the switches on this thing? Asking the big questions in neuroscience. Nature, 440, 1113–1114.
30. 30. Weyl, H. (1952) Symmetry, Princeton University Press, Princeton, NJ.
31. 31. Dai, L., Vorselen, D., Korolev, K.S., and Gore, J. (2012) Generic indicators for loss of resilience before a tipping point leading to population collapse. Science, 336, 1175–1177.
32. 32. Scheffer, M., Carpenter, S.R., Lenton, T., Bascompte, J. et al. (2012) Anticipating critical transitions. Science, 338, 344–348.
33. 33. Kelso, J.A.S. (2010) Instabilities and phase transitions in human brain and behavior. Front. Hum. Neurosci., 4, 23. doi: 10.3389/fnhum.2010.00023
34. 34. Wade, J.J., McDaid, L.J., Harkin, J., Crunelli, V., and Kelso, J.A.S. (eds) (2013) Biophysically-based computational models of astrocyte∼neuron coupling and their functional significance. Front. Comput. Neurosci. (e-book).
35. 35. Sheets-Johnstone, M. (2011) The Primacy of Movement, Expanded 2nd edn, John Benjamins, Amsterdam.
36. 36. Gleick, J. (2003) Isaac Newton, Pantheon, New York.
37. 37. Crease, R.P. (2012) Critical Point: Primate Physics. Physics World (Nov.), p. 18.
38. 38. Pattee, H.H. (1979) in A Question of Physics (eds P. Buckley and F.D. Peat), University of Toronto Press, Toronto & Buffalo, p. 85.
39. 39. May, R.M. (1976) Simple mathematical models with very complicated dynamics. Nature, 261, 459–467.
40. 40. Katchalsky, A.K., Rowland, V., and Blumenthal, R. (1974) Dynamic patterns of brain cell assemblies. Neurosci. Res. Program Bull., 12 (1), 1–187.
41. 41. Rabinovich, M.I., Friston, K.J., and Varona, P. (2012) Principles of Brain Dynamics, The MIT Press, Cambridge, MA.
42. 42. Kelso, J.A.S., Southard, D., and Goodman, D. (1979) On the nature of human interlimb coordination. Science, 203, 1029–1031.
43. 43. Kelso, J.A.S., Tuller, B., Bateson, E.V., and Fowler, C.A. (1984) Functionally specific articulatory cooperation following jaw perturbations during speech: evidence for coordinative structures. J. Exp. Psych: Hum. Percept. Perform., 10, 812–832.
44. 44. Turvey, M.T. (2007) Action and perception at the level of synergies. Hum. Mov. Sci., 26, 657–697.
45. 45. Turvey, M.T. and Carello, C. (2012) On intelligence from first principles: guidelines for inquiry into the hypothesis of physical intelligence (PI). Ecol. Psychol., 24, 3–32.
46. 46. Maynard-Smith, J. and Szathmary, E. (1995) The Major Transitions in Evolution, Freeman Press, Oxford.
47. 47. Corning, P.A. (2005) Holistic Darwinism, University of Chicago Press, Chicago and London.
48. 48. Wilson, D.S., Hayes, S.C., Biglan, A., and Embry, D.D. (2014) Evolving the future: toward a science of intentional change. Behav. Brain Sci. (in press).
49. 49. Kostrubiec, V. and Kelso, J.A.S. (2014) Incorporating coordination dynamics into an evolutionarily-grounded science of intentional change. Behav. Brain Sci. (in press).
50. 50. Haken, H. (1977/83) Synergetics, an Introduction: Non-Equilibrium Phase Transitions and Self-Organization in Physics, Chemistry and Biology, Springer, Berlin.
51. 51. DeLuca, C., Jantzen, K.J., Comani, S., Bertollo, M., and Kelso, J.A.S. (2010) Striatal activity during intentional switching depends on pattern stability. J. Neurosci., 30 (9), 3167–3174.
52. 52. Briggman, K.L. and Kristan, W.B. (2008) Multifunctional pattern-generating circuits. Ann. Rev. Neurosci., 31, 271–294.
53. 53. Grillner, S. (1975) Locomotion in vertebrates: central mechanisms and reflex interaction. Physiol. Rev., 55 (2), 247–304.
54. 54. Grillner, S. (1985) Neurobiological bases of rhythmic motor acts in vertebrates. Science, 228, 143–149.
55. 55. Grillner, S. (2011) Human locomotor circuits conform. Science, 334, 912–913.
56. 56. Marder, E. (2001) Moving rhythms. Nature, 410, 755.
57. 57. Marder, E. and Bucher, D. (2001) Central pattern generators and the control of rhythmic movements. Curr. Biol., 11, R986–R996.
58. 58. Marder, E. and Bucher, D. (2007) Understanding circuit dynamics using the stomatogastric ganglion of lobsters and crabs. Ann. Rev. Physiol., 69, 291–316.
59. 59. Selverston, A.I. (1980) Are central pattern generators understandable? Behav. Brain Sci., 3, 535–571. doi: 10.1017/S0140525X00006580
60. 60. Selverston, A.I. (1987) Invertebrate central pattern generators as computational data bases, in Dynamic Patterns in Complex Systems (eds J.A.S. Kelso, A.J. Mandell, and M.F. Shlesinger), World Scientific, Singapore.
61. 61. Buzsáki, G. (2006) Rhythms of the Brain, Oxford University Press, Oxford.
62. 62. Buzsáki, G. and Draguhn, A. (2004) Neuronal oscillations in cortical networks. Science, 304, 1926–1929.
63. 63. Buzsáki, G. and Watson, B.O. (2012) Brain rhythms and neural syntax: implications for efficient coding of cognitive content and neuropsychiatric disease. Dialogues Clin. Neurosci., 14, 345–367.
64. 64. Yuste, R., MacLean, J.N., Smith, J., and Lansner, A. (2005) The cortex as a central pattern generator. Nat. Rev. Neurosci., 6, 477–483.
65. 65. Winfree, A.T. (1987) The Timing of Biological Clocks, W.H. Freeman, New York.
66. 66. Delcomyn, F. (1980) Neural basis of rhythmic behavior in animals. Science, 210, 492–498.
67. 67. Tuller, B., Harris, K.S., and Kelso, J.A.S. (1982) Stress and rate: differential transformations of articulation. J. Acoust. Soc. Am., 71, 1534–1543.
68. 68. Feldman, A.G. (1966) Functional tuning of the nervous system with control of movement or maintenance of a steady posture. II. Controllable parameters of the muscle. Biophysics, 11, 565–578.
69. 69. Kelso, J.A.S. (1977) Motor control mechanisms underlying human movement reproduction. J. Exp. Psychol. Hum. Percept. Perform., 3, 529543.
70. 70. Polit, A. and Bizzi, E. (1978) Processes controlling arm movements in monkeys. Science, 201, 1235–1237.
71. 71. Kelso, J.A.S., Holt, K.G., Kugler, P.N., and Turvey, M.T. (1980) in Tutorials in Motor Behavior (eds G.E. Stelmach and J. Requin), North Holland, Amsterdam, pp. 49–70.
72. 72. Baar, E. (2004) Memory and Brain Dynamics: Oscillations Integrating Attention, Perception, Learning, and Memory, CRC Press, Boca Raton, FL.
73. 73. Singer, W. (2005) The brain—an orchestra without a conductor. Max Planck Res., 3, 15–18.
74. 74. Kelso, J.A.S., Holt, K.G., Rubin, P., and Kugler, P.N. (1981) Patterns of human interlimb coordination emerge from the properties of nonlinear oscillatory processes: theory and data. J. Motor Behav., 13, 226–261.
75. 75. Kugler, P.N., Kelso, J.A.S., and Turvey, M.T. (1980) in Tutorials in Motor Behavior (eds G.E. Stelmach and J. Requin), North Holland, Amsterdam, pp. 1–40.
76. 76. Feldman, A.G. (2009) in Progress in Motor Control V. A Multidisciplinary Perspective (ed. D. Sternad), Springer, New York, pp. 637–644.
77. 77. Feldman, A.G. and Levin, M.F. (1995) The origin and use of positional frames of reference in motor control. Behav. Brain Sci., 18, 723–744.
78. 78. Latash, M.L. (2012) Fundamentals of Motor Control, Academic Press, New York.
79. 79. Kelso, J.A.S. (1981) On the oscillatory basis of movement. Bull. Psychonomic Soc., 18, 63.
80. 80. Kelso, J.A.S. (1984) Phase transitions and critical behavior in human bimanual coordination. Am. J. Physiol.: Regul. Integr. Comp., 15, R1000–R1004.
81. 81. Kostrubiec, V., Zanone, P.-G., Fuchs, A., and Kelso, J.A.S. (2012) Beyond the blank slate: routes to learning new coordination patterns depend on the intrinsic dynamics of the learner – experimental evidence and theoretical model. Front. Hum. Neurosci., 6, 212. doi: 10.3389/fnhum.2012.00222
82. 82. Zanone, P.G. and Kelso, J.A.S. (1992) The evolution of behavioral attractors with learning: Nonequilibrium phase transitions. J. Exp. Psychol.: Hum. Percept. Perform., 18 (2), 403421.
83. 83. Howard, I.S., Ingram, J.N., Körding, K.P., and Wolpert, D.M. (2009) Statistics of natural movements are reflected in motor errors. J. Neurophysiol., 102, 1902–1910.
84. 84. Prinz, A.A., Bucher, D., and Marder, E. (2004) Similar network activity from disparate circuit parameters. Nat. Neurosci., 7, 1345–1352.
85. 85. Haken, H., Kelso, J.A.S., and Bunz, H. (1985) A theoretical model of phase transitions in human hand movements. Biol. Cybern., 51, 347–356.
86. 86. Liese, T. and Cohen, A. (2005) Nonlinear oscillators at our fingertips. Am. Math. Mon., 114, 14–28.
87. 87. Jirsa, V.K., Friedrich, R., Haken, H., and Kelso, J.A.S. (1994) A theoretical model of phase transitions in the human brain. Biol. Cybern., 71, 2735.
88. 88. Banerjee, A., Tognoli, E., Kelso, J.A.S and Jirsa, V.K. (2012) Spatiotemporal reorganization of large-scale neural assemblies mediates bimanual coordination. Neuroimage, 62, 1582–1592. doi: org/10.1016/j.neuroimage.2012.05.046
89. 89. Calvin, S. and Jirsa, V.K. (2010) Perspectives on the dynamic nature of coupling in human coordination, in Nonlinear Dynamics of Human Behavior (eds R. Huys and V.K. Jirsa), Springer-Verlag, Berlin, Heidelberg.
90. 90. Kubo, R. (1966) The fluctuation-dissipation theorem. Rep. Prog. Phys., 29, 255–283.
91. 91. Scholz, J.P., Kelso, J.A.S., and Schöner, G. (1987) Nonequilibrium phase transitions in coordinated biological motion: critical slowing down and switching time. Phys. Lett. A, 8, 390–394.
92. 92. Kelso, J.A.S., Schöner, G., Scholz, J.P., and Haken, H. (1987) Phaselocked modes, phase transitions and component oscillators in coordinated biological motion. Phys. Scripta, 35, 79–87.
93. 93. Kelso, J.A.S., Scholz, J.P., and Schöner, G. (1986) Nonequilibrium phase transitions in coordinated biological motion: critical fluctuations. Phys. Lett. A, 118, 279–284.
94. 94. Schöner, G. and Kelso, J.A.S. (1988) Dynamic pattern generation in behavioral and neural systems. Science, 239, 1513–1520.
95. 95. Buchanan, J.J. and Kelso, J.A.S. (1993) Posturally induced transitions in rhythmic multijoint limb movements. Exp. Brain Res., 94, 131–143.
96. 96. Schöner, G., Haken, H., and Kelso, J.A.S. (1986) A stochastic theory of phase transitions in human hand movement. Biol. Cybern., 53, 247–257.
97. 97. Haken, H. (1988) Information and Self-Organization, Springer, Berlin.
98. 98. Daffertshofer, A. (2010) Benefits and pitfalls in analyzing noise in dynamical systems – On stochastic differential equations and system identification, in Nonlinear Dynamics of Human Behavior (eds R. Huys and V.K. Jirsa), Springer-Verlag, Berlin, Heidelberg.
99. 99. Chialvo, D. (2010) Emergent complex neural dynamics. Nat. Phys., 6, 744–750.
100. 100. Chen, Y., Ding, M., and Kelso, J.A.S. (1997) Long term memory processes (1/f^α type) in human coordination. Phys. Rev. Lett., 79, 4501–4504.
101. 101. Chen, Y., Ding, M., and Kelso, J.A.S. (2003) in Processes with Long-Range Correlations (eds G. Rangarajan and M. Ding), Springer, Berlin, pp. 309–323.
102. 102. Ding, M., Chen, Y., and Kelso, J.A.S. (2002) Statistical analysis of timing errors. Brain Cognit., 48, 98–106.
103. 103. Treffner, P.J. and Kelso, J.A.S. (1999) Dynamic encounters: long memory during functional stabilization. Ecol. Psychol., 11, 103–137.
104. 104. Beggs, J.M. and Timme, N. (2012) Being critical of criticality in the brain. Front. Physiol., 3, 163.
105. 105. Kelso, J.A.S. and Tuller, B. (1981) Toward a theory of apractic syndromes. Brain Lang., 12, 224–245.
106. 106. Jirsa, V.K. and Kelso, J.A.S. (2000) Spatiotemporal pattern formation in neural systems with heterogeneous connection topologies. Phys. Rev. E, 62, 8462–8465.
107. 107. Bressler, S.L. and Kelso, J.A.S. (2001) Cortical coordination dynamics and cognition. Trends Cognit. Sci., 5, 26–36.
108. 108. Kelso, J.A.S., DelColle, J., and Schöner, G. (1990) Action-perception as a pattern formation process, in Attention and Performance XIII (ed. M. Jeannerod), Erlbaum, Hillsdale, NJ, pp. 139–169.
109. 109. Kelso, J.A.S. (1991) Behavioral and neural pattern generation: the concept of Neurobehavioral Dynamical System (NBDS), in Cardiorespiratory and Motor Coordination (eds H.P. Koepchen and T. Huopaniemi), Springer-Verlag, Berlin.
110. 110. Kelso, J.A.S. and Tognoli, E. (2007) Toward a complementary neuroscience: metastable coordination dynamics of the brain, in Neurodynamics of Higher-level Cognition and Consciousness (eds R. Kozma and L. Perlovsky), Springer, Heidelberg.
111. 111. Edelman, G.M. (2004) Naturalizing consciousness: a theoretical framework. Proc. Natl. Acad. Sci. U.S.A., 100, 520–524.
112. 112. Edelman, G. and Tononi, G. (2000) A Universe of Consciousness, Basic Books, New York.
113. 113. Fingelkurts, A.A. and Fingelkurts, A.A. (2004) Making complexity simpler: multivariability and metastability in the brain. Int. J. Neurosci., 114, 843–862.
114. 114. Freeman, W.J. and Holmes, M.D. (2005) Metastability, instability, and state transition in neocortex. Neural Netw., 18, 497–504.
115. 115. Friston, K.J. (1997) Transients, metastability, and neuronal dynamics. Neuroimage, 5, 164–171.
116. 116. Koch, C. (2005) The Quest for Consciousness, Roberts and Co., Englewood, CO.
117. 117. Sporns, O. (2004) in Coordination Dynamics: Issues and Trends (eds V.K. Jirsa and J.A.S. Kelso), Springer-Verlag, Berlin, pp. 197–215.
118. 118. Sporns, O. (2010) Networks of the Brain, MIT Press, Cambridge.
119. 119. Varela, F.J., Lachaux, J.-P., Rodriguez, E., and Martinerie, J. (2001) The brainweb: phase synchronization and large-scale integration. Nat. Rev. Neurosci., 2, 229–239.
120. 120. Rabinovich, M.I., Huerta, R., and Laurent, G. (2008) Transient dynamics for neural processing. Science, 321, 48–50.
121. 121. Chen, Y., Ding, M., and Kelso, J.A.S. (2003) Task-related power and coherence changes in neuromagnetic activity during visuomotor coordination. Exp. Brain Res., 148, 105–116.
122. 122. Dumas, G., Chavez, M., Nadel, J. and Martinerie, J. (2012) Anatomical connectivity influences both intra- and inter-brain synchronizations. PLoS ONE 7 (5), e36414. doi: 10.1371/journal.pone.0036414.
123. 123. Tognoli, E., Lagarde, J., DeGuzman, G.C., and Kelso, J.A.S. (2007) The phi complex as a neuromarker of human social coordination. Proc. Natl. Acad. Sci., 104, 8190–8195 (from the cover; see also Scientific American Mind, August, 2007).
124. 124. Begleiter, H. and Porjesz, B. (2006) Genetics of human brain oscillations. Int. J. Psychophysiol., 60, 162–171.
125. 125. Whittington, M.A., Traub, R.D., Kopell, N., Ermentrout, B., and Buhl, E.H. (2000) Inhibition-based rhythms: experimental and mathematical observations on network dynamics. Int. J. Psychophysiol., 38, 315–336.
126. 126. Wade, J.J., McDaid, L.J., Harkin, J.G., Crunelli, V., and Kelso, J.A.S. (2011) Bidirectional coupling between astrocytes and neurons mediates learning and dynamic coordination in the brain: a multiple modeling approach. PLoS One, 6, e29445.
127. 127. Womelsdorf, T., Schoffelen, J.-M., Oostenveld, R., Singer, W., Desimone, R., Engel, A.K., and Fries, P. (2007) Modulation of neuronal interactions through neuronal synchronization. Science, 316, 1609–1612.
128. 128. Canolty, R.T., Edwards, E., Dalal, S.S., Soltani, M., Nagarajan, S.S., Kirsch, H.E., Berger, M.S., Barbaro, N.M., and Knight, R.T. (2006) High gamma power is phase-locked to theta oscillations in human neocortex. Science, 313, 1626–1628.
129. 129. Fries, P. (2009) Neuronal gamma-band synchronization as a fundamental process in cortical computation. Ann. Rev. Neurosci., 32, 209–224.
130. 130. Haken, H. (1996) Principles of Brain Functioning, Springer, Berlin.
131. 131. Van Orden, G.C., Holden, J.G., and Turvey, M.T. (2005) Human cognition and 1/f scaling. J. Exp. Psychol. Gen., 134, 117–123.
132. 132. Oullier, O., DeGuzman, G.C., Jantzen, K.J., Lagarde, J., and Kelso, J.A.S. (2008) Social coordination dynamics: measuring human bonding. Social Neurosci., 3, 178–192. doi: 10.1080/17470910701563392
133. 133. Schmidt, R.C. and Richardson, M.J. (2008) Dynamics of interpersonal coordination, in Coordination: Neural, Behavioral and Social Dynamics (eds A. Fuchs and V.K. Jirsa), Springer, Berlin.
134. 134. Plenz, D. and Thiagarian, T. (2007) The organizing principles of neuronal avalanche activity: cell assemblies and cortex. Trends Neurosci., 30, 101–110.
135. 135. Plenz, D. (2013) The critical brain. Physics, 6, 47.
136. 136. Kelso, J.A.S. (2001) Metastable coordination dynamics of brain and behavior. Brain Neural Networks (Jpn.), 8, 125–130.
137. 137. Kelso, J.A.S. (2001) How the brain changes its mind. in: The Emergence of the Mind, Fondazione Carlo Erba, Milano, pp. 93–101.
138. 138. Rabinovich, M.I. and Varona, P. (2012) Transient brain dynamics, in Principles of Brain Dynamics (eds M.I. Rabinovich, K.J. Friston, and P. Varona), The MIT Press, Cambridge, MA.
139. 139. Fuchs, A., Kelso, J.A.S., and Haken, H. (1992) Phase transitions in the human brain: Spatial mode dynamics. Int. J. Bifurcation Chaos, 2, 917939.
140. 140. Fuchs, A., Deecke, L., and Kelso, J.A.S. (2000) Phase transitions in human brain revealed by large SQuID arrays: response to Daffertshofer, Peper and Beek. Phys. Lett. A, 266, 303–308.
141. 141. Fuchs, A., Jirsa, V.K., and Kelso, J.A.S. (2000) Theory of the relation between human brain activity (MEG) and hand movements. Neuroimage, 11, 359–369.
142. 142. Fuchs, A., Mayville, J.M., Cheyne, D., Weinberg, H., Deecke, L., and Kelso, J.A.S. (2000) Spatiotemporal analysis of neuromagnetic events underlying the emergence of coordinative instabilities. Neuroimage, 12, 71–84.
143. 143. Kelso, J.A.S., Bressler, S.L., Buchanan, S., DeGuzman, G.C., Ding, M., Fuchs, A., and Holroyd, T. (1991) Cooperative and critical phenomena in the human brain revealed by multiple SQUIDS, in Measuring Chaos in the Human Brain (eds D. Duke and W. Pritchard), World Scientific, New Jersey, pp. 97–112.
144. 144. Kelso, J.A.S., Bressler, S.L., Buchanan, S., DeGuzman, G.C., Ding, M., Fuchs, A., and Holroyd, T. (1992) A phase transition in human brain and behavior. Phys. Lett. A, 169, 134–144.
145. 145. Kelso, J.A.S. and Fuchs, A. (1995) Selforganizing dynamics of the human brain: critical instabilities and Sil'nikov chaos. Chaos, 5 (1), 64–69.
146. 146. Mayville, J.M., Fuchs, A., Ding, M., Cheyne, D., Deecke, L., and Kelso, J.A.S. (2001) Event-related changes in neuromagnetic activity associated with syncopation and synchronization tasks. Hum. Brain Mapp., 14, 65–80.
147. 147. Banerjee, A., Tognoli, E., Jirsa, V.K., Assisi, C., and Kelso, J.A.S. (2008) Mode Level Cognitive Subtraction (MLCS) quantifies spatiotemporal reorganization in large-scale brain topographies. Neuroimage, 15, 663–674.
148. 148. Mayville, J.M., Bressler, S.L., Fuchs, A., and Kelso, J.A.S. (1999) Spatiotemporal reorganization of electrical activity in the human brain associated with a phase transition in rhythmic auditory-motor coordination. Exp. Brain Res., 127, 371–381.
149. 149. Wallenstein, G.V., Kelso, J.A.S., and Bressler, S.L. (1995) Phase transitions in spatiotemporal patterns of brain activity and behavior. Physica D, 84, 626–634.
150. 150. Mayville, J.M., Jantzen, K.J., Fuchs, A., Steinberg, F.L., and Kelso, J.A.S. (2002) Cortical and subcortical networks underlying syncopated and synchronized coordination tasks revealed using functional MRI. Hum. Brain Mapp., 17, 214–229.
151. 151. Oullier, O., Jantzen, K.J., Steinberg, F.L., and Kelso, J.A.S. (2005) Neural substrates of real and imagined sensorimotor coordination. Cereb. Cortex, 15 (7), 975–985.
152. 152. Meyer-Lindenberg, A., Zieman, U., Hajak, G., Cohen, L., and Berman, K. (2002) Transition between dynamical states of differing stability in the human brain. Proc. Natl. Acad. Sci. U.S.A., 99, 10948–10953.
153. 153. Jantzen, K.J., Steinberg, F.L., and Kelso, J.A.S. (2009) Coordination dynamics of large-scale neural circuitry underlying sensorimotor behavior. J. Cognit. Neurosci., 21, 2420–2433. doi: 10.1162/jocn.2008.21182
154. 154. Oullier, O., Lagarde, J., Jantzen, K.J., and Kelso, J.A.S. (2006) Dynamiques comportementale et cérébrale des coordinations sensorimotrices: (in)stabilité et metastabilité rythmiques. J. Soc. Biol., 200 (2), 145–167. (Medline Version: Coordination Dynamics: (in)stability and metastability in behavioural and neural systems. J. Soc. Biol., 200(2), 145-167).
155. 155. Jantzen, K.J., Steinberg, F.L., and Kelso, J.A.S. (2004) Brain networks underlying timing behavior are influenced by prior context. Proc. Natl. Acad. Sci. U.S.A., 101, 6815–6820.
156. 156. Jantzen, K.J., Anderson, B., Steinberg, F.L., and Kelso, J.A.S. (2004) A prospective functional magnetic resonance imaging study of Mild Traumatic Brain Injury (MTBI) in college football players. Am. J. Neuroradiol., 25, 738–745.
157. 157. Houweling, S., Beek, P.J., and Daffertshofer, A. (2010) Spectral changes of interhemispheric cross talk during movement instabilities. Cereb. Cortex, 20, 2605–2613.
158. 158. Uhl, C., Friedrich, R., and Haken, H. (1995) Analysis of spatiotemporal signals of complex systems. Phys. Rev. E: Stat. Phys. Plasmas Fluids Relat. Interdisciplin. Top., 51 (5), 3890–3900.
159. 159. Jirsa, V.K. and Haken, H. (1996) Field theory of electromagnetic brain activity. Phys. Rev. Lett., 77, 960–963.
160. 160. Jirsa, V. and Haken, H. (1997) A derivation of a macroscopic field theory of the brain from the quasi-microscopic neural dynamics. Physica D (Nonlinear Phenom.), 99, 503–526.
161. 161. Frank, T.D., Daffertshofer, A., Peper, C.E., Beek, P.J., and Haken, H. (2000) Towards a comprehensive theory of brain activity: coupled oscillator systems under external forces. Physica D, 144, 62–86.
162. 162. Kelso, J.A.S., Fuchs, A., Holroyd, T., Lancaster, R., Cheyne, D., and Weinberg, H. (1998) Dynamic cortical activity in the human brain reveals motor equivalence. Nature, 392, 814–818.
163. 163. Jirsa, V.K., Fuchs, A., and Kelso, J.A.S. (1998) Connecting cortical and behavioral dynamics: bimanual coordination. Neural Comput., 10, 2019–2045.
164. 164. Beek, P.J., Peper, C.E., and Daffertshofer, A. (2002) Modeling rhythmic interlimb coordination: beyond the Haken–Kelso–Bunz Model. Brain Cognition, 48 (1), 149–165. doi: 10.1006/brcg.2001.1310
165. 165. Carson, R.G. (2005) Neural pathways mediating bilateral interactions between the upper limbs. Brain Res., 49, 641–622.
166. 166. Daffertshofer, A., Peper, C.E., Frank, T.D. and Beek, P.J. (2000) Spatio-temporal patterns of encephalographic signals during polyrythmic tapping. Human Movement Sci., 19, 475–498.
167. 167. Daffertshofer, A., Peper, C.E., and Beek, P.J. (2005) Stabilization of bimanual coordination due to active inhibition: a dynamical account. Biol. Cybern., 92, 101–109.
168. 168. Swinnen, S.P. (2002) Intermanual crosstalk: from behavioural models to neural-network interactions. Nat. Neurosci., 3, 350–361.
169. 169. Assisi, C.G., Jirsa, V.K., and Kelso, J.A.S. (2005) Synchrony and clustering in heterogeneous networks with global coupling and parameter dispersion. Phys. Rev. Lett., 94, 018106.
170. 170. Deco, G., Jirsa, V.K., and Friston, K.J. (2012) The dynamical and structural basis of brain activity, in Principles of Brain Dynamics (eds M.I. Rabinovich, K.J. Friston, and P. Varona), The MIT Press, Cambridge, MA.
171. 171. Kelso, J.A.S., Fuchs, A., and Jirsa, V.K. (1999) Traversing scales of brain and behavioral organization, in Analysis of Neurophysiological Brain Functioning (ed. C. Uhl), Springer-Verlag, Berlin, pp. 73–125.
172. 172. Kelso, J.A.S., Jirsa, V.K., and Fuchs, A. (1999) From level to level in brain and behavior, in Statistical Physics on the Eve of the 21st Century (eds M.T. Bachelor and L.T. Wille), World Scientific, Singapore, pp. 113–130.
173. 173. Daffertshofer, A. and van Wijk, C.M. (2012) Transient motor behavior and synchronization in the cortex, in Principles of Brain Dynamics (eds M.I. Rabinovich, K.J. Friston, and P. Varona), The MIT Press, Cambridge, MA.
174. 174. Freeman, W.J. (1975) Mass Action in the Nervous System, Academic Press, New York.
175. 175. Jantzen, K.J., Fuchs, A., Mayville, J.M., and Kelso, J.A.S. (2001) Neuromagnetic activity in alpha and beta bands reflects learning-induced increases in coordinative stability. Clin. Neurophysiol., 112, 1685–1697.
176. 176. Temprado, J.J., Zanone, P.G., Monno, A., and Laurent, M. (1999) Attentional load associated with performing and stabilizing preferred bimanual patterns. J. Exp. Psych: Hum. Percept. Perform., 25, 1595–1608.
177. 177. Riley, M.A., Richardson, M.C., Shockley, K., and Ramenzoni, V.C. (2011) Interpersonal synergies. Front. Psychol., 2, 38. doi: 10.3389/fpsyg.2011.00038
178. 178. Kelso, J.A.S., DeGuzman, G.C., Reveley, C., and Tognoli, E. (2009) Virtual Partner Interaction (VPI): exploring novel behaviors via coordination dynamics. PLoS One, 4 (6), e5749.
179. 179. Prinz, A.A., Abbott, L.F., and Marder, E. (2004) The dynamic clamp comes of age. Trends Neurosci., 27, 218–224.
180. 180. Lagarde, J. and Kelso, J.A.S. (2006) Binding of movement, sound and touch: multimodal coordination dynamics. Exp. Brain Res., 173, 673–688.
181. 181. Bohr, N. (1948) On the notions of causality and complementarity. Dialectica, 2, 312. Cited In Pais, A., Niels Bohr's Times, Oxford University Press, Oxford, p. 433.
182. 182. Abrams, D.M. and Strogatz, S.H. (2006) Chimera states in a ring of nonlocally coupled oscillators. Int. J. Bifurc. Chaos, 16, 21–37.
183. 183. Kuramoto, Y. and Battogtokh, D. (2002) Coexistence of coherence and incoherence in nonlocally coupled phase oscillators: a soluble case. J. Nonlin. Phenom. Complex Syst., 5 (4), 380–385.
184. 184. Shanahan, M. (2010) Metastable chimera states in community structured oscillator networks. Chaos, 20 (1), 013108.
185. 185. Kelso, J.A.S. and Tognoli, E. (2010) Spatiotemporal metastability: design for a brain. Soc. Neurosci., San Diego, 343, 16.
186. 186. Tognoli, E. and Kelso, J.A.S. (2014) The metastable brain. Neuron, 81, 35–48.
187. 187. Dumas, G., Nadel, J., Soussignan, R., Martinerie, J., and Garnero, L. (2010) Inter-brain synchronization during social interaction. PLoS One, 5 (8), e12166. doi: 10.1371/journal.pone.0012166
188. 188. Kelso, J.A.S. (2009) Synergies: atoms of brain and behavior. Adv. Exp. Med. Biol., 629, 83–91.(Also Sternad, D. (ed.) A Multidisciplinary Approach to Motor Control, Springer, Heidelberg).
189. 189. Tognoli, E. (2008) EEG coordination dynamics: neuromarkers of social coordination, in Coordination: Neural, Behavioral and Social Dynamics (eds A. Fuchs and V.K. Jirsa), Springer, Berlin.
190. 190. Huys, R., Studenka, B.E., Rheame, N., Zelaznik, H.N., and Jirsa, V.K. (2008) Distinct timing mechanisms produce discrete and continuous movements. PLoS Comput. Biol., 4, e1000061.
191. 191. Huys, R., Perdikis, D., and Jirsa, V.K. (2014) Functional architectures and structured flows on manifolds: a dynamical framework for perceptual-motor behavior. Psych. Rev. (in press).
192. 192. Jirsa, V.K. and Kelso, J.A.S. (2005) The excitator as a minimal model for the coordination dynamics of discrete and rhythmic movements. J. Motor Behav., 37, 35–51.
193. 193. Laughlin, R.B. and Pines, D. (2000) The theory of everything. Proc. Natl. Acad. Sci. U.S.A., 97, 28–31.
194. 194. Anderson, P.W. (1972) More is different. Science, 177, 393–396.
195. 195. Perdikis, D., Huys, R., and Jirsa, V.K. (2011) Time scale hierarchies in the functional organization of complex behaviors. PLoS Comput. Biol., 7 (9), e1002198. doi: 10.1371/journal.pcbi.1002198
196. 196. Kelso, J.A.S. (2005) The complementary nature of coordination dynamics: toward a science of the in-between, in Uncertainty and Surprise, vol. 3 (eds R. Mc Daniel and D. Driebe), Springer Series in Understanding Complex Systems, Springer-Verlag, Berlin, Heidelberg.
197. 197. Kelso, J.A.S. and Engström, D.A. (2006) The Complementary Nature, MIT Press, Cambridge, MA. (Paperback Edition March 2008).
198. 198. Newell, K.M., Liu, Y.-T., and Mayer-Kress, G.M. (2008) Landscapes beyond the HKB model, in Coordination: Neural, Behavioral and Social Dynamics (eds A. Fuchs and V.K. Jirsa), Springer, Berlin, Heidelberg.
199. 199. Park, H. and Turvey, M.T. (2008) Imperfect symmetry and the elementary coordination law, in Coordination: Neural, Behavioral and Social Dynamics (eds A. Fuchs and V.K. Jirsa), Springer, Berlin, Heidelberg.

¹ The word “process” is chosen carefully. What we call a structure in biology (say a bone, or a piece of a creature's neuroanatomy) or an institution in sociology is a slowly evolving process. Such processes range across many scales of magnitude and functioning timescales.

² One might argue that the recent notion of so-called resting state networks – spontaneous coherent brain activity in the absence of any task (see [26] for review) – qualifies as an example of self-organizing coordinative structures. Theoretical research has indeed hypothesized that the brain's resting state dynamics operates close to criticality (see, e.g., [27] for a review, and papers by Plenz, Chialvo, Breakspear, and others in this book). Empirical evidence suggests that resting-state networks number between 6 and 10 and appear to be related to vision, audition, attention, and so forth. Similar to resting-state networks, coordinative structures are low-dimensional representations of typically very high-dimensional systems, but they are not a tidy set of fixed patterns nor are they restricted in number.

³ Just as neuroscience, until quite recently, has not in general looked to contemporary physical theories of cooperative phenomena to help provide “a picture of the dynamic brain” never mind the principles for how the brain works (but see [40] and for a modern example, [41]).

⁴ Coordinative structures are synonymous with the term synergy – which has a long and checkered history in many fields of inquiry. Coordinative structures are preferred here because they are an expression of both structure (the context-dependent elements and their interaction) and function (e.g., when an organism moves purposely to accomplish a goal). One imagines that coordinative structures are used to accomplish many behavioral, cognitive, and affective functions.

⁵ The equilibrium point hypothesis continues to be actively explored in the field of motor control (e.g., [76–78]) but will not concern us further here.

⁶ It might seem to some that just as an apple falling on one's head or a ball rolling down an inclined plane are very limited examples of inanimate motion, bimanual finger movements constitute a very limited example of human behavior. That's hardly the point. Nevertheless, recent work in Daniel Wolpert's group [83], shows that the same effects occur in a wide variety of natural everyday tasks recorded over 30 h, namely, symmetric and antisymmetric movements are predominant at low frequencies, whereas only symmetric movements are predominant at high frequencies.

⁷ A detailed mathematical analysis by Liese and Cohen [86], which earned them the Ford Prize of the American Mathematical Society, derives the potential function starting from a theoretical model system of nonlinearly coupled nonlinear oscillators (as opposed to the other way round in HKB where the simplest nonlinear coupling was chosen – eventually found to be biophysically relevant [87] – and the functional form of the nonlinear oscillators was based on empirical knowledge).

⁸ At an early presentation of this work [92], the late Rolf Landauer (1927–1999) suggested that we call it a limiting case of a first-order transition. This is a technical point.

⁹ Coexistent states are well known in fluid dynamics, where the classical example is the onset of turbulence in fluid flow through a pipe. Linear stability analysis is unusual because it predicts that the laminar flow is always stable for any Reynolds number Re. However, as a function of Re, the lowest eigenvalue approaches zero asymptotically. In reality, imperfections in the pipe and in the energy injection cause bursts of turbulence (plugs) to be observed also at finite Re, such that the flows shows laminar section with intermittent plugs of turbulence (I. Procaccia, personal communication, 24 August 2012).