11
Single Neuron Response Fluctuations: A Self-Organized Criticality Point of View

Asaf Gal and Shimon Marom

Criticality and self-organized criticality (SOC) are concepts often used to explain and think about the dynamics of large-scale neural networks. This is befitting, if one adopts, as common, the description of neural networks as large ensembles of interacting elements. The criticality framework provides an attractive (but not unique) explanation of the abundance of scale-free statistics and fluctuations in the activity of neural networks both in vitro and in vivo, as measured by various means [1–3]. While similar phenomena, including scale-free fluctuations and power-law-distributed event sizes, are observed also at the level of single neurons [4–8], the application of criticality concepts to single neuron dynamics seems less natural. Indeed, in modern theoretical neuroscience, single neurons are mostly taken as the fundamental, simple “atomic” elements of neural systems. These elements are usually attributed with stereotypical dynamics, with the fine details being stripped away in favor of “computational simplicity,” thus off-loading the emergent complexity to the population level. On the other hand, “detailed” modeling approaches fit neuronal dynamics using extremely elaborated, high-dimensional, multiparameter, spatiotemporal mathematical models. In this chapter, we demonstrate that using concepts borrowed from the physics of critical phenomena offers a different, intermediate, approach (intoduced in [9]) abstracting the details on the one hand, while doing justice to the dynamic complexity on the other. Treating a neuron as a heterogeneous ensemble of numerous interacting ion-channel proteins and using statistical mechanics terms, we interpret neuronal response fluctuations and excitability dynamics as reflections of self-organization of the ensemble that resides near a critical point.

11.1 Neuronal Excitability

Cellular excitability is a fundamental physiological process, which plays an important role in the function of many biological systems. An excitable cell produces an all-or-none event, termed action potential (AP), in response to a strong enough (but small compared to the response) perturbation or input. Excitability, as a measurable biophysical property of a membrane, is thus defined as its susceptibility to such a perturbation, or, alternatively, as the minimal input required to generate an AP. In their seminal work, Hodgkin and Huxley [10] have explained the dynamics of the AP and its dependence on various macroscopic conductances of the membrane. In later years, these conductances were shown to result from the collective action of numerous quantized conductance elements, namely proteins functioning as transmembrane ion channels.

Excitability in the Hodgkin-Huxley (HH) model is determined by a set of maximal conductance parameters 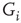c11-math-0007, with 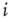c11-math-0008 designating each of the relevant conductances. The effect of these parameters on the excitability of a neuron can be demonstrated by changing the maximal sodium conductance, 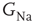c11-math-0009 (Figure 11.1). As the sodium conductance decreases, so does the excitability, as measured by the response threshold, or by the corresponding response latency to a supra-threshold input. For a critically low 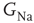c11-math-0010, the neuron becomes unexcitable and stops responding altogether. The existence of a sharp transition between “excitable” and “non-excitable” membrane states is even more pronounced when one looks at the conduction of the AP along a fiber, for example, an axon. Of course, excitability is determined by more than one conductance, and its phase diagram is consequently richer, but the general property holds: the excitable and non-excitable states (or phases) are separated by a sharp boundary in the parameter space.

nfg001

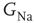Figure 11.1 Excitability in a Hodgkin- Huxley (HH) neuron (adaptaed from [9]). (a) The effect of modulating c11-math-0001 on the voltage response of an isopotential HH neuron to a short (500 μs) current pulse. As c11-math-0002 decreases, the AP is delayed. Below a certain critical conductance, no AP is produced. (b) The effect of modulating 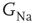c11-math-0003 on the voltage response of an HH axon with 50 compartments expressed at the fiftieth compartment, to a short (500 μs) current pulse given at the first compartment. The delayed latency effect is enhanced (due to reduced conduction velocity), and below the critical level the response is flattened (the subthreshold response is not transmitted from the first to the fiftieth compartment). (c) AP latency in (a) as a function of 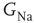c11-math-0004, demonstrating the existence of a sharp threshold. Above-threshold APs are marked with filled circles, and non-AP events are marked with empty circles. (d) AP latency in (b) as a function of c11-math-0005. Shaded area is a regime where no event was propagated. 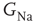(e) The stimulation threshold (minimal current to elicit an AP) is plotted as a function of c11-math-0006 for the fiftieth compartment neuron.

In the short term (about 10 ms) which is accounted for by the HH model, maximal conductances can safely assumed to be constant, justifying the parameterization of 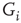c11-math-0011. However, when long-term effects are considered, the maximal conductance can (and indeed should) be treated as a macroscopic system variable governed by stochastic, activity-dependent transitions of ion channels into and out of long-lasting unavailable states (reviewed in [11]). In an unavailable state, ion channels are “out of the game” as far as the short-term dynamics of the AP generation is concerned, and the corresponding values of 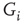c11-math-0012 are effectively reduced. Viewed as such, excitability has the flavor of an order parameter, reflecting population averages of availability of ion channels to participate in the generation of APs. In what follows, we describe a set of observations that characterize the dynamics of excitability over extended durations, and interpret these observations in the framework of SOC.

11.2 Experimental Observations on Excitability Dynamics

In a series of experiments, detailed in a previous publication [8], the intrinsic dynamics of excitability over time scales longer than that of an AP was observed by monitoring the responses of single neurons to series of pulse stimulations. In brief, cortical neurons from newborn rats were cultured on multielectrode arrays, allowing extracellular recording and stimulation for long, practically unlimited, durations. The neurons were isolated from their network by a pharmacological synaptic blockage to allow the study of intrinsic excitability dynamics, with minimal interference by synaptically coupled cells. Neurons were stimulated with sequences of short, identical electrical pulses. For each pulse, the binary response (AP produced or not) was registered, marking the neuron as being either in the excitable or the unexcitable state. For each AP recorded, the latency from stimulation to the AP was also registered, quantifying the neuron's excitability. The amplitude of the stimulating pulses was constant throughout the experiment and well above threshold, such that neurons responded in a 1 : 1 manner (i.e., every stimulation pulse produces an AP) under low rate (1 Hz) stimulation conditions. Various control measures were used to verify experimental stability, see [8] for details.

When the stimulation rate 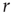c11-math-0014 is increased beyond 1 Hz, and the neuron is allowed to reach a steady-state response, one of two distinct response regimes can be identified: a stable regime, in which each stimulation elicits an AP, and an intermittent regime, in which the spiking is irregular. The response of a neuron following a change of stimulation rate is demonstrated in Figure 11.2, as well as in [8]: When the stimulation rate is abruptly increased, the latency gradually becomes longer and stabilizes at a new, constant value (as is evident in the first two blocks, where the rate is increased to 5 and 7 Hz). For a sufficiently high stimulation rate (above a critical value 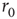c11-math-0015), the 1 : 1 response mode breaks down and becomes intermittent (the 20-Hz block in the example shown). All transitions are fully reversible. The steady-state properties of the two response regimes may be observed by slowly changing the stimulation rate, so its response properties can be safely assumed to reflect an excitability steady state. As seen in the result of the “adiabatic” experiment (Figure 11.3a), the stable regime is characterized by a 1 : 1 response (no failures), stable latency (low jitter), and monotonic dependence of latency on stimulation rate. In contrast, the intermittent regime is characterized by a failure rate that increases with stimulation rate, unstable latency (high jitter), and independence of the mean latency on the stimulation rate. The existence of a critical (or threshold) stimulation rate is reflected in measures of the failure rate (Figure 11.3b), mean latency (Figure 11.3c), and latency coefficient of variation (Figure 11.3d). The exact value of 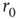c11-math-0016 varies considerably between neurons, but its existence is observed in practically all measured neurons (see details in [8]).

nfg002

Figure 11.2 Experimental study of excitability dynamics. An isolated neuron is stimulated with a sequence of short (400 μs) electrical pulses. Shown are extracellular voltage response traces, each 20 ms long. The traces are ordered from top to bottom, and temporally aligned to the stimulation time. For visual clarity, only every other trace is plotted. In the example shown, the neuron is stimulated with a 1-Hz sequence for 1 min (top section of the figure, 60 traces). For this stimulation protocol, the response latency is stable (arrow shows the time between stimulation and spike) and the response is reliable, implying constant excitability. The stimulation rate is then abruptly increased to 20 Hz for 2 min (middle section). After a transient period, in which latency is gradually increased (excitability decreases), the neuron reaches an intermittent steady state, in which it is barely excitable, spiking failures occur, and the response is irregular. When the stimulation rate is decreased back to 1 Hz (bottom section), the latency (excitability) recovers, and the stable steady-state response is restored.

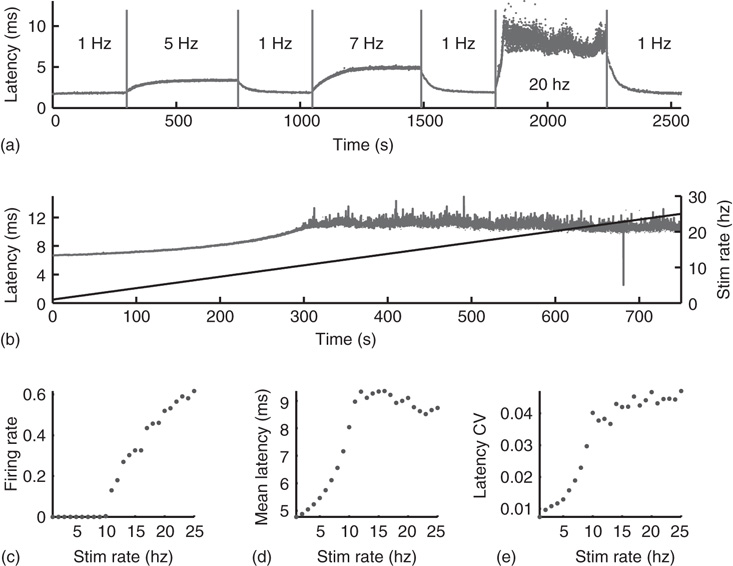
nfg003

Figure 11.3 Steady-state characterization of the response (adaptaed from [9]). (a) The AP latency plotted as a function of time in an experiment where the stimulation rate is changed in an adiabatic manner, meaning slow enough so that the response can be assumed to reflect steady-state properties. For low stimulation rates, the excitability (quantified as the latency from stimulation to AP) stabilizes at a constant above-threshold value (threshold on excitability resources, as exemplified with c11-math-0013 in Figure 11.1). When the stimulation rate is increased, the steady-state excitability is accordingly decreased (latency increased). For high stimulation rates (>10 Hz), excitability reaches the threshold, and the neuron responds intermittently, with strong fluctuations. (b) Response latencies (solid line) in response to a stimulation sequence with slowly increasing stimulation rate (dashed line). (c) Fail (no spike) probability as a function of stimulation rate. A critical stimulation rate is clearly evident. (d) Mean response latency as a function of stimulation rate. The increase of the latency accelerates as the stimulation rate approaches the critical point. (e) The jitter (coefficient of variation) of the latency as a function of the stimulation rate.

Within the intermittent regime, the fluctuations of excitability (as defined by the excitable/unexcitable state sequence) are characterized by scale-free long-memory statistics. Its power spectral density (PSD) exhibits a power law (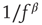c11-math-0018) in the low-frequency range. The characteristic exponent of this power law does not depend on the stimulation rate as long as the latter is kept above c11-math-0019 (Figure 11.4a). 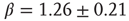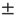The typical exponent of the rate PSD is c11-math-0020 (mean c11-math-0021 SD, calculated over 16 neurons). Moreover, within the intermittent regime, the distributions of the lengths of consecutive response sequences (i.e., periods during which the neuron is fully excitable, responding to each stimulation pulse) and consecutive no-response sequences (periods when the neuron is not responding) are qualitatively different (Figure 11.4b, 11.4c). The consecutive response sequence length histogram is strictly exponential, having a characteristic duration; the consecutive no-response sequence length histogram is wide, to the point of scale-freeness (power law distribution). Likelihood ratio tests for power law distribution fit to the empirical histogram (containing more than 90,000 samples) yielded significantly higher likelihood compared with fits to exponential, log normal, stretched exponential and linear combination of two exponential distributions (normalized log likelihood ratios R>10, p<0.001, see [12]). This suggests that the fluctuations are dominated by widely distributed exculsions into an unexcitable state1. Moreover, as shown in Figure 11.4d, during the intermittent regime, the response of the neuron is characterized by transitions between periods characterized by different typical quasi-stable temporal response patterns that dominate the response sequence. It is important to emphasize that the instability observed in the intermittent regime is activity dependent. Whenever the stimulation stops for a while, allowing the neuron to recover, its response properties return to its original form.

nfg004

Figure 11.4 Scale-free fluctuations in the intermittent regime (adaptaed from [8]). (a) Periodograms of the failure rate fluctuations, at five different stimulation rates above c11-math-0017. (b) Length distribution of spike–response sequences, on a semilogarithmic plot, demonstrating exponential behavior. Example from one neuron stimulated at 20 Hz for 24 h. (c) Length distribution of no-spike response sequences from the same neuron, on a double-logarithmic plot, demonstrating a power-law-like behavior. (d) Pattern modes in binary response sequences. Extracts (approximately 10 min long) from the response pattern of two neurons to long 20-Hz stimulation. A white pixel represents an interval with a spike response, and black represents an interval with no-spike response. The response sequence is wrapped. Spontaneous transitions between distinct temporal pattern modes occur while the neuron is in the intermittent response regime, visible as different textures of the black/white patterns.

11.3 Self-Organized Criticality Interpretation

The above experimental observations are difficult to interpret within the conventional framework of neuronal dynamics, which relies on extensions of the original formalism of the Hodgkin and Huxley approach. Given that the observed dynamics is intrinsic [8], this formalism dictates integration of many processes into a mathematical model, each with its own unique time scale, to allow reconstructing and fitting the complex scale-free dynamics. When the temporal range of the observed phenomena extends over many orders of magnitudes, such an approach yields large intractable models, the conceptual contribution of which is limited. As we have already discussed previously, we suggest here to take a more abstract direction, viewing the neuron in statistical mechanics terms, as a large ensemble of interacting elements. Under this conjecture, the transition between excitable and unexcitable states of the cell is naturally interpreted as a second-order phase transition. This interpretation is further supported by the described experimental results, which exhibit critical-like fluctuations in the barely excitable regime (around the threshold of excitability). Further motivation for this interpretation can be drawn from mathematical analysis of macroscopic, low dimentional models of excitability, which also exhibit critical behavior near the spiking bifurcation point [15, 16].

However, in this picture the control parameter (“temperature”)2 that moves the membrane between excitable and unexcitable phases is elusive. One immediate candidate is the experimental parameter – the stimulation rate. However, in such a scenario one would expect to observe the critical characteristics within a limited range of stimulation rates; higher values of stimulation rate should shut down excitability altogether. Our experimental results show that this is not the case. For example, the experiments show that the response latency (Figure 11.3c) as well as the characteristic exponent of the PSD (Figure 11.4a) are insensitive to the stimulation rate. The reason for this apparent inconsistency is that the stimulation rate does not directly impact the dynamics of the underlying ionic channels. Rather, the relevant control parameter is in fact the activity rate, which itself is a dynamic variable of the system. This is consistent with the known biophysics of ion channels, in which transition rates are dependent on the output of the system – the membrane voltage or neuronal activity. This picture implies that a form of self-organization is at work here.

The concept of SOC [17] designates a cluster of physical phenomena characterizing systems that reside near a phase transition. What makes SOC unique is the fact that residing near a phase transition is not the result of a fine-tuned control parameter; rather, in SOC the system posits itself near a phase transition as a natural consequence of the underlying internal dynamic process that drives toward the critical value. Such systems exhibit many complex statistical and dynamical features that characterize their behavior near a phase transition, without these features being sensitive to system parameters. The most well-known canonical example for such a system is the sandpile model, in which the relevant parameter is the number of its grains (or equivalently, the steepness of its slope). This parameter is characterized by a critical value that separates the stable and unstable phases. However, in the context of SOC sandpile models, this “control” parameter is not externally set but is a dynamical variable of the system. When the system is stable, grains are added onto the pile, and while it is unstable, grains are lost via its margins. The most prominent property of a system in a state of SOC is the avalanche: an episode of instability that propagates through the system, with size and lifetime distributions that follow a power law form.

The sandpile model of Bak, Tang, and Wiesenfeld (BTW) is a cellular automaton with an integer variable 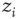c11-math-0022 (“energy”), defined on a finite 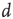c11-math-0023-dimensional lattice. At each time step, an energy grain is added to a randomly chosen site. When the energy of a certain site reaches a threshold 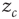c11-math-0024, the site relaxes as 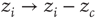c11-math-0025, and the energy is distributed between the nearest neighbors of the active site. This relaxation can induce threshold crossings at the neighboring sites, potentially propagating through the lattice until all sites relax. Grains that “fall off” the boundary are dissipated out of the system. The sequence of events from the initial excitation until full relaxation constitutes an avalanche. The model requires that grain addition will occur only when the system is fully relaxed. Under these conditions, the size and lifetime of the avalanches will follow a power law distribution, and order parameters such as the total energy in the pile will fluctuate with a 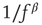c11-math-0026 spectral density.

The BTW model, as well as its later variants, is nonlocal in the sense that events in a certain point in the lattice (grain addition) depend on the state of the entire lattice (full relaxation). Dickman, Vespignani and Zapperi [18, 19] have shown that this model can be made to conform to the “conventional” phase-transition model by introducing periodic boundary conditions (thereby preventing dissipation) and stopping the influx of grains, while retaining the local dynamic rule of the original model. In such a model, the number of grains in the pile is conserved and serves as the relevant control parameter. This model is known as the activated random walk model: walkers (or grains) are moved to adjacent cells if they are pushed by another walker (in the version with 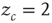c11-math-0027), otherwise they are paralyzed. This is an example of a model with an absorbing state (AS): if all walkers are inactive (i.e., none is above threshold), the dynamics of the model freezes. When the number of walkers on the lattice is low, the model is guaranteed to reach an AS within a finite time. If, on the other hand, the number of walkers is high, the probability of reaching the AS becomes so low that the expected time to reach it becomes infinite. The transition between the two phases is a second-order phase transition. In the sandpile model, the number of walkers on the lattice becomes a dynamic variable of the system, with a carefully designed dynamics: as long as the system is super-critical, with constantly moving walkers, grains will keep on falling off the edge of the pile, until an absorbing state will be reached. Once the pile is quiescent, new grains will be added. In such a way, the number of grains is guaranteed to converge to the critical value. Dickman et al. [18, 19] have shown that many of the popular SOC models can be viewed as an AS model with a feedback from the system state onto the control parameter, which effectively pushes it to the critical value.

This picture intuitively maps excitability dynamics, where neural activity serves as a temperature-like parameter, and the single AP serves as a drive (quantal influx of energy, or small increase in temperature). In the absence of activity, the neuron reaches an excitable phase, while increased activity reduces excitability, and (when high enough) pushes the membrane into the unexcitable phase. While the system is in the unexcitable phase, neural activity is decreased, leading to restoration of excitability. As a result, the neuron resides in a state where it is “barely excitable,” exhibiting characteristics of SOC. Of course, not all classes of neurons follow this simple process, but the general idea holds: activity pushes excitability toward a threshold state, while the longer time scale regulatory feedback reigns in the system.

11.4 Adaptive Rates and Contact Processes

This interpretation of excitability in SOC terms may also be theoretically supported, within certain limits, by considering the underlying biophysical machinery. The state of the membrane is a function of the individual states of a large population of interacting ion-channel proteins. A single ion channel can undergo transformations between uniquely defined conformations, which are conventionally modeled as states in a Markov chain. The faster transition dynamics between states is the foundation of the HH model, which describes the excitation event itself – the AP. But, as explained previously, for the purpose of modeling the dynamics of excitability, rather than the generative dynamics of the AP itself, it is useful to group these conformations into two sets [11, 20–22]: the available, in which channels can participate in generation of APs, and the unavailable, in which channels are deeply inactivated and are “out of the game” of AP generation. The microscopic details of the single-channel dynamics in this state space, and definitely the collective dynamics of the interacting ensemble, are complex [13, 20] and no satisfactory comprehensive model exists to date. There are several approaches for modeling channel dynamics, the most widespread is the Markov chain approach, in which a channel moves in a space of conformations, with topology and parameters fitted to experimental observations. Such a model can, in general, be very large, containing many states and many parameters [14, 21]. Another approach advocates a more compact representation, mostly containing functionally defined states, but with dynamics that are non-Markovian, meaning that transition probabilities can be history-dependent [13, 23, 24]. These two approaches are focused on the single-channel dynamics. However, it has been suggested recently [11, 22] that the transition dynamics between the available and unavailable states may be expressed in terms of an “adaptive rate” logistic-function-like model of the general form

11.1 equation

where f is a function of the neural activity measure γ, and g(x) is a monotonically increasing function of the system state x.

Following the lead of the above adaptive rate approach, one can consider, for instance, a model in which 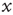c11-math-0029 represents the availability of a restoring (e.g., potassium) conductance.3 The state of the single channel is represented by a binary variable 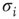c11-math-0030, where 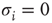c11-math-0031 is the unavailable state and 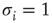c11-math-0032 is the available state. Unavailable channels are recruited with a rate of 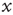c11-math-0033, while available channels are lost with a rate of 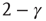c11-math-0034. This picture gives rise to a dynamical mean-field-like equation

11.2 equation

The model is a variant of a globally coupled contact process, which is a well-studied system exhibiting an AS phase transition [26]. Here, 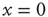c11-math-0036 is the AS, representing the excitable state of the system. In the artificial case of taking 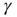c11-math-0037 as an externally modified control parameter, for 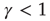c11-math-0038 (low activity) the system will always settle into this state, and the neuron will sustain this level of activity. For 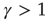c11-math-0039, the system will settle on 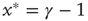c11-math-0040, which is an unexcitable state, and the neuron will not be able to sustain activity. Feedback is introduced into the system by specifying the state dependency of 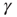c11-math-0041: An AP is fired if and only if the system is excitable (i.e., in the absence of restoring conductance, 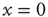c11-math-0042), giving rise to a small increase in 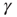c11-math-0043. When 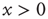c11-math-0044, the system is unexcitable, APs are not fired, and 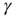c11-math-0045 is slowly decreased. This is an exact implementation of the scheme proposed in Dickman et al. [18, 19]: an absorbing state system, where the control parameter (activity, 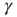c11-math-0046) is modified by a feedback from the order parameter (excitability, a function of 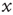c11-math-0047). As always with SOC, the distinction between order and control parameters becomes clear only when the conservative, open-loop version of the model is considered.

Note that the natural dependency of the driving event (the AP) on the system state in our neural context resolves a subtlety involved in SOC dynamics: the system must be driven slowly enough to allow the AS to be reached before a new quantum of energy is invested. In most models, this condition is met by assuming the rate to be infinitesimally small.

Numerical simulation of the model (Eq. 11.2), together with the closed-loop dynamics of 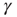c11-math-0055, qualitatively reproduces the power law statistics observed in the experiment, including the existence of a critical stimulation rate 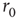c11-math-0056 (Figure 11.5a), the 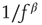c11-math-0057 behavior for 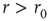c11-math-0058, with exponent independent of 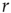c11-math-0059 (Figure 11.5b), and the distributions of sequence durations (Figures 11.5c and 11.5D). The critical stimulation rate 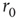c11-math-0060 is adjustable by the kinetics of 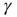c11-math-0061, its increase and decrease during times of activity, and inactivity of the neuron. While this simplistic model does capture the key observed properties, others are not accounted for. The latency transient dynamics when switching between stimulation rates (Figure 11.2b) and the multitude of stable latency values for 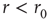c11-math-0062 (Figure 11.3) suggest that a model with a single excitable state is not sufficient. Sandpile models (and more generally activated random walk models, see Dickman et al. [18, 19]) do exhibit such multiplicity, arising out of a continuum of stable subcritical values of pile height (or slope). In this analogy, adding grains to the pile increases its height up to the critical point, where SOC is observed. Another experimentally observed property that is not accounted for by the model is the existence of pattern modes in the intermittent response regime as described in Figure 11.4d, implying temporal correlations between events of excitability and unexcitability. Also, the fact that the 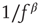c11-math-0063 relation of the PSD extends to a time scale much longer than the maximal avalanche duration suggests that these correlations have a significant contribution for the observed temporal dynamics. While such correlations and temporal patterns can be generated in SOC models [27] and while they characterize the dynamics in other (non-self-organizing) critical systems, they are still largely unexplored.

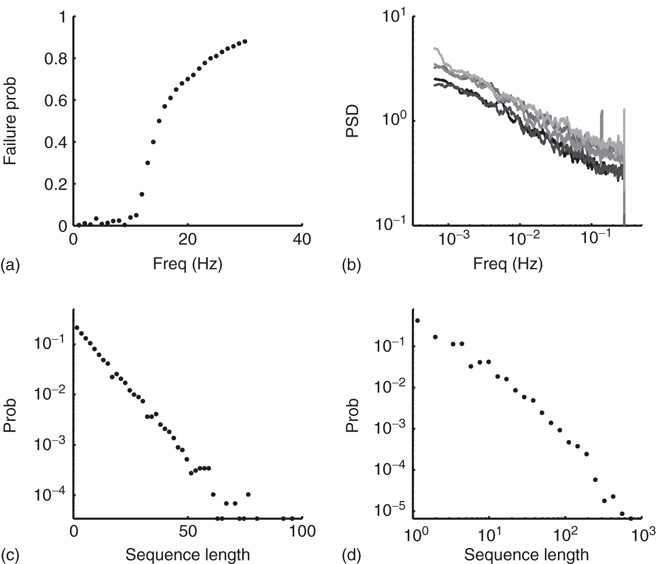
nfg005

Figure 11.5 Model simulation results (adaptaed from [9]). All simulations were performed using an ensemble of 10 000 channels. The loop on neuronal activity 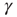c11-math-0048 was closed as follows: for each AP fired, a single channel was inactivated, and 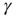c11-math-0049 was increased by a value of 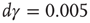c11-math-0050. Between APs, 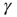c11-math-0051 decayed exponentially with a rate of 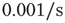c11-math-0052. (a) Dependence of the spike failure probability on the stimulation rate, analogous to Figure 11.3b. Each point in the graph was estimated from 1-h simulated time. (b) Power spectral densities of the response fluctuations at different frequencies above 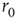c11-math-0053. Each PSD was computed from a period of 12 h of simulated time. (c) Length distribution of spike–response sequences, on a semilogarithmic plot, demonstrating an exponential behavior. Analogous to Figure 11.4b. The distribution was estimated from 24-h simulated time, with stimulation at a constant, above 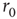c11-math-0054, stimulation rate. (d) Length distribution of no-spike response sequences from the same neuron, on a double-logarithmic plot, demonstrating a power-law-like behavior. Analogous to Figure 11.4c.

11.5 Concluding Remarks

In this chapter, we have focused on SOC as a possible framework to account for temporal complexity in neuronal response variations. The motivation for this approach stems from the macroscopic behavior of the neuron in the experiments of Gal et al. [8], which can be mapped to the macroscopic behavior of many models exhibiting SOC. In the neuron, excitability is slowly reduced from the initial level as a result of activity; this reduction continues until excitability drops below a threshold level, leading to a pause in activity. Excitability is then restored following an avalanche-like period of unexcitability, and so forth. For comparison, in the canonical SOC model of the sandpile, grains are added continuously to the top of the pile. The pile's height and slope slowly increase until they reach a critical level, where the pile loses stability. Stability is then restored by an avalanche, which decreases the slope back to a subcritical level, from where the process starts again. This analogy is supported by the critical-like behavior of excitability fluctuations around its threshold.

In addition to the macroscopic behavior, we have offered a microscopic “toy model,” based on known ion-channel dynamics, that might reproduce this behavior. This model is built upon an approach called adaptive rates [11, 22], accounting for the observed dynamics of ion channels by introducing an ensemble-level interaction term. We have shown how variants of this general scheme might result in formal SOC. It is important to stress, however, that the instantiation used here is not unique, and is not intended to represent any specific ion channel. It is merely a demonstration that the emergence of the self-organized critical behavior is not alien to theoretical formulations of excitability. This said, candidate ionic channels with similar properties to those used in the model do exist. For example, the calcium-dependent potassium SK channel [25] is an excitability inhibitor, which has a calcium-mediated positive interaction, not unlike the one used in the model suggested here. Also, note that the formulation chosen here does not give rise to an exact reproduction of the observed phenomenology. Not only do the exponents of the critical behavior not match (in the language of critical phenomena this means that the experiment and the model are not in the same universality class), but the model family used here produces uncorrelated avalanche sizes, while in the experiments the response breaks are clearly correlated and form complex patterns and distinct quasi-stable patterns. However, this is not a general property of critical behavior, and other models (e.g., [27]) can produce correlated, complex temporal patterns.

As attractive as the SOC interpretation might be, it is acknowledged that this framework is highly controversial. Many physicists question the relevance of this approach to the natural world, and in spite of the many candidate phenomena that have been suggested as reflecting SOC (e.g., forest fires, earthquakes, and, of course, pile phenomena such as sand and snow avalanches), no sound models have been suggested to account for these phenomena to date. One of the obstacles is the subtlety inherent to the involved feedback loop, because the driving of the model must depend on its state. In the case of excitability, this loop seems natural: the occurrence of an AP is directly dependent on the macroscopic state of the membrane – its excitability.

The mapping between SOC and excitability suggested here is only a first step, which can be regarded as an instigation of a research program. This program should include both experimental and theoretical efforts, to support and validate the SOC interpretation in the context of neuronal excitability. Specific issues should be addressed: First, is the transition of the membrane between the excitable and the unexcitable states a genuine second-order phase transition? Ideally, this question should be addressed using carefully designed experiments that enable investigation of the approach to the transition point, from both sides. Care must be taken to define and manipulate the excitability of the neuron (the relevant control parameter). This can be achieved, for example, by the well-controlled application of channel blockers (e.g., tetrodotoxin, charybdotoxin), which have a direct impact on excitability (Figure 11.1). Second, the existence of this phase transition should also be demonstrated by manipulating the neuronal level of activity. A possibly useful technique here is the so-called response clamp method, recently introduced by Wallach and colleagues [28, 29], which clamps neuronal activity to a desired level by controlling stimulation parameters. Third, careful characterization of the critical phenomena around this phase transition should be made, in order to point to plausible theoretical models. It should be emphasized that these suggested experiments are in a regime where the feedback loop of the SOC is broken, by enforcing fixed excitability/activity levels. On the theoretical side, the space of possible models should be explored, portraying the scope of phenomena accountable by SOC, and hopefully should converge on a biophysical plausible model that reproduces as much of the observed data as possible. Finally, the ultimate challenge for SOC is for it to account for aspects of neuronal dynamics beyond critical statistics (with the usual power law characteristics), with emphasis on functional aspects.

SOC constitutes one hardly explored framework for understanding response fluctuations in single neurons. It can be considered as a niche inside the larger class of stochastic modeling. Such models can lead to temporal complexity in compact formalisms with several possible stochastic mechanisms (e.g., [6, 21, 23]). A further theoretical investigation of these modeling approaches might provide useful representations of temporal complexity in neurons, other than SOC. Such an investigation was recently carried out by Soudry and Meir, [30, 31]. They conducted a study that draws the boundaries for the range of phenomena that may be generated by conductance-based stochastic models (i.e., with channel noise) and discusses the extent to which such models can explain the data presented here. Deterministic chaotic models are also an attractive paradigm that is able to generate temporal complexity, and was explored in several past studies (for review see [32, 33]).

Self-organization is an important concept in the understanding of biological systems, including the study of excitable systems. Many studies have demonstrated how excitability is “self-organized” into preferable working points following perturbations or change in conditions [34–39]. These and related phenomena are conventionally classified under homeostasis, and are shown to depend on mechanisms such as calcium dynamics or ion channel inactivation. While a connection between SOC and activity homeostasis was hypothesized in the context of a neural network [40], it still awaits extensive explorations, both theoretically and experimentally.

In summary, we provided several arguments, experimental and theoretical, in support of a plausible connection between the framework of SOC and the dynamics underlying response fluctuations in single neurons. This interpretation succeeds in explaining critical-like fluctuations of neuronal responsiveness over extended time scales, which are not accounted for by other more common approaches. Acknowledging the limitations of the simplified approach presented here, and respecting the gap between theoretical models and biological reality, we submit that SOC seems to capture the core phenomenology of fluctuating neuronal excitability, and has a potential to enhance our understanding of physiological aspects of excitability dynamics.

References

  1. 1. Beggs, J.M. and Plenz, D. (2003) Neuronal avalanches in neocortical circuits. J. Neurosci., 23 (35), 11 167.
  2. 2. Chialvo, D. (2010) Emergent complex neural dynamics. Nat. Phys., 6 (10), 744–750.
  3. 3. Beggs, J.M. and Timme, N. (2012) Being critical of criticality in the brain. Front. Physiol., 3, 163, doi: 10.3389/fphys.2012.00163. http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=336%9250&tool=pmcentrez&rendertype=abstract (accessed 10 December 2013).
  4. 4. Lowen, S.B. and Teich, M.C. (1996) The periodogram and Allan variance reveal fractal exponents greater than unity in auditory-nerve spike trains. J. Acoust. Soc. Am., 99 (6), 3585–3591.
  5. 5. Teich, M.C., Heneghan, C., Lowen, S.B., Ozaki, T., and Kaplan, E. (1997) Fractal character of the neural spike train in the visual system of the cat. J. Opt. Soc. Am. A, 14 (3), 529–546.
  6. 6. Soen, Y. and Braun, E. (2000) Scale-invariant fluctuations at different levels of organization in developing heart cell networks. Phys. Rev. E, 61 (3), R2216-R22-9.
  7. 7. Lowen, S.B., Ozaki, T., Kaplan, E., Saleh, B.E., and Teich, M.C. (2001) Fractal features of dark, maintained, and driven neural discharges in the cat visual system. Methods, 24 (4), 377–394. doi: 10.1006/meth.2001.1207.
  8. 8. Gal, A., Eytan, D., Wallach, A., Sandler, M., Schiller, J., and Marom, S. (2010) Dynamics of excitability over extended timescales in cultured cortical neurons. J. Neurosci., 30 (48), 16-332-16-342, doi: 10.1523/JNEUROSCI.4859-10.2010. http://www.ncbi.nlm.nih.gov/pubmed/21123579; http://www.jneurosci.org/cgi/content/abstract/30/48/16332 (accessed 10 December 2013).
  9. 9. Gal, A. and Marom, S. (2013). Self-organized criticality in single-neuron excitability. Physical Review E, 88 (6), 062717. doi:10.1103/PhysRevE.88.062717.
  10. 10. Hodgkin, A. and Huxley, A. (1952) A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol., 117, 500–544.
  11. 11. Marom, S. (2010) Neural timescales or lack thereof. Prog. Neurobiol., 90 (1), 16–28, doi: 10.1016/j.pneurobio.2009.10.003. http://www.ncbi.nlm.nih.gov/pubmed/19836433 (accessed 10 December 2013).
  12. 12. Clauset, A., Shalizi, C.R., and Newman, M.E.J. (2009) Power-law distributions in empirical data. SIAM Review.
  13. 13. Liebovitch, L.S., Fischbarg, J., Koniarek, J.P., Todorova, I., and Wang, M. (1987) Fractal model of ion-channel kinetics. Biochim. Biophys. Acta, 896 (2), 173–180, doi: 10.1016/0005-2736(87)90177-5. http://dx.doi.org/10.1016/0005-2736(87)90177-5.
  14. 14. Millhauser, G.L., Salpeter, E.E., and Oswald, R.E. (1988) Diffusion models of ion-channel gating and the origin of power-law distributions from single-channel recording. Proc. Natl. Acad. Sci. U.S.A., 85 (5), 1503-1507, http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=279%800&tool=pmcentrez&rendertype=abstract (accessed 10 December 2013).
  15. 15. Roa, M., Copelli, M., Kinouchi, O., and Caticha, N. (2007) Scaling law for the transient behavior of type-II neuron models. Physical Review E, 75 (2), 021911, doi:10.1103/PhysRevE.75.021911.
  16. 16. Steyn-Ross, D., Steyn-Ross, M., Wilson, M., and Sleigh, J. (2006) White-noise susceptibility and critical slowing in neurons near spiking threshold. Physical Review E, 74 (5), 051920, doi:10.1103/PhysRevE.74.051920.
  17. 17. Bak, P., Tang, C., and Wiesenfeld, K. (1987) Self-organized criticality: an explanation of 1/f noise. Phys. Rev. Lett., 59 (4), 381–384.
  18. 18. Dickman, R., Vespignani, A., and Zapperi, S. (1998) Self-organized criticality as an absorbing-state phase transition. Phys. Rev. E, 57 (5), 5095–5105, doi: 10.1103/PhysRevE.57.5095. http://pre.aps.org/abstract/PRE/v57/i5/p5095_1 (accessed 10 December 2013).
  19. 19. Dickman, R., Muñoz, M., Vespignani, A., and Zapperi, S. (2000) Paths to self-organized criticality. Braz. J. Phys., 30 (1), 27-41, http://www.scielo.br/scielo.php?pid=S0103-97332000000100004&%script=sci_arttext (accessed 10 December 2013).
  20. 20. Toib, A., Lyakhov, V., and Marom, S. (1998) Interaction between duration of activity and time course of recovery from slow inactivation in mammalian brain Na+ channels. J. Neurosci., 18 (5), 1893–1903.
  21. 21. Gilboa, G., Chen, R., and Brenner, N. (2005) History-dependent multiple-time-scale dynamics in a single-neuron model. J. Neurosci., 25 (28), 6479–6489, doi: 10.1523/JNEUROSCI.0763-05.2005.
  22. 22. Marom, S. (2009) Adaptive transition rates in excitable membranes. Front. Comput. Neurosci., 3, 2. doi: 10.3389/neuro.10.002.2009.
  23. 23. Lowen, S.B., Liebovitch, L.S., and White, J.A. (1999) Fractal ion-channel behavior generates fractal firing patterns in neuronal models. Phys. Rev. E, 59 (5 Pt B), 5970–5980.
  24. 24. Soudry, D. and Meir, R. (2010) History-dependent dynamics in a generic model of ion channels - an analytic study. Front. Comput. Neurosci., 4, 1–19, doi: 10.3389/fncom.2010.00003. http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=291%6672&tool=pmcentrez&rendertype=abstract (accessed 10 December 2013).
  25. 25. Adelman, J.P., Maylie, J., and Sah, P. (2012) Small-conductance Ca2+-activated K+ channels: form and function. Annu. Rev. Physiol., 74, 245–69, doi: 10.1146/annurev-physiol-020911-153336. http://www.ncbi.nlm.nih.gov/pubmed/21942705 (accessed 10 December 2013).
  26. 26. Harris, T. (1974) Contact interactions on a lattice. Ann. Probab., 2 (6), 969–988, http://www.jstor.org/stable/10.2307/2959099 (accessed 10 December 2013).
  27. 27. Davidsen, J. and Paczuski, M. (2002) Noise from correlations between avalanches in self-organized criticality. Phys. Rev. E, 66 (5), 050 101, 1/F doi: 10.1103/PhysRevE.66.050101. http://link.aps.org/doi/10.1103/PhysRevE.66.050101 (accessed 10 December 2013).
  28. 28. Wallach, A., Eytan, D., Gal, A., Zrenner, C., and Marom, S. (2011) Neuronal response clamp. Front. Neuroeng., 4, 3. doi: 10.3389/fneng.2011.00003. http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=307%8750&tool=pmcentrez&rendertype=abstract (accessed 10 December 2013).
  29. 29. Wallach, A. (2013) The response clamp: functional characterization of neural systems using closed-loop control. Front. Neural Circ., 7, 5, doi: 10.3389/fncir.2013.00005. http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=355%8724&tool=pmcentrez&rendertype=abstract (accessed 10 December 2013).
  30. 30. Soudry, D. and Meir, R. (2012) Conductance-based neuron models and the slow dynamics of excitability. Front. Comput. Neurosci., 6, 4, doi: 10.3389/fncom.2012.00004. http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=328%0430&tool=pmcentrez&rendertype=abstract (accessed 10 December 2013).
  31. 31. Soudry, D. and Meir, R. (2013) The neuron's response at extended timescales. arXiv preprint arXiv:1301.2631
  32. 32. Korn, H. and Faure, P. (2003) Is there chaos in the brain? II. Experimental evidence and related models. C. R. Biol., 326 (9), 787–840, doi: 10.1016/j.crvi.2003.09.011. http://linkinghub.elsevier.com/retrieve/pii/S1631069103002002% (accessed 10 December 2013).
  33. 33. Faure, P. and Korn, H. (2001) Is there chaos in the brain? I. Concepts of nonlinear dynamics and methods of investigation. C. R. Acad. Sci. Sér. III, Sci., 324 (9), 773–93, http://www.ncbi.nlm.nih.gov/pubmed/11558325 (accessed 10 December 2013).
  34. 34. Prinz, Aa., Billimoria, C.P., and Marder, E. (2003) Alternative to hand-tuning conductance-based models: construction and analysis of databases of model neurons. J. Neurophysiol., 90 (6), 3998–4015, doi: 10.1152/jn.00641.2003. http://www.ncbi.nlm.nih.gov/pubmed/12944532 (accessed 10 December 2013).
  35. 35. Turrigiano, G., Abbott, L.F., and Marder, E. (1994) Activity-dependent changes in the intrinsic properties of cultured neurons. Science, 264 (5161), 974–977, http://www.sciencemag.org/content/264/5161/974.short (accessed 10 December 2013).
  36. 36. LeMasson, G., Marder, E., and Abbott, L.F. (1993) Activity-dependent regulation of conductances in model neurons. Science, 259 (5103), 1915–1917.
  37. 37. Liu, Z., Golowasch, J., Marder, E., and Abbott, L.F. (1998) A model neuron with activity-dependent conductances regulated by multiple calcium sensors. J. Neurosci., 18 (7), 2309–2320.
  38. 38. Marom, S., Toib, A., and Braun, E. (1995) Rich dynamics in a simplified excitable system. Adv. Exp. Med. Biol., 382, 61–66.
  39. 39. Kispersky, T.J., Caplan, J.S., and Marder, E. (2012) Increase in sodium conductance decreases firing rate and gain in model neurons. J. Neurosci., 32 (32), 10–995-10-1004. doi: 10.1523/JNEUROSCI.2045-12.2012. http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=342%7781&tool=pmcentrez&rendertype=abstract (accessed 10 December 2013).
  40. 40. Hsu, D. and Beggs, J.M. (2006) Neuronal avalanches and criticality: a dynamical model for homeostasis. Neurocomputing, 69 (10-12), 1134–1136, doi: 10.1016/j.neucom.2005.12.060. http://dx.doi.org/10.1016/j.neucom.2005.12.060.