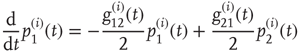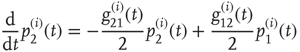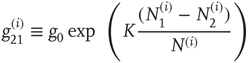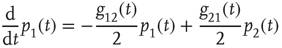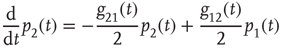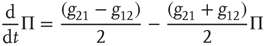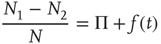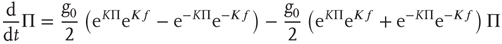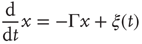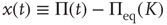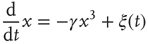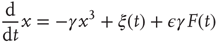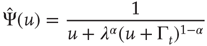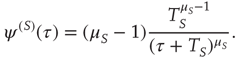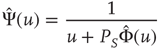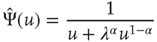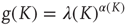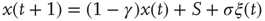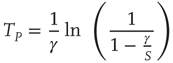23
Neural Dynamics: Criticality, Cooperation, Avalanches, and Entrainment between Complex Networks
23.1 Introduction
The discovery of avalanches in neural systems [1] has aroused substantial interest among neurophysiologists and, more generally, among researchers in complex networks [2–4] as well. The main purpose of this chapter is to provide evidence in support of the hypothesis that the phenomenon of neural avalanches [1] is generated by the same cooperative properties as those responsible for a surprising effect which we call cooperation-induced (CI) synchronization, illustrated in [5]. The phenomenon of neural entrainment [6] is another manifestation of the same cooperative property. We also address the important issue of the connection between neural avalanches and criticality. Avalanches are thought to be a manifestation of criticality, and especially self-organized criticality [7, 8]. At the same time, criticality is accompanied by long-range correlation [7], and a plausible model for neural dynamics is expected to account for the astounding interaction between agents separated by relatively large distances. General agreement exists in the literature that brain function rests on these crucial properties, and the phase-transition theory for physical phenomena [9] is thought to afford the most important theoretical direction for further research work on this subject. In this theory, criticality emerges at a specific single value of a control parameter, designated by the symbol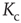 
. In this chapter, we illustrate a theoretical model generating avalanches, long-range correlation, and entrainment, as a form of CI synchronization, over a wide range of values of the control parameter 
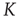, thereby suggesting that the form of criticality within the brain is not the ordinary criticality of physical phase transitions but is instead the extended criticality recently introduced by Longo and coworkers [10, 11] to explain biological processes.
Cooperation is the common effort of the elements of a network for their mutual benefit. We use the term cooperation in the same loose sense as that adopted, for instance, by Montroll [12] to shed light on the equilibrium condition realized by the interacting spins of the Ising model. Although the term cooperation, frequently used in this chapter, does not imply a network's cognition, we follow the conceptual perspective advocated by Werner [13] that cognition emerges at criticality, with the proviso that its cause may be extended criticality (EC).
The term cooperation suggests a form of awareness that these units do not have and must be used with caution especially because in this chapter we move from an Ising-like model to a model of interacting neurons that seems to reproduce certain experimental observations on neural networks which are thought to reflect important properties of brain dynamics, including the emergence of cognition. This is done along the lines advocated by Werner [13], who argues that consciousness is a phenomenon of statistical physics resting on renormalization group theory (RGT) [14]. We afford additional support to this perspective, while suggesting that the form of criticality from which cognition emerges may be more complex than renormalization group criticality, thereby requiring an extension of this theory. All this must be carried out keeping in mind Werner's warning [15] against the use of metaphors of computation and information, which would contaminate the observation with meanings from the observer's mind.
We move from an Ising-like cooperative model to one of interacting neurons, which, although highly idealized, serves very well the purpose of illustrating the cooperative-induced temporal complexity of neural networks. The reason to spend time with the Ising-like cooperative model, discussed in this volume by West et al. [5], is the fact that dealing first with this model clarifies the difference between ordinary criticality, shared with this earlier model, and EC.
The Ising-like model that we adopt is the decision-making model (DMM) that has been used to explain the scale-free distribution of neural links recently revealed by the functional magnetic resonance imaging (fMRI) analysis of the brain [16, 17]. We examine two different weak perturbation conditions: (i) all the units are perturbed by an external low-intensity stimulus, and (ii) a small number of units are perturbed by an external field of large intensity. We show that the response of this cooperative network to extremely weak stimuli, case (i), departs from the predictions of traditional linear response theory (LRT) originally established by Green [18] and Kubo [19] and widely applied by physicists for almost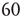 
years. This deviation arises because cooperation generates phase-transition criticality and, at the same time, generates non-ergodic fluctuations, whereas the traditional LRT is confined to the condition of ergodic fluctuations. Condition (ii) is the source of another surprising property: although a few units are strongly perturbed, thanks to cooperation, the stimulus affects the whole network,making that response depart from either ergodic or non-ergodic LRT, thereby generating what we call cooperation-induced (CI) response. This form of response is the source of the perfect synchronization between a complex network and the perturbing stimulus generated by another complex network, a new phenomenon discovered by Turalska et al. [20], whose cooperative origin is illustrated in detail in this chapter. We term this effect CI synchronization. Condition (i) yields the non-ergodic extension of stochastic resonance, and the CI synchronization of condition (ii) is the cooperative counterpart of chaos synchronization.
The second step of our approach to understanding neural complexity and neural avalanches [21] rests on an integrate-and- fire model [22], where the firing of one unit of a set of linked neurons facilitates the firing of the other units. We refer to this model as neural firing cooperation (NFC). We find that, in the case where cooperation is established through NFC, the emerging form of criticality is significantly different from that of an ordinary phase transition. In the typical case of a phase transition, temporal complexity is limited to a singular value of the control parameter, namely of the cooperation strength in the cases examined in this chapter. The NFC cooperation generates temporal complexity analogous to that generated by the DMM, but this temporal complexity, rather than being limited to a single value of the cooperation parameter, is extended to a finite interval of critical values. As a consequence, the new ways of responding to external stimuli are not limited to a singular value of the cooperation parameter either, but their regime of validity is significantly extended, suggesting this to be a manifestation of the new form of criticality which Longo and coworkers [10, 11] call extended criticality (EC). Adopting the EC perspective, we move within the extended critical range, from smaller to larger values of the cooperation parameter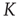 
, and we find that neural avalanches [21] emerge at the cooperation level, making the system adopt the CI response. When a neural network is driven by another neural network with the same complexity, we expect that the response of the perturbed network obeys the new phenomenon of CI synchronization. We notice that these theoretical predictions, of a close connection to neural avalanches and network entrainment, can be checked experimentally through methods of the kind successfully adopted in the University of North Texas laboratory of Gross et al. [23].
Finally, although the emergence of consciousness remains a mystery, we note that the assignment of cognition properties to cooperation [24] leads to temporal complexity with the same power law index as that revealed by the experimental observation of active cognition [25], thereby supporting the conjecture [14] that a close connection between cognition in action and a special form of temporal complexity exists.
The connection between neural cooperation and cognition is certainly far beyond our current understanding of emerging consciousness. Therefore, we limit ourselves to showing that the cooperation between units generates global properties, some of which are qualitatively similar to those revealed by recent analysis of the humanbrain.
23.2 Decision-Making Model (DMM) at Criticality
The DMM [20] is the Ising-like version of an earlier model [26] of a dynamic complex network. The DMM is based on the cooperative interaction of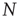 
units, each of which is described by the master equation
where
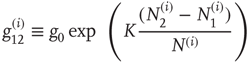
and
The symbol 
denotes the number of nodes linked to the 
th node, with 
and 
being those in the first and second state, respectively. Of course,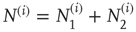 
.
The index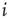 
runs from 
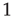to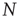 
, where 
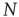is the total number of nodes of the complex network under study, thereby implying that we have to compute 
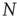pairs of equations of the kind of Eqs. (23.1) and (23.2) at each time step. The adoption of an all-to-all (ATA) coupling condition allows us to simplify the problem. In fact, in that case, all the 
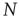pairs of equations are identical to
with
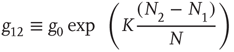
and
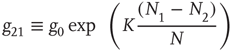
Since normalization requires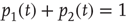 
, it is convenient to replace the pair of equations (23.5) and (23.6) with a single equation for the difference in probabilities:
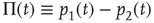
which, after some simple algebra, becomes
It is important to stress that the equality
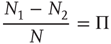
holds true only in the limiting case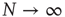 
. In the case of a finite network, 
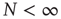, the mean field fluctuates in time, forcing us to adopt
where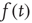 
is a random fluctuation, which according to the law of large numbers has an intensity proportional to 
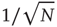. Inserting Eq. (23.12) into Eq. (23.10) yields
and in the limiting case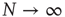 
, the fluctuations vanish, 
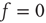, so that Eq. (23.13) generates the well-known phase-transition prediction at the critical value of the control parameter
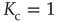
Figure 23.1 shows that, for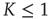 
, the mean field has only one possible equilibrium value, 
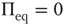. At the critical point 
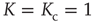, this vanishing equilibrium value splits into two opposite components, one positive and one negative. To understand the important role of criticality, we notice that a finite number of units generates the fluctuation 
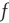, and this, in turn, forces fluctuations in the mean field. At criticality, the fluctuations induced in 
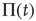have a relatively extended range of free evolution, as made clear in Figure 23.1. In fact, the separation between the two repulsive walls is greatest at criticality. In between them, a free diffusion regime occurs. The supercritical condition 
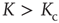generates a barrier of higher and higher intensity with the increase of 
. At the same time, the widths of the two wells shrink, bounding the free evolution regime of the fluctuating mean field to a smaller region.
Figure 23.1 (a) The equilibrium mean field for different values of the cooperation parameter 
. A bifurcation occurs at the critical point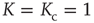 
. (b) Potential barriers for 
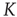subcritical (dashed line, 
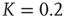), critical (solid line, 
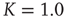), and supercritical (dotted line, 
).
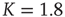23.2.1 Intermittency
Considering a large but finite number of units and expanding Eq. (23.13) to the lowest order contributions of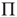 
and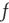 
, it is straightforward to prove that, for either 
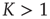or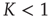 
, due to conditions illustrated in Figure 23.1, the mean field fluctuations are driven by an ordinary Langevin equation of the form
Note that, when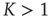 
where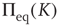 
denotes the equilibrium value for 
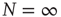. Of course, either at criticality or in the subcritical condition 
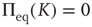, thereby making 
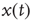coincide with 
.
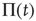At the critical point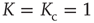 
, we find the time evolution of the mean field to be described by a nonlinear Langevin equation of the form
The linear term that dominates in Eq. (23.15) vanishes identically, and the cooperation between units at criticality displays a remarkable change in behavior, which is characterized by the weakly repulsive walls of Fig. 23.1.
If we interpret the conditions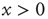 
and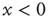 
as corresponding to the light and dark states of blinking quantum dots [27], the DMM provides a satisfactory theoretical representation of this complex intermittent process. It was, in fact, noticed [27] that, if the survival probability 
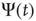, namely the probability that a given state, either light or dark, survives for a time 
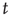after its birth, is evaluated beginning its observation at a time distance 
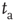from its birth, then its decay becomes slower (aging). Furthermore, this aging effect is not affected by randomly time-ordering the sequence of light and dark states. Notice that the aged curves of Figure 23.2 are actually doublets of survival probabilities generated by shuffled and non-shuffled sequences of states, thereby confirming the renewal nature of this process.
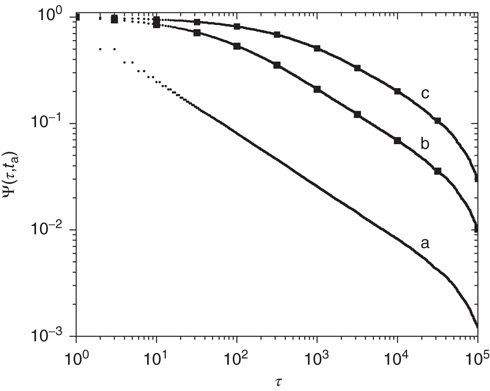
Figure 23.2 The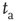 
-aged survival probability of the mean field fluctuations 
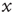at criticality 
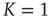for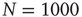 
units and 
. (a)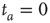 
, the power index 
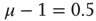. (b) 
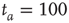. (c)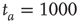 
. The squares in (b) and (c) correspond to the 
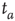-aged survival probability of randomly shuffled sequences of waiting times. Their equivalence to the non-shuffled aged survival probability indicates the fluctuations are renewal.
Figure 23.2 shows that the inverse power law region of the survival probability, corresponding to an inverse power law waiting-time distribution density with power law index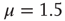 
, has a limited time range of validity. This limitation arises because Eq. (23.17) has an equilibrium distribution, generated by the confining action of the friction term. Thus, the upper time limit of the inverse power law waiting time distribution density is determined by the relation 
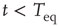, with
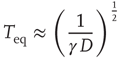
where the diffusion coefficient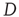 
is proportional to 
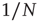. This theoretical prediction is obtained by means of straightforward dimensional arguments [28].
Notice that, in the traditional case of the ordinary Langevin equation, the restoring term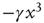 
of Eq. (23.17) is replaced by 
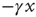and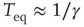 
, implying that at criticality the transient regime is 
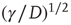times larger than the conventional transition to equilibrium. Remember that we have assumed the number of interacting units to be large but finite, thereby generating small fluctuations under the condition 
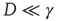. As a consequence, the temporal complexity illustrated in Figure 23.2 becomes ostensible only at criticality, while remaining virtually invisible in both the subcritical and supercritical regimes.
Figure 23.3 illustrates an important dynamical property of criticality concerning the fluctuations emerging as a finite-size effect. We have to stress that the fluctuations, bringing important information about the network's complexity, are defined by Eq. (23.16). We define the equilibrium autocorrelation function of the variate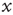 
, 
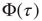, as
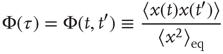
with the time difference
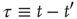
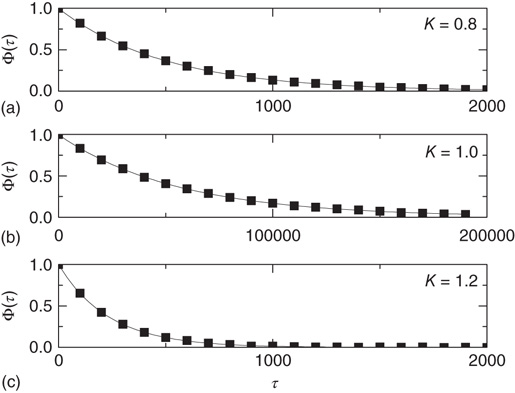
Figure 23.3 The equilibrium correlation function for the fluctuations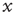 
in the subcritical (a), critical (b), and supercritical (c) cases, each considering 
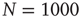units with 
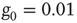. The scale of the exponential decay is increased by two orders of magnitude at criticality.
Figure 23.3 shows the important property that, at criticality, the equilibrium correlation function is markedly slower than in both the supercritical and the subcritical regimes. This property has to be kept in mind to appreciate the principal difference between ordinary and extended criticality. In fact, this is an indication that, with ordinary criticality, the significant effects of cooperation correspond to a single value of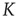 
, this being the critical value 
.
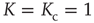23.2.2 Response to Perturbation
As far as the response to an external perturbation is concerned, it is important to address the issue of the connection with the phenomenon of complexity management [29]. We have noticed that, at criticality, the fluctuation in sign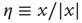 
is not ergodic for 
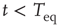, thereby implying that the transmission of information from one network to another may require a treatment going beyond the traditional Green–Kubo approach. To recover the important results of Ref. [29], we should adopt a dichotomous representation fitting the nature of the DMM units that have to choose between the two states 
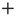and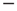 
. To simplify the numerical calculations, we assume that the influence of an external stimulus on the system is described by Eq. (23.21). This is a simplified picture that does not take into account that, in the case of flocks of birds [30], for instance, the single units make a decision based on the 
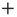or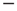 
sign of the stimulus rather than on its actual value. In other words, in the case of flocks [30], this would imply that the external stimulus assigns to each bird either the right or the left direction.
The perturbed time evolution of the mean field at criticality is described by
where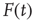 
is the external perturbation, and 
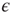a small dimensionless number that will serve the purpose of ensuring the linear response condition. The factor of 
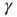is introduced for dimensional reasons.
We note that, in the diffusional transient regime, which is much more extended in time than that generated by the traditional Langevin equation, Eq. (23.21) becomes
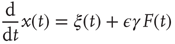
yielding the average response
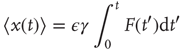
which, in the case where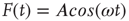 
, becomes
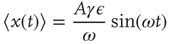
Taking into account that during the transient regime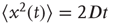 
, we immediately obtain
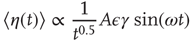
in accordance with the experimental observation [31] that the response of a non-ergodic system to harmonic perturbation generates damped oscillations.
The rigorous treatment would lead to
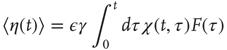
where
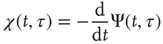
and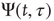 
is the aged survival probability [28].
As a consequence, we predict that, at criticality, the complex network obeys the principle of complexity management [29] when all the units are weakly perturbed by an external stimulus. The chapter of West et al. [5] in this volume shows that, because of cooperation, a strong perturbation on a limited number of units is the source of the related phenomenon of CI synchronization, which in this chapter we show to emerge also at the level of neural EC, under the form of neural network entrainment.
23.3 Neural Dynamics
The cooperation of units within the DMM at criticality generates the temporal complexity illustrated by Figure 23.2, which turns out to be a source of information transport. This transfer of information is especially convenient as shown in the recent work of Vanni et al. [30]. This cooperation property yields the surprising effect of the crucial role of committed minorities discussed in this volume by West et al. [5].
In this section, we illustrate a very similar property generated by a model of neurophysiological interest, with the surprising discovery that these effects do not rest on a single value of the cooperation strength, that is, on the magnitude of the control parameter. This suggests the conjecture that a new form of criticality, called extended criticality, may be invoked [10, 11].
We show that the DMM leads to Plenz's avalanches [21], which are now a well-established property of neural networks. The model proposed in this chapter interprets the avalanches as a manifestation of cooperation. We also show that the amount of cooperation-generating avalanches is responsible for the phenomenon of entrainment.
23.3.1 Mittag–Leffler Function Model Cooperation
First of all, let us examine how the Mittag–Leffler function models relaxation. Metzler and Klafter [32] explain how the Mittag–Leffler function established a compromise between two apparently conflicting complexity schools, the advocates of inverse power laws and the advocates of stretched exponential relaxation, see also West et al. [33]. We denote with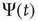 
the survival probability, that is, the probability that no event occurs up to time 
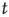, and we assign to its Laplace transform, 
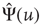, the following form (we adopt the notation for the Laplace transform 
):
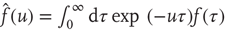with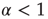 
. In the case 
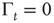, this is the Laplace transform of the Mittag–Leffler function [32], a generalization of the ordinary exponential relaxation which interpolates between the stretched exponential relaxation 
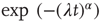, for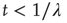 
and the inverse power law behavi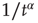or 
, for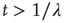 
.
Recent work [34] has revealed the existence of quakes within the human brain, and proved that the time interval between two consecutive quakes is well described by a survival probability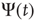 
, whose Laplace transform fits very well the prescription of Eq. (23.28). The parameter 
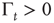has been introduced [34, 35] to take into account the truncation which is thought to be a natural consequence of the finite size of the time series under study. As a matter of fact, when 
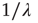is of the order of the time step and 
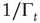is much larger than the unit time step, the survival probability turns out to be virtually an inverse power law, whereas when 
is of the order of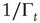 
and both are much larger than the unit time step, the survival probability turns out to be a stretched exponential function.
Failli et al. [35] illustrate the effect of establishing a cooperative interaction in the case of the random growth of surfaces. A growing surface is a set of growing columns whose height increases linearly in time with fluctuations, which, in the absence of cooperation, would be of Poisson type. The effect of cooperative interaction is to turn the Poisson fluctuations into complex fluctuations, the interval between two consecutive crossings of the mean value being described by an inverse power law waiting time distribution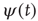 
, corresponding to a survival probability 
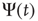, whose Laplace transform is given by Eq. (23.28). In conclusion, according to the earlier work [35], we interpret 
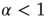as a manifestation of the cooperative nature of the process.
In this section, we illustrate a neural model where the time interval between two consecutive firings, in the absence of cooperation, is described by an ordinary exponential function, thereby corresponding to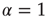 
. The effect of cooperation is to make 
decrease in a monotonic way, when increasing the cooperation strength,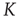 
, with no special critical value.
We note that Barabasi [36] stressed the emergence of the inverse power law behavior, properly truncated, as a consequence of the cooperative nature of human actions. Here we interpret the emergence of the Mittag–Leffler function structure as an effect of the cooperation between neurons. The emergence of a stretched exponential function confirms this interpretation if we adopt an intuitive explanation of it based on the distinction between the attempt to cooperate and to succeed. The action generator is assumed to not be fully successful, and a success rate parameter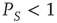 
is introduced with the limiting condition 
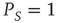corresponding to full success. To turn this perspective into a theory, yielding the theoretical prediction of Eq. (23.28), we assume that the time interval between two consecutive cooperative actions is described by the function 
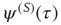, where the superscript (S) indicates that, from a formal point of view, we realize a process corresponding to subordination theory [37–41]. Here we make the assumption that the survival probability for an action, namely the probability that no action occurs up to a time 
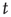after an earlier action, has the form
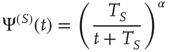
with
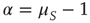
and
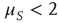
As a consequence, the time interval between two consecutive actions has the distribution density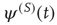 
of the form
Note that the distance between two actions is assumed to depart from the condition of ordinary ergodic statistical mechanics. In fact, the mean time distance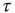 
between two consecutive actions emerging from the distribution density of Eq. (23.32) is
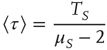
for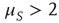 
and diverges for 
. As a consequence, this process shares the same non-ergodic properties as those generated by human action [36].
It is evident that, when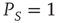 
, the survival probability 
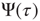is equal to 
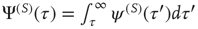. When, 
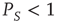, using the formalism of the subordination approach [34, 35, 37–39], we easily prove that the Laplace transform of 
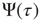is given by
where
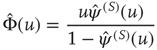
To prove the emergence of the Mittag–Leffler function of Eq. (23.28), with 
, from this approach, let us consider for simplicity the case where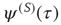 
is not truncated. In the non-ergodic case 
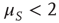, using the Laplace transform method [33], we obtain that the limiting condition 
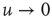yields Eq. (23.28) with
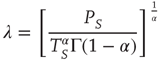
where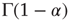 
is the Gamma function. Note that when 
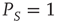, the Laplace transform of Eq. (23.34) in the limit of 
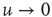coincides, as it must, with the Laplace transform of 
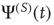. In conclusion, we obtain
with
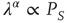
In the neural model illustrated here, we define a parameter of cooperation effort, denoted, as in the DMM case, by the symbol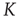 
. The success of cooperation effort is measured by the quantity
We determine that the sign of success is given by the number of neurons firing at the same time. We speculate that there is a connection with the dragon kings [42, 43] and coherence potentials [8].
23.3.2 Cooperation Effort in a Fire-and-Integrate Neural Model
The NFC model refers to the interaction between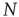 
neurons, each of which has a time evolution described by
where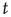 
is a natural number; 
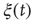is a variable getting either the value of 
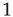or of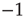 
, with equal probability, with no memory of the earlier values; and 
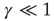so as to make the integer time virtually continuous when 
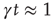. The quantity 
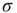is the noise intensity. The quantity 
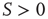serves the purpose of making the potential 
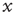essentially increase as a function of time. The neuron potential 
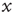moves from the initial condition 
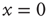and, through fluctuations around the deterministic time evolution corresponding to the exact solution of the case 
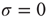[44], reaches the threshold value 
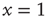. When the threshold is reached, it fires and resets back to the initial value 
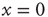. It is straightforward to prove that the variable 
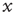can reach the threshold only when the condition
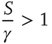
applies. In this case, the time necessary for the neuron to reach the threshold, called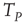 
, is given by
In the absence of interaction, the motion of each neuron is periodic, and the interval between two consecutive firings of the same neuron is given by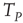 
. The real sequence of firings looks random, as a consequence of the assumption that the initial conditions of 
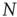neurons are selected randomly. In this case, the success rate 
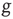is determined by the random distribution of initial conditions and can be very small, as we subsequently show.
The cooperative properties of the networks are determined as follows. Each neuron is the node of a network and interacts with all the other nodes linked to it. When a neuron fires, all the neurons linked to it make an abrupt step ahead of intensity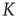 
. This is the cooperation parameter, or intensity strength. An inhibition link is introduced by assuming that, when one neuron fires, all the other neurons linked to it through inhibition links make an abrupt step backward.
This model is richly structured and may allow us to study a variety of interesting conditions. There is widespread conviction that the efficiency of a network, namely its capacity to establish global cooperative effects, depends on network topology, as suggested by the brain behavior [34, 45]. The link distribution itself, rather than being fixed in time, may change according to the Hebbian learning principle [16]. It is expected [16] that such learning generates a scale-free distribution, thereby shedding light on the interesting issue of burst leaders [46].
All these properties are studied elsewhere. In this chapter, we focus on cooperation by assuming that all the links are excitatory. To further emphasize the role of cooperation, we should make the ATA assumption adopted by Mirollo and Strogatz [44]. This assumption was also made in earlier work [47]. In spite of the fact that the efficiency of the ATA model is reduced by the action of the stochastic force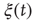 
which weakens the action of cooperation, thereby generating time complexity, the ATA condition generates the maximal efficiency and neuronal avalanches. However, this conditioninhibits the realization of an important aspect of cooperation, namely locality breakdown. For this reason, in addition to the ATA condition, we also study the case of a regular, two-dimensional (2D) network, where each node has four nearest neighbors and consequently four links. It is important to stress that, to make our model as realistic as possible, we should introduce a delay time between the firing of a neuron and the abrupt step ahead of all its nearest neighbors. This delay should be assumed to be proportional to the Euclidean distance between the two neurons, and it is expected to be a property of great importance to prove the breakdown of locality when the scale-free condition is adopted. The two simplified conditions studied in this chapter, ATA and 2D, would not be affected by a time delay, which should be the same for all the links. For this reason, we do not further consider time delay.
For the cooperation strength, we must assume the condition
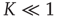
When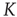 
is of the order of magnitude of the potential threshold 
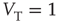, the collective nature of cooperation is lost because the firing of a few neurons causes an abrupt cascade in which all the other neurons fire. Thus, we do not consider to be important the non-monotonic behavior of network efficiency which our numerical calculations show to emerge by assigning 
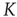values of the same order as the potential threshold.
We also note that, in the case of this model, the breakdown of the Mittag–Leffler structure, at large times, is not caused by a lack of cooperation but by the excess of cooperation. To shed light on this fact, keep in mind that this model has been solved exactly by Mirollo and Strogatz when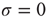 
[44]. In this case, even if we adopt initial random conditions, after a few steps, all the neurons fire at the same time, and the time distance between two consecutive firings is given by 
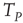of Eq. (23.42). As an effect of noise, the neurons can also fire at times 
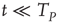, and consequently, setting 
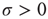, a new, and much shorter timescale is generated. When we refer to this as the timescale of interest, the Mirollo and Strogatz time 
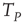plays the role of a truncation time and
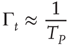
To examine this condition, let us assign to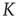 
a value very close to 
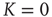. In this case, even if we assign to all the neurons the same initial condition, 
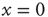, because of the presence of stochastic fluctuations, the neurons fire at different times, thereby creating a spreading on the initial condition that tends to increase in time, even if initially the firing occurs mainly at times 
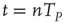. The network eventually reaches a stationary condition with a constant firing rate 
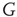given by
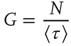
where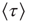 
denotes the mean time between two consecutive firings of the same neuron. For 
, 
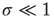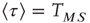. From the condition of a constant rate 
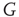, we immediately derive the Poisson waiting-time distribution
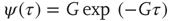
Consequently, this heuristic argument agrees very well with numerical results.
We consider a set of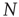 
identical neurons, each of which obeys Eq. (23.40), and we also assume, with Mirollo and Strogatz [44], that the neurons cooperate. For the numerical simulation, we select the condition
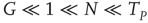
As a consequence of this choice, we obtain
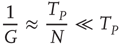
thereby realizing the earlier mentioned timescale separation. It is evident that this condition of the noninteracting neuron fits Eq. (23.28) with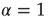 
and
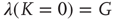
In this case, the time truncation is not perceived because of the condition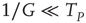 
.
In Figure 23.4, we show that the 2D condition is essentially equivalent to the ATA condition, provided that the cooperation strength is assumed to be an order of magnitude larger than that of the ATA condition. This is an important result, because in the case of a two-dimensional regular lattice, even though the neurons interact only with their nearest neighbors, the entire network generates the same sequence of bursts as in the ATA condition, provided that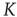 
is an order of magnitude larger. This is an indication of the fact that, when the critical values of 
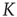are used, two neurons become closely correlated regardless of the Euclidean length of their link, which is a clear manifestation of locality breakdown.
Figure 23.4 The number of neurons firing per unit of time in the ATA (a) and 2D (b) conditions for 
ranging from no cooperation to a high level of cooperation. When increasing the value of 
, the system immediately departs from a Poisson process at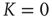 
to display complex cooperative behavior, which then becomes strongly periodic for large 
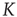. The 2D condition shares the behavior of the ATA condition, only requiring more cooperation.
As far as the Mittag–Leffler time complexity is concerned, we adopt the same fitting procedure as that used in Ref. [47]. We evaluate the Laplace transform of the experimental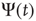 
, and use as a fitting formula Eq. (23.28) with 
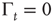, to find the parameter 
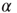. Then we fit the short-time region with the stretched exponential
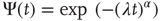
to find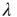 
. We determine that, in the 2D condition as in the ATA condition, switching on cooperation has the effect of generating the Mittag–Leffler time complexity. From Figure 23.5, we see that any nonvanishing value of 
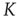turns the Poisson condition 
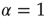into the Mittag–Leffler temporal complexity 
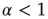. The only remarkable difference is that, in the case of large cooperation strength, the value of 
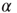tends to the limiting value of 
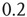, whereas the ATA condition brings it to the limiting value of 
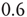. Statistical analysis of data from real experiments may use this property to assess the topology of the neural network. It is expected, in fact, that all network topologies generate the Mittag–Leffler time complexity, but the actual value of 
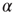depends on the network topology. Thus, the joint use of theory and experiment may further our understanding of the neural network structure.
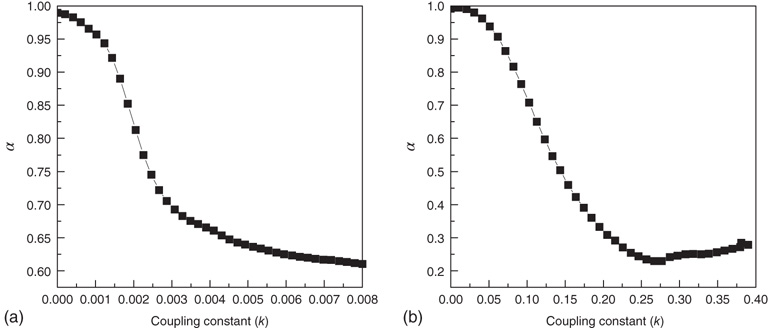
Figure 23.5 The value of the Mittag–Leffler parameter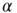 
for different cooperation levels in the ATA (a) and 2D (b) conditions. For any nonzero 
, 
, signifying Mittag–Leffler temporal complexity.
It is interesting to notice that Figure 23.6, in accordance with our expectation [see Eq. (23.39), shows that the success rate undergoes a significant increase at the value of the cooperation parameter 
at which a distinctly Mittag–Leffler survival probability emerges.
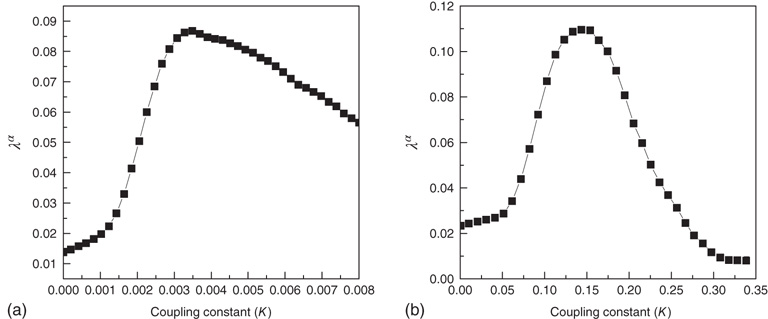
Figure 23.6 The value of the Mittag–Leffler parameter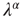 
for different cooperation levels in the ATA (a) and 2D (b) conditions. In both cases, the success rate significantly increases at the values of the cooperation strength, making 
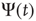depart from the condition of stretched exponential relaxation.
23.4 Avalanches and Entrainment
Neurophysiology is a field of research making significant contributions to the progress of the science of complexity. Sornette and Ouillon [42], who are proposing the new concept of dragon kings to go beyond the power law statistics shared by physical, natural, economic, and social sciences, consider the neural avalanches found by Plenz [21] to be a form of extreme events that are not confined to neurophysiology and may show up also at the geophysical and economic level. The increasing interest in neural avalanches is connected to an effort to find a proper theoretical foundation, for which self-organized criticality [3] is a popular candidate, in spite of a lack of a self-contained theoretical derivation.
On the other hand, neurophysiology is challenging theoreticians with the well-known phenomenon of neural entrainment. At first sight, the phenomenon of neural entrainment, which is interpreted as the synchronization of the dynamics of a set of neurons with an external periodic signal, may be thought to find an exhaustive theoretical foundation in the field of chaos synchronization [48]. This latter phenomenon has attracted the attention of many scientists in the last 22 years since the pioneering paper by Pecora and Carroll [49]. However, this form of synchronization seems to be far beyond the popular chaos synchronization. According to the authors of Ref. [50], the auditory cortex neurons, under the influence of a periodic external signal, are entrained with the stimulus in such a way as to be in the excitatory phase when the stimulus arrives, in order to process it in the most efficient way [50]. The work of neurophysiologists [51] is, on one hand, a challenge for physicists because the experimental observation should force them to go beyond the conventional theoretical perspective of coupled oscillators, combining regular oscillations with irregular network activity while establishing a close connection with the ambitious issue of cognition [52]. Setting aside the latter, we can limit ourselves to noticing with Gross and Kowalski [6] that the entrainment between different channels of the same networks is due to excitatory synapses and consequently to neuron cooperation, rather than to the behavior of single neurons that never respond in the same way to the same stimulus.
Neural entrainment, on the contrary, is a global property of the whole network which is expected to generate the same response to the same stimulus. In this sense, it has a close similarity with the phenomenon of chaos synchronization, insofar as entrainment is a property of a single realization. The phenomenon of complexity management [29], on the other hand, requires averages over many responses to the same stimulus to make evident the correlation that an experimentalist may realize between response and stimulus, after designing the stimulus, so as to match the complexity of the system.
Our theoretical model generates both avalanches and entrainment, thereby making clear that the phenomenon of neural entrainment is quite different from that of chaos synchronization, in spite of the fact that it shares with the latter the attractive property of being evident at the level of single realizations. Figure 23.7 depicts an avalanche, with the typical power index of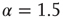 
, generated by the theoretical model of this chapter, in the case of a two-dimensional regular lattice, with 
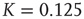, a strong cooperation value, corresponding to the realization of a sequence of well defined bursts, as illustrated in Figure 23.4.
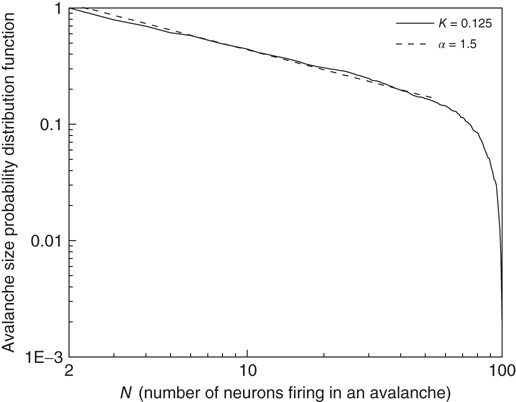
Figure 23.7 The avalanche size distribution in the 2D condition with cooperation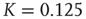 
. The slope of the distribution is given by the power index 
.
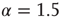As a phenomenon of entrainment we have in mind that of the pioneering work of Ref. [23]. These authors generated a condition of maximal cooperation by chemically killing the inhibitory links, and using as a stimulus a periodic electrical stimulation. The entrainment of two 2D neural network models is shown in Figure 23.8. Here we replace the periodic external stimulation with a neural network 
identical to the perturbed neural network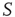 
. In addition, we assume that only 
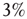of the nodes of 
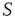are forced to fire at the same time as the neurons of the network 
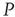. This is a condition similar to that adopted elsewhere [30], with the 
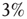of nodes of 
playing the same roles as the lookout birds [30]. These “look out” neurons are also similar to the committed minorities [5] used to realize the phenomenon of CI synchronization.
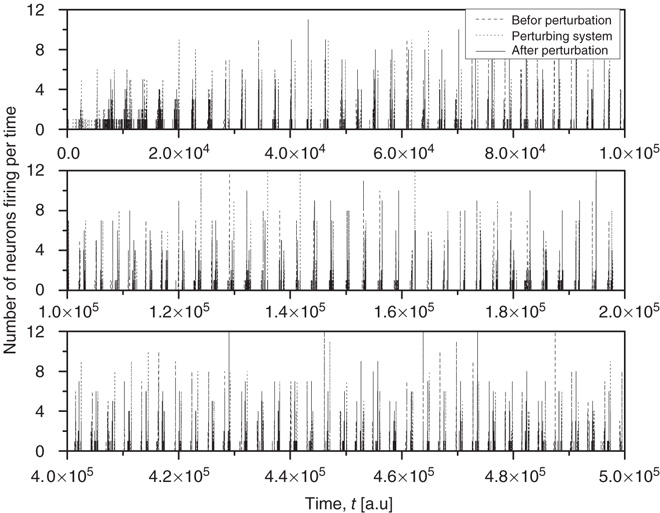
Figure 23.8 The entrainment of the 2D neural network 
(dashed lines) to an identical neural network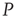 
(dotted lines) through the forced perturbation of 
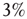of the nodes of 
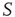. The avalanches of the perturbed network 
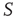(solid lines) become synchronized to the perturbing network 
.
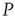23.5 Concluding Remarks
There is a close connection between avalanches and neural entrainment. Criticality plays an important role to establish this connection, because, as is well known in the field of phase transition, at criticality, as an effect of long-range correlation, the limiting condition of local interaction is lost, and an efficient interaction between units that would not be correlated in the absence of cooperative interaction is established. This condition is confined to criticality, thereby implying that “intelligent” systems operate at criticality. Quite surprisingly, the model of neural dynamics illustrated in this chapter generates long-range interactions, so as to realize entrainment, for a wide range of values of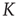 
. This seems to be the EC advocated by Longo and coworkers [10, 11].
What is the relation between these properties and the emergence of consciousnesswhich, according to Werner [13], must be founded on RGT? A theory as rigorous as RGT should be extended to the form of criticality advocated by Longo and coworkers [10, 11], and this may be a difficult issue making it more challenging, but not impossible, to realize the attractive goal of Werner [13]. Werner found it very promising to move along the lines outlined by Allegrini and coworkers [25] with their discovery that an intermittent behavior similar to that of Figure 23.2, with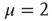 
, may reflect cognition.
A promising but quite preliminary result is that of Ref. [24]. Making the assumption that cognition enters into play, with the capability of making choices generated by the intelligent observation of the decision made by the whole system, and moving along the lines that led us to Eq. (23.17), the authors of Ref. [24] found the following equation:
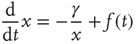
which generates an intermittent process with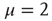 
, as illustrated in Ref. [24]. We think that this results suggests two possible roads, both worthy of investigation.
The first way to realize this ambitious purpose is based on a model similar to the DMM. The units cooperate through a structure similar to that of Eqs. (23.1)–(23.4). A given unit may make its decision on the basis of the history of the units linked to it rather than on their state at the time at which it makes its decision. This may be a dramatic change, with the effect of generating complexity for an extended range of the control parameter.
The second way is based on a model similar to the NFC model, namely the cooperative neuron model, where each unit, in the absence of cooperation, is driven by Eq. (23.40). In this model, each unit has a time evolution that depends on the earlier history of the units linked to it, thereby fitting the key condition of earlier work [24]. To proceed along these lines we should settle a still open problem. The condition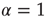 
, where the Mittag–Leffler function obtained from the inverse Laplace transform of Eq. (23.37) becomes an ordinary exponential function, is a singularity where the waiting-time distribution density 
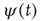, with index 
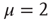, may be abruptly replaced by a fast decaying function, an inverse power law with index 
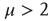, and, in principle, also by an exponential function. From an intuitive point of view, this weird condition may be realized by curves of the type of those of Figure 23.5, with the parameter 
(
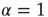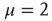) remaining unchanged for an extended range of 
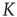values. In other words, 
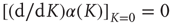. It is important to notice that the statistical analysis made by the authors of Ref. [53] to associate cognition with 
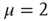is based on observing the rapid transition processes (RTPs) occurring in electroencephalography (EEG) monitoring different brain areas. These authors define the simultaneous occurrence of two or more RTPs as crucial events and determined that the waiting-time distribution density 
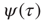, where 
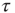is the time interval between two consecutive crucial events, is characterized by 
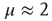. This suggests that the authors of Ref. [53] had in mind a cooperation model similar to the NFC model of this chapter, thereby making plausible our conjectures that a connection can be established between the DMM and NFC models of this chapter and the cognition model [24].
In spite of conceptual and technical difficulties that must be surpassed to achieve the important goal of Werner [13], we share his optimistic view [15]: “On account of this, self-similarity in neural organizations and dynamics poses one of the most intriguing and puzzling phenomenon, with potentially immense significance for efficient management of neural events on multiple spatial and temporal scales.”
References
- 1. Beggs, J.M. and Plenz, D. (2003) Neuronal avalanches in neocortical circuits. J. Neurosci., 23 (35), 11–167.
- 2. Touboul, J. and Destexhe, A. (2010) Can power-law scaling and neuronal avalanches arise from stochastic dynamics? PLoS One, 5 (2), e8982.
- 3. de Arcangelis, L. and Herrmann, H. (2012) Activity-dependent neuronal model on complex networks. Front. Physiol., 3, 62.
- 4. Li, X. and Small, M. (2012) Neuronal avalanches of a self-organized neural network with active-neuron-dominant structure, arXiv preprint arXiv:1204.6539.
- 5. West, B., Turalska, M., and Grigolini, P. (2013) Complex Networks: From Social Crises to Neuronal Avalanches, in this Volume, John Wiley & Sons.
- 6. Gross, G. and Kowalski, J. (1999) Origins of activity patterns in self-organizing neuronal networks in vitro. J. Intell. Mater. Syst. Struct., 10 (7), 558–564.
- 7. Chialvo, D. (2010) Emergent complex neural dynamics. Nat. Phys., 6 (10), 744–750.
- 8. Plenz, D. (2012) Neuronal avalanches and coherence potentials. Eur. Phys. J.-Spec. Top., 205 (1), 259–301.
- 9. Stanley, H. (1971) Introduction to phase transitions and critical phenomena, Introduction to Phase Transitions and Critical Phenomena, Clarendon Press.
- 10. Bailly, F. and Longo, G. (2011) Mathematics and the Natural Sciences: The Physical Singularity of Life, Imperial College Press, Singapore.
- 11. Longo, G. and Montévil, M. (2012) The inert vs. the living state of matter: extended criticality, time geometry, anti-entropy–an overview. Front. Physiol., 3, 39.
- 12. Montroll, E. (1981) On the dynamics of the ising model of cooperative phenomena. Proc. Natl. Acad. Sci. U.S.A., 78 (1), 36–40.
- 13. Werner, G. (2013) Consciousness viewed in the framework of brain phase space dynamics, criticality, and the renormalization group. Chaos, Solitons & Fractals, 55, 3–12.
- 14. Werner, G. (2007) Metastability, criticality and phase transitions in brain and its models. Biosystems, 90 (2), 496–508.
- 15. Werner, G. (2011) Letting the brain speak for itself. Front. Physiol., 2, 60.
- 16. Turalska, M., Geneston, E., West, B., Allegrini, P., and Grigolini, P. (2012) Cooperation-induced topological complexity: a promising road to fault tolerance and hebbian learning. Front. Physiol., 3, 52.
- 17. Fraiman, D., Balenzuela, P., Foss, J., and Chialvo, D. (2009) Ising-like dynamics in large-scale functional brain networks. Phys. Rev. E, 79 (6), 061–922.
- 18. Green, M. (1954) Markoff random processes and the statistical mechanics of time-dependent phenomena. II. Irreversible processes in fluids. J. Chem. Phys., 22, 398.
- 19. Kubo, R. (1957) Statistical-mechanical theory of irreversible processes. i. general theory and simple applications to magnetic and conduction problems. J. Phys. Soc. Jpn., 12 (6), 570–586.
- 20. Turalska, M., Lukovic, M., West, B., and Grigolini, P. (2009) Complexity and synchronization. Phys. Rev. E, 80 (2), 021–110.
- 21. Klaus, A., Yu, S., and Plenz, D. (2011) Statistical analyses support power law distributions found in neuronal avalanches. PloS One, 6 (5), e19–779.
- 22. Gerstner, W. and Kistler, W. (2002) Spiking Neuron Models: Single Neurons, Populations, Plasticity, Cambridge university press.
- 23. Gross, G., Kowalski, J., and Rhoades, B. (1999) Spontaneous and evoked oscillations in cultured mammalian neuronal networks, in Oscillations in Neural Systems, Vol. 1, (eds D. Levine, V. Brown, and T. Shirey), Erlbaum Associates, New York, pp. 3-29.
- 24. Palatella, L. and Grigolini, P. (2012) Noise-induced intermittency of a reflexive model with symmetry-induced equilibrium. Physica A, 391 (23) 5900–5907.
- 25. Allegrini, P., Menicucci, D., Bedini, R., Gemignani, A., and Paradisi, P. (2010) Complex intermittency blurred by noise: theory and application to neural dynamics. Phys. Rev. E, 82 (1), 015–103.
- 26. Bianco, S., Geneston, E., Grigolini, P., and Ignaccolo, M. (2008) Renewal aging as emerging property of phase synchronization. Physica A, 387 (5), 1387–1392.
- 27. Bianco, S., Grigolini, P., and Paradisi, P. (2005) Fluorescence intermittency in blinking quantum dots: Renewal or slow modulation?, J. Chem. Phys., 123 (17), 174704 (1–10).
- 28. Svenkeson, A., Bologna, M., and Grigolini, P. (2012) Linear response at criticality. Phys. Rev. E, 86 041145(1–10).
- 29. Aquino, G., Bologna, M., Grigolini, P., and West, B. (2010) Beyond the death of linear response: 1/f optimal information transport. Phys. Rev. Lett., 105 (4), 40–601.
- 30. Vanni, F., Lukovi
, M., and Grigolini, P. (2011) Criticality and transmission of information in a swarm of cooperative units. Phys. Rev. Lett., 107 (7), 78–103. - 31. Allegrini, P., Bologna, M., Fronzoni, L., Grigolini, P., and Silvestri, L. (2009a) Experimental quenching of harmonic stimuli: universality of linear response theory. Phys. Rev. Lett., 103 (3), 30–602.
- 32. Metzler, R. and Klafter, J. (2002) From stretched exponential to inverse power-law: fractional dynamics, Cole–Cole relaxation processes, and beyond. J. Non-Cryst. Solids, 305 (1), 81–87.
- 33. West, B., Bologna, M., and Grigolini, P. (2003) Physics of Fractal Operators, Springer.
- 34. Bianco, S., Ignaccolo, M., Rider, M., Ross, M., Winsor, P., and Grigolini, P. (2007) Brain, music, and non-poisson renewal processes. Phys. Rev. E, 75 (6), 061–911.
- 35. Failla, R., Grigolini, P., Ignaccolo, M., and Schwettmann, A. (2004) Random growth of interfaces as a subordinated process. Phys. Rev. E, 70 (1), 010–101.
- 36. Barabasi, A. (2005) The origin of bursts and heavy tails in human dynamics. Nature, 435 (7039), 207–211.
- 37. Sokolov, I. (2000) Lévy flights from a continuous-time process. Phys. Rev. E, 63 (1), 011–104.
- 38. Barkai, E. and Silbey, R. (2000) Distribution of variances of single molecules in a disordered lattice. J. Phys. Chem. B, 104 (2), 342–353.
- 39. Metzler, R. and Klafter, J. (2000) From a generalized Chapman-Kolmogorov equation to the fractional Klein-Kramers equation. J. Phys. Chem. B, 104 (16), 3851–3857.
- 40. Gorenflo, R., Mainardi, F., and Vivoli, A. (2007) Continuous-time random walk and parametric subordination in fractional diffusion. Chaos, Solitons & Fractals, 34 (1), 87–103.
- 41. Sokolov, I. and Klafter, J. (2005) From diffusion to anomalous diffusion: a century after einstein's brownian motion. Chaos, 15, 026103–026109.
- 42. Sornette, D. and Ouillon, G. (2012) Dragon-kings: mechanisms, statistical methods and empirical evidence. Eur. Phys. J.-Spec. Top., 205 (1), 1–26.
- 43. Werner, T., Gubiec, T., Kutner, R., and Sornette, D. (2012) Modeling of super-extreme events: an application to the hierarchical weierstrass-mandelbrot continuous-time random walk. Eur. Phys. J.-Spec. Top., 205 (1), 27–52.
- 44. Mirollo, R. and Strogatz, S. (1990) Synchronization of pulse-coupled biological oscillators. SIAM J. Appl. Math., 50 (6), 1645–1662.
- 45. Kim, B. (2004) Geographical coarse graining of complex networks. Phys. Rev. Lett., 93 (16), 168–701.
- 46. Ham, M., Bettencourt, L., McDaniel, F., and Gross, G. (2008) Spontaneous coordinated activity in cultured networks: analysis of multiple ignition sites, primary circuits, and burst phase delay distributions. J. Comput. Neurosci., 24 (3), 346–357.
- 47. Lovecchio, E., Allegrini, P., Geneston, E., West, B., and Grigolini, P. (2012) From self-organized to extended criticality. Front. Physiol., 3, 98.
- 48. Pikovsky, A., Rosenblum, M., and Kurths, J. (2003) Synchronization: A Universal Concept in Nonlinear Sciences, Vol. 12, Cambridge University Press.
- 49. Pecora, L. and Carroll, T. (1990) Synchronization in chaotic systems. Phys. Rev. Lett., 64 (8), 821–824.
- 50. Schroeder, C. and Lakatos, P. (2009) Low-frequency neuronal oscillations as instruments of sensory selection. Trends Neurosci., 32 (1), 9–18.
- 51. Wang, X. (2010) Neurophysiological and computational principles of cortical rhythms in cognition. Physiol. Rev., 90 (3), 1195–1268.
- 52. Dehaene, S. and Changeux, J. (2011) Experimental and theoretical approaches to conscious processing. Neuron, 70 (2), 200–227.
- 53. Allegrini, P., Menicucci, D., Bedini, R., Fronzoni, L., Gemignani, A., Grigolini, P., West, B., and Paradisi, P. (2009b) Spontaneous brain activity as a source of ideal 1/f noise. Phys. Rev. E, 80 (6), 061–914.