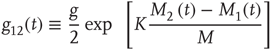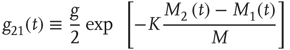24
Complex Networks: From Social Crises to Neuronal Avalanches

Bruce J. West, Malgorzata Turalska and Paolo Grigolini

24.1 Introduction

Complex networks ranging from social gatherings to neuron clusters are described by highly heterogeneous, scale-free degree distributions [1, 2]. The seminal paper of Watts and Strogatz [3] established that real-world networks are distinct from the totally random theoretical networks of Erdös and Renyi [4]. The latter investigators established that networks with completely random connections have unimodal distributions of connections between elements. Real-world networks, on the other hand, are found not to be characterized by such weak clustering and, instead, show surprisingly large clustering coefficients. Several mechanisms have been proposed to explain the observed topology [1, 2, 5–8], the most popular one being that of preferential attachment, which is based on the assumption that scale-free networks grow in time and that the newly arriving elements tend to establish connections preferentially with the elements having the larger number of links [1, 5]. However, there exists a wide class of networks that do not originate by preferential attachment or growth, and the model presented here catalogs the properties of these latter networks.

Two central concepts arising in the application of dynamic networks to the understanding of the measurable properties of the brain have to do with topology and criticality. Topology is related to the inverse power-law distributions of such newly observed phenomena as neuronal avalanches [9], and criticality [2] has to do with the underlying dynamics that gives rise to the observed topology. Criticality was first systematically observed in physics for systems undergoing phase transitions as a control parameter is varied: for example, as temperature is lowered, water transitions from the liquid to the solid phase. Many physical systems consisting of a large number of structurally similar interacting units have properties determined by local interactions. At the critical value of the control parameter, the interactions suddenly change from local to long-range, and what had been the superposition of independent dynamic elements becomes dominated by long-range interactions and coordinated activity. The dynamical source of these properties is made explicit through the development of the decision-making model (DMM), which is shown to be related to but distinctly different from the Ising model used by others in explaining criticality in the context of the brain.

Here, we present a way to generate topology characterized by the scale-free degree distribution 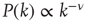, where 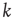is the number of links to an element, using the underlying network dynamics. We confirm that the scale-free topology emerges from the dynamical interactions between the elements of the network [2, 8]. Moreover, we show that, for a critical value of the control parameter 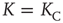, the cooperative interaction between the dynamical elements of a regular two-dimensional lattice generates a phase transition in which the majority of the elements transition to a critical state. This critical state has a scale-free network of interdependent elements with .

The perspective of assessing a network's complexity solely by means of its topology has been widely adopted. Here, we adopt a different point of view and emphasize the emergence of temporal complexity through the intermittency of events in time, as well as through topological complexity entailed by the dynamics. An event is interpreted as a transition of a global variable from one critical state to another. In this way, we identify two distinct forms of complexity: one associated with the connectivity of the elements of the network, and the other associated with the variability of the time interval between events. Both power laws are a consequence of criticality.

This manifestation of dual complexity is demonstrated using a simple DMM [10–12] introduced in Section 24.2. We show by direct calculation that a DMM network undergoes a phase transition similar to that observed in the Ising model [2] resulting in an inverse power-law distribution in the connectivity of the network elements. In Section 24.3, we distinguish between a static network, where the constitutive elements form an unchanging structure, and a dynamic network generated by the self-organization of the elements located on the backbone structure of the former. We explore the propensity for cooperation of both the static and dynamic networks. These dynamic-based results are interpreted in a neuroscience context. In Section 24.4, temporal complexity is discussed, and calculations reveal a scale-free distribution density of the consensus times , , which is separate and distinct from the scale-free degree distribution. The consensus time is the length of time the majority of the elements stay within one of the two available states. A handful of inflexible elements can have a dramatic influence on the overall behavior of the network, as we demonstrate in Section 24.5. Some conclusions are drawn in Section 24.6.

24.2 The Decision-Making Model (DMM)

The network dynamics of each element of a DMM network are determined by the two-state master equation [11, 12]

24.1

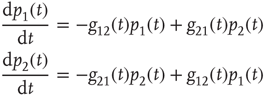
where 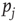is the probability of being in the state . The DMM uses a social paradigm of decision makers who choose between the state 1 (yes or ) and the state 2 (no or 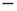) at each point in time 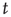. The interaction among the elements in the network is realized by setting the coupling coefficients to the time-dependent forms:

24.2

24.3

Here, M denotes the total number of nearest neighbors to each element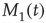, and and 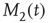give the numbers of nearest neighbors in the decision states “yes” and “no,” respectively.

The single individuals are not static but change their opinions over time, thereby making 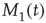and 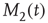fluctuate in time, while, of course, the total number of nearest neighbors is conserved, that is, 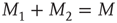. A single element in isolation has a vanishing control parameter 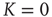and consequently would fluctuate between “yes” and “no,” with Poisson statistics at the rate .

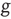When 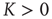, an element in the state “yes” (“no”) makes a transition to the state “no” (“yes”) faster or slower according to whethe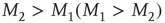r or 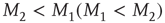, respectively. The quantity 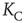is the critical value of the control parameter 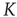, at which point a phase transition to a self-organized global majority state occurs. The efficiency of a network in facilitating consensus can be expressed as a quantity proportional to 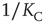. Here, that self-organized state is identified as the consensus. On the other hand, expressing network efficiency through consensus has the effect of establishing a close connection between network topology and the ubiquitous natural phenomenon of synchronization. In this way, a number of investigators have concluded that topology plays an important role in biology, ecology, climatology, and sociology [13–16].

We define the global variable in order to characterize the network fluctuations, as

24.4

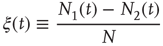
where 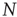is the total number of elements, and and 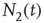are the number of elements in the state “yes” and “no” at time 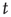, respectively. Typical DMM calculations of the global variable for the control parameter greater than the critical value in the all-to-all coupling configuration are shown on Figure 24.1 for three sizes of the network. The variability in the time series resembles thermal fluctuations in physical processes, but there is no such mechanism in the DMM. The erratic fluctuations are the result of the finite number of elements in the network.

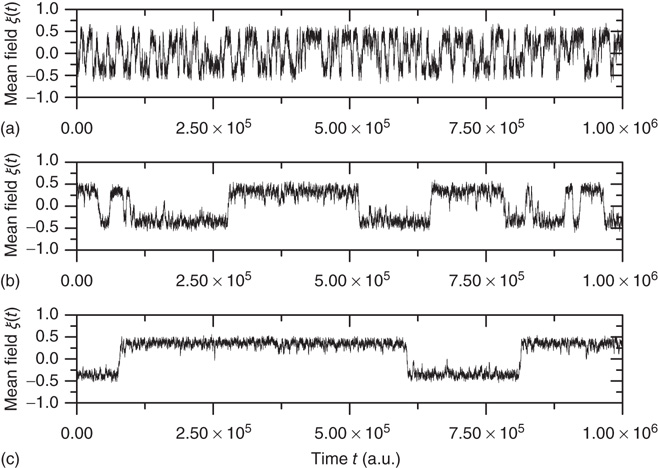
Figure 24.1 The fluctuation of the mean-field global variable as a function of time. For the network configuration: (a) 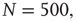(b) 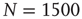, and (c) 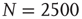. In all cases, 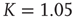and 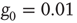. Adopted from Ref. [11].

The top panel in Figure 24.1 has the results for the fewest number of elements, in which case the dynamics seem to yield noise. In the middle panel, the number of elements is tripled from that in the top panel and the two states of the DMM are now evident, but the fluctuations persist. In the bottom panel, the number of elements is increased by a factor of five from the top panel and the critical states are even sharper. It is clear that the fluctuations vanish as the number of elements increase to infinity and they do so as 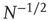. In a similar way, the size of the fluctuations decreases with increasing control parameter values.

We evaluate the time duration 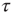of the consensus state, where eithe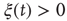r or 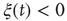, and calculate the time average of the modulus 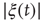. We denote this average with the symbol 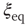in the sequel.

Note that in the special case, when the number of nearest neighbors 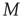is the same for all the nodes and the natural transition rate is very small 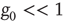, the DMM generates a phase transition that is analogous to the two-dimensional Ising model discussed in the seminal paper of Onsager [17]. This is an expected result insofar as the Ising model rests on the Hamiltonian

24.5

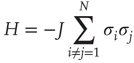
where 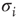and 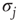denote the Pauli operators with eigenvalues 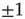. Equilibrium is defined in terms of Boltzmann distribution described by the density matrix

24.6

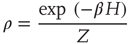
with the inverse of the temperature given by 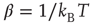, with 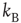being Boltzmann's constant and 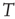the absolute temperature. Thus, the off-diagonal elements of the transfer matrix [18] become equivalent to the transition rates of Eqs. (24.2) and (24.3), under the condition that the control parameter is associated with the physical temperature, 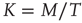. As examples of conditions yielding this equivalence, we consider two cases. The first case is for all-to-all coupling, where 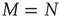and there is no spatial structure for the network. The second case is a simple two-dimensional lattice where each node is coupled to its four nearest neighbors, thereby yielding .

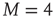The thermodynamic condition 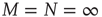was discussed extensively by authors of Ref. [10, 11], who showed that under those conditions the ratios 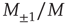are equivalent to the probabilities 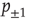for a node 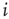to be in one of two allowed states. The dynamic evolution of a single unit state is then described by a two-state master equation

24.7

24.8

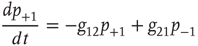
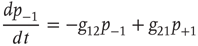
Solving this master equation using the difference in probabilities as a new variable 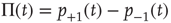, which corresponds to the earlier defined global order parameter 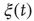, we obtain the mean-field equation

24.9

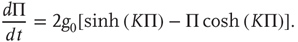
This equation yields two solutions, corresponding to global majority states, for the values of coupling constant 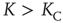, where the critical value of the control parameter .

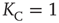The solution in the second case, where 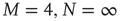, can be found in [19] and yields the critical value of the coupling constant 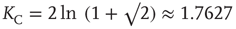, which value corresponds to the critical temperature in the Ising model [17].

In Figure 24.2, the DMM is seen to undergo phase transitions at the two critical values mentioned. We see that, for a very small value of the coupling strength 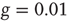, the numerical evaluation of 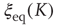on a 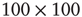lattice is very close to the theoretical prediction of Onsager [17]. The patterns generated by the Ising model at criticality corresponds to the emergence of correlation links yielding a scale-free network statistically indistinguishable from that observed experimentally within the brain using functional magnetic resonanceimaging.

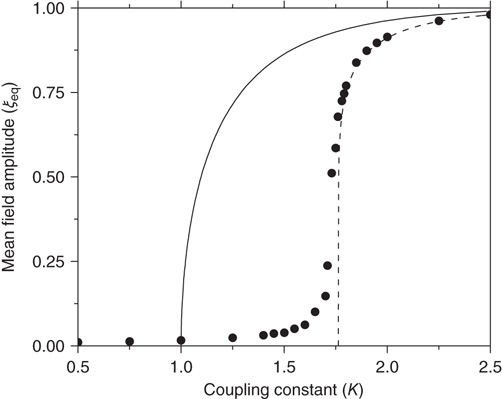
Figure 24.2 The phase diagram for the global variable 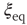. The solid and dashed lines are the theoretical predictions for the fully connected and two-dimensional regular lattice network, respectively. In both cases, 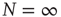and the latter case is the Onsager prediction [17]. The circles are the DMM calculation for 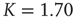. (Adopted from Ref. [12].)

This equivalence between the DMM and the Ising model is a formal one, because the DMM does not have a physical origin (no Hamiltonian) and it does not require the action of a thermal bath at temperature 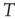to generate fluctuations as does the Boltzmann picture. This explains why the equivalence with the Ising model requires that 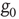vanish, so as to freeze the dynamics of the single units, in the absence of cooperation.

24.3 Topological Complexity

To realize temporal as well as topological complexity, we rely on numerical results and focus our attention on the condition 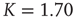, which, although slightly smaller than the Onsager theoretical prediction, is compatible with the emergence of cooperative behavior due to the phase transition. To derive the dynamically induced network topology, we apply the so-called correlation network approach, where a topology is generated by linking only those elements with cross-correlation levels above a given threshold [2]. Thus, we evaluate the two-point cross-correlation coefficient between all pairs of elements after the transients have faded in the DMM calculation. If the cross-correlation coefficient between two network elements is larger than the arbitrarily chosen threshold value 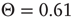, we insert a link between them; if not, we leave them uncoupled. This prescription is found to generate a scale-free network with the inverse power index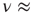 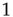, as shown in Figure 24.3. We also evaluate the distribution density 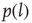of the Euclidian distance 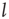between two linked elements and find that the average distance is of the order of 50, which is on the order of the size of the two-dimensional grid 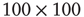. This average distance implies the emergence of long-range links that go far beyond the nearest neighbor coupling and is essential to realizing the rapid transfer of information over a complex network [21–23].

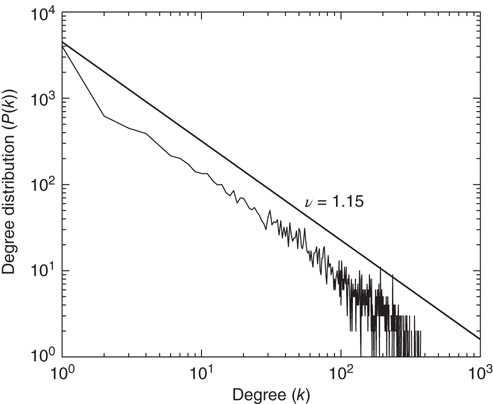
Figure 24.3 The degree distribution for the dynamically generated complex topology created by examining the dynamics of elements placed on a two-dimensional regular lattice with the parameter values 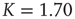and 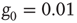in the DMM. (Adapted from Ref. [20].)

We construct from the DMM dynamically induced network a network backbone, called a dynamically generated complex topology (DGCT) and then study its efficiency by implementing the DMM dynamics on it. It is convenient to compare the cooperative behavior of the DGCT network with another seemingly equivalent scale-free degree network with the same 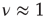. This latter scale-free network uses a probabilistic algorithm [24] and we refer to it as an ad hoc network, and implement the DMM on it as well as on the DGCT network. The phase-transition diagrams of the DGCT and the ad hoc network are illustrated in Figure 24.4a and the inset of Figure 24.4b, respectively. Notice that the phase transition occurs on both networks at 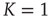, that is, at the same critical value corresponding to the all-to-all coupling condition. However, in Figure 24.4a a new phenomenon is observed, that being the emergence of both a consensus and a non-consensus state. The new state emerges because the self-organization process generates two weakly coupled identical clusters, each cluster being equivalent to an ad hoc network with 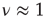. These two networks are virtually independent of each other, thereby yielding the states 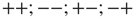, with equal probability. 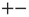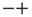The states and are the non-consensus states. To support this interpretation, we generate two identical ad hoc networks with 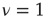and couple them with a single link. The resulting phase diagram, shown in Figure 24.4b, is very similar to that depicted in Figure 24.4a, thereby establishing that DGCT networks may give rise to the coexistence of communities with conflicting opinions, reminiscent of recent results obtained by others [25]. This result could not be obtained in the weak coupling limit where DMM becomes equivalent to the Ising model.

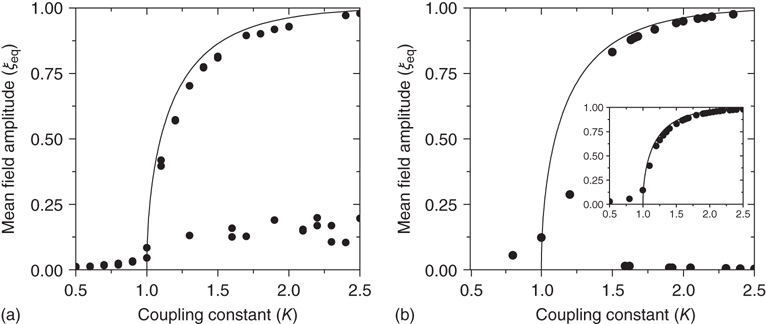
Figure 24.4 The phase diagram for global variable 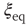. (a) The solid line corresponds to the equilibrium states obtained in the case of fully connected 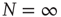network. Dots correspond to the equilibrium states obtained by evaluating the dynamics of the DMM on the DGCT network with 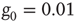. (b) The solid line corresponds to the equilibrium states obtained in the fully connected case for the 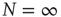network. Dots correspond to the equilibrium states obtained by evaluating the dynamics of the DMM on a system of two scale-free, ad hoc networks with power-law index 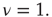Both networks had 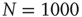elements and were coupled with only one link and 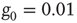. The inset shows the phase diagram for an ad hoc network with 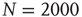elements and power-law index of the degree distribution 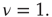(Adapted from Ref. [20].)

The earlier illustrated approach is consistent with the procedure widely adopted in neuroscience to define functional connections between different brain regions [2, 26]. Numerous studies have shown the scale-free character of networks created by correlated brain activity as measured through EEG [27, 28], magnetoencephalography [26], or magnetic resonance imagining [29]. Fraiman et al. [2] used the Ising model to explain the origin of the scale-free neuronal network and found the remarkable result that the brain dynamics operate at the corresponding critical state. The present research was, in part, inspired by these results [2], and leads to the additional discovery that the emergence of consensus produces long-range connections as well as a scale-free topology.

Consider the earlier results in the light of the recent experimental findings on brain dynamics [30]. The analysis of Bonifazi et al. [30] established that, in a manner similar to other biological networks, neural networks evolve by gradual change, incrementally increasing their complexity, and rather than growing along the lines of preferential attachment, neurons tend to evolve in a parallel and collective manner. The function of the neuronal network is eventually determined by the coordinated activity of many elements, with each element contributing only to local short-range interactions. However, despite this restriction, correlation is observed between sites that are not adjacent to each other, which is a surprising property suggesting the existence of a previously incomprehensible long-distance communication [31, 32]. The DMM dynamical approach affords the explanation that the local but cooperative interactions embed the elements in a phase-transition condition that is compatible with long-range interdependence.

24.4 Temporal Complexity

Let us now turn our attention to temporal complexity. We show that the apparently intuitive notion that topological complexity with a scale-free distribution of links 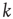, 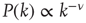and time complexity with a scale-free distribution of consensus times 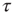, 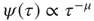are closely related is wrong. Figure 24.5 illustrates the consensus survival probability 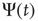corresponding to the critical value of the control parameter 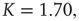generating the scale-free topology of Figure 24.3. Although emerging from a simple spatial network, that is, one with no structural complexity, the survival probability is scale-free with 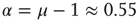over more than four time decades.

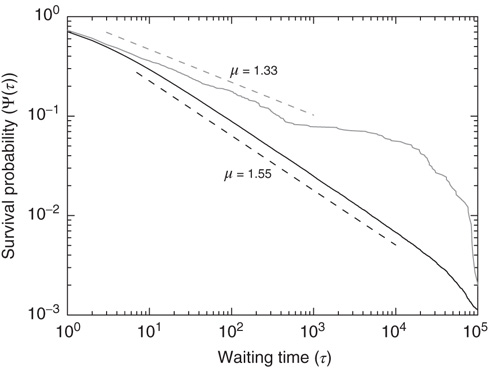
Figure 24.5 Consensus survival probability. Black and gray solid lines refer to the DMM implemented on a two-dimensional regular lattice with control parameter 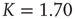and to dynamics of the ad hoc network evaluated for , respectively. In both cases 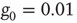. The dashed lines are visual guides corresponding to the scaling exponents 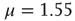and 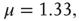respectively.

The statistical analysis of the real brain activity led some investigators [33–36] to conclude that the brain dynamics are dominated by renewal quakes (neuronal avalanches) and that the probability density of the time distance between two consecutive quakes has the inverse power-law index 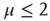. Theoretical arguments [37] establish that this condition is important for the cognitive brain function. On the basis of the plausible conjecture [31] that there is a close connection between the cooperative behavior of many elements and brain cognition, we believe that the emergence of the condition 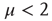from the interaction of the elements of the regular two-dimensional lattice is an important aspect of the dynamic approach to the scale-free condition.

On the other hand, the survival probability of the consensus state emerging from the ad hoc network, with 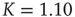, is limited to the time region 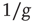, and for 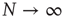is expected [11] to be dominated by the exponential shoulder depicted in Figure 24.5. The exponential shoulder is a signature of the equilibrium regime of the network dynamics [11].

24.5 Inflexible Minorities

Understanding the influence that committed minorities can exert on both local and global properties of complex networks is an issue of overwhelming importance. What are the conditions under which the convictions of an inflexible minority dominate the future behavior of a complex network? Turalska et al. [38] demonstrate that the abrupt changes in the organization of social groups such as described by DMM, rather than being moments of disorder, are instances of increased spatial correlation between the elements of the network. This condition of extended cooperation, similar to the critical state of a physical phase transition, allows a small subgroup of the society to exert substantial influence over the entire social network. One limiting case might be viewed as Carlyle's great man theory of history in On Heroes, Hero Worship, and the Heroes of History [39], where a single individual can change world opinion for better or worse.

A member of the committed minority considered herein is a randomly selected element at a node on the lattice that keeps its decision of either “yes” or “no” independently of the opinion of its neighbors. Thus, this element communicates an unchanging message to the rest of the network through its interactions. To establish that the committed minority may operate efficiently in spite of their small number, in Figure 24.6 we compare the evolution of 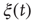in the absence of a committed minority to its evolution in the presence of a relatively small (1%) inflexible group. In the case considered here, values of the control parameter in excess of the critical value lead to the extended condition of global consensus. Turalska et al. [38] show that a rapidly decreasing correlation function reflects the rigidity of the network and prevents the global transmission of the perturbation. However, from time to time a crisis occurs where . In crisis, the network may undergo an abrupt change of opinion, and the correlation length may be sufficiently large to make it possible for the inflexible minority to force the social network to adopt their view. As a consequence, during the time interval over which the minority acts, it imposes its opinion over the entire network.

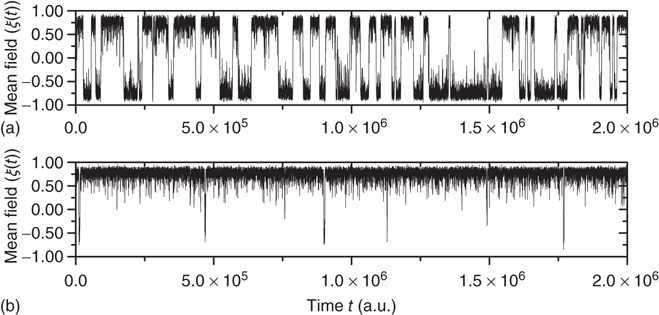
Figure 24.6 A small number of nodes maintaining constant opinion influence significantly the behavior of the system in the organized phase. (a) Fluctuations of the global order paramete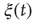r for 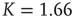and lattice of size 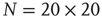nodes. (b) The behavior of 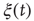once 1% of the randomly selected elements are kept in state “yes” at all times. Transition rate is 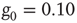for both.

Finally, to quantify the phenomenon of minority influence we study how introducing a committed minority affects the average lifetime of the consensus state, defined as

24.10

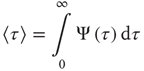
It is important to note that, when no committed group is present, the distribution of time durations of global decision in “yes,” 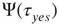, and in “no,” 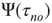, coincide and are equal to the distribution evaluated for both time intervals, 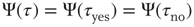. This symmetry is, however, broken once a minority is introduced, as shown in Figure 24.6 by an increase in temporal span of consensus states that correspond to the opinion of the minority.

In Figure 24.7 we compare 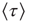in the absence of the inflexible agents to the average lifetime in the presence of a committed minority of sizes 1% and 5%. First, in the native case the average consensus time increases exponentially with an increase in the control parameter 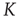, showing a faster rise once 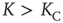, with a discontinuous change at the critical interaction strength. This switch in the rate of increase confirms the validity of the approach used to determine 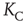based on the temporal properties of 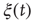. Consecutively, the introduction of a small minority leads to a linear increase in 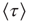, and the fact that two exponential regimes are preserved confirms the crucial role that instances of crisis play in the global transmission of minority opinion.

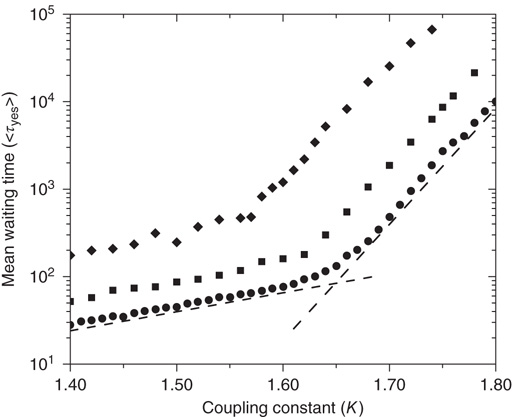
Figure 24.7 The mean waiting time obtained for a network with no acting minorities (dots) increases significantly once 1% (squares) or 5% (diamonds) committed minority is presented. Lattice size is nodes and .

It is also interesting to extend the committed minority results to the interaction between two complex networks. Suppose that the network 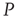consists of a group of zealots and that of 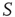the social group of interest. The dynamics of both 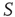and 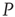are determined by the DMM. At a given point in time, a small number of nodes in network 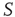are replaced by elements whose dynamics are determined by 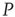, but otherwise they are allowed to interact with the elements of network 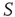. Figure 24.8 depicts three situations. In the upper panel, the dynamics of network 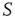with 400 elements on a two-dimensional lattice is shown in the absence of consensus. The center panel indicates the dynamics of network 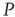with 400 elements on a two-dimensional lattice when the control parameter is above the critical value. In the bottom panel, the dynamics of the two networks are superposed when 5% of randomly positioned 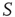elements are replaced with 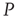elements. The newly replaced nodes retain their 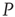-dynamics but are coupled in to the 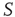-dynamics.

Figure 24.8 (a) The mean-field variable for network , a lattice with 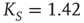; (b) The mean-field variable for network , a 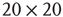lattice with 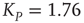; (c) The time series from the middle panel (black line) superposed on that of the 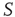network when 5% of the elements are replaced by those of 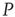(gray line).

It is evident that even this small number of elements from network 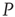(20) is sufficient to completely dominate the dynamics of network 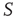. It is also interesting to determine what happens if the zealots in network 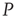are anarchists. We model an anarchist as advocating no particular opinion so that the control parameter of 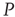is below the critical value and the zealot group appears random. Suppose further that network 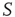was highly organized with a control parameter above the critical value, similar to the center panel of Figure 24.8. If the same replacement was made as was done in the above case, the well-defined switching between states would be lost and the social organization of network 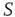would disintegrate. These interesting results are the topic of future investigations.

24.6 Conclusions

In summary, the self-organization of the DMM implemented on the two-dimensional network with 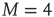generates a scale-free topology with 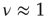as well as the long-range links essential for the collective mind of the network of self-organized elements of Couzin [31]. The exciting discovery of dynamic-hub neurons with 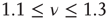[30] is a challenge for the dynamical derivation of the scale-free condition that is mainly confined to 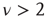[1, 5, 6], and it is remarkable that the approach used herein generates a power-law index in the range of the experimental results of Bonifazi et al. [30]. Wang et al. [40] use a weighted scale-free topology to promote or suppress synchronization. Here, these effects do not require a complex network structure. The DMM implemented on the DGCT networks shows the coexistence of two impenetrable [25] opinion clusters that develop independent decisions, with no influence of one cluster on the other. The regular topology generates time complexity, namely 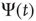with 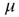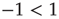, lasting for some decades, whereas the scale-free topology of the ad hoc networkgenerates consensus with a smaller control parameter 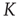, without yielding complexity in time. Aquino et al. [41] show that this kind of complex dynamical network shares the brain's sensitivity to 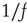noise. In short, the present research establishes that the scale-free distribution of links is a consequence of dynamic self-organization rather than being the cause of it.

Our approach does not allow us to confirm the observation made by Xie et al. [42] that the minimal size of the committed minority necessary to significantly affect the opinion of the entire network is 10%. We are convinced that difference in the size of the inflexible minority is a consequence of the interactions used in the two models. If we assume that a substantial effect of a committed minority is defined by an order of magnitude increase in the average consensus time, Figures 24.7 and 24.8 indicate that for DMM this requirement is realized by a committed minority of less than 5%. These considerations apparently generalize to the dynamic situation where the changes in the perturbing elements can dominate the dynamics of the host network.

References

1. 1. Albert, R. and Barabási, A. (2002) Statistical mechanics of complex networks. Rev. Mod. Phys., 74 (1), 47–97.
2. 2. Fraiman, D., Balenzuela, P., Foss, J., and Chialvo, D. (2009) Ising-like dynamics in large-scale functional brain networks. Phys. Rev. E, 79 (6), 061922.
3. 3. Watts, D. and Strogatz, S. (1998) Collective dynamics of “small-world” networks. Nature, 393, 440–442.
4. 4. Erds, P. and Rényi, A. (1960) On the evolution of random graphs. Magyar Tud. Akad. Mat. Kutató Int. Közl, 5, 17–61.
5. 5. Dorogovtsev, S. and Mendes, J. (2002) Evolution of networks. Adv. Phys., 51 (4), 1079–1187.
6. 6. Ferrer, R. and Sole, R. (2003) Optimalization in complex networks, in Statistical Mechanics of Complex Networks (eds R. Pastor-Satorras, M. Rubi, and A. Diaz-Guilera), Springer, Berlin, pp. 114–126.
7. 7. Baiesi, M. and Manna, S. (2003) Scale-free networks from a hamiltonian dynamics. Phys. Rev. E, 68 (4), 047103.
8. 8. Perotti, J., Billoni, O., Tamarit, F., Chialvo, D., and Cannas, S. (2009) Emergent self-organized complex network topology out of stability constraints. Phys. Rev. Lett., 103 (10), 108701.
9. 9. Beggs, J.M. and Plenz, D. (2003) Neuronal avalanches in neocortical circuits. J. Neurosci., 23 (35), 11167–11177.
10. 10. Bianco, S., Geneston, E., Grigolini, P., and Ignaccolo, M. (2008) Renewal aging as emerging property of phase synchronization. Physica A, 387 (5), 1387–1392.
11. 11. Turalska, M., Lukovic, M., West, B., and Grigolini, P. (2009) Complexity and synchronization. Phys. Rev. E, 80 (2), 021110.
12. 12. Turalska, M., West, B., and Grigolini, P. (2011) Temporal complexity of the order parameter at the phase transition. Phys. Rev. E, 83 (6), 061142.
13. 13. Arenas, A., Diaz-Guilera, A., Kurths, J., Moreno, Y., and Zhou, C. (2008) Synchronization in complex networks. Phys. Rep., 469 (3), 93–153.
14. 14. Castellano, C., Fortunato, S., and Loreto, V. (2009) Statistical physics of social dynamics. Rev. Mod. Phys., 81 (2), 591–646.
15. 15. Pikovsky, A., Rosenblum, M., and Kurths, J. (2003) Synchronization: A Universal Concept in Nonlinear Sciences, Vol. 12, Cambridge University Press.
16. 16. West, B., Geneston, E., and Grigolini, P. (2008) Maximizing information exchange between complex networks. Phys. Rep., 468 (1), 1–99.
17. 17. Onsager, L. (1944) Crystal statistics. I. A two-dimensional model with an order-disorder transition. Phys. Rev., 65 (3-4), 117–149.
18. 18. Plischke, M. and Bergersen, B. (eds) (2006) Equilibrium Statistical Physics, World Scientific Publishing Company Incorporated.
19. 19. McCoy, B. and Wu, T. (eds) (1973) The Two-Dimensional Ising Model, Harvard University Press.
20. 20. Turalska, M., Geneston, E., West, B., Allegrini, P., and Grigolini, P. (2012) Cooperation-induced topological complexity: a promising road to fault tolerance and hebbian learning. Front. Physiol., 3, 52.
21. 21. Kleinberg, J. (2000) Navigation in a small world. Nature, 406 (6798), 845.
22. 22. Boguna, M., Krioukov, D., and Claffy, K. (2008) Navigability of complex networks. Nat. Phys., 5 (1), 74–80.
23. 23. Boguna, M. and Krioukov, D. (2009) Navigating ultrasmall worlds in ultrashort time. Phys. Rev. Lett., 102 (5), 058701.
24. 24. Kalisky, T., Cohen, R., Ben-Avraham, D., Havlin, S, Ben-Naim, E., and Frauenfelder, H. (2004) in Tomography and stability of complex networks, in Complex Networks, Lecture Notes in Physics, (ed. Z. Toroczkai), Springer, Berline, pp. 3–34.
25. 25. Shao, J., Havlin, S., and Stanley, H. (2009) Dynamic opinion model and invasion percolation. Phys. Rev. Lett., 103 (1), 018701.
26. 26. Stam, C. (2004) Functional connectivity patterns of human magnetoencephalographic recordings: a'small-world'network? Neurosci. Lett., 355 (1-2), 25–28.
27. 27. Micheloyannis, S., Pachou, E., Stam, C., Vourkas, M., Erimaki, S., and Tsirka, V. (2006) Using graph theoretical analysis of multi channel EEG to evaluate the neural efficiency hypothesis. Neurosci. Lett., 402 (3), 273–277.
28. 28. Stam, C. and de Bruin, E. (2004) Scale-free dynamics of global functional connectivity in the human brain. Human Brain Mapp., 22 (2), 97–109.
29. 29. Eguiluz, V., Chialvo, D., Cecchi, G., Baliki, M., and Apkarian, A. (2005) Scale-free brain functional networks. Phys. Rev. Lett., 94 (1), 018102.
30. 30. Bonifazi, P., Goldin, M., Picardo, M., Jorquera, I., Cattani, A., Bianconi, G., Represa, A., Ben-Ari, Y., and Cossart, R. (2009) Gabaergic hub neurons orchestrate synchrony in developing hippocampal networks. Science, 326 (5958), 1419–1424.
31. 31. Couzin, I. (2007) Collective minds. Nature, 445 (7129), 715.
32. 32. Couzin, I. (2009) Collective cognition in animal groups. Trends Cogn. Sci., 13 (1), 36–43.
33. 33. Gong, P., Nikolaev, A., and van Leeuwen, C. (2007) Intermittent dynamics underlying the intrinsic fluctuations of the collective synchronization patterns in electrocortical activity. Phys. Rev. E, 76 (1), 011904.
34. 34. Bianco, S., Ignaccolo, M., Rider, M., Ross, M., Winsor, P., and Grigolini, P. (2007) Brain, music, and non-poisson renewal processes. Phys. Rev. E, 75 (6), 061911.
35. 35. Buiatti, M., Papo, D., Baudonniere, P., and van Vreeswijk, C. (2007) Feedback modulates the temporal scale-free dynamics of brain electrical activity in a hypothesis testing task. Neuroscience, 146 (3), 1400–1412.
36. 36. Allegrini, P., Menicucci, D., Bedini, R., Fronzoni, L., Gemignani, A., Grigolini, P., West, B., and Paradisi, P. (2009b) Spontaneous brain activity as a source of ideal 1/f noise. Phys. Rev. E, 80 (6), 061914.
37. 37. Grigolini, P., Aquino, G., Bologna, M., Lukovi, M., and West, B. (2009) A theory of 1/f noise in human cognition. Physica A, 388 (19), 4192–4204.
38. 38. Turalska, M., West, B. J., and Grigolini, P. (2013) Role of committed minorities in times of crisis. Scientific Reports 3, 1371.
39. 39. Carlyle, T. (1993) On Heroes, Hero-Worship, and the Heroic in History, Vol. 1, University of California Press.
40. 40. Wang, W., Huang, L., Lai, Y., and Chen, G. (2009) Onset of synchronization in weighted scale-free networks. Chaos, 19 (1), 013134.
41. 41. Aquino, G., Bologna, M., Grigolini, P., and West, B. (2010) Beyond the death of linear response: 1/f optimal information transport. Phys. Rev. Lett., 105 (4), 040601.
42. 42. Xie, J., Sreenivasan, S., Korniss, G., Zhang, W., Lim, C., and Szymanski, B. (2011) Social consensus through the influence of committed minorities. Phys. Rev. E, 84 (1), 011130.