
Here is a question you may have at this point that I want to deal with it:
You showed me the machine code in Fig 1.6.2 and said that is what the computer understands, but I've always heard that computers understand 1’s and 0’s. That machine code does not look like 1’s and 0’s. What's the deal?
Okay. A computer chip (or CPU) at their most microscopic, fascinating, magical, mind-boggling, yet also slightly boring level are made from billions of almost unimaginably tiny electrical switches, each one either ON or Off.
If I could take a CPU and scan it with an electron microscope (there are videos on YouTube where people actually do this) and zoom in and zoom in and zoom in, we would eventually get to millions or billions of these tiny electrical switches or transistors on the chip. Each one is closed or open (on or off).

Fig 1.8.1: The inside of a microchip. Here, we zoom into a microchip using a digital SLR camera then we transition to a scanning electron microscope
To be clear to be a successful program and you don't have to know anything about CPUs, integrated circuits, transistors or capacitors or buy stable flip flops. That's hardware. We are dealing with software, a different skillset, like a surgeon who needs to know how to use a scalpel or an EKG machine, but they don't need to know how to make one.
What is good is to know enough about a CPU that we don't just think it's a bunch of magical leprechauns making our programs work. There is way more to a modern CPU than just lots of transistors, but still it's different combinations of these switches.
There are different groupings and arrangements of transistors that are used by the CPU together with other parts of our computer, like memory modules, to represent number values and texts, hold graphics and audio, and all the programs you're running at any moment and exactly what they're all doing right now. Yes, that can seem puzzling. It isn't immediately obvious how we can take a bunch of tiny on/off switches and say this bunch of switches is a picture of an alien spaceship.
Well, okay, I can’t show billions of switches. So, let's begin with one.

Fig 1.8.2: Left switch is in ON position; Right switch is in OFF position
I'll use this symbol for a toggle switch, that is, a switch that is either on or off.
The important thing here is not whether this is connected to something or causes something to happen elsewhere. No, it's the switch itself just by itself because I can decide what I want it to mean and what it represents is up to me. It can be different in my program than in yours, as long as what it represents only has two options.
In a computer program, I might decide that this means a user is either logged in or not logged in.
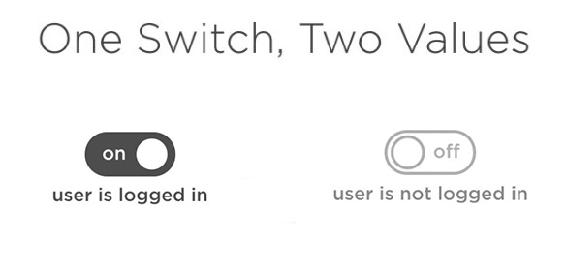
Fig 1.8.3: ON switch represents user is logged in while OFF switch represents user is not logged in
I could use another switch to say we are currently recording or we are currently not recording. But what I can't use a switch for is anything more complex. I can’t use one switch to represent a bank balance or the result of a horse race or a PDF invoice, but I can add more switches. I can group them together because we have a ridiculous amount of them available.
If I have a group of two switches, I go from two possible values to four possible values as shown in Fig 1.8.4.

Fig 1.8.4: Four possible values obtained from two switches
Okay fine. This is very simple because whenever I add a switch, I'm not just adding two additional options (not just another on off) I'm actually doubling the amount of values we can hold. Maybe when we go from just one to two switches, it's unimpressive.
So, let’s take this further. If I add one more switch (switch 3), I'd go from four to eight possible arrangements of three switches. See Fig 1.8.4.
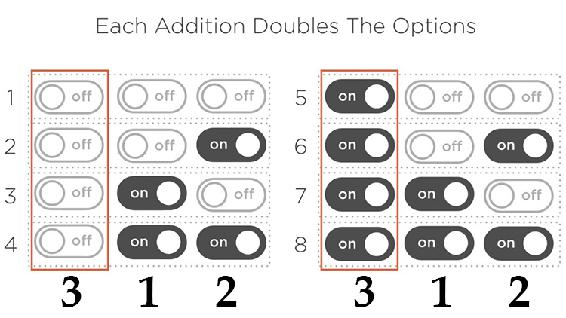
Fig 1.8.5: Eight possible values obtained from 3 switches
Every time I add one switch, I double the possible values, that is, all the arrangements from before with the new switch off as well as all the arrangements from before with the new switch on. So, it rapidly increases, always doubling. With 3 switches it's 8 possible arrangements. With 4 switches we have 16 values or arrangements.

Fig 1.8.6: Sixteen possible values obtained from four switches
With 5 switches we have 32, and with 6 switches we have 64 values. When we have just 8 switches, there are already 256 possible arrangements of these, from all of them OFF, all of them ON and everything in between.
I've been using these toggles switch icons, but these are getting to the end of their usefulness. I can't really fit anymore. But I still need a way to describe these arrangements. I could use words to represent them (such as off, on, off, on, off… etc), but that's kind of clunking.