Now what we can do is use a 0 for an OFF and a 1 for an ON. This is a very compact and concise way to do this. It is actually 0s and 1s we use in computing. It is called the binary code.
We use the binary code as a way to represent that most basic, most fundamental state of just part of a computer. There aren't really zeros and ones bouncing around inside your computer. They are just ways we can represent or visualize those tiny elements being on or off.
Now let me correct myself. I've been calling them a switch, but in computing we don't call each of these elements a switch. We call it a bit for binary digit. The tiniest element of information that is either 0 or 1.
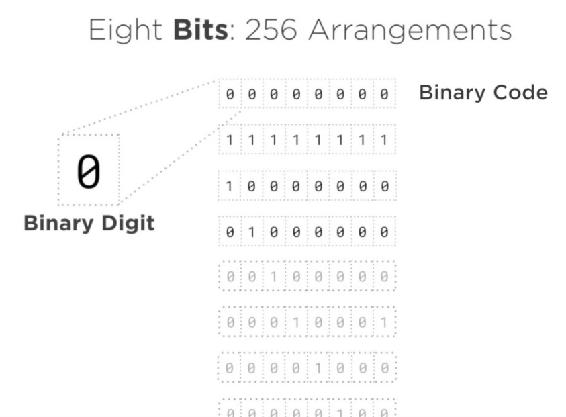
So, in the example shown in Fig 1.9.1, I have 8 bits, which gives me 256 possible arrangements from all 0’s at the top, to all 1’s and everything in between.

Fig 1.9.1: An 8-bit binary code for 256 values
So, I could use a group of 8 bits and decide it represents some modest number. For example, suppose I need to keep track of perhaps the amount of enemies on my screen. As long as I know that number never needs to be more than 256, an 8-bit binary code is all I need to keep track of it.
If I need to store bigger values, I add more bits. Because computers really are built on this binary idea, it is easier to deal in multiples of two. If I go from 8 bit to 16 bit we will go from 256 to about 65,000 possible values. Double it again to 32 bits, we're already at 4.3 billion possible values! With 64 bits, well I don't know how to say this, but it's a lot!

Fig 1.9.2: Getting bigger values by doubling the bits