L’élément génétique idéal de la courbure variable, ou du pli, c’est l’inflexion. L’inflexion est le véritable atome, le point élastique. C’est elle que Klee dégage comme l’élément génétique de la ligne active, spontanée, témoignant ainsi de son affinité avec le Baroque et avec Leibniz, s’opposant à Kandinsky, cartésien, pour qui les angles sont durs, le point est dur, mis en mouvement par une force extérieure. Mais, pour Klee, le point comme « concept non conceptuel de la non-contradiction » parcourt une inflexion. Il est le point d’inflexion lui-même, là où la tangente traverse la courbe. C’est le point-pli. Klee commence par une succession de trois figures1. La première dessine l’inflexion. Le seconde montre qu’il n’y a pas de figure exacte et sans mélange, comme disait Leibniz, pas « de droite sans courbures entremêlées », mais aussi pas « de courbe d’une certaine nature finie sans mélange de quelque autre, et cela dans les plus petites parties comme dans les plus grandes », si bien qu’on « ne pourra jamais assigner à quelque corps une certaine surface précise, comme on pourrait faire s’il y avait des atomes »2. La troisième marque d’ombre le côté convexe, et dégage ainsi la concavité et son centre de courbure, qui changent de côté de part et d’autre du point d’inflexion.
Bernard Cache définit l’inflexion, ou le point d’inflexion, comme une singularité intrinsèque. Contrairement aux « extrema » (singularités extrinsèques, maximum et minimum), elle ne renvoie pas à des coordonnées : elle n’est ni en haut ni en bas, ni à droite ni à gauche, ni régression ni progression. Elle correspond à ce que Leibniz appelle un « signe ambigu ». Elle est en apesanteur ; même les vecteurs de concavité n’ont rien à voir encore avec un vecteur de gravité, puisque les centres de courbure qu’ils déterminent oscillent autour d’elle. Aussi l’inflexion est-elle le pur Événement, de la ligne ou du point, le Virtuel, l’idéalité par excellence. Elle s’effectuera d’après des axes de coordonnées, mais pour le moment elle n’est pas dans le monde : elle est le Monde lui-même, ou plutôt son commencement, disait Klee, « lieu de la cosmogenèse », « point non dimensionnel », « entre les dimensions ». Un événement qui serait attente d’événement ? C’est à ce titre qu’elle passe déjà par des transformations possibles, trois sortes de transformations selon Cache3.
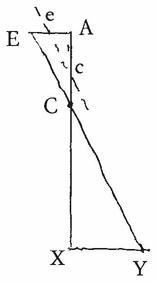
Ligne active prenant librement ses ébats. Promenade pour la promenade, sans but particulier. Agent : un point en mouvement (fig. 1) :
Cette même ligne avec des formes d’accompagnement (fig. 2 et 3) :


Les premières sont vectorielles, ou par symétrie, avec un plan de réflexion orthogonal ou tangent. Elles opèrent suivant les lois optiques, et transforment l’inflexion en point de rebroussement, ou en ogive. L’ogive exprime la forme d’un mobile qui épouse la configuration des lignes d’écoulement du fluide, et le rebroussement, le profil d’un fond de vallée quand les eaux se rangent sous l’unité d’un seul cours :

Les secondes transformations sont projectives : elles expriment la projection, sur l’espace externe, d’espaces internes définis par des « paramètres cachés » et des variables ou singularités de potentiel. Les transformations de Thom renvoient en ce sens à une morphologie du vivant, et donnent les sept événements élémentaires : le pli, la fronce, la queue d’aronde, le papillon, l’ombilic hyperbolique, elliptique, parabolique4.
Enfin, l’inflexion en elle-même est inséparable d’une variation infinie ou d’une courbure infiniment variable. C’est la courbe de Koch, qu’on obtient à force d’arrondir les angles d’après l’exigence baroque, en les faisant proliférer suivant une loi d’homothétie : elle passe par un nombre infini de points anguleux et n’admet de tangente en aucun de ces points, elle enveloppe un monde infiniment spongieux ou caverneux, elle constitue plus qu’une ligne et moins qu’une surface (la dimension fractale de Mandelbrot comme nombre fractionnaire ou irrationnel, non-dimension, inter-dimension5). Encore l’homothétie fait-elle coïncider la variation avec un changement d’échelle, comme dans le cas de la longueur d’une côte géographique. Tout change lorsque l’on fait intervenir la fluctuation plutôt que l’homothétie interne. Ce n’est plus la possibilité de déterminer un point anguleux entre deux autres si rapprochés soient-ils, mais la latitude d’ajouter toujours un détour, en faisant de tout intervalle le lieu d’un nouveau plissement. C’est là qu’on va de pli en pli, non pas de point en point, et que tout contour s’estompe au profit des puissances formelles du matériau, qui montent à la surface et se présentent comme autant de détours et de replis supplémentaires. La transformation de l’inflexion n’admet plus de symétrie, ni de plan privilégié de projection. Elle devient tourbillonnaire, et se fait par retard, par différé, plutôt que par prolongement ou prolifération : la ligne en effet se replie en spirale pour différer l’inflexion dans un mouvement suspendu entre ciel et terre, qui s’éloigne ou se rapproche indéfiniment d’un centre de courbure, et, à chaque instant, « prend son envol ou risque de s’abattre sur nous »6. Mais la spirale verticale ne retient pas, ne diffère pas l’inflexion, sans la promettre aussi et la rendre irrésistible, en transversale : une turbulence ne se produit jamais seule, et sa spirale suit un mode de constitution fractal selon lequel de nouvelles turbulences s’intercalent toujours entre les premières7. C’est la turbulence qui se nourrit de turbulences, et, dans l’effacement du contour, ne se termine qu’en écume ou crinière. C’est l’inflexion même qui devient tourbillonnaire, en même temps que sa variation s’ouvre à la fluctuation, devient fluctuation.
La définition des mathématiques baroques apparaît avec Leibniz : elles prennent pour objet une « nouvelle affection » des grandeurs variables, qui est la variation même. En effet, dans un nombre fractionnaire ou même dans une formule algébrique, ce n’est pas la variabilité qui est considérée comme telle, puisque chacun des termes a ou doit avoir une valeur particulière. Il n’en est plus ainsi pour le nombre irrationnel et le calcul des séries qui lui correspond, pour le quotient différentiel et le calcul des différences, où la variation devient actuellement infinie, le nombre irrationnel étant la limite commune de deux séries convergentes dont l’une n’a pas de maximum et l’autre pas de minimum, le quotient différentiel étant la limite commune du rapport entre deux quantités en train de s’évanouir. Mais on remarquera, dans les deux cas, la présence d’un élément de courbure agissant comme cause. Le nombre irrationnel implique la chute d’un arc de cercle sur la ligne droite des points rationnels, et dénonce celle-ci comme un faux infini, simple indéfini comportant une infinité de lacunes ; c’est pourquoi le continu est un labyrinthe, et ne peut être représenté par une ligne droite, toujours la droite devant être entremêlée de courbures.
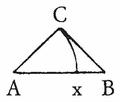
Entre deux points A et B si rapprochés soient-ils, il y a toujours possibilité de mener le triangle rectangle isocèle dont l’hypoténuse va de A à B, et dont le sommet C détermine un cercle qui recoupe la droite entre A et B. L’arc de cercle est comme une branche d’inflexion, élément de labyrinthe, qui fait du nombre irrationnel, à la rencontre de la courbe et de la droite, un point-pli. Il en est de même pour le quotient différentiel, avec le point-pli A qui garde le rapport c/e quand ces deux grandeurs s’évanouissent (c’est aussi bien le rapport entre un rayon et une tangente qui convient à l’angle en C)8. Bref, il y a toujours une inflexion qui fait de la variation un pli, et qui porte le pli ou la variation à l’infini. Le pli, c’est la Puissance, comme on le voit dans le nombre irrationnel qui passe par une extraction de racine, et dans le quotient différentiel qui passe par le rapport d’une grandeur et d’une puissance, comme condition de la variation. La puissance elle-même est acte, c’est l’acte du pli.
Quand les mathématiques prennent pour objet la variation, c’est la notion de fonction qui tend à se dégager, mais aussi la notion d’objet change et devient fonctionnelle. Dans des textes mathématiques particulièrement importants, Leibniz pose l’idée d’une famille de courbes dépendant d’un ou plusieurs paramètres : « Au lieu de chercher la droite unique tangente en un point unique à une courbe donnée, on se donne à chercher la courbe tangente en une infinité de points à une infinité de courbes ; la courbe n’est pas touchée, elle est touchante, la tangente n’est plus ni droite ni unique ni touchante, elle devient courbe, famille infinie, touchée » (problème de l’inverse des tangentes)9. Il y a donc une série de courbes qui n’impliquent pas seulement des paramètres constants, pour chacune et pour toutes, mais la réduction des variables à « une seule et unique variabilité » de la courbe touchante ou tangente : le pli. L’objet ne se définit plus par une forme essentielle, mais atteint à une fonctionnalité pure, comme déclinant une famille de courbes encadrées par des paramètres, inséparable d’une série de déclinaisons possibles ou d’une surface à courbure variable qu’il décrit lui-même. Appelons objectile ce nouvel objet. Comme le montre Bernard Cache, c’est une conception très moderne de l’objet technologique : elle ne renvoie même pas aux débuts de l’ère industrielle où l’idée du standard maintenait encore un semblant d’essence et imposait une loi de constance (« l’objet produit par les masses et pour les masses »), mais à notre situation actuelle, quand la fluctuation de la norme remplace la permanence d’une loi, quand l’objet prend place dans un continuum par variation, quand la productique ou la machine à commande numérique se substituent à l’emboutissage. Le nouveau statut de l’objet ne rapporte plus celui-ci à un moule spatial, c’est-à-dire à un rapport forme-matière, mais à une modulation temporelle qui implique une mise en variation continue de la matière autant qu’un développement continu de la forme. Dans la modulation, « il n’y a jamais arrêt pour démoulage, parce que la circulation du support d’énergie équivaut à un démoulage permanent ; un modulateur est un moule temporel continu... Mouler est moduler de manière définitive, moduler est mouler de manière continue et perpétuellement variable »10. N’est-ce pas la modulation que Leibniz définit en disant que la loi de la série pose les courbes comme « la trace de la même ligne » en mouvement continu, continuellement touchée par la courbe de leur concours ? C’est une conception non seulement temporelle, mais qualitative de l’objet, pour autant que les sons, les couleurs, sont flexibles et pris dans la modulation. C’est un objet maniériste, et non plus essentialiste : il devient événement.
Si l’objet change profondément de statut, le sujet aussi. Nous passons de l’inflexion ou de la courbure variable aux vecteurs de courbure du côté de la concavité. Partant d’une branche de l’inflexion, nous déterminons un point qui n’est plus celui qui parcourt l’inflexion, ni le point d’inflexion même, mais celui où se rencontrent les perpendiculaires aux tangentes dans un état de la variation. Ce n’est pas exactement un point, mais un lieu, une position, un site, un « foyer linéaire », ligne issue de lignes.

On l’appelle point de vue pour autant qu’il représente la variation ou inflexion. Tel est le fondement du perspectivisme. Celui-ci ne signifie pas une dépendance à l’égard d’un sujet défini au préalable : au contraire, sera sujet ce qui vient au point de vue, ou plutôt ce qui demeure au point de vue. C’est pourquoi la transformation de l’objet renvoie à une transformation corrélative du sujet : le sujet n’est pas un sub-jet, mais un « superjet », comme dit Whitehead. En même temps que l’objet devient objectile, le sujet devient superjet. Entre la variation et le point de vue il y a un rapport nécessaire : non pas simplement en raison de la variété des points de vue (bien qu’il y ait une telle variété, nous le verrons), mais en premier lieu parce que tout point de vue est point de vue sur une variation. Ce n’est pas le point de vue qui varie avec le sujet, du moins en premier lieu ; il est au contraire la condition sous laquelle un éventuel sujet saisit une variation (métamorphose), ou quelque chose = x (anamorphose)11. Le perspectivisme chez Leibniz, et aussi chez Nietzsche, chez William et chez Henry James, chez Whitehead, est bien un relativisme, mais ce n’est pas le relativisme qu’on croit. Ce n’est pas une variation de la vérité d’après le sujet, mais la condition sous laquelle apparaît au sujet la vérité d’une variation. C’est l’idée même de la perspective baroque.
On objecte pourtant que le point de vue saute, avec le côté de la concavité : n’y a-t-il pas contradiction entre la continuité de la variation infinie et la discontinuité du point de vue, et n’est-ce pas la même contradiction que beaucoup d’auteurs (à la suite de Kant) dénonceront chez Leibniz entre la loi de continuité et le principe des indiscernables ? Il n’en est rien, si l’on s’efforce dès le début de ne pas confondre continuité et contiguïté12. Les singularités, les points singuliers appartiennent pleinement au continu, bien qu’ils ne soient pas contigus. Les points d’inflexion constituent une première sorte de singularités dans l’étendue, et déterminent des plis qui entrent dans la mesure de la longueur des courbes (plis de plus en plus petits...). Les points de vue sont une seconde sorte de singularités dans l’espace, et constituent des enveloppes suivant des rapports indivisibles de distance. Mais pas plus les uns que les autres ne contredisent au continu : il y a autant de points de vue, dont la distance est chaque fois indivisible, qu’il y a d’inflexions dans l’inflexion, dont la longueur est de plus en plus grande. Le continu est fait de distances entre points de vue, non moins que de la longueur d’une infinité de courbes correspondantes. Le perspectivisme est bien un pluralisme, mais implique à ce titre la distance et non la discontinuité (certes il n’y a pas de vide entre deux points de vue). Leibniz peut définir l’étendue (extensio) comme « la répétition continue » du situs ou de la position, c’est-à-dire du point de vue : non pas que l’étendue soit alors l’attribut du point de vue, mais elle est l’attribut de l’espace (spatium) comme ordre des distances entre points de vue, qui rend cette répétition possible13.
Le point de vue sur une variation vient remplacer le centre d’une figure ou d’une configuration. L’exemple le plus célèbre est celui des coniques, où la pointe du cône est le point de vue auquel on rapporte le cercle, l’ellipse, la parabole, l’hyperbole, et même la droite et le point, comme autant de variantes d’après l’inclinaison du plan de coupe (« scénographies »). Toutes ces figures deviennent autant de manières dont se plie un « géométral ». Et ce géométral n’est pas exactement le cercle, qui ne devrait un tel privilège qu’à la vieille conception de la perspective, mais bien l’objectile qui décline ou décrit maintenant une famille de courbes, celles du second degré dont le cercle fait partie. Cet objectile, ou géométral, est comme un dépli. Mais le dépli n’est pas le contraire des plis, pas plus que l’invariant n’est le contraire de la variation : c’est un invariant de transformation. Il sera désigné par un « signe ambigu »14. En effet, il est enveloppé dans la variation, comme la variation est enveloppée dans le point de vue. Il n’existe pas hors de la variation, comme la variation n’existe pas hors du point de vue. C’est pourquoi, à la base de cette nouvelle théorie des coniques, Desargues nommait « involution » le rapport ou la loi enveloppés par une variation (par exemple, un triangle étant supposé tourner autour d’un axe, les dispositions des points définis sur l’axe par la projection des trois sommets et par le prolongement des trois côtés)15.
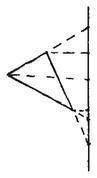
Nul mieux que Michel Serres n’a dégagé les conséquences, mais aussi les présupposés de la nouvelle théorie des coniques : dans un monde de l’infini, ou de la courbure variable, qui a perdu tout centre, l’importance de substituer le point de vue au centre défaillant ; le nouveau modèle optique de la perception, et de la géométrie dans la perception, qui répudie les notions tactiles, contact et figure, au profit d’une « architecture de la vision » ; le statut de l’objet, qui n’existe plus qu’à travers ses métamorphoses ou dans la déclinaison de ses profils ; le perspectivisme comme vérité de la relativité (et non relativité du vrai). C’est que le point de vue est dans chaque domaine de variation puissance d’ordonner les cas, condition de la manifestation du vrai : ainsi la série alternée des coniques à partir du sommet du cône (point fini, droite infinie, cercle fini, parabole infinie, ellipse finie, hyperbole infinie), ou bien la série des puissances de 2 à partir du sommet du triangle arithmétique, et pour tout domaine la nécessité d’assigner le point de vue sans lequel on ne peut trouver la vérité, c’est-à-dire sérier la variation ou déterminer les cas16. Dans tous les domaines, Leibniz construit la « table » des cas qui renvoie au point de vue comme jurisprudence ou art de juger. Toujours trouver le bon point de vue, ou plutôt le meilleur, sans lequel il n’y aurait que désordre et même chaos. Quand nous invoquions Henry James, c’était suivant l’idée leibnizienne du point de vue comme secret des choses, foyer, cryptographie, ou bien comme détermination de l’indéterminé par des signes ambigus : cela dont je vous parle, et à quoi vous pensez aussi, êtes-vous d’accord pour le dire de lui, à condition qu’on sache à quoi s’en tenir, sur elle, et qu’on soit d’accord aussi sur qui est lui, et qui est elle ? Seul un point de vue nous donne les réponses et les cas, comme dans une anamorphose baroque.
Nous sommes passés de la courbure variable au foyer de courbure (du côté concave), de la variation au point de vue, du pli à l’enveloppement, bref, de l’inflexion à l’inclusion. La transition est insensible, un peu comme l’angle droit ne se mesure pas par un grand arc, mais par un arc si petit soit-il et si rapproché du sommet : c’est déjà dans le sommet « que se trouve l’angle ou l’inclinaison des deux lignes »17. Pourtant on hésite à dire que le visible est dans le point de vue. Il faudrait une intuition plus naturelle pour nous faire admettre ce passage à la limite. Or c’est une intuition très simple : pourquoi quelque chose serait-il plié, sinon pour être enveloppé, mis dans autre chose ? Il apparaît que l’enveloppe prend ici son sens ultime, ou plutôt final : ce n’est plus une enveloppe de cohérence ou de cohésion, comme l’œuf, dans l’« enveloppement réciproque » des parties organiques. Mais pas davantage une enveloppe mathématique d’adhérence ou d’adhésion, où c’est encore un pli qui enveloppe des plis, comme dans l’enveloppante qui touche une infinité de courbes en une infinité de points. C’est une enveloppe d’inhérence ou d’« inhésion » unilatérale : l’inclusion, l’inhérence, est la cause finale du pli, si bien qu’on passe insensiblement de celui-ci à celle-là. Entre les deux un décalage s’est produit, qui fait de l’enveloppe la raison du pli : ce qui est plié, c’est l’inclus, l’inhérent. On dira que ce qui est plié est seulement virtuel, et n’existe actuellement que dans une enveloppe, dans quelque chose qui l’enveloppe.
Dès lors, ce n’est pas exactement le point de vue qui inclut ; ou du moins, il ne le fait qu’à titre d’agent, mais non de cause finale ou d’acte achevé (entéléchie). L’inclusion, l’inhérence, a une condition de clôture ou de fermeture que Leibniz énonce dans sa formule célèbre, « pas de fenêtres », et que le point de vue ne suffit pas à remplir. Ce dans quoi l’inclusion est faite, et ne cesse d’être faite, ou ce qui inclut au sens d’acte achevé, ce n’est pas le site ou le lieu, ce n’est pas le point de vue, mais ce qui demeure au point de vue, ce qui occupe le point de vue, et sans quoi le point de vue n’en serait pas un. C’est nécessairement une âme, un sujet. C’est toujours une âme qui inclut ce qu’elle saisit de son point de vue, c’est-à-dire l’inflexion. L’inflexion est une idéalité ou virtualité qui n’existe actuellement que dans l’âme qui l’enveloppe. Aussi est-ce l’âme qui a des plis, qui est pleine de plis. Les plis sont dans l’âme, et n’existent actuellement que dans l’âme. C’est déjà vrai des « idées innées » : ce sont de pures virtualités, de pures puissances, dont l’acte consiste en habitus ou dispositions (plis) dans l’âme, et dont l’acte achevé consiste en une action intérieure de l’âme (déploiement interne)18. Mais ce n’est pas moins vrai du monde : le monde entier n’est qu’une virtualité qui n’existe actuellement que dans les plis de l’âme qui l’exprime, l’âme opérant des déplis intérieurs par lesquels elle se donne une représentation du monde incluse. Nous allons de l’inflexion à l’inclusion dans un sujet, comme du virtuel à l’actuel, l’inflexion définissant le pli, mais l’inclusion définissant l’âme ou le sujet, c’est-à-dire ce qui enveloppe le pli, sa cause finale et son acte achevé.
D’où la distinction de trois sortes de points, comme trois sortes de singularités19. Le point physique est celui qui parcourt l’inflexion ou le point d’inflexion lui-même : ce n’est ni un atome ni un point cartésien, mais un point-pli, élastique ou plastique. Aussi n’est-il pas exact. Mais l’important, c’est que, d’une part, il dévalorise le point exact, d’autre part il entraîne le point mathématique à prendre un nouveau statut, rigoureux sans être exact. D’une part, en effet, le point exact n’est pas une partie de l’étendue, mais une extrémité conventionnelle de la ligne. D’autre part, le point mathématique perd de l’exactitude à son tour, pour devenir position, site, foyer, lieu, lieu de conjonction des vecteurs de courbure, bref, point de vue. Celui-ci prend donc une valeur génétique : la pure étendue sera la continuation ou la diffusion du point, mais suivant les rapports de distance qui définissent l’espace (entre deux points quelconques) comme « lieu de tous les lieux ». Pourtant, si le point mathématique cesse d’être ainsi l’extrémité de la ligne pour devenir l’intimité du foyer, il n’en reste pas moins une simple « modalité ». Il est dans le corps, dans la chose étendue20. Mais à ce titre, nous l’avons vu, il est seulement la projection d’un troisième point dans le corps. C’est le point métaphysique, l’âme ou le sujet, ce qui occupe le point de vue, ce qui se projette dans le point de vue. Aussi l’âme n’est-elle pas dans un corps en un point, mais est elle-même un point supérieur et d’une autre nature qui correspond avec le point de vue. On distinguera donc le point d’inflexion, le point de position, le point d’inclusion.
On sait quel nom Leibniz donnera à l’âme ou au sujet comme point métaphysique : monade. Il emprunte ce nom aux néoplatoniciens, qui s’en servaient pour désigner un état de l’Un : l’unité en tant qu’elle enveloppe une multiplicité, cette multiplicité développant l’Un à la façon d’une « série »21. Plus exactement l’Un a une puissance d’enveloppement et de développement, tandis que le multiple est inséparable des plis qu’il fait quand il est enveloppé, et des déplis, quand il est développé. Mais ainsi les enveloppements et développements, les implications et les explications, sont encore des mouvements particuliers qui doivent être compris dans une universelle Unité qui les « complique » tous, et complique tous les Uns. C’est Bruno qui portera le système des monades au niveau de cette complication universelle : Âme du monde qui complique tout. Les émanations néo-platoniciennes font donc place à une large zone d’immanence, même si les droits d’un Dieu transcendant ou d’une Unité encore supérieure sont formellement respectés. Expliquer-impliquer-compliquer forment la triade du pli, suivant les variations du rapport Un-multiple22. Mais si l’on demande pourquoi le nom de monade est resté lié à Leibniz, c’est que de deux façons Leibniz allait en fixer le concept. D’une part, les mathématiques de l’inflexion lui permettaient de poser la série du multiple comme série convergente infinie. D’autre part, la métaphysique de l’inclusion lui permettait de poser l’unité enveloppante comme unité individuelle irréductible. En effet, tant que les séries restaient finies ou indéfinies, les individus risquaient d’être relatifs, appelés à se fondre dans un esprit universel ou une âme du monde capable de compliquer toutes les séries. Mais, si le monde est une série infinie, il constitue à ce titre la compréhension logique d’une notion ou d’un concept qui ne peut plus être qu’individuel, il est donc enveloppé par une infinité d’âmes individuées dont chacune garde son point de vue irréductible. C’est l’accord des points de vue singuliers, ou l’harmonie, qui remplacera l’universelle complication, et conjurera les dangers de panthéisme ou d’immanence : d’où l’insistance de Leibniz à dénoncer l’hypothèse, ou plutôt l’hypostase d’un Esprit universel, qui ferait de la complication une opération abstraite où s’abîmeraient les individus23.
Tout ceci reste obscur. Car si Leibniz, poussant jusqu’au bout une métaphore esquissée par Plotin, fait de la monade une sorte de point de vue sur la ville, faut-il comprendre qu’une certaine forme correspond à chaque point de vue24 ? Par exemple une rue de telle ou telle forme ? Dans les coniques, il n’y a pas un point de vue auquel renverrait l’ellipse, et un autre pour la parabole, un autre pour le cercle. Le point de vue, le sommet du cône, est la condition sous laquelle on saisit l’ensemble de la variation des formes ou la série des courbes du second degré. Il ne suffit même pas de dire que le point de vue saisit une perspective, un profil qui présenterait chaque fois toute la ville à sa manière. Car il fait apparaître aussi la connexion de tous les profils entre eux, la série de toutes les courbures ou inflexions. Ce qui est saisi d’un point de vue, ce n’est donc ni une rue déterminée ni son rapport déterminable avec les autres rues, qui sont des constantes, mais la variété de toutes les connexions possibles entre parcours d’une rue quelconque à une autre : la ville en tant que labyrinthe ordonnable. La série infinie des courbures ou inflexions, c’est le monde, et le monde entier est inclus dans l’âme sous un point de vue.
Le monde est la courbe infinie qui touche en une infinité de points une infinité de courbes, la courbe à variable unique, la série convergente de toutes les séries. Mais alors pourquoi n’y a-t-il pas un seul point de vue universel, pourquoi Leibniz nie-t-il avec tant de force « la doctrine d’un esprit universel » ? Pourquoi y a-t-il plusieurs points de vue et plusieurs âmes irréductibles, une infinité ? Considérons la série des douze sons : elle est susceptible à son tour de beaucoup de variations, non seulement rythmiques et mélodiques, mais suivant le mouvement contraire, ou le mouvement rétrograde. À plus forte raison une série infinie, même si la variable est unique, est inséparable d’une infinité de variations qui la constituent : on la prend nécessairement suivant tous les ordres possibles, et l’on privilégie tour à tour telle ou telle séquence partielle. C’est là seulement qu’une forme, une rue, reprend ses droits, mais par rapport à la série tout entière : chaque monade comme unité individuelle inclut toute la série, elle exprime ainsi le monde entier, mais ne l’exprime pas sans exprimer plus clairement une petite région du monde, un « département », un quartier de la ville, une séquence finie. Deux âmes n’ont pas le même ordre, mais n’ont pas non plus la même séquence, la même région claire ou éclairée. On dira même que, dans la mesure où l’âme est pleine de plis à l’infini, elle peut toutefois en déplier un petit nombre à l’intérieur de soi, ceux qui constituent son département ou son quartier25. On n’y verra pas encore une définition de l’individuation : s’il n’existe que des individus, ce n’est pas parce qu’ils incluent la série dans un certain ordre et d’après telle région, c’est même l’inverse. Aussi n’avons-nous pour le moment qu’une définition nominale de l’individu. Elle suffit toutefois à montrer qu’il y a nécessairement une infinité d’âmes et une infinité de points de vue, bien que chaque âme inclue et que chaque point de vue saisisse la série infiniment infinie. Chacun la saisit ou l’inclut dans un ordre et suivant un quartier différents. Revenons au schéma élémentaire des deux foyers de l’inflexion : en vérité, chacun d’eux est un point de vue sur l’inflexion tout entière, mais c’est dans un ordre inverse (mouvement rétrograde) et suivant un département opposé (l’une des deux branches).
Mais pourquoi faut-il partir du monde ou de la série ? Sinon le thème du miroir et du point de vue perdrait tout sens. Nous allons des inflexions du monde à l’inclusion dans des sujets : comment est-ce possible, puisque le monde n’existe que dans des sujets qui l’incluent ? Ce sont les premières lettres à Arnauld qui détaillent la conciliation de deux propositions essentielles à cet égard. D’une part, le monde où Adam a péché n’existe que dans Adam pécheur (et dans tous les autres sujets qui composent ce monde). D’autre part, Dieu crée, non pas Adam pécheur, mais le monde où Adam a péché. En d’autres termes, si le monde est dans le sujet, le sujet n’en est pas moins pour le monde. Dieu produit le monde « avant » de créer les âmes, puisqu’il les crée pour ce monde qu’il met en elles. C’est même en ce sens que la loi de la série infinie, la « loi des courbures », n’est pas dans l’âme, bien que la série le soit, bien que les courbures y soient. C’est en ce sens aussi que l’âme est une « production », un « résultat » : elle résulte du monde que Dieu a choisi. Parce que le monde est dans la monade, chacune inclut toute la série des états du monde ; mais, parce que la monade est pour le monde, aucune ne contient clairement la « raison » de la série, dont elles résultent toutes, et qui leur reste extérieure comme le principe de leur accord26. On va donc du monde au sujet, au prix d’une torsion qui fait que le monde n’existe actuellement que dans les sujets, mais aussi que les sujets se rapportent tous à ce monde comme à la virtualité qu’ils actualisent. Lorsque Heidegger s’efforce de dépasser l’intentionnalité comme détermination trop empirique encore du rapport sujet-monde, il pressent que la formule leibnizienne de la monade sans fenêtres est une voie de ce dépassement, puisque le Dasein, dit-il, est déjà ouvert de tout temps et n’a pas besoin de fenêtres par lesquelles une ouverture lui adviendrait. Mais ainsi il méconnaît la condition de clôture ou de fermeture énoncée par Leibniz, c’est-à-dire la détermination d’un être-pour le monde au lieu d’un être-dans le monde27. La clôture est la condition de l’être pour le monde. La condition de clôture vaut pour l’ouverture infinie du fini : elle « représente finiment l’infinité ».

Elle donne au monde la possibilité de recommencer dans chaque monade. Il faut mettre le monde dans le sujet, afin que le sujet soit pour le monde. C’est cette torsion qui constitue le pli du monde et de l’âme. Et c’est elle qui donne à l’expression son trait fondamental : l’âme est l’expression du monde (actualité), mais parce que le monde est l’exprimé de l’âme (virtualité). Aussi Dieu ne crée-t-il les âmes expressives que parce qu’il crée le monde qu’elles expriment en l’incluant : de l’inflexion à l’inclusion. Enfin, pour que le virtuel s’incarne ou s’effectue, faut-il encore autre chose que cette actualisation dans l’âme ; ne faut-il pas aussi une réalisation dans la matière, si bien que les replis de cette matière viendraient redoubler les plis dans l’âme ? Nous ne pouvons pas le savoir encore, bien que le précédent chapitre invite à le croire.