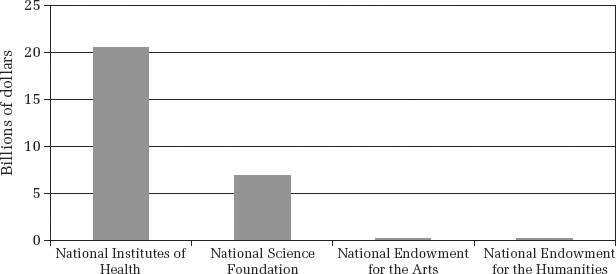
FIGURE 4.1: The U.S. federal government funds much more research in medicine and other scientific pursuits than research in the arts and humanities.
“A plowed field is no more part of nature than an asphalted street—and no less.”
—Herb Simon1
When President Obama extols science, saying, “Science is more essential for our prosperity, our health, our environment and our quality of life than it has ever been before,”2 he does not seek to persuade Americans of the importance of science. They already believe it. Surveys show that very high percentages of Americans (usually close to 90 percent) say that they are “very interested” in new scientific discoveries, and think that such discoveries have a positive impact on our quality of life. Furthermore, relatively few Americans see a downside to science. When prompted with possible negative effects—for example, that science “doesn’t pay enough attention to the moral values of society” or that science “makes our way of life change too fast”—a substantial minority of Americans agree, but the percentage is much lower than that observed in similar surveys in other countries. Americans see more advantages and fewer disadvantages to scientific advances than people from any other country for which comparable data are available (Brazil, China, European Union, India, Japan, Malaysia. Russia, South Korea).3
Americans also see it as natural and right that the federal government should pay for scientists to do their work. More than 80 percent agree with the simple statement “The government should fund basic research.” Indeed, 35 percent of Americans think that the federal government spends too little on science, and only 10 percent think that it spends too much (Figure 4.1).4 (The remainder think that the level of spending is about right, or have no opinion.)
FIGURE 4.1: The U.S. federal government funds much more research in medicine and other scientific pursuits than research in the arts and humanities.

The seeds of that public attitude and of enormous federal expenditures on scientific research may be found in World War II. The average citizen may not have been aware of the massive scientific efforts, organized by the U.S. Office of Scientific Research and Development, that went into developing radar, sonar, and advances in fuses, missile guidance systems, ordnance, aviation, and so on. But Americans were certainly aware of the role of science in the development of the atomic bomb. And they certainly were aware of the availability of penicillin. Although penicillin was identified as effective in treating bacterial infections in 1928, there was no way to produce it on a large scale. As late as June 1942, there was virtually no penicillin available to treat infections. Yet two years later, some two billion units of penicillin went with Allied soldiers to France on D-Day, the product of a new method of growing a new strain of penicillin (originally discovered on a moldy cantaloupe) in a liquid by-product of corn. Whether or not the atomic bomb ultimately saved Allied soldiers’ lives by averting the need to invade Japan is a matter of debate. That penicillin saved lives is not.
President Roosevelt knew exactly how important science had been to the war effort. In the autumn of 1944, when it began to look probable that the Allies would win the war in the next year or two, President Roosevelt asked Vannevar Bush, the head of the U.S. Office of Scientific Research and Development, to write a report outlining his vision of postwar scientific research. Many federal scientific projects responded to particular wartime needs that private sources simply could not address. Leaving the development of battle-worthy radar to private firms was not an option. But after the war, these needs would disappear. Should federal expenditures on science continue, or should they drop to near zero, the level before the war?
Bush argued that funding for science should continue, but with a different focus. The great majority of wartime monies had gone to “applied” research—that is, research meant to solve a specific problem. Bush’s report made a strong case for the importance of what he called “basic” research during peacetime.5
Bush described basic research as that “performed without thought of practical ends. It results in general knowledge and an understanding of nature and its laws.” Bush argued that basic research is actually the driving force behind successful applied research. Understanding the laws of nature could have far-ranging and unanticipated benefits. Bush went so far as to call scientific progress the “one essential key to our security as a nation, to our better health, to more jobs, to a higher standard of living, and to our cultural progress”—a formulation not far from that used by President Obama sixty-five years later.
Bush also reminded the president of the essential role that the federal government played in these scientific success stories, and he argued that the government ought to stay involved. Applied and basic research would inevitably compete for limited funding that private firms could allocate to research, and applied research would usually win. After all, applied research solves short-term problems and thus is likely to earn money. Bush argued (without much data to back him up) that basic research would ultimately pay for itself in improved productivity. (This argument would be supported by economic research in the 1950s.6)
Bush’s vision was that basic research tells us the secrets of nature. Applied research exploits that knowledge in the creation of new technologies. What, then, is education research, basic or applied? Education research is clearly applied—it is directed not at fundamental questions of nature but at solving a problem: How do we best educate children? We would imagine that the outcome of basic research, especially knowledge of how children think and learn, would be informative to education research. Great strides have been made in our knowledge of neuroscience—surely newfound knowledge of the mind and brain can help us improve schooling, right?
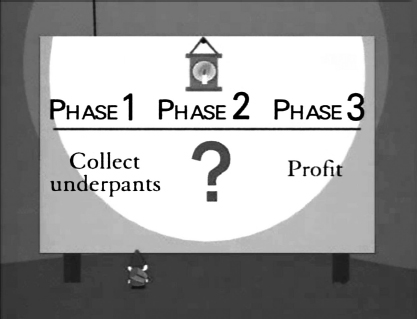
Surely newfound knowledge of the mind and brain can help us improve schooling. I’ve heard this phrase (or ones like it) countless times, and it increasingly reminds me of the Underpants Gnomes. In one episode of the animated television series South Park, a little boy swears that his underpants are stolen at night by gnomes. He and his friends stay up late and find that the Underpants Gnomes are real, and they follow them to their underpants processing facility. When pressed, the Gnomes explain their business plan, shown as a chart (Figure 4.2).
FIGURE 4.2: The business plan of the Underpants Gnomes.
Since the episode’s original broadcast in 1998, references to Underpants Gnomes have been used as a metaphor for poorly thought out business or political plans. In the case of education research, I think a similar plan is at work (Figure 4.3).
FIGURE 4.3: The relationship of basic and applied education research, modeled after the business plan of the Underpants Gnomes.
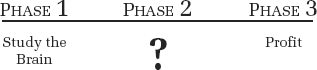
I realize that the Underpants Gnomes analogy may be a bit strained, but it highlights an important point. The need to flesh out phase 2 is obvious in the Underpants Gnomes’ business strategy. It is no less important in thinking about using basic research to improve education, although the need is less plain because it seems so obvious that learning more about how the mind and brain operate should improve education. In the remainder of this chapter, I will argue that such knowledge can help, but that the process is far from obvious.
To get a more detailed view of what phase 2 in Figure 4.3 might look like, we need to better understand the relationship between basic and applied research. We need to get beyond saying that “applied researchers can draw on basic research” to establishing a more systematic and general description of how that actually happens.
A useful starting point comes from the work of Herb Simon.7 Simon was a polymath, making profound and lasting contributions to several fields, including economics, organizational behavior, computer science, psychology, management theory, and political science.a Perhaps it was his position at the center of diverse fields that gave him such clarity about basic and applied research.
Simon’s description of the difference between them begins as Bush’s does, more or less. In basic research, the goal is the discovery of laws that describe natural phenomena. You take the world as it comes to you, and try to summarize it with general principles. Applied research, in contrast, is goal driven. You don’t want to describe the world as it is; you want to change the world to make it better. That’s the meaning behind the epigraph of this chapter: a plowed field is no more or less “natural” than an asphalted street because in each case, humans have altered the world to fulfill a purpose. Examples of applied sciences might include all the branches of engineering, architecture, urban planning, and education research.
Applied sciences typically call for the construction of an artifact—an object that serves the purpose of changing the world so that it’s more like what we want it to be. A civil engineer builds a bridge. An urban planner designs a park. And an educator writes a lesson plan.
Basic sciences can contribute to applied sciences by helping one understand how an artifact might work. For example, knowledge of physics and of materials science is useful to a civil engineer designing a bridge. She will use knowledge gleaned from these fields to predict whether the construction plan and materials she has in mind will yield a bridge that will stand or fall. Similarly, cognitive science might help an educator predict how the mind of a third-grader will respond to a lesson plan: will she find it comprehensible, will she remember it later, and so on. So far, so good, and kind of obvious.
But here’s a less obvious point to consider. I can use principles of physics to help me design a pendulum clock that will keep marvelous time in my living room, but that clock won’t work at all on board a ship. The ship’s rolling movements will render the pendulum movement useless. Similarly, a sundial won’t work in my living room. In determining whether an artifact is meeting the intended goal, we can’t attend only to the artifact. We must consider how the artifact interacts with the environment in which it is situated. Basic sciences may be useful here as well. We could use knowledge of physics to determine how much the movement of a ship affects the mechanism of the clock: Will a pendulum clock work despite the gentle rocking of a houseboat moored to a slip?
Now we’re in a better position to specify what happens during phase 2 of the Underpants Gnomes’ plan for education. Basic science can aid applied science by providing useful descriptions of the components of the artifact and the environment in which it’s situated. Simon called these the inner and outer environments. In the case of education, we expect that the inner environment would be the mind of the child, and information from cognitive psychology would be relevant—that is, as educators design lesson plans, they could draw inspiration from our knowledge of how the mind works. If the inner environment is the mind of the child, then the outer environment is the classroom; we ought to be concerned that, just as a clock works well or poorly depending on the environment, a particular lesson plan (or curriculum, or whatever) that might work for a child in one environment will not work at all in another environment. So basic science should be used to describe the environment—that is, the classroom.
This all sounds fairly straightforward, but we’ll spend most of this chapter elaborating on the difficulties that arise when one applies this method to education. Most of the time, these difficulties are ignored, and people try to get the benefit of the cloak of science on the cheap. Toward the end of the chapter I’ll describe a second, altogether different way that basic science can lend a hand to education. This method is subject to fewer problems, but it’s expensive. Likely for that reason, it’s rarely used.
What would you say about a mother who forbade television, video games, participation in school plays, sleepovers—even play dates? She does allow her child to participate in some activities—namely, homework and at least two hours of practice each day on a musical instrument. The goal? To ensure admission to Harvard University and to produce a math whiz or music prodigy. You may recognize this recipe for success as that of Amy Chua, also called the Tiger Mother. She published a piece in the Wall Street Journal describing her parenting style, under a title that seemed self-consciously provocative: “Why Chinese Mothers Are Superior.”8
And provoke it did. Chua took it for granted that the stereotypical academic success of Chinese students was true, and averred that the success was due to the tough-love parenting practices of Chinese mothers, who, she claimed, bully, criticize, spy on, and prod their children to great academic achievement.
Much outrage was directed at Chua, and virtually none of it questioned whether or not her methods “worked.” Few, if any, criticized her by saying “Bah, that’s no way to get your kid into Harvard!” Rather, they criticized her child-rearing goal: academic success, seemingly at any price. Chua claimed that she wants her kids to be happy too; she said kids become happy when they are good at something, but being good at something requires practice, and kids don’t want to practice, at first. But American readers—accurately, I think—felt that, when push came to shove, Chua was ready to choose that her child be good at something rather than be happy. Readers were not shocked by her methods because they thought they were ineffectual. They were shocked by her methods because they disapproved of her goals.
The French biologist Jean Rostand said, “Theories pass. The frog remains.” In other words, the frog—or, more generally, the natural world—is always present, available to let us know whether our theory (of frog physiology, or whatever it is) is any good. In basic sciences like biology, it’s clear to everyone whether or not the theory is any good, because we all agree on the yardstick by which it’s measured: agreement with nature.
That’s not so for applied sciences. The goal of an applied science is up for grabs. It is completely up to the individual as to what would make the world “better” and thus would be an appropriate target for applied scientific research. Does Amy Chua’s method of parenting “work”? If you share her goals, that’s an open question, and you could use methods of science to answer it. If you don’t share her goals for parenting, the question makes no sense.
In education research, the problem is still worse. It would be bad enough if we had a few different goals for educators to choose from, and there were an acrimonious debate about which was correct. Instead, the goal is underspecified or completely unstated. Thus we guarantee confusion and stagnation in research.
We invite confusion because how to use or respond to facts from basic science depends on one’s goal. Consider, for example, data from psychologists showing that people have many different mental abilities—that is, that there is not a single type of intelligence. This idea is best known to educators through Howard Gardner’s theory of multiple intelligences, although the idea has been strong in psychological theory since the 1930s; what has been controversial is the number of mental abilities and how to characterize them.9 Suppose that debate were settled, and there were reasonable agreement that there are, say, five types of intelligence: verbal, mathematical, spatial, musical, and emotional. (The last of these being the ability to understand the emotions of others and to understand and regulate one’s own emotions.). Let’s pretend that the evidence for this five-factor theory is very strong indeed, and insofar as we can know something scientifically, we know this fact. Some people are good with words, others with numbers; others are skilled musically; and so on. What would that mean for schooling?
What it means for schooling depends on your goals for schooling. Suppose I think that children attend school for self-actualization, a term from psychological theory that means to become all that you can become, to fulfill your potential. In this vision of education, schools should help children identify their strengths and develop them. With this goal in mind, the theory from psychology outlining the five types of intelligence is a godsend. My goal is to help each child discover his or her abilities—well, here’s a taxonomy of ability! When I see a child struggling verbally but excelling musically, I’ll have a way of thinking about why that’s so, and I’ll know that I should be sure to offer every musical opportunity to this child, while not pressing so hard on reading and writing.
But now suppose my goal for schooling is not self-actualization but preparation for the world of work. When today’s children someday seek a job and career, they will not compete only with the child down the street or across town; they will compete with children in Berlin, São Paulo, and Nanjing. We owe it to our kids and to their future prosperity to prepare them for this eventuality. With this goal in mind, the theory of intelligences is not just useless to me but possibly destructive. Most kids aren’t going to make a living by playing music, so I’m going to see music as an add-on, a fun extra that kids really ought to do on their own time. I don’t want a psychologist telling them that music is, in some sense, the equivalent of a practical ability like mathematics. The implications for education of a scientific fact depend on the goals of schooling.
Those goals, however, are usually undefined. Yes, schools have mission statements. So too do school districts and state departments of education. But let’s face it—they are typically not crisp, certain statements of purpose. Rather, they are dewy-eyed platitudes. If you find yourself in need of such a statement, I’ve got you covered (Figure 4.4).
FIGURE 4.4: Do-it-yourself school mission statement. Just move downward, choosing one or two phrases as directed.
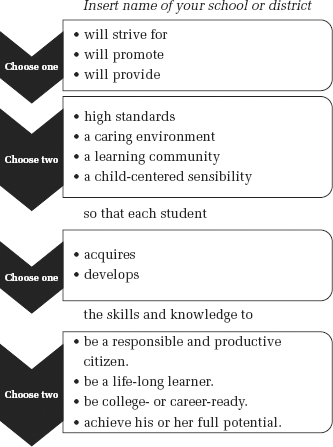
Such statements may serve other purposes, but they cannot help us when we’re trying to understand the implications of basic science for education. Science can affect education only if there is a clear statement of education goals.
Now, this problem shouldn’t be blown out of proportion. Even if the goals of schooling are not explicit, aren’t they kind of obvious? We want kids to know some science, some history, some math, and so on. That’s true enough, especially at the younger grades. But as kids get older, our long-term goals seem to loom larger. Do we want kids to learn American history so that they will be proud of their heritage or so that they will learn to thoughtfully question those in authority? If a kid doesn’t like math, is it okay for him to stop studying it once he knows enough to balance a checkbook and do his taxes? Or should every kid at least try to get through precalculus, so that we’re not shutting him off from future technical careers? How much emphasis should English classes place on aesthetic appreciation of literature versus more practical pursuits, such as expository writing? These are the kinds of questions that make school boards squirm because any answer will make someone angry. So people pretend that schools can be all things to all students, and the questions go unanswered. But the hidden cost to not answering the question “What are the goals of schooling?” is that education researchers can’t do their job.
A mayor can expect that constituents will feel justified in bringing the problems of the city to the mayor’s attention, even when the mayor is trying to enjoy a meal in a restaurant or shopping for groceries. New Yorkers are not known as the bashful sort, so we might expect that they would not be shy about approaching their mayor with unsolicited complaints or comments. That may be the reason that Ed Koch, New York’s mayor during the 1980s, would often beat them to the punch by asking for their opinions: a buoyant “How’m I doing?” became something of a catchphrase for Koch.
Some of this was political show, of course, but some part of it may have been a real desire for feedback. Sure, the mayor had access to opinion polls, but those might be written in a biased way, or the data might be “groomed” before Koch ever saw it. As General George Patton said, “No good decision was ever made in a swivel chair.” A good leader is hungry for reliable, on-the-ground feedback.
We often take feedback for granted, but it is essential for systems of all types: political, corporate, biological, and so on. In education, we can describe two functions of feedback. One is to provide information for ongoing correction. Even highly reliable systems have some error, and you need feedback about the error to correct it. For example, consider your ability to control your body. You probably have the general sense that you are highly accurate in making simple movements—reaching for a cup of coffee, stepping up on a curb, and so forth.
Try this. Pick a spot on your desk (or wherever you’re reading this book), close your eyes, and try to hit the spot with your finger. You’ll probably be pretty close, but you are unlikely to hit it directly. Now do the same thing again with your eyes open. If you are mindful of what you’re doing, you’ll notice that you make a pretty rapid movement that puts your fingertip in the ballpark of the target; then your hand slows down, and you move it the rest of the way to the target. During that moment that you slow down, you’re actually gathering feedback—you’re using vision to determine where your fingertip is relative to the target—so that you can compute the rest of the movement to put your finger exactly where you want it.10 Before you start the movement, your brain calculates what your muscles should do to move your hand to the target. That calculation is imperfect, however, even for a highly practiced skill like moving your hand. You need feedback along the way if you are to finish the movement exactly on target.
Analogous processes happen in the classroom. Just as your brain plans a sequence of muscle movements to get your hand to a target, a teacher plans a sequence of activities that will move the student’s mind toward a particular goal. The goal might be “knowledge of grammatical rules” or “a positive attitude about reading” or “an understanding of the consequences of bullying.” When you move your finger to a target, the corrective procedures you make midmovement are essential to reaching the target. The same is true of teaching and learning.
You need feedback in the middle of a complex action (a movement, or teaching) so that you can make corrections. You also need feedback at the end so that you can evaluate whether you’ve met your goal. If you have no feedback, how can you evaluate whether or not whatever you’re doing works? For example, many businesses have diversity awareness programs meant to teach their workers to respect variations in employee personality, age, ethnicity, and other dimensions. Yet only 36 percent of companies using such programs make any effort to evaluate whether the training has any impact!11
These points are fairly obvious for educational practice, but what do they have to do with education research? Feedback is necessary in education research in order for us to know whether or not the artifact is doing the intended job. If my goal for education is to improve creativity in kids or to make them more moral citizens, I need a way of measuring morality or creativity in order to know that my efforts are getting somewhere. As I write this, we have reasonably good tests in hand to measure content knowledge in most of the major subject matter areas. We don’t have good tests to measure students’ analytic abilities, creativity, enthusiasm, wisdom, or attitudes toward learning.
This caution is not to say, “If we can’t measure it, we shouldn’t try to teach it.” Our goals for schooling should be set by our values. The feedback problem is not about what should be taught—it’s about one limitation on science’s ability to help us reach our goals. This point is easily summarized: if someone approaches you with a curriculum that he claims will boost kids’ creativity, you might ask yourself how he knows whether or not it works.
A teacher recently told me a story about switching schools. He had long been a physical education instructor at a fairly traditional boys’ school, but when his wife’s firm transferred her, he ended up teaching at a somewhat larger, coed school with a very progressive sensibility. Students had much more latitude in selecting their work, and there was a lot of emphasis on collaboration and cooperation in all aspects of the school day. Given my description, you can imagine how things went on this teacher’s first day, when he tried to organize a soccer game of third-graders by naming captains and encouraging them to alternate picking teammates from among the remaining students. Some told him that they didn’t feel like playing soccer and wanted to do something else. Some protested his method of organizing teams. One little boy calmly told the teacher that he didn’t know what he was doing. “You’re new. You should ask us how we do things. That’s what we’re here for.”
This example illustrates the importance of the outer environment. A teaching method that had worked well in numerous classes for better than a decade imploded. Why? Because the sensibility of the class was different from any the teacher had encountered before. Students expected choice and collaboration in every lesson, features that had not been expected at his old school. His lesson plan was a pendulum clock placed on a ship. (He is a resourceful teacher, and it didn’t take him long to find his groove at the school.)
We need some description of the outer environment. We need to use basic science to characterize classrooms. For example, maybe the critical features of a classroom are the emotional warmth, the degree of organization, and the academic support offered.12 The problem, though, is that scientists know much more about children’s minds than they do about classrooms. There are serious, ongoing research programs addressing this issue, but the going has been slower.b
Let’s go back to the question raised by the Underpants Gnomes and the answer we’ve been working with. The question is “How can we use basic scientific knowledge to improve education?” and the answer is “Basic science provides a description of the inner environment and the outer environment.” I just finished saying that we shouldn’t expect too much by way of a description of the outer environment—the science just isn’t as far along on that problem. What about the inner environment? Do we know a lot about children’s minds? We do, but applying that knowledge is not as straightforward as you might imagine. Understanding why calls for some heavy lifting, but it’s probably the most important point in this chapter.
Let’s start this way. Take someone who knows a lot about children’s minds. She has considerable experience in tutoring individual kids, and she is terrific at it. Would we predict that this person will also be a great classroom teacher with, say, twenty-eight children? Our intuition says “not necessarily.” But why not? A classroom, after all, is composed of individual children, and if we propose that this teacher knows a great deal about individual children, why shouldn’t she be terrific in the classroom? Because kids interact, and those interactions pose challenges that the teacher never encountered when she taught individuals. Certainly, her prior experience and her skill will be of some benefit, but we can pretty much bet that there are aspects to handling a class that will be new to her.
The term levels of analysis describes this phenomenon: when you’ve analyzed something and understand it, your understanding applies only to what you’ve studied, not necessarily to a group of the things you’ve studied. We can generalize this principle. Just as knowing a lot about teaching an individual child does not mean that one will be equally successful in running a classroom, being a successful classroom teacher does not mean that one will necessarily be skilled in running a school, and a good school principal will not necessarily make a good district leader (Figure 4.5).
FIGURE 4.5: Some levels of analysis in education.

You can see in Figure 4.5 that I’ve defined the “child” level of analysis as an evaluation of whether or not the child has met some goal we set for schooling. “There’s DeAndre. Can he multiply two-digit numbers consistently?” Or “There’s John. Does he know his colors?” When we evaluate “the child,” we’re saying, “I want kids to be able to do X . . . can this child do it?”
Well, what about levels below—that is, more fine grained than that of “the child”? That’s the province of educational psychologists and cognitive psychologists. We want to know the mental processes that underlie abilities like “reading success” or “proficiency in mathematics” (Figure 4.6).
FIGURE 4.6: Hypothetical mental contributors to proficiency in mathematics.
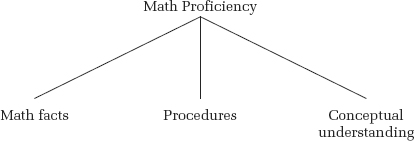
Okay, what mental abilities does a child need to be proficient in mathematics? I may propose that three abilities must be in place: the child must have memorized a small number of math facts (like 2 + 2 = 4); the child must know relevant math procedures (that is, algorithms, ways of solving standard problems); and the child must have a conceptual understanding of why and how those algorithms work. Each is a hypothetical entity I use to build a theory of a child’s overall math competence.
But then someone might ask me, “What about these procedures? What does it take for a child to know how to use procedures?” In response to that question, I might try to come up with a theory of the mental processes underlying mathematical procedures. “Well, the child needs some background knowledge—that is, she has to memorize the procedures; and she needs working memory capacity—that’s the mental space in which she’s going to manipulate numbers with these procedures; and then she needs processing speed, which is sort of like the mental fuel to get this work done.” (Figure 4.7).
FIGURE 4.7: Hypothetical mental contributors to the use of mathematical procedures.
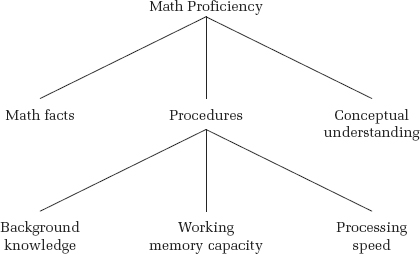
As you’d guess, people ask, “How does working memory work?” and we get even more detailed. If this deconstruction of mathematical proficiency isn’t very clear to you, don’t worry about it. Here’s the main point. As we pick these mental processes apart, we’re creating new levels of analysis—I’ll call them educational processes and cognitive processes (Figure 4.8).
FIGURE 4.8: More levels of analysis in education research.

It is clear that what we know at one level of analysis doesn’t necessarily translate up perfectly—my knowledge of how to tutor kids individually might help me as a classroom teacher of twenty-eight, but it sure doesn’t guarantee that I know all I need to know. The same thing applies at these other levels of analysis. Knowing something about how kids acquire math facts might help me improve students’ overall math proficiency, but we actually have the same problem we had in going from one kid to a classroom. Kids interact, so a classroom has features that individual kids don’t have. In the same way, I might understand something about math facts, but math facts interact with other mental processes to produce math proficiency. So what I know about math facts may not apply perfectly well once it’s in the context of all those other contributing processes.c
The semi-independence of these levels is wonderful for researchers because it reassures them that it makes sense to study just one level. For example, suppose a researcher said, “I study reading.” I might reply, “That’s dumb. You know that reading must be composed of other, more basic processes like attention, vision, and memory. Why don’t you study attention, vision, and memory? Once you’ve got those figured out, you’ll understand reading!” Then another researcher might say, “No, Willingham, you’re dumb. We know that the mind is a product of the brain. What we ought to do is study the brain!”
The semi-independence of these levels means that each ought to be studied on its own. Knowing a lot about cognitive processes is not a guarantee that I’m going to understand reading, for just the same reason that knowing how to teach one child is not a guarantee that I’ll be able to run a classroom. If you want to understand reading, you have to study reading.
As I said, that’s wonderful for researchers, but there’s a less-wonderful implication for the application of basic scientific knowledge to classrooms. Information from lower levels is not guaranteed to apply to higher levels in a straightforward way, and all the information from basic sciences that we hoped to apply to education is at the lower levels. The lowest level in Figure 4.8 that educators might care about is the child—educators want children to learn. Changing things at lower levels is not enough. For example, suppose you and I had this conversation:
ME: I figured out how to increase a child’s working memory capacity!
YOU: Cool! Can she read with better understanding? Is her understanding of fractions richer? Does she like learning more?
ME: Uh. . . I don’t know.
YOU: (pause) Oh.
Here’s an example of how the application of cognitive principles can sound good, but fail. The spiral curriculum was introduced in the early 1960s by cognitive psychologist Jerome Bruner.13 The idea is that students revisit the same fundamental concepts across several years, each time with greater depth. To a cognitive psychologist, this sounds great. It means that a lot of time elapses between when kids study the same basic idea, which is very good for memory. It means that students will hear the same important ideas from different teachers, so if a student doesn’t quite understand the way one teacher explains it, there will be another opportunity the following year. So again, in terms of two processes at a cognitive level of analysis—memory and comprehension—the spiral curriculum sounds like a win.
But once it was implemented in classrooms, it became clear that a spiral curriculum was subject to at least two serious drawbacks. First, students don’t stick with any topic long enough to develop a deep conceptual understanding of it. Countries that seem to do a better job teaching math, for example, have curricula in which a small number of topics are studied intensively during the year and then are not revisited.14 Another drawback of the spiral curriculum was pointed out to me (indirectly) by my oldest daughter. When she revisited a topic in the fifth grade that she had studied in the fourth grade, her reaction was “Not this again!” Never mind that she had not understood it all that well the previous year. As far as she was concerned, “We did this already.” Lots of time between practice is great for memory, but it turns out to have unexpected implications for motivation.
Does the levels-of-analysis problem mean that educational psychology is useless? Not at all. There are three ways that basic scientific information from lower levels of analysis can benefit education. First, if we have a detailed theory of how the levels relate to one another, then we can successfully predict what happens when we go from one level to another and so avoid the problem I’ve described. I’ll know how the different pieces interact, so I can predict, “Yup, practicing math facts will help long division, and here’s why . . .”
Second, we can use data from educational (or cognitive) psychology when we think that the effect we’re looking at is so large and so robust that we are pretty confident that it will translate to higher levels in nearly all situations, even if we don’t have a detailed theory of how that translation happens. For example, practice is so important to learning that I might predict that it’s always going to be important; it doesn’t matter whether you are learning to improvise in jazz or learning to garden or learning to integrate in calculus—practice is necessary to improve, and there aren’t going to be strange interactions at other levels that make that need go away. This of course doesn’t mean that the principle can be applied mindlessly. Another universal fact about cognition is that enforced, repetitive practice is detrimental to motivation.
The third and final way that you can use data from basic science is to evaluate a claim made by the purveyor of an education product. If someone promotes a curriculum or teaching method by claiming that it capitalizes on a feature of the mind, cognitive or educational psychology might have information as to whether the feature of the mind is accurately described. For example, the Core Knowledge Foundation offers a curricular sequence that emphasizes content knowledge15 and argues that this emphasis is useful because reading comprehension depends on content knowledge. That’s a claim about how reading works, independent of any claim about whether or not the core knowledge sequence helps kids learn to read better. In this case, the claim about the mind is correct.16
In other cases, the claim is clearly false. For example, type “left brain right brain education” into an Internet search engine, and you will find a great many education products that claim to be based on the scientifically established differences between the right and left hemispheres of the brain. In virtually every case, the characterization of the differences is wildly exaggerated. There are differences in what the two hemispheres of the brain do, but for most tasks, most of the brain is involved, and it doesn’t make sense to talk about the left brain as “linguistic and logical” and the right brain as “emotional and artistic.”17
We’ve reviewed four challenges to applying data from natural science to education when using the first method of applying basic science to problems. Let’s review them:
These four problems must always be solved when we seek to apply basic scientific knowledge in education research. For some topics—for example, learning to read—the problems are largely solved, and there are real opportunities to use basic science in education. For others—for example, teaching students to think critically—the answers are less clear. Feedback is a particular problem in critical thinking research, because critical thinking is so difficult to measure. As we’ll see in future chapters, clarity about whether these problems are solved can help you evaluate claims that an educational program is “research based.”
This first method—drawing on principles of basic science—is, unfortunately, very easy to do sloppily. You can take a finding that sounds somewhat peripherally related to whatever educational panacea you’re peddling, wave it around, and say “Look: research!” It’s cheap, because the research already exists. But as you’ve seen in this section, it’s pretty difficult to do it well.
Thus far we’ve discussed one way of applying basic scientific knowledge to education: characterizing the inner and the outer environment. But there is a second method. This method is easier to do well, because there are fewer problems to be solved. But it’s very expensive because there will not be existing research waiting for you to use. The researcher will be starting from scratch.
Recall the Science Cycle from Chapter Three (illustrated again here as Figure 4.9).
FIGURE 4.9: The Science Cycle.
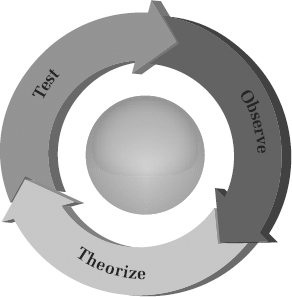
The stage in the cycle marked “Test” refers to the testing of a prediction. When we create an artifact in an applied science, we want to test whether the artifact is doing what we expect—that is, whether it is meeting the goal that we’ve set. Even when the knowledge that we’re applying from the basic sciences is very sound, we can’t necessarily be certain that the artifacts we create will behave as expected.
For example, consider the problems architects face when they plan a large building, such as the Epic tower in Miami, a forty-eight-story residential building. In the case of the Epic, architects needed to be sure that the building could withstand wind forces that one would expect at its location on Biscayne Bay. Basic science can provide wonderfully accurate information about the outer environment: the wind forces and other weather elements to which the Epic would be exposed, and the way that those forces differ at ground level compared to an altitude of five hundred feet, the height of the building. Basic science could also provide excellent information about the inner environment: the tensile, compressive, and shear strength of the materials used, for example. You might think, therefore, that the architects could calculate with great confidence how their design would stand up to wind forces. But they (like all builders of skyscrapers) were not satisfied with the predictions derived from this basic scientific information, accurate though it might be. They constructed a highly detailed scale model of the building and put it in a wind tunnel, to be sure that it reacted as predicted (Figure 4.10).
FIGURE 4.10: At top, a wind tunnel containing a scale model of the Epic skyscraper, surrounded by models of neighboring buildings. At bottom, the model of the Epic skyscraper showing sensors that would detect movement of the model in the wind tunnel.

In education, we create a series of lesson plans for algebra, for example, in the expectation that kids who experience those lesson plans will meet some criterion for knowledge that we have set. But how do we know whether this new set of lesson plans is more effective than whatever we were doing to teach algebra before? Don’t we need to compare the new method to the old method? Making such comparisons is the bread-and-butter of basic science. It’s the Test phase of the Science Cycle. So the second way that basic science can be used in an applied pursuit like education is to take advantage of methods developed in the basic sciences to evaluate whether our applied methods are effective.
An interesting feature of this second method is that the inspiration for the method you’re testing could come from anywhere. In the first method, we were talking about using basic science to derive a method of teaching, say, chemistry. But now we’re talking about using techniques from science to compare two methods of teaching chemistry, and those two teaching methods could come from anywhere: my experience, another teacher’s experience, or thin air.
In applied sciences, you can often create the artifact without basic scientific knowledge. For example, people have been building bridges for thousands of years, and for most of that time, builders were not guided by scientific knowledge of physics. The Ponte Fabricio was built around 62 BC, centuries before classical physics was well formulated—yet it still stands and is still in use (Figure 4.11).
FIGURE 4.11: The Ponte Fabricio in Rome. This bridge is functional, beautiful, and enduring, and it was built long before classical physical principles were worked out.

Even when we do not have basic scientific knowledge guiding the building of the artifact, we can still use the scientific method to evaluate the artifact. Bridge builders of old would have done so implicitly: keep using the designs that lead to strong, enduring bridges; discard the designs of the bridges that collapse. Craft knowledge comes from this sort of experience. The scientific method just makes such comparisons more reliable by making them more systematic, as we discussed in Chapter Three.
Thus, even though basic scientific knowledge may provide very little solid information for how to design a curriculum that will improve civic engagement, we can still use the scientific method to compare two existing curricula to see which one does a better job of promoting civic engagement. Compared with the first method, this method poses fewer challenges. We still need to define the goal, and we still need some reliable feedback measure. That is, we need to decide what we mean by “civic engagement” and how to measure it. But we needn’t worry about the other two problems—characterizing the inner and outer environments, and that complex interactions lead to surprising outcomes.
Happily, the two problems that stick with us using this method can be solved provisionally. In other words, I could say, “All right, I know this definition isn’t perfect, but let’s say that ‘civic engagement’ means participating in civic institutions. And I’ll measure it by asking high school seniors whether they do volunteer work at such an institution, whether they follow news stories about these institutions in local media, and whether they say that they have an interest in these matters.” I can then use scientific methods to compare two curricula for their success in promoting civic engagement.
The danger in this strategy—and it is significant—is that if my definition or measure of civic engagement is dopey, I can easily kid myself into thinking that I have successfully compared the two curricula when in fact my comparison was flawed from the start because I used a dopey definition or a dopey measure. But you’ve got to start somewhere, and it seems to make sense to measure things as best you can and to try to improve the measures as you go, rather than to throw up your hands in despair.
In sum, the second method is more straightforward than the first. If I scientifically compare two curricula or two teaching strategies, or parochial schools versus public schools, I do need to worry about what’s being measured and how. But if the measurement seems pretty straightforward—for example, a reading test for third-graders, of which there are several good ones—we can conduct a good study. Sure, there are lots of ways to mess up a research project, but we’re at least playing to the strengths of the scientific method, meaning that the ways to mess up the study are understood, and there are strategies for dealing with them.
In the first method I described, the payoff can be much greater, but the likelihood that you’ll actually see some payoff is much lower. The second method simply compares two bridges and tells you which does a better job. At the end of the day, you’re likely to know which of those two bridges is better, but you’re left without any information as to how to build an even better bridge. The promise of the first method is that you’ll be able to use scientific principles to inspire a better bridge than anyone has yet imagined, because you understand in the abstract what makes a bridge long lasting and strong. But as we described in this chapter, deriving practical artifacts from those abstract principles is not straightforward.
So for all the talk about brain science leading to a revolution in education, that road seems much more difficult than the process of comparing existing curricula and teaching methods. Perhaps the old adage has it right: one good thief is worth ten scholars. In other words, the smart thing to do is to find the best existing curriculum and copy it. Then perhaps tweak it here and there, and use the scientific method to see whether your tweaked version has made it still better. Perhaps. But I think that this vision is too pessimistic about the contribution that basic science might make to education research. I do think that progress in our understanding of learning, reading, and mathematics—the three topics most heavily studied—have already paid dividends. Just how much help basic science has provided to education is, of course, a matter of opinion, and justifying my opinion would take us too far afield.
We’ve examined in some detail what scientists call “good science” (Chapter Three) and the challenges and opportunities in using good science to improve education (Chapter Four). Armed with this knowledge, we can begin to examine ways of evaluating scientific claims about education that you encounter.
a He was awarded the Turing Award by the Association for Computing Machinery (often called the “Nobel Prize for computer science”) for his contributions to artificial intelligence. He was awarded the American Psychological Association’s Award for Outstanding Lifetime Achievement Contributions to Psychology for his work in human decision making and problem solving. And he won the Nobel Prize in economics for his contributions to microeconomic theory.
b The logistics of doing research on classrooms is more difficult. Why? (1) To study a child, you need parental permission. To study a classroom, you need permission from school officials, who are understandably reluctant to grant it. After all, the mission of the school is to educate, not to conduct research, and what if the study interferes with education? (2) If I gain access to a school, I might be able to observe, say, twenty classrooms. But that school also contains, say, 450 kids. It’s easier to complete a study of kids because there are more of them.
c This distance problem is also a significant challenge for people trying to apply neuroscientific knowledge to education. There is a lot of excitement about “brain-based education” right now, but getting from the basic scientific data to something usable in the classroom is not easy. You need to translate not only the cognitive scientific data into educational practice but also the neuroscientific data into cognitive data. For more on this problem and how to solve it, see Willingham, D. T., & Lloyd, J. W. (2007). How educational theories can use neuroscientific data. Mind, Brain, and Education, 1, 140–149.
Notes
1. Simon, H. A. (1996). The sciences of the artificial (3rd ed.). Cambridge, MA: MIT Press, p. 3.
2. Remarks by the president at the annual meeting of the National Academy of Sciences. (2009, April 27). Available online at http://www.whitehouse.gov/the-press-office/remarks-president-national-academy-sciences-annual-meeting.
3. National Science Board. (2010). Science and technology: Public attitudes and understanding. In Science and engineering indicators 2010 (NSB 10-01). Arlington, VA: National Science Foundation. Available online at http://www.nsf.gov/statistics/seind10/c7/c7h.htm.
4. Ibid.
5. Bush, V. (1945, July 25). Science: The endless frontier. Washington, DC: U.S. Government Printing Office. Available online at http://www.nsf.gov/od/lpa/nsf50/vbush1945.htm. Roosevelt died before the report was completed. It was delivered to President Truman.
6. Solow, R. M. (1957). Technical change and the aggregate production function. Review of Economics and Statistics, 39, 312–320. For a more recent review, see Committee on Prospering in the Global Economy of the 21st Century. (2007). Rising above the gathering storm: Energizing and employing America for a brighter economic future. Washington, DC: National Academies Press. Available online at http://www.nap.edu/catalog.php?record_id=11463. There is also evidence that when the student population of a country is well trained in science, there is a substantial economic benefit; scientific knowledge makes for a high-quality labor force. See Hanushek, E. A., & Woessmann, L. (2010). The high cost of low educational performance: The long-run impact of improving PISA outcomes. Paris: OECD.
7. My discussion is based on Simon, 1996. Simon in fact uses the terms “Natural science” and “Artificial science,” rather than basic and applied research, respectively. For the sake of clarity, I’ll continue to use the latter set of terms.
8. Chua, A. (2011, January 8). Why Chinese mothers are superior. Wall Street Journal. Available online at http://online.wsj.com/article/SB10001424052748704111504576059713528698754.html.
9. Gardner, H. E. (1983). Frames of mind. New York: Basic Books. Prominent psychological theories arguing for multiple types of ability have been proposed by Louis Thurstone (1930s–1940s), Cyril Burt (1930s–1940s), Raymond Cattell (1940s–1950s), Joy Paul Guilford (1950s–1960s), and John Carroll (1990s). I discuss the differences between Gardner’s theory and these others in my book Why Don’t Students Like School?
10. The exact mechanisms by which even simple pointing movements are computed is a matter of some debate. See, for example, Meyer, D. E., Smith, J. E., & Wright, C. E. (1982). Models for the speed and accuracy of aimed movements. Psychological Review, 89, 449–482.
11. Society for Human Resource Management. (2010). Workplace diversity practices: How has diversity and inclusion changed over time? Available online at http://www.shrm.org/Research/SurveyFindings/Articles/Pages/WorkplaceDiversityPractices.aspx.
12. Those features have, indeed, been proposed as one characterization of an effective classroom. Pianta, R. C., La Paro, K. M., & Hamre, B. K. (2008). Classroom assessment scoring system. Baltimore: Brooks.
13. Bruner, J. (1960). The process of education. Cambridge, MA: Harvard University Press.
14. Schmidt, W., Wang, H. C., & McKnight, C. C. (2005). Curriculum coherence: An examination of U.S. mathematics and science content standards from an international perspective. Journal of Curriculum Studies, 37, 525–559.
15. Core Knowledge Foundation. (2010). The core knowledge sequence: Content and skill guidelines for kindergarten–grade 8. Charlottesville, VA: Core Knowledge Foundation. Available online at http://www.coreknowledge.org/mimik/mimik_uploads/documents/480/CKFSequence_Rev.pdf.
16. For example, Van Dijk, T., & Kintsch, W. (1983). Strategies of discourse comprehension. New York: Academic Press.
17. For more on this, see Willingham, D. T. (2010, September 20). Left-right brain theory is bunk. Available online at http://voices.washingtonpost.com/answer-sheet/daniel-willingham/willingham-the-leftright-brain.html. See also this chapter by Mike Gazzaniga (one of the pioneers of this area of research) written twenty-five years ago in which he tries to calm down the hype: Gazzaniga, M. S. (1985). Left-brain, right-brain mania: A debunking. In The social brain (pp. 47–59). New York: Basic Books.