OK, that sounds great – but can you explain a bit more about how convolution actually works?
Sure, and let’s keep this simple. As touched on earlier, convolution is a common image processing technique that changes the intensities of a pixel to reflect the intensities of the surrounding pixels. A common use of convolution is to create image filters. Using convolution, you can get popular image effects like blur, sharpen, and edge detection. Below, a well-known image that has been widely used in image processing is used to illustrate the effects of a slight blur. This image has in fact been employed since 1973 in the machine vision community, to illustrate image processing. Quite recently I was chatting with a researcher who told me they had just attended a conference where this image was shown, and they didn’t like it – they thought it was sexist and they were considering complaining about it. Good Grief!
An example of image processing; softening or blurring. (Standard test image that has been widely employed in the field of image processing since 1973.)
To achieve effects such as the one shown above, convolution is performed using a grid-like mathematical construct called a kernel
. The figure below represents a 3 x 3 kernel. The height and width of
the kernel do not have to be the same, though they must both be odd numbers. The numbers inside the kernel dictate the overall effect of the convolution. The kernel (or more specifically, the values held within the kernel) is what determines how to transform the pixels from the original image into the pixels of the processed image.
A kernel for use in convolution. (Illustration by the author.)
Convolutions are ‘per-pixel operations’ - the same arithmetic is repeated for every pixel in the image. Bigger images, therefore, require more convolution arithmetic than the same operation on a smaller image. The numbers in the kernel represent the amount by which to multiply the number underneath it. The number underneath represents the intensity of the pixel over which the kernel element is hovering. The process multiplies each number in the kernel by the pixel intensity value directly underneath it. This should result in as many products as there are numbers in the kernel (per pixel). The figure below shows how a kernel with 9 pixels operates on one pixel.
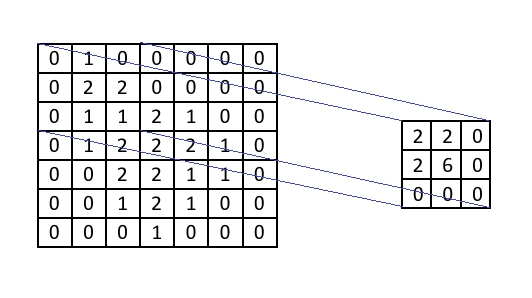
How image convolution works. The centre element the kernel is placed over is called the source pixel. The source pixel is replaced by the sum of the multiplied (weighted) values of itself and
nearby pixels. In this case the source pixel originally has a value of 2, and this would be replaced by (0+1x2+0+0+2x6+0+0+0+0) = 14. (Illustration by the author.)
The final step of the process sums all the products together and this value becomes the new intensity of the pixel that was directly under the centre of the kernel. The blur effect shown on the last page for the image of the lady, can be produced by a filter that is known as the ‘mean filter’. Here, all the values in the kernel are 1 and the sum of the products is divided by the amount of numbers in the kernel. The result is to soften or blur the image (with the extent of the blurring depending upon the size of the kernel used), as well as providing an additional benefit of removing any pixel (or ‘speckle’) noise in the image. The latter was made use of for the first images sent back from the Apollo voyages to the Moon – to reduce the noise in the images received on Earth as Neil Armstrong made his ‘giant leap’ for mankind by stepping down from the Lunar Module onto the surface of the Moon.
Now, I hope that is all clear and that you are now wised-up about convolution. That bloody well better be the case, since I can’t go through it again
.


