Fine and dandy, but can you give a simple explanation for how CNNs make use of convolution for identifying objects?

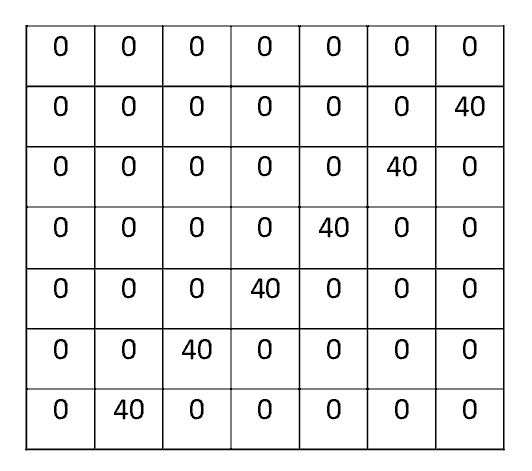
No problemo. We will consider a simple example of how convolution helps with automatic feature identification. Let’s say our first kernel (or filter) is 7 x 7 and is going to be a diagonal line detector. As a line detector, the filter will have a pixel structure in which there will be higher numerical values along the area that is in the shape of a diagonal line. This is shown below; and due to the fact that our lives in our house seem to be pretty much dominated by cats (with think we are the masters, but I can see from the expressions on their faces that they know better…), I have taken the liberty of using an image of a cat in this example.

A simple line detector filter (left) and corresponding diagonal line feature (right). (Illustrations by the author.)

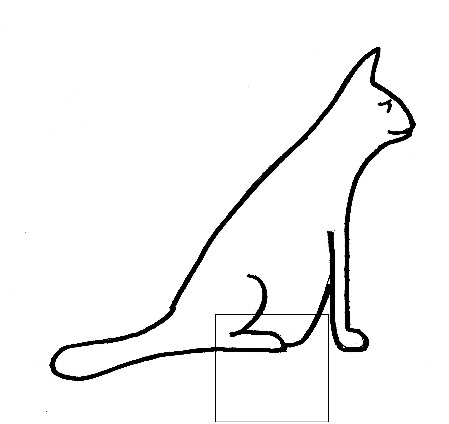
When we employ this filter on a given region of the input image, we compute multiplications between the filter and pixel values at that region. Now let’s take an example of an image that we want to classify, and let’s put our filter at the top of the cat’s back.

Applying the line detector to an image of a cat; original image is on the left and visualisation of the filter on the image (near the top of the cat’s back), is on the right. (Illustrations by the author.)

We multiply the values in the filter with the original pixel values of the image. If, in the input image, there is a shape that generally resembles the diagonal line that this filter is representing, then all of the multiplications summed together will result in a large value:

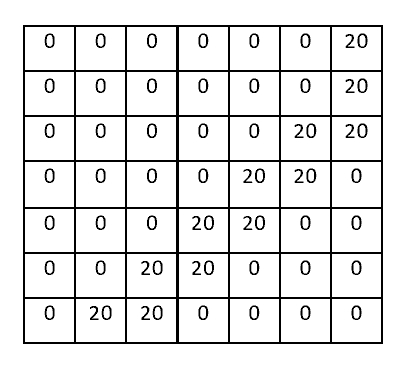
Visualisation of the receptive field on the cat (left), pixel representation of the receptive field (centre) and pixel representation of the filter (right). Convolution with our line detector filter on the back of the cat produces a large number: (20x40)+(20x40)+(20*40)+(20*40)+(20*40)+(20*40) = 4,800. (Illustrations by the author.)

Now let’s see what happens when we move our filter:

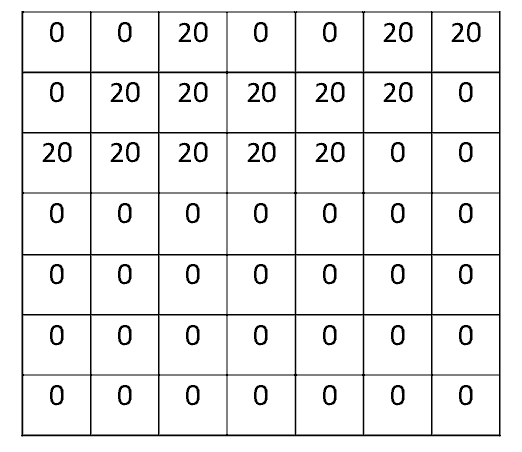
Again, the visualisation of the receptive field on the cat is on the left, with pixel representation of the receptive field centre and the pixel representation of the filter on the right. This time, the multiplication and summation does not give a large number, in fact convolution with our line detector filter on the lower part of the cat produces zero!

The value is much lower – in fact, it’s zero. This is because there wasn’t anything in the image section that responded to the line detector filter. Remember, the output of the image convolution is an activation map (or feature map). So, in the simple case of a one filter convolution (and if that filter is a line detector), the activation map will show the areas in which there are most likely to be lines in the picture. This is just for one filter; a simple filter that is going to detect lines that go from the bottom left to the top right. We can have other filters for lines in other directions and for various curves. The more filters, the greater the depth of the activation map, and the more information we have about the input. The above filter is a simplistic one to show how the convolution works – in real CNN applications they are more complicated. To summarise, the filters convolve around the input image and “activate” (or compute high values) when the specific feature it is looking for is in the input image.

Therefore, the convolutional layer is the core building block of a CNN. The layer's parameters consist of a set of learnable filters (or kernels). Each feature map shows the detection of some specific type of feature at some spatial position in the input. Using various filters creates a series of activation maps and these are stacked up to form what is known as the full output volume of the convolution layer.

To give you just a bit more information on how CNNs work, the hidden layers of a CNN typically consist of the convolutional layers we have just been discussing, as well as a RELU layer (to remove negative values and help with training), pooling layers, and fully connected layers. Pooling layers reduce the dimensions of the data by combining the outputs of neuron clusters at one layer into a single neuron in the next layer. Fully connected layers connect every neuron in one layer to every neuron in another layer – as in a traditional multi-layer neural network. The fully connected layers classify the images. I admit that this can all sound a little complicated when first explained, but the point is that you don’t necessarily need to know about all the intricacies of CNN architectures in order to make good use of them. And as you use them, you inevitably learn more about their composition and modes of operation. It is true that in order to model very complex data you need complex models, but the great beauty of CNNs is that, once you know how to train them for given sets of data, the network itself generates the complex model automatically – without you having to fashion its complexity manually – as we used to have to do years ago, using formal mathematical modelling, statistics, or whatever tools were available to us. And as well as being laborious, the old methods were generally limited to modelling relatively simple or structured situations.

So, here’s a summary of the situation regarding CNNs: convolutional neural networks automatically identify characteristics of a dataset that can be used as reliable indicators i.e. features. Historically, the conventional approach was for researchers to put vast efforts into ‘hand-crafting’ exhaustive sets of features for image classification. Since the advent of deep learning/CNNs, the conventional approach has been exceeded in accuracy for almost every data type. Impressive, eh? Grazie padrini !