Implications of special relativity for very high-speed travel

“When you are courting a nice girl, an hour seems like a second. When you sit on a red-hot cinder a second seems like an hour. That's relativity.”

― Albert Einstein

In 1905, Einstein published his famous paper that described his special theory of relativity (SR). SR comprises two postulates that are particularly relevant to very high-speed/interstellar travel:

1. The laws of physics are identical in all inertial systems (i.e., non-accelerating frames of reference); and all velocities are measured relative to a specified frame of reference – hence the term ‘Relativity’.

2. The speed of light (and other electromagnetic radiation) in a vacuum, is always constant at 300 million metres per second.

These postulates were something of a revolution in physics at the time, since from the 16th until the late 19th century it was generally believed that the Universe had an ‘absolute’ coordinate frame, which could ultimately be used to measure the absolute position and velocity of all objects. There was a theory of a somewhat elusive/ethereal ‘material’ known as the ‘aether’, through which light was thought to travel. It was believed that the aether provided the coordinate frame that could be used to specify the absolute position and velocity of all objects in the Universe. And I, for one, am not surprised that they came up with this theory. To start with, it seems completely reasonable that a wave should need some kind of medium to travel through. Waves that mankind has been aware of over the ages certainly do travel through media – sound through air, waves on the sea through water, and so on. Also, light always seems to be measured as travelling at a constant speed – which again, would be analogous to the constant speed of sound in air. Despite all this, the theory of the aether was dealt a significant blow in 1887, when Michelson and Morley undertook and published a famous experiment. It had been assumed that if the aether existed, then movement of the Sun in the Milky Way Galaxy and also the rotation of the Earth around the Sun would constitute movements through the aether; so that if light travel were measured in two perpendicular directions, the speeds would be found to be different. But in the Michelson-Morley experiment, the measured speeds in the two directions were found to be similar – and, as we know, data are king.

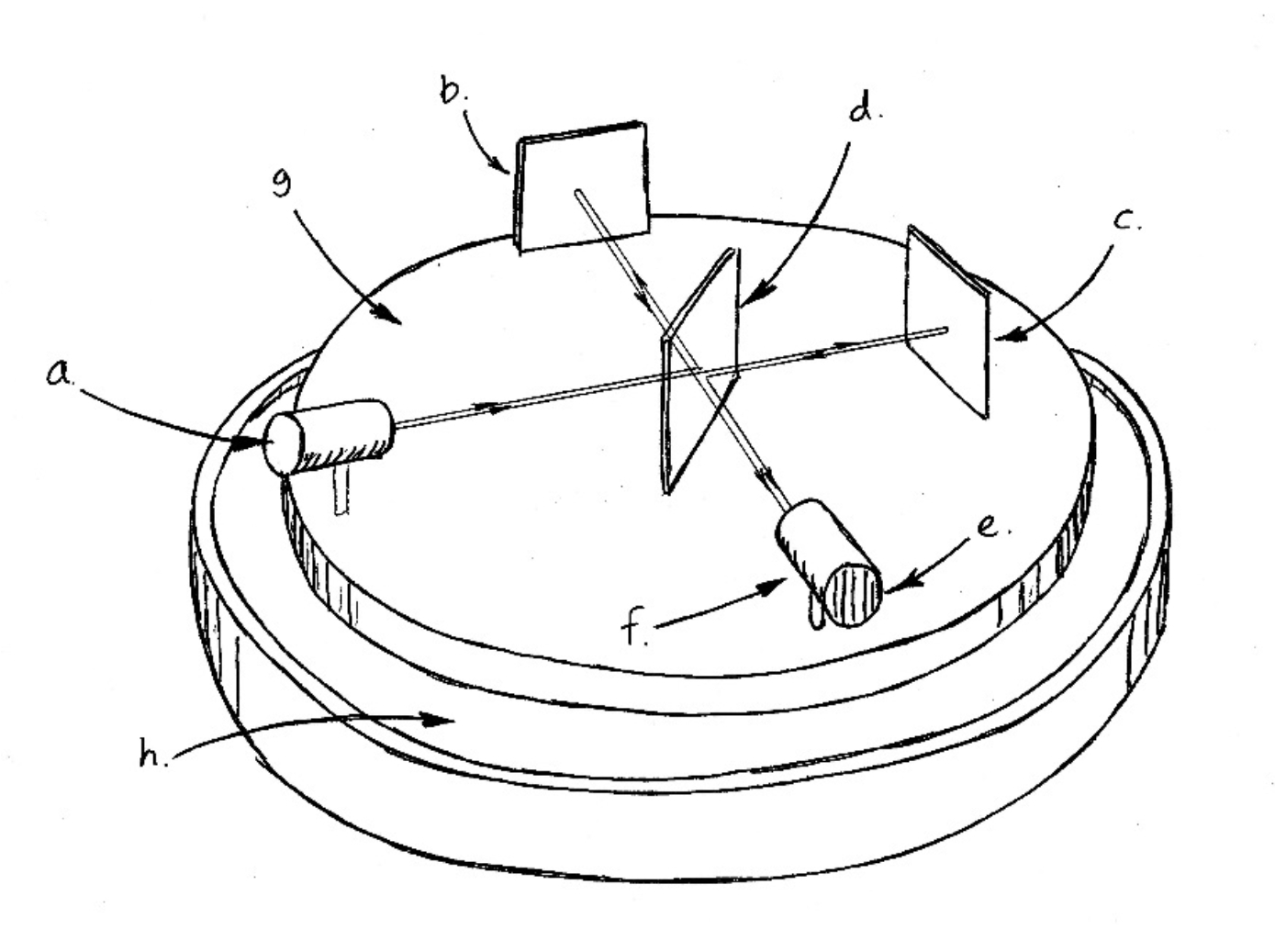
The Michelson-Morley experiment: (a) light source, (b) and (c) mirrors, (d) half-silvered mirror, (e) interference fringes, (f) telescope, (g) granite block and (h) pool of mercury. (Pen and ink drawing by the author.)

To cut a long story short, this provides strong support for postulate 2 of SR, that the speed of light in a given medium is always constant, and indicates that the aether, as it had been understood up to that time, does not exist. Since the Michelson-Morley experiment, there has been a good deal of further experimentation that supports the experiment’s findings and confirms that postulates 1 and 2 are correct to a high level of accuracy. Acceptance of this implies that time dilation will be observed.

It should be noted that there are two types of time dilation – one associated with special relativity (SRTD) and the other associated with general relativity (GRTD), with the latter addressing the effects of gravity (as mentioned above) and acceleration. SRTD is a difference in the elapsed time observed by two travellers due to a velocity relative to each other. Here, the word ‘observed’ is important since the time dilation is only observed because one traveller is moving relative to the other while using the fastest known phenomenon, i.e. light, to make the observations. The word ‘relative’ is also important since the amount of time dilation observed only depends upon the velocity of one traveller relative to the other. But is SRTD real ? We know that GRTD is real – if two travellers synchronised their watches, then one went close to a very massive object for a while, and then came back to meet the other and compared watches, they would find that the watch of the one who had gone near to the object would be reading an earlier time – time would, literally, have slowed down for him/her (as per Interstellar ). But would this be true of the two moving travellers mentioned above? If they slowed down, turned around, came back together and compared their watches, would one read differently from the other? If so, which would read the earlier time and why? If they read the same time, SRTD would not be real, and instead would only be an apparent, rather than a real, objective effect.

The above discussion is important in relation to determining if it may be possible for humans to travel at faster than light speeds. Over the years, many statements have been made in various publications that assert the impossibility of humans ever travelling at speeds greater than that of light. One of the most recent was a BBC Earth article entitled: ‘This video explains why we cannot go faster than light’. The authors of this piece had the temerity to accompany the text with a video depicting the starship Enterprise from Star Trek ! (This is, of course, anathema to your average trekker, who, like Star Trek itself, wishes to believe in a positive view of the future where all manner of scientific feats are accomplished, no matter how difficult or unlikely they may currently seem to be. Not to mention the slight on the great hero character which the Enterprise herself comprises.) The arguments put forward in this article and others, as explanations for c being a ‘speed limit’ could, however, be interpreted as apparent effects resulting from the fact that observations will be made using light (or other EM radiation), as well as an under-appreciation of the implications of postulate 1 above i.e. the relative and equivalent nature of all reference frames. There is, for example, a problem in relation to the common use of the term ‘speed of light’ when referring to humans traveling through space. Specifically, what is the speed that is being referred to, relative to? I fear that many physicists today would consider that a heretical question and all talk of exceeding c to be sacrilege. I just hope they don’t decide to try to implement an inquisition! It’s not that I am trying to contradict what Einstein was saying in his 1905 paper – his two postulates seem to me to represent astute observations that are very much worth pointing out. And no doubt every result that logically follows from them is correct. Perhaps the best way of determining what the exact nature of these outcomes might be is to employ that method of reasoning that Einstein himself was so fond of – specifically the thought experiment. In endeavouring to explore the possibility of exceeding c, let’s start by considering a very simple scenario.

​ Exceeding c made simple

We can imagine a situation where two spacecraft are together but then accelerate away from each other, with each employing an acceleration of 10 m/s2 as shown in the figure below. This is 1g, which is the acceleration we experience on Earth from the force of gravity – so it could easily be withstood by the astronauts on the spacecraft. It could also be easily attained, maintained, and monitored through the use of accelerometers on each craft. (For anybody unfamiliar with the nomenclature of mechanics/accelerations, this just means that relative to the starting point, the speed of the craft increases by 10 metres per second (m/s), every second.)

Two spacecraft each fire their motors and accelerate away from a start point at 1g. (Drawing by the author.)

In this case, after a period of 100 days, each would be travelling at 173,000 km/s relative to where they started from, as shown below (calculated using Newton’s laws of motion). They would, in fact, each be travelling at more than half the speed of light relative to the start point, and since they are moving in opposite directions, it seems that their relative speed would exceed c.

After 100 days the two spacecraft are still accelerating away from the start point at 1g; they then cut off their motors. It appears that they have now attained a relative velocity of 346,000 km/s (which is greater than c). (Drawing by the author.)

In this scenario, everything that has happened is well within the limits of what SR and classical mechanics say is possible, and yet, apparently, one person is travelling away from another at a speed in excess of that of light. My suggestion is that the reason why this appears possible, while most texts on SR imply that it is not, is that insufficient consideration is given to the implications of everything being relative. For example, much emphasis is placed on the effects of time dilation; but what if these are apparent rather than real and they are observed because of the limited and constant speed of light? Let’s consider an analogous situation of a black universe containing only air, where observations are made using sound waves. In such a universe we would measure the speed of sound as always constant and effects such as time dilation would appear to occur. Obviously, in this situation it could not be objectively shown that a moving object had aged less than a stationary one. Also, if it is believed that SRTD is real, then paradoxical situations arise that are hard if not impossible to resolve. To help illustrate what is meant by the equivalent nature of all reference frames, we can consider a famous paradox that concerns twins. By the way, I have some friends that you could call paradoxical twins – the difference being that the guys I am discussing below are flying around in spacecraft.

​ Paradoxical twins

“My sister and I, you will recollect, were twins, and you know how subtle are the links which bind two souls which are so closely allied.”    

- Sir Arthur Conan Doyle

Let’s imagine twins travelling while observing each other. If one twin were on a spacecraft (let’s call it spacecraft 1) and the other twin were on another spacecraft (called spacecraft 2 and moving relative to 1), then time dilation would be observed. (The time dilation would be different if one of the twins were on the Earth or on another planet such as Mars - because the spacecraft, the Earth, and Mars would all be expected to be moving relative to each other.)

If the twins in the two spacecraft mentioned above were to both fire their motors for, say, 50 days (rather than 100) they would reach a relative speed of 173,000 km/s (which is about 58% of c), so that SRTD (calculated using something called the ‘Lorentz function’) would indicate that the twin on spacecraft 1 would observe that time appears to slow down for the twin on spacecraft 2. If this slowing of time were real (rather than just observed), then if both spacecraft simultaneously turned around and fired their motors so that they came back together again and they were able to compare their clocks, twin 2’s clock would show that less time had elapsed than was shown on twin 1’s clock – meaning that twin 1 was now older than twin 2. However, because everything is relative (and in the above description the two spacecraft even accelerated by equal amounts) there is no reason why the roles of the two twins should not be reversed, so that the twin 1’s clock would be found to have less time elapsed that that of twin 2 i.e. twin 2 is the older one. Obviously, it is impossible for both of the twins to be younger than the other! This is a version of the famous ‘Twin Paradox’, which has been stated in a number of forms over the last century, and for which various resolutions have been suggested. One of these is to assume that the rocket engine is only fired on one spacecraft so that it undergoes accelerations that cause time dilation due to general relativity effects (GRTD). The problem with this explanation is that GRTD would not be sufficient to explain the time dilation calculated from the Lorentz equations – particularly if the spacecraft travels at very near the speed of light for a considerable time. Also, situations can be imagined where the accelerations (and therefore GRTD) experienced by both persons would be identical in magnitude and duration (as in the example described above). Thirdly, if you are saying that the time dilation was due to acceleration relativistic effects, then this is GRTD and so cannot form a proof for the existence of SRTD. Perhaps it was the latter observation that led to a YouTube video being posted which was entitled “Twin paradox: the real explanation (no math)”. I will not mention the speaker’s name – but you can look it up if you are interested. He seems to be a nice guy – he does an engaging talk – no doubt he is an accomplished physicist who is respected by his peers. To give a very brief summary of what he says in the talk – he asks us to consider three observers: A stationary relative to the Earth, B moving away from it and C toward it (from a distant point). His idea, in a nutshell, is that at the half-way point, where B and C pass, B could use a big sign to tell C what time has passed on his clock – then C could start his clock and measure the time he takes for the second half of the journey and when C reaches Earth he could again use a sign to tell A the sum of the time elapsed during the two halves of the journey. According to the speaker, this time will be less than the time that has passed on A’s clock since B left. The reason why the speaker goes to the trouble of having two travellers is to avoid the necessity of having the traveller accelerate when turning around and heading back to the Earth because he feels that the conventional explanation that it is this acceleration that causes time to slow for the traveller is wrong. There is only one slight problem with all of this – the speaker seems to have forgotten the first postulate of special relativity, which says that: “The laws of physics are identical in all inertial systems (i.e., non-accelerating frames of reference); and all velocities are measured relative to a specified frame of reference.” In other words, since there are no accelerations occurring, it is equally valid to say that B (or C) is stationary as it is to say that A is. If B were considered to be stationary, then A would be moving and so time would pass more slowly on A. It is clearly impossible for time to pass more slowly on B than A and to also pass more slowly on A than B. Therefore, to summarise, this explanation seems to me to provide absolutely no resolution for the Twin Paradox. None, zero, zilch! And if a respected PhD physicist, author and science communicator (who runs YouTube channels and gives TED@New York talks, conducts research in particle physics at Fermi National Accelerator Laboratory, is an adjunct professor of physics at the University of Notre Dame, was a co-discoverer of the top quark, has co-authored hundreds of research papers, and, get this, was a member of the team that discovered the Higgs boson in 2012!) apparently cannot provide a resolution for the Twin Paradox, then I must ask – who can?! But this speaker made things rather over-complicated in considering three observers. In reality, it can be expressed simply – if two travellers pass at high relative velocity, they might each subjectively observe the other to be slowing down, but later they can’t both turn out to be both older and younger than the other – such a concept is ludicrous. This would seem to lead inexorably to the conclusion that there is no adequate resolution to the Twin Paradox. Or … perhaps I’m wrong … if you can think of a convincing resolution, I would be glad to hear about it! If no such resolution emerges, it’s hard (at least for me), to conclude that the twins could re-join and discover that time had passed at a different rate for one than the other. Damn hard. There is no doubt that the SR time dilation effect is genuinely observed, but I am having a hard time believing it is an absolute and real phenomenon, rather than being relative and apparent.

Special relativity time dilation: girl leaves boy to fly off at very high speeds. When she returns will she find the boy has aged more than herself? (Illustration by the author.)

You know, I have spent many years searching through books, scientific papers, and ‘popular science’ online articles/videos, for a satisfactory resolution to the Twin Paradox; but so far have been sorely disappointed. Most books on special relatively that mention the paradox vouchsafe the idea that the twin who turns around, thereby undergoing an acceleration, will be the one who has aged less – and indeed, this is what our children are taught in ‘A’ level physics lessons in schools and colleges. But the esteemed and respected professor mentioned above, who has tremendous experience in physics research, tells us in a YouTube video that the acceleration explanation is wrong! He then goes on to offer his proposed resolution to the paradox involving three gentlemen; all moving at a constant speed relative to each other; you can see what I think of this proposal in the text above.

Being something of a sucker for punishment, I have also asked a number of people who fancy themselves as physicists (in some cases perhaps justifiably), about the Twin Paradox, but again I can’t report that I got anywhere in these enquiries. My reception was perhaps somewhat similar to what one could have expected from a particularly pious priest after asking something like: ‘if everyone goes to heaven after dying, isn’t it getting a bit crowded up there?’ No doubt they thought I was a heretic, but their ripostes to my suggestion that the Twin Paradox shows that SRTD cannot be a real effect, include repeatedly placing particular emphasis on the ‘maths of the Lorentz transformations’. I can’t help thinking that such comments comprise an effort to build a mystique around the subject. This is a fault that scientists can occasionally be subject to where they are essentially trying to say that: ‘you don’t understand this physics, because you don’t understand the complex maths that it is based on’. I must point out though, that here this doesn’t wash, because while the Lorentz transformations sound complex and esoteric, they are in fact based upon some very simple maths – so simple that any self-respecting GCSE maths student could understand them (I won’t go into the Lorentz transformations here, but the maths they are based on, which relates to observed effects due to the constant speed of light, can be found in nearly every book on special relativity).

Another favourite is to discuss at length the dynamics of particles that have been observed in, for example, particle collisions in the Large Hadron Collider at CERN - or perhaps the fact that some Italian researchers thought they had measured neutrinos travelling faster than c but now find they were not. Well sorry, but I wasn’t talking about neutrinos, hadrons, quarks, or any other quasi-physical particles on the quantum scale, I was talking about full-sized dudes flying around in spacecraft – very much on the man-sized scale. I pointed this out to one ‘physics communicator’ gentleman who replied with something like ‘the laws of physics apply in the same way to everything’. Well, excuse me but that sounds a little nonsensical, since there are many curious phenomena observed in quantum dynamics, which cannot be directly transferred to the macroscopic scale. For example, in quantum mechanics there is a peculiar phenomenon known as superposition , where two particles seem to be in two or more places or states at once. While I don’t doubt that experiments can be performed that demonstrate superposition really occurs for particles such as photons (quantum-sized elementary particles that make up light), I very much doubt whether the same could be said of, for example, a football!

Having said that, I was interested in the 2018 Scientific American report that a team of researchers in Israel and Japan proposed an experiment designed to: “enable scientists to sneak a glance at where a photon actually resides when it is placed in a superposition”. They go on to say: “They cannot say exactly what a superposition is without looking at it, but if they try to look at it, it disappears.” And “(the) photon made this bizarre, logic-defying sequence of disjointed appearances … at different times.” So perhaps I have, after all, observed superposition on the macroscopic scale – when watching the cats in my garden! Speaking of cats, another example of superposition is that of Schrödinger's cat, which is a thought experiment, imagined by Austrian-Irish physicist Erwin Schrödinger in 1935. The idea is that you place a cat in a box with a tiny bit of radioactive material. When the radioactive material decays, it triggers a radiation detector that causes a poison or explosion to be released that kills the cat. To summarise, according to quantum mechanics, a paradox arises in that the cat ends up both dead and alive at the same time.

Schrödinger’s cat – both alive and dead at the same time? (Illustration by the author.)

Apparently, Schrödinger developed the idea during the course of discussions with Albert Einstein to illustrate problems associated with the ‘Copenhagen’ (i.e. standard) interpretation of quantum mechanics applied to everyday objects, where it is said that according to quantum superposition a cat inside a box can be both alive and dead at the same time. I, in fact, have a tabby (who I rather unimaginatively named Tabby), who is fond of getting inside cardboard boxes. I would certainly be surprised if I were to open such a box and find Tabby within to be both alive and dead. From personal experience, I know that cats are capable of virtually anything, but I really feel this is going too far. Such a feline would presumably find herself in some kind of cat-limbo (whatever that may be like); and since cats have seven lives, would one need to conduct this experiment seven times before any meaningful conclusions could be drawn?

My cat Tabby – is in a box (above); but while in it she will surely always be either alive or dead – never both. I open the box and discover that she was actually alive! (Below.)

Tabby demonstrates how direct application of quantum mechanics to macroscopic objects is not really sensible. By the way, you may have noticed that it is the ubiquitous Amazon box. (Photographs by the author.)

Be that as it may, Schrödinger, with his alive and dead cat in a box, imagined something that provides a pretty good illustration of the problems of applying quantum mechanical conclusions to everyday macroscopic objects. I should quote it the next time someone offers analysis of dynamics on the quantum scale as evidence of what speed a human could reach in a spacecraft. Not only that, but I won’t be entirely satisfied that SRTD is a real phenomenon, rather than an apparent one, until I hear a convincing resolution to the Twin Paradox; and will continue to suspect it may be possible for humans to travel faster than c until I hear a convincing explanation of why the accelerations in the simple thought experiments described above, could not occur.

And the explanations would have to relate to the man-sized scale of the thought experiments rather than the quantum scale (accelerated quantum-scale particle analogies just will not do!) It may simply be that we have never observed macroscopic objects travelling faster than light since there are no known natural phenomena capable of accelerating them to such great speeds – combined, of course, with the fact that the fastest thing we have with which to measure such speeds is EM radiation (e.g. light), which itself cannot travel faster than c.

But that’s just what I am thinking – we need a debate in the wider scientific community. I hope that’s clear. Now I need a cup of tea.

Whatever speeds we eventually reach, there will always be time for tea. (Illustration by the author.)

Something in the air – or aether

“Once ether was everywhere. The crook of an arm, say. (Also, the heavens.) It slowed the movement of the stars, told the left hand where the right hand went. Then it was gone, like hysteria, like the hollow earth. The news came over the radio. There is only air now. Abandon your experiments.”

― Jenny Offill, Dept. of Speculation

The above discussion of the Twin Paradox provides an example of what is meant by one saying that, in considering SRTD, it seems that not enough consideration is generally given to the implications of postulate 1. It is possible that the reason for this is as follows: The concept of the aether as a type of medium or substance that is associated with an absolute coordinate frame, had been well established in the minds of scientists for some hundreds of years when, suddenly, the Michelson-Morley experiment effectively disproved its existence. Drat and blast! (As Dick Dastardly might have said.) Scientists don’t like surprises. However, it was also found that the speed of light is always constant in space (away from gravitational bodies) irrespective of the velocity of the light source. So, although the concept of an absolute aether was dismissed, scientists still thought of light as propagating through a ‘medium’ (although not a real substance); and some scientists even continued to identify the term aether with ‘properties of space’ that results in the constant value of c (this version of aether could be referred to as ‘virtual aether’). Since air, and the traditional aether, is located relative to an absolute reference frame, it may therefore have been assumed, at perhaps an unconscious level, that the virtual aether also somehow provides a reference frame for measuring velocities. This results in books/articles referring to a person travelling at, for example, less than or near to the speed of light, without giving information on what this ‘speed’ is being measured relative to. Sometimes the authors tend to imply that the speed they refer to is relative to the Earth, but relativity tells us that the location of the Earth cannot provide an absolute reference point, any more than the position of the Sun, or the centre of the Milky Way Galaxy could.

“If you ever start taking things too seriously, just remember that we are talking monkeys on an organic spaceship flying through the universe.”

― Joe Rogan

Books/articles on SR often also discuss the idea of a very fast moving spacecraft going through a ‘light-barrier’ and state that this is analogous to an aircraft passing through a sound barrier in air, and they go on to discuss potential problems associated with this. Again, this effect would be observed if the virtual aether had an absolute location as air does on Earth; whereas, in reality, the virtual aether (i.e. observation of light travelling at c), always behaves as though it were located relative to the point at which the light concerned is observed. Imagine a spacecraft travelling in interstellar space, at velocity near c relative to the Earth, while carrying a light source that is radiating visible light in all directions.

Spacecraft travelling away from an Earth observer (on left). (Drawing by the author.)

When the above spacecraft is travelling away from the Earth at 0.9c, everyone (or nearly everyone) agrees that both the craft and Earth observers would measure the light as travelling at a speed of c, with the only difference being that for the Earth observer the frequency of the light would appear to be red (Doppler) shifted.

If we imagine that the craft were now to fire its motor for a period so that it accelerated beyond c to, say, 1.1c relative to the Earth, and then turned off the motor, both the Earth and the craft would be in non-accelerating reference frames. Given this situation, according to the first postulate of SR, the light would continue to radiate equally in all directions as shown above (just as a similar light would on the Earth), and passage through a ‘light barrier’ would not, in fact, have been observed by those aboard the craft (ignoring starlight effects). Rather, it seems to me that the spacecraft observer would still measure the light as being emitted at a velocity of c; however, the Earth observer would no longer be able to see the light since the relative velocity of the craft is now greater than c.

The conclusion is surely that a good analogy cannot be made with the sound barrier, since the spacecraft is not moving relative to the virtual aether, unlike an aircraft moving relative to the air.

In the previous thought experiment, an object is described as moving away from the Earth at a speed greater than that of light. One would expect that most physicists would consider such a thing to be impossible, given that we are constantly being told that ‘nothing can travel faster than light’. Consequently, it may surprise you to learn that most, in fact, don’t – for the following reason. Scientists have taken measurements that show that the Universe is expanding and objects that are far away from us are travelling away from us at a faster speed than nearer ones. This is called ‘Hubble’s Law’ – where the velocity of the galaxies is been determined by their redshift - a Doppler shift of the light they emit towards the red end of the spectrum. Actually, recent observations with the Hubble Space Telescope show that not only is the Universe expanding, it’s doing so at an accelerating rate. In case you are interested, this was achieved by astronomers using Hubble’s images to observe a particular kind of supernovae (Type Ia supernovae) that are believed to have a uniform brightness. This allowed scientists to determine how far away each supernova was from its apparent brightness, while measuring its velocity using redshift. Their conclusion was that the rate of expansion of the universe is increasing.

Nobody is completely sure why this is, but it has been suggested that it is caused by a mysterious form of energy that scientists have named 'dark energy', which is possibly pushing everything apart. This, by the way, is not to be confused with ‘dark matter’, the latter being matter that has not been observed but which has been suggested as existing to explain why, for example, galaxies stay together rather than flying apart.

The impressive and ultimately highly successful Hubble Space Telescope; whose images have provided many discoveries, including the fact that the universe is expanding at an accelerating rate. (Illustration by the author.)

According to these theories, the total mass–energy of the universe comprises 68% dark energy, 27% dark matter, and only 5% ordinary matter and energy, with the latter being the only type we stand a chance of observing with our telescopes. Of course, another possibility is that all this dark energy and matter is humbug (as Scrooge would have said) and it’s just that we have something wrong with our current theories of gravity. Personally, I wouldn’t rule out the latter.

If you travel far enough out (way-out man!), there is a distance (beyond 15 billion light years) at which objects such as galaxies, are speeding away from us faster than the speed of light! Strange, but true, apparently. At the point at which they exceed c, they cross a cosmological event horizon , where the situation for them is very similar to the spacecraft in the above thought experiment, in that light from them would then not be able to reach us. It’s worth noting that if the idea of the ‘light barrier’ were correct, then presumably one would expect to see a flash of light when a body such as a galaxy passes through the cosmological event horizon (analogous to the sonic boom for the sound barrier), but I don’t believe any such effect is observed and I can’t help thinking this is for the reasons described above.

So, it is possible for objects to move apart at speeds greater than c after all – simply by them being sufficiently distant to travel fast enough to pass the cosmological event horizon. According to currently accepted physics, this can occur for very distant objects but not for closer ‘local’ ones. You may wonder why this is the case and if you were to ask a physicist this, they would probably reply by talking about ‘space-time curvature’ effects and general relativity – despite the fact that these relate to the slowing of light due to the presence of massive bodies in space. This is not something we are considering here – we are just talking about an object travelling away from an observer. Or they might say something like: ‘although the distant galaxies are moving, they are not actually moving – space is just expanding’. Wow I’ve got to try that if I get stopped by the police for speeding: “What can I do for you officer … speeding you say? No, I don’t think so, I wasn’t moving that fast – it was just the space between us expanding!” Sure-fire winner with the Boys in Blue, I’m sure. To summarise, saying that object A cannot move faster than c relative to the viewer but object B can, just because B is further away from the viewer than A, seems to me a bit far-fetched (as it were).

So, we have reason to believe that it is possible for objects such as very distant galaxies (that are about 13 to 15 billion light years from us), to travel at velocities of more than c relative to the Earth. Let’s now consider the situation for objects at distances that are less extreme. There are, of course, vast multitudes of bodies in space, including planets, stars, and galaxies – the above craft would be expected to be travelling at speeds of more than c relative to some and less than c relative to others – the Earth would simply comprise one of these bodies. For example, we can imagine a situation where the direction of the motion of the spacecraft is in a straight line directly towards the Andromeda Galaxy. If, when traveling at a speed of 0.999c, the rocket motor is turned off, then, according to Newton’s first law of mechanics, it would continue to move at 0.999c indefinitely (ignoring the gravitational effects of the galaxies and friction from occasional hydrogen atoms). I think nearly everyone would agree that this is a possible scenario. Let’s say that the craft travels in this way for, say, 100,000 (Earth) years – after such a long time it has left our Milky Way Galaxy. It’s now moving directly away from the Milky Way Galaxy and toward the Andromeda galaxy. Now, the Andromeda Galaxy is actually moving towards the Milky Way Galaxy (Andromeda is the closest large spiral galaxy to our own and is unusual for a very distant body, in that it is moving toward us). So, in this situation presumably the craft would be travelling at a speed of more than c relative to Andromeda. If you think it wouldn’t be, why?

Do you imagine that as it approached a speed of c relative to Andromeda, at which time it would be travelling at less than c relative to the Earth, its acceleration would suddenly reduce to zero? That seems a little unlikely, does it not? Beautiful Andromeda is, after all, considerably larger than the Milky Way and, of course, immensely larger than the Earth. The concept that the spacecraft cannot be travelling at a speed greater than c relative to any of the multitudinous objects in the observable Universe, many of which are themselves travelling at all kinds of speeds – some of which will, of course, be high, sounds to me to be ipso facto , on its face and by its nature, nuts! But again, you can decide for yourself. By the way, if you are wondering how anyone on the spacecraft would know for sure that the craft is accelerating, this is easily answered – they would, not surprisingly, use an accelerometer – the previously mentioned device that measures acceleration. You can buy simple versions of these devices from Amazon or eBay; connect them correctly and they will give you a reading of acceleration – and if you keep a record of your acceleration over time, you can work out your speed relative to the starting point (using Newton’s laws again).

Definition of c

“If any philosopher had been asked for a definition of infinity, he might have produced some unintelligible rigmarole, but he would certainly not have been able to give a definition that had any meaning at all.”

- Bertrand Russell

Another argument that is given for why humans cannot exceed the speed of light is that the Lorentz equations show that, for example, time would slow to zero as c was approached. Although, as described above, the Lorentz equations might only describe relative apparent effects, let us imagine that it were impossible to travel at c, but that travel at more or less than c were possible (it has, for example, been suggested that travel at precisely c is impossible because it would invalidate Maxwell’s equations). Even in this situation, we can imagine how it would be possible for an accelerating spacecraft to exceed c, for the following reasons: The speed of light (like any other speed) is an abstract concept; it is not real – it covers an infinitely small range of speeds. Therefore, the accelerating craft would spend an infinitely small period of time at exactly c, so that even if travel at exactly c were impossible, it would be possible to accelerate through and beyond it. It is also worth noting that quantum mechanics shows that all phenomena/energy changes at the sub-atomic scale occur in small packets – quanta. This explains why an energised electron can pass through forbidden orbits in order to reach possible higher energy orbits.

While we are discussing the exact nature of the speed of light, it is worth mentioning that nowadays it is based on a definition rather than observation. It has been defined to travel at exactly 299,792,458 metres per second. Rupert Sheldrake is, however, of the opinion that it changes somewhat over time, and points to a drop in speed observed between 1925 and 1950. It does seem, though, that his idea will remain untested for the foreseeable future, since the unit of length the metre is defined in terms of the speed of light, which of course is itself defined. (The metre is defined as the length of the path travelled by light in a vacuum during a time interval of 1/299 792 458 of a second.) Imagine if I had a car and was trying to measure the actual speed it travels at by dropping a marker, driving for 1 hour, and then dropping another marker. If I had defined my car to always travel at 50 miles per hour, I would say that the distance between the markers is 50 miles. If the actual speed were only 25 mph you might think that the distance between the markers would be 25 miles but, according to the definition, it would be 50 miles – so the situation would be ludicrous and I would never be able to measure the actual speed. What I am trying to say is that defining a physical phenomenon, such as the speed of light, as having a certain value, rather than actually measuring it, does not impress me as being very scientific, but again seems rather dogmatic. I am not, by the way, asserting that c does change because, Jesus, I’m likely to be in enough trouble as it is.

Experimental proof?

“No amount of experimentation can ever prove me right; a single experiment can prove me wrong.”

- Albert Einstein

It may be that Einstein was not quite right in regard to the above quote, since the single experiment of showing the bending of light from stars when the light rays pass close to the Sun, pretty much proved his general theory of relativity was correct (as mentioned above). But what about travelling faster than c? Physicists who believe that c cannot be exceeded, often point to experiments in particle accelerators as providing experimental evidence of its impossibility. Such machines employ electric/magnetic fields in order to accelerate particles to very high speeds. There can be little doubt that c has a particular significance in electromagnetism. Electromagnetic (EM) waves are comprised of oscillating electric and magnetic fields, and we all agree that EM waves are always observed as travelling at c – it seems they cannot travel faster than c. Is it then completely surprising that when using electric and magnetic fields to accelerate miniscule particles from rest, we are not able to accelerate them in this manner to speeds greater than c? Perhaps we should have expected that. But can we then make the inference, as most physicists do, that since we can’t accelerate the particles beyond c, it will therefore never be possible for men to travel in spacecrafts at speeds greater than c? I have my doubts. Curious phenomena are the rule rather than the exception on the quantum scale; and, as mentioned, we simply can’t expect dynamics observed in a particle accelerator to be the same as permitted behaviour on a macroscopic scale. (You remember Schrodinger’s perplexity about the cat in the box.) There is a world of difference between trying to use a stationary magnetic field to accelerate a barely physically existing particle/wave to c and someone cruising along in a spacecraft at 0.9c relative to some object, burning their rocket motor for a while with the result that their speed relative to the said object increased by 20%. I mentioned to one science communicator/journalist gentleman, that the mechanics of humans is not the same as the mechanics of sub-atomic, let along quantum scale, particles. The reason I said this is that he was referring to the physics of mesons, as part of his argument to say that humans cannot travel faster than c. When I pointed out that humans are rather different from mesons, seeing that the latter have a diameter of one femtometer (which, if you would like to know, is 1×10−15 m), he said something like: ‘the laws of physics apply in the same way to all objects’. He is probably a nice guy – no doubt he goes down to the pub with his mates and so on – but what kind of nonsense is that? Is he saying that, since everything is subject to the same laws of physics, it follows that all objects should behave in the same way? Surely not! A meson is, as a matter of fact, about the same size as a proton and, I must point out, the mechanical behaviour (as well as just about all other kinds of behaviour) of humans is completely different from that of mesons and protons. To summarise, it would have made more sense if, instead of a subatomic particle the size of a proton, he had been talking about something the size of a croton (a type of fairly large plant native to Indonesia, Malaysia, Australia, and the Western Pacific Ocean islands), or even a crouton (such as those that float in your soup).

By the way, uncharged mesons may decay to photons, which is a type of elementary particle. Photons are quantum particles/waves that make up electromagnetic radiation such as light and radio waves. They have no rest mass and they always move at the speed of light in vacuum. So, the journalist was arguing that mesons not being able to exceed c is evidence for humans not being able to do so, despite the fact that mesons decay into photons, which themselves always travel at the same speed – which is exactly the speed he believes humans cannot travel at! Make of that what you will; but, to be honest, it doesn’t prepossess me to place a pre-order on Amazon for the physics book he said he was writing (although naturally I wouldn’t be averse to receiving a complimentary copy – I always try to keep an open mind). One thing I will point out though, is that photons are the force carrier for electromagnetic force fields – meaning that it would not be exactly surprising that such fields cannot operate at relative speeds that exceed c.

Finally, it is often stated that experimental tests have been undertaken on aircraft that show that SRTD has caused highly accurate clocks on the aircraft to run more slowly than clocks on the ground – if this were the case, then it would provide evidence that SRTD were a real effect. Considering the importance of an ultimate limit to the speeds which humans could, in theory, reach and its implications for, say, galactic exploration and colonisation, the actual number of such experimental tests does seem relatively limited. The test that is often quoted was undertaken almost half a century ago. In 1972, J. C. Hafele, and R. E. Keating flew highly accurate caesium clocks around the world in both directions. Their measurements showed that the flying clocks gained and lost time relative to an Earth-based clock. (Whether they lost or gained time depended on their direction of travel and ‘lost time’ meant that upon return the flying clock indicated that less time had passed than was shown on the ground clock.) Despite this, I have doubts about whether the experiment can be taken as proof that SRTD is real, since, as you may recall, special relativity considers effects caused by velocities measured in frames of reference that are not accelerating and are away from the effects of gravity (hence the term ‘special’). This is not the case for the Hafele and Keating clocks – they are located on aircraft that are accelerating in circular paths around the Earth and they are, of course, subject to the Earth’s gravitational field. These results can, however, be explained in terms of general relativity effects: a clock will have the velocity of its plane added to the rotation of the Earth (or subtracted from it, depending upon the direction of travel). The resulting tangential velocity represents an acceleration of the flying clock relative to the one on the Earth, which will result in a GRTD effect. (Einstein’s equivalence principle states that gravity force is the same as the pseudo-force experienced by an observer in an accelerated frame of reference – so that both acceleration and gravity forces influence the rate at which time passes.) GRTD further indicates that both flying clocks will also experience a speed increase due to being further from the centre of the Earth than the ground clock. To summarise, my suggestion is that it’s possible that in this case the time dilation was real and that GRTD effects can explain the time differentials indicated by the clocks.  Therefore, when it is stated that taking a very accurate clock into an aircraft resulted in it running at a different speed to an identical one on the ground, and that this was caused by the velocity and height of the flying clock, this can be interpreted as being correct but misleading. The time differential might arise not from special relativity but from the general relativity effects associated with the acceleration and height of the flying clock. So, although such experiments do provide evidence that GRTD is a real effect, I would hesitate to say that they prove that SRTD is real. At least, that’s my perspective on things – and I’m sticking with it! Besides, if SRTD were a real objective phenomenon, then there would need to be a resolution to the Twin Paradox and, as discussed in detail above, such a resolution does not seem, at least so far, to exist.