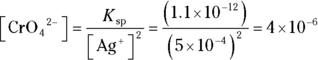Chapter 17
Achieving Neutrality with Titrations and Buffers
IN THIS CHAPTER
 Deducing the concentration of a mystery acid or base through titration
Deducing the concentration of a mystery acid or base through titration
 Working with buffered solutions
Working with buffered solutions
 Measuring the solubility of saturated solutions of salts with Ksp
Measuring the solubility of saturated solutions of salts with Ksp
In the real world of chemistry, acids and bases often meet in solution, and when they do, they’re drawn to one another. These unions of acid and base are called neutralization reactions because the lower pH of the acid and the higher pH of the base essentially cancel one another out, resulting in a neutral solution. In fact, when a hydroxide-containing base reacts with an acid (containing 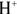 ), the products are simply an innocuous salt and water.
), the products are simply an innocuous salt and water.
Although strong acids and bases have their uses, the prolonged presence of a strong acid or base in an environment not equipped to handle it can be very damaging. In the laboratory, for example, you need to handle strong acids and bases carefully, deliberately performing neutralization reactions when appropriate. A lazy chemistry student who attempts to dump a concentrated acid or base down the laboratory sink will get a browbeating from her hawk-eyed teacher. Dumping stuff like this can damage the pipes and is generally unsafe. A responsible chemist neutralizes acidic laboratory waste with a base such as baking soda and neutralizes basic waste with an acid. Doing so makes a solution perfectly safe to dump down the drain and often results in the creation of a satisfyingly sizzly solution while the reaction is occurring.
In this chapter, we explore three issues that arise when acids meet up with bases:
- Titration: Titrations are the process by which chemists add acids to bases (or vice versa) a little bit at a time, gradually using up acid and base equivalents as the two neutralize each other. We show you how to use titration to figure out the concentration of an unknown acid.
- Buffer solutions: Buffer solutions are mixtures that contain both acid and base forms of the same compounds and serve to maintain the pH of the solution even when extra acid or base is added.
- Solubility product: Because salts are produced when acids react with bases, we discuss the solubility product,
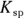 , a number that tells you how soluble a salt is in solution.
, a number that tells you how soluble a salt is in solution.
 At heart, neutralization reactions in which the base contains a hydroxide ion are simple double-replacement reactions of the form
At heart, neutralization reactions in which the base contains a hydroxide ion are simple double-replacement reactions of the form 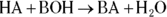 (in other words, an acid reacts with a base to form a salt and water). You’re asked to write a number of such reactions in this chapter, so be sure to review double replacement reactions and balancing equations in Chapter 8 before you delve into the new and exciting world of neutralization.
(in other words, an acid reacts with a base to form a salt and water). You’re asked to write a number of such reactions in this chapter, so be sure to review double replacement reactions and balancing equations in Chapter 8 before you delve into the new and exciting world of neutralization.
Concentrating on Titration to Figure Out Molarity
Imagine you’re a newly hired laboratory assistant who’s been asked to alphabetize the chemicals on the shelves of a chemistry laboratory during a lull in experimenting. As you reach for the bottle of sulfuric acid, your first-day jitters get the better of you, and you knock over the bottle. Some careless chemist failed to screw the cap on tightly! You quickly neutralize the acid with a splash of baking soda and wipe up the now nicely neutral solution. As you pick up the bottle, however, you notice that the spilled acid burned away most of the label! You know it’s sulfuric acid, but there are several different concentrations of sulfuric acid on the shelves, and you don’t know the molarity of the solution in this bottle. Knowing that your boss will surely blame you if she sees the damaged bottle and not wanting to get sacked on your very first day, you quickly come up with a way to determine the molarity of the solution and save your job.
You know that the bottle contains sulfuric acid of a mystery concentration, and you notice bottles of 1 M sodium hydroxide, a strong base, and phenolphthalein, a pH indicator, among the chemicals on the shelves. You measure a small amount of the mystery acid into a beaker and add a little phenolphthalein. You reason that if you drop small amounts of sodium hydroxide into the solution until the phenolphthalein indicates that the solution is neutral by turning the appropriate color, you’ll be able to figure out the acid’s concentration.
You can find the concentration by doing a simple calculation of the number of moles of sodium hydroxide you’ve added and then reasoning that the mystery acid must have an equal number of moles to have been neutralized. This then leads to the number of moles of acid, and that, in turn, can be divided by the volume of acid you added to the beaker to get the molarity. Whew! You relabel the bottle and rejoice in the fact that you can come in and do menial labor in the lab again tomorrow.
 This process is called a titration, and it’s often used by chemists to determine the molarity of acids and bases. In a titration calculation, you generally know the identity of an acid or base of unknown concentration, and you know the identity and molarity of the acid or base that you’re going to use to neutralize it. Given this information, you then follow six simple steps:
This process is called a titration, and it’s often used by chemists to determine the molarity of acids and bases. In a titration calculation, you generally know the identity of an acid or base of unknown concentration, and you know the identity and molarity of the acid or base that you’re going to use to neutralize it. Given this information, you then follow six simple steps:
- Measure out a small volume of the mystery acid or base.
-
Add a pH indicator such as phenolphthalein to the mystery acid or base.
Different pH indicators involve different color changes. Make sure you know which color the solution will turn when it reaches the equivalence point.
-
Neutralize.
Slowly add the acid or base of known concentration to the solution until the indicator shows that the solution is neutral, keeping careful track of the volume added.
-
Calculate the number of moles added.
Multiply the number of liters of acid or base added by the molarity of that acid or base to get the number of moles you added.
-
Calculate the unknown moles.
Use the balanced equation and basic stoichiometry to determine how many moles of the mystery substance being neutralized are present (see Chapter 9 for details on stoichiometry).
-
Solve for molarity.
Divide the number of moles of the mystery acid or base by the number of liters measured out in Step 1, giving you the molarity.
People often visualize the titration process using a graph that shows the concentration of base on one axis and the pH on the other, as in Figure 17-1. The interaction of the two concentrations traces out a titration curve, which has a characteristic s shape. At the equivalence point in Figure 17-1, the amount of base present is equal to the amount of acid present in the solution. If you’re using an indicator such as phenolphthalein, the equivalence point marks when the first permanent color change takes place.
 Q. If the laboratory assistant had to add 10 mL of 1 M sodium hydroxide to neutralize 5 mL of the sulfuric acid in his impromptu titration, what did he end up writing on the label for the concentration of the sulfuric acid in the bottle?
Q. If the laboratory assistant had to add 10 mL of 1 M sodium hydroxide to neutralize 5 mL of the sulfuric acid in his impromptu titration, what did he end up writing on the label for the concentration of the sulfuric acid in the bottle?
A. 1 M H2SO4. The problem tells you that the volume from Step 1 of the titration process is 5 mL and that the volume of base from Step 3 is 10 mL. In Step 4, you must calculate the number of moles of sodium hydroxide the lab assistant added by multiplying the volume in liters (0.01 L) by the molarity (1 M) to give you 0.01 mol NaOH. The balanced equation for this reaction is
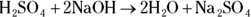
You use the coefficients from this equation along with the mole value calculated in Step 4 to determine the mole value of the unknown substance you’re titrating:
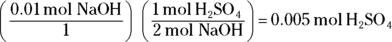
The final step is to divide this value by the liters of acid added to get the molarity. Your initial acid volume was given as 5 mL, which converts to 0.005 L.
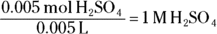
The assistant should have labeled the bottle as 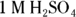 .
.
1 In doing a titration of a solution of calcium hydroxide of unknown concentration, a student adds 12 mL of 2 M HCl (hydrochloric acid) and finds that the molarity of the base is 1.25 M. How much 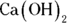 must the student have measured out at the start of the titration?
must the student have measured out at the start of the titration?
2 Titration shows that a 5.0 mL sample of nitrous acid, HNO2, has a molarity of 0.50. If 8.0 mL of magnesium hydroxide, 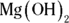 , was added to the acid to accomplish the neutralization, what must the molarity of the base have been?
, was added to the acid to accomplish the neutralization, what must the molarity of the base have been?
3 How much could a chemist find out about a mystery acid or base through titration if neither its identity nor its concentration is known?
Maintaining Your pH with Buffers
You may have noticed that the titration curve shown in Figure 17-1 has a flattened area in the middle where pH doesn’t change significantly as base is added. This region is called a buffer region.
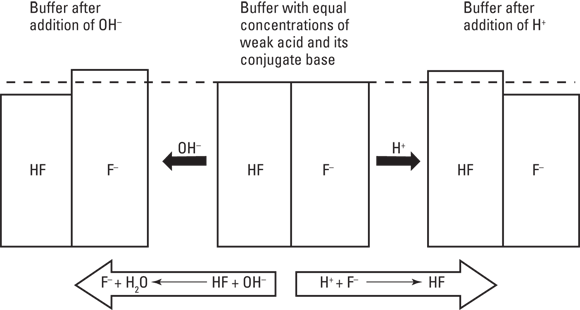
Certain solutions, called buffered solutions, resist changes in pH like a stubborn child resists eating her Brussels sprouts: steadfastly at first but choking them down reluctantly if enough pressure is applied (such as the threat of no dessert). Although buffered solutions maintain their pH very well when relatively small amounts of acid or base are added to them or the solution is diluted, they can withstand the addition of only a certain amount of acid or base before becoming overwhelmed.
Buffers are most often made up of a weak acid and its conjugate base, though they can also be made of a weak base and its conjugate acid. (Conjugate bases and acids are the products in acid-base reactions; see Chapter 16 for details.) A weak acid in aqueous solution will be partially dissociated, and the amount of dissociation depends on its pKa value (the negative logarithm of its acid dissociation constant). The dissociation will be of the form 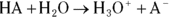 , where
, where 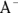 is the conjugate base of the acid HA. The acidic proton is taken up by a water molecule, forming hydronium. If HA were a strong acid, approximately 100 percent of the acid would become
is the conjugate base of the acid HA. The acidic proton is taken up by a water molecule, forming hydronium. If HA were a strong acid, approximately 100 percent of the acid would become 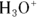 and
and 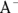 , but because it’s a weak acid, only a fraction of the HA dissociates and the rest remains HA.
, but because it’s a weak acid, only a fraction of the HA dissociates and the rest remains HA.
The Ka of this reaction is defined by
Solving this equation for the 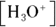 concentration allows you to devise a relationship between the
concentration allows you to devise a relationship between the 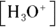 and the
and the 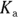 of a buffer:
of a buffer:
 Taking the negative logarithm of both sides of the equation and manipulating logarithm rules yields an equation called the Henderson-Hasselbalch equation, which relates the pH and the
Taking the negative logarithm of both sides of the equation and manipulating logarithm rules yields an equation called the Henderson-Hasselbalch equation, which relates the pH and the 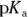 :
:
With logarithm rules, you can manipulate this equation to get 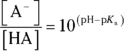 , which may be more useful in certain situations.
, which may be more useful in certain situations.
 The very best buffers and those best able to withstand the addition of both acid and base are those for which [HA] and
The very best buffers and those best able to withstand the addition of both acid and base are those for which [HA] and 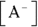 are approximately equal. When this occurs, the logarithmic term in the Henderson-Hasselbalch equation disappears, and the equation becomes
are approximately equal. When this occurs, the logarithmic term in the Henderson-Hasselbalch equation disappears, and the equation becomes 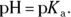 When creating a buffered solution, chemists therefore choose an acid that has a pKa close to the desired pH.
When creating a buffered solution, chemists therefore choose an acid that has a pKa close to the desired pH.
If you add a strong base such as sodium hydroxide (NaOH) to this mixture of dissociated base (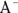 ) and undissociated acid (HA), the base’s hydroxide is absorbed by the acidic proton, replacing the exceptionally strong base
) and undissociated acid (HA), the base’s hydroxide is absorbed by the acidic proton, replacing the exceptionally strong base  with a relatively weak base
with a relatively weak base 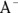 and minimizing the change in pH:
and minimizing the change in pH:
This causes a slight excess of base in the reaction, but it doesn’t affect pH significantly. You can think of the undissociated acid as a reservoir of protons that are available to neutralize any strong base that may be introduced to the solution. As we explain in Chapter 14, when a product is added to a reaction, the equilibrium in the reaction changes to favor the reactants or to “undo” the change in conditions. Because this reaction generates 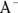 , the acid dissociation reaction happens less frequently as a result, further stabilizing the pH.
, the acid dissociation reaction happens less frequently as a result, further stabilizing the pH.
When a strong acid, such as hydrochloric acid (HCl), is added to the mixture, its acidic proton is taken up by the base 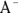 , forming HA:
, forming HA:
This causes a slight excess of acid in the reaction but doesn’t affect pH significantly. It also shifts the balance in the acid dissociation reaction in favor of the products, causing it to happen more frequently and re-creating the base 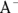 .
.
Figure 17-2 summarizes the addition of acid and base and their effect on the ratio of products and reactants.
Buffers have their limits, however. The acid’s proton reservoir, for example, can compensate for the addition of only a certain amount of base before it runs out of protons that can neutralize free hydroxide. At this point, a buffer has done all it can do, and the titration curve resumes its steep upward slope.
4 Ethanoic acid would make an ideal buffer to maintain what approximate pH?
5 Describe the preparation of 1,000 mL of a 0.2 M carbonic acid buffer of 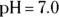 . Assume the
. Assume the 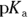 of carbonic acid is 6.8.
of carbonic acid is 6.8.
Measuring Salt Solubility with 
In chemistry, a salt is not necessarily the substance you sprinkle on french fries. Rather, a salt is any substance that is a combination of an anion and a cation and is created in a neutralization reaction. Salts, therefore, tend to dissociate in water. The degree of dissociation possible — in other words, the solubility of the salt — varies greatly from one salt to another.
 Chemists use a quantity called the solubility product constant, or
Chemists use a quantity called the solubility product constant, or 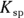 , to compare the solubilities of salts.
, to compare the solubilities of salts. 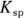 is calculated in much the same way as an equilibrium constant (
is calculated in much the same way as an equilibrium constant (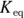 ; see Chapter 14). The product concentrations are multiplied together, each raised to the power of its coefficient in the balanced dissociation equation. There’s one key difference, however, between a
; see Chapter 14). The product concentrations are multiplied together, each raised to the power of its coefficient in the balanced dissociation equation. There’s one key difference, however, between a 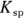 and a
and a 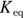 .
. 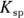 is a quantity specific to a saturated solution of salt, so the concentration of the undissociated salt reactant has absolutely no bearing on its value. If the solution is saturated, then the amount of possible dissociation is at its maximum, and any additional solute added merely settles on the bottom.
is a quantity specific to a saturated solution of salt, so the concentration of the undissociated salt reactant has absolutely no bearing on its value. If the solution is saturated, then the amount of possible dissociation is at its maximum, and any additional solute added merely settles on the bottom.
6 Write the solubility product dissociation constants for silver (I) chromate (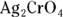 ) and strontium sulfate (
) and strontium sulfate (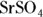 ).
).
7 If the 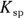 of silver (I) chromate is
of silver (I) chromate is 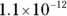 and the silver ion concentration in the solution is 0.0005 M, what is the chromate concentration?
and the silver ion concentration in the solution is 0.0005 M, what is the chromate concentration?
Answers to Questions on Titrations and Buffers
Following are the answers to the practice problems presented in this chapter.
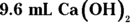 . Begin by finding the number of moles of HCl by multiplying the molarity (2 M) by the volume (0.012 L) to get 0.024 mol HCl. Next, calculate the number of moles of
. Begin by finding the number of moles of HCl by multiplying the molarity (2 M) by the volume (0.012 L) to get 0.024 mol HCl. Next, calculate the number of moles of 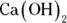 needed to neutralize this amount using the balanced chemical equation
needed to neutralize this amount using the balanced chemical equation 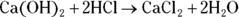 :
:
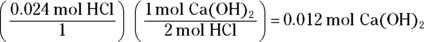
Divide this number by the molarity of the base to get the volume of base added:
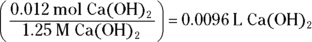
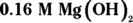 . This problem gives you Step 6 in the titration procedure and asks you to back-solve for the molarity of the base. Start by finding the number of moles of acid present in the solution by multiplying the molarity (0.50 M) by the volume (0.005 L), giving you 0.0025 mol. Next, examine the balanced neutralization reaction to determine the number of moles of magnesium hydroxide needed to neutralize
. This problem gives you Step 6 in the titration procedure and asks you to back-solve for the molarity of the base. Start by finding the number of moles of acid present in the solution by multiplying the molarity (0.50 M) by the volume (0.005 L), giving you 0.0025 mol. Next, examine the balanced neutralization reaction to determine the number of moles of magnesium hydroxide needed to neutralize 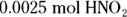 :
:

From the balanced equation, you can see that for every 2 mol of 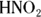 you need 1 mol of magnesium hydroxide to neutralize it:
you need 1 mol of magnesium hydroxide to neutralize it:
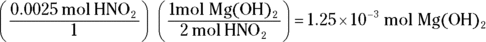
Divide this value by the volume of base added (8.0 mL, or 0.008 L) to get the molarity:
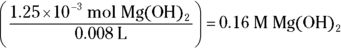
- Without an identity or a concentration, a chemist could still determine the number of moles per liter of the mystery acid or base. If he titrates an extra-mysterious acid with a base of known concentration until he achieves neutrality, then he knows the number of moles of acid in the solution (equal to the number of moles of base added). This information may even allow him to guess at its identity.
- pH of 4.7. Ethanoic acid, also known as acetic acid or vinegar, would be an ideal buffer for a pH close to its
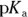 value. You’re given the
value. You’re given the 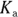 of ethanoic acid in the example problem (it’s
of ethanoic acid in the example problem (it’s 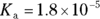 ), so simply take the negative logarithm of that value to get your
), so simply take the negative logarithm of that value to get your 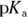 value and therefore your pH:
value and therefore your pH:
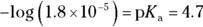
- You’re given a pH and a
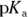 , which suggests that you need to use the Henderson-Hasselbalch equation. You have the total concentration of acid and conjugate base, but you don’t know either of the concentrations in the equation individually, so begin by solving for their ratio:
, which suggests that you need to use the Henderson-Hasselbalch equation. You have the total concentration of acid and conjugate base, but you don’t know either of the concentrations in the equation individually, so begin by solving for their ratio:
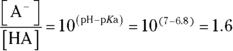
So you have 1.6 mol of base for every 1 mol of acid. Expressing the amount of base as a fraction of the total amount of acid and base therefore gives you
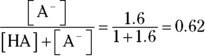
Multiply this number by the molarity of the solution (0.2 M) to give you the molarity of the basic solution, or 0.12 M. The molarity of the acid is therefore 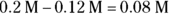 .
.
This means that to prepare the buffer, you must take 0.2 mol of carbonic acid and add it to somewhat less than 1,000 mL of water (say, 800 mL). To this you must add enough of a strong base such as sodium hydroxide (NaOH) to force the proper proportion of the carbonic acid solution to dissociate into its conjugate base. Because you want to achieve a base concentration of 0.12 M, you should add 120 mL of NaOH. Finally, you should add enough water to achieve your final volume of 1,000 mL.
- For silver (I) chromate:
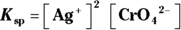 ; for strontium sulfate:
; for strontium sulfate: 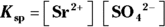 . To determine the solubility product constants of these solutions, you first need to write an equation for their dissociation in water (see Chapter 8 for details):
. To determine the solubility product constants of these solutions, you first need to write an equation for their dissociation in water (see Chapter 8 for details):
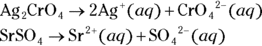
Raising the concentration of the products to the power of their coefficients in these balanced reactions yields the 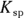 for each:
for each:
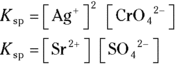
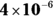 . You write an expression for the
. You write an expression for the 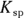 of silver (I) chromate in Problem 6. Solve the equation for the chromate concentration by dividing
of silver (I) chromate in Problem 6. Solve the equation for the chromate concentration by dividing 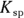 by the silver ion concentration:
by the silver ion concentration:
 Deducing the concentration of a mystery acid or base through titration
Deducing the concentration of a mystery acid or base through titration Working with buffered solutions
Working with buffered solutions Measuring the solubility of saturated solutions of salts with Ksp
Measuring the solubility of saturated solutions of salts with Ksp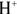 ), the products are simply an innocuous salt and water.
), the products are simply an innocuous salt and water. , a number that tells you how soluble a salt is in solution.
, a number that tells you how soluble a salt is in solution. At heart, neutralization reactions in which the base contains a hydroxide ion are simple double-replacement reactions of the form
At heart, neutralization reactions in which the base contains a hydroxide ion are simple double-replacement reactions of the form 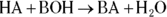 (in other words, an acid reacts with a base to form a salt and water). You’re asked to write a number of such reactions in this chapter, so be sure to review double replacement reactions and balancing equations in
(in other words, an acid reacts with a base to form a salt and water). You’re asked to write a number of such reactions in this chapter, so be sure to review double replacement reactions and balancing equations in  This process is called a titration, and it’s often used by chemists to determine the molarity of acids and bases. In a titration calculation, you generally know the identity of an acid or base of unknown concentration, and you know the identity and molarity of the acid or base that you’re going to use to neutralize it. Given this information, you then follow six simple steps:
This process is called a titration, and it’s often used by chemists to determine the molarity of acids and bases. In a titration calculation, you generally know the identity of an acid or base of unknown concentration, and you know the identity and molarity of the acid or base that you’re going to use to neutralize it. Given this information, you then follow six simple steps: 
 Q. If the laboratory assistant had to add 10 mL of 1 M sodium hydroxide to neutralize 5 mL of the sulfuric acid in his impromptu titration, what did he end up writing on the label for the concentration of the sulfuric acid in the bottle?
Q. If the laboratory assistant had to add 10 mL of 1 M sodium hydroxide to neutralize 5 mL of the sulfuric acid in his impromptu titration, what did he end up writing on the label for the concentration of the sulfuric acid in the bottle?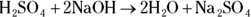
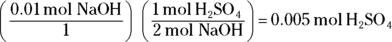
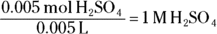
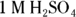 .
.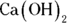 must the student have measured out at the start of the titration?
must the student have measured out at the start of the titration?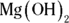 , was added to the acid to accomplish the neutralization, what must the molarity of the base have been?
, was added to the acid to accomplish the neutralization, what must the molarity of the base have been?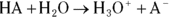 , where
, where 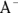 is the conjugate base of the acid HA. The acidic proton is taken up by a water molecule, forming hydronium. If HA were a strong acid, approximately 100 percent of the acid would become
is the conjugate base of the acid HA. The acidic proton is taken up by a water molecule, forming hydronium. If HA were a strong acid, approximately 100 percent of the acid would become 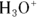 and
and 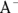 , but because it’s a weak acid, only a fraction of the HA dissociates and the rest remains HA.
, but because it’s a weak acid, only a fraction of the HA dissociates and the rest remains HA.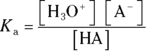
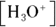 concentration allows you to devise a relationship between the
concentration allows you to devise a relationship between the 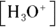 and the
and the 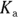 of a buffer:
of a buffer: 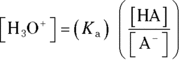
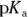 :
: 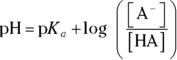
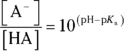 , which may be more useful in certain situations.
, which may be more useful in certain situations.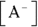 are approximately equal. When this occurs, the logarithmic term in the Henderson-Hasselbalch equation disappears, and the equation becomes
are approximately equal. When this occurs, the logarithmic term in the Henderson-Hasselbalch equation disappears, and the equation becomes 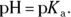 When creating a buffered solution, chemists therefore choose an acid that has a pKa close to the desired pH.
When creating a buffered solution, chemists therefore choose an acid that has a pKa close to the desired pH.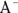 ) and undissociated acid (HA), the base’s hydroxide is absorbed by the acidic proton, replacing the exceptionally strong base
) and undissociated acid (HA), the base’s hydroxide is absorbed by the acidic proton, replacing the exceptionally strong base  with a relatively weak base
with a relatively weak base 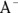 and minimizing the change in pH:
and minimizing the change in pH: 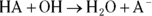
 , the acid dissociation reaction happens less frequently as a result, further stabilizing the pH.
, the acid dissociation reaction happens less frequently as a result, further stabilizing the pH. , forming HA:
, forming HA: 
 .
.
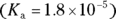 and its conjugate base, ethanoate. If the concentration of the solution is 0.5 M with respect to ethanoic acid and 0.3 M with respect to ethanoate, what is the pH of the solution?
and its conjugate base, ethanoate. If the concentration of the solution is 0.5 M with respect to ethanoic acid and 0.3 M with respect to ethanoate, what is the pH of the solution?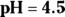 . This problem is a simple application of the Henderson-Hasselbalch equation. Remember to take the negative logarithm of Ka to get
. This problem is a simple application of the Henderson-Hasselbalch equation. Remember to take the negative logarithm of Ka to get 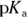 . Plugging in known values yields
. Plugging in known values yields 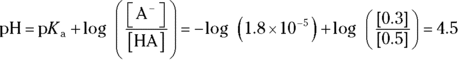
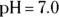 . Assume the
. Assume the 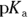 of carbonic acid is 6.8.
of carbonic acid is 6.8.
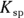 , to compare the solubilities of salts.
, to compare the solubilities of salts. 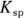 is calculated in much the same way as an equilibrium constant (
is calculated in much the same way as an equilibrium constant (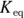 ; see
; see 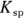 and a
and a 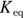 .
. 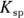 is a quantity specific to a saturated solution of salt, so the concentration of the undissociated salt reactant has absolutely no bearing on its value. If the solution is saturated, then the amount of possible dissociation is at its maximum, and any additional solute added merely settles on the bottom.
is a quantity specific to a saturated solution of salt, so the concentration of the undissociated salt reactant has absolutely no bearing on its value. If the solution is saturated, then the amount of possible dissociation is at its maximum, and any additional solute added merely settles on the bottom.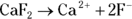 .
.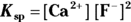 . You construct the solubility product constant by raising the concentrations of the two products to the power of their coefficients, so
. You construct the solubility product constant by raising the concentrations of the two products to the power of their coefficients, so 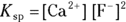 .
.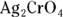 ) and strontium sulfate (
) and strontium sulfate (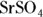 ).
).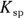 of silver (I) chromate is
of silver (I) chromate is 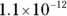 and the silver ion concentration in the solution is 0.0005 M, what is the chromate concentration?
and the silver ion concentration in the solution is 0.0005 M, what is the chromate concentration?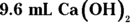 . Begin by finding the number of moles of HCl by multiplying the molarity (2 M) by the volume (0.012 L) to get 0.024 mol HCl. Next, calculate the number of moles of
. Begin by finding the number of moles of HCl by multiplying the molarity (2 M) by the volume (0.012 L) to get 0.024 mol HCl. Next, calculate the number of moles of 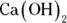 needed to neutralize this amount using the balanced chemical equation
needed to neutralize this amount using the balanced chemical equation 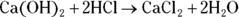 :
:
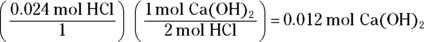
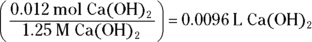
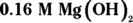 . This problem gives you Step 6 in the titration procedure and asks you to back-solve for the molarity of the base. Start by finding the number of moles of acid present in the solution by multiplying the molarity (0.50 M) by the volume (0.005 L), giving you 0.0025 mol. Next, examine the balanced neutralization reaction to determine the number of moles of magnesium hydroxide needed to neutralize
. This problem gives you Step 6 in the titration procedure and asks you to back-solve for the molarity of the base. Start by finding the number of moles of acid present in the solution by multiplying the molarity (0.50 M) by the volume (0.005 L), giving you 0.0025 mol. Next, examine the balanced neutralization reaction to determine the number of moles of magnesium hydroxide needed to neutralize 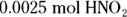 :
:

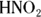 you need 1 mol of magnesium hydroxide to neutralize it:
you need 1 mol of magnesium hydroxide to neutralize it: 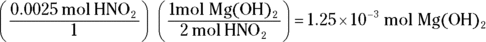
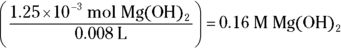
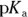 value. You’re given the
value. You’re given the 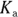 of ethanoic acid in the example problem (it’s
of ethanoic acid in the example problem (it’s 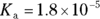 ), so simply take the negative logarithm of that value to get your
), so simply take the negative logarithm of that value to get your 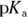 value and therefore your pH:
value and therefore your pH:
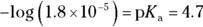
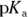 , which suggests that you need to use the Henderson-Hasselbalch equation. You have the total concentration of acid and conjugate base, but you don’t know either of the concentrations in the equation individually, so begin by solving for their ratio:
, which suggests that you need to use the Henderson-Hasselbalch equation. You have the total concentration of acid and conjugate base, but you don’t know either of the concentrations in the equation individually, so begin by solving for their ratio:
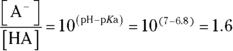
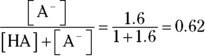
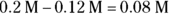 .
.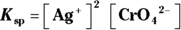 ; for strontium sulfate:
; for strontium sulfate: 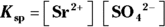 . To determine the solubility product constants of these solutions, you first need to write an equation for their dissociation in water (see
. To determine the solubility product constants of these solutions, you first need to write an equation for their dissociation in water (see 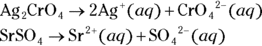
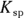 for each:
for each: 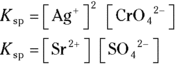
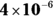 . You write an expression for the
. You write an expression for the 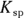 of silver (I) chromate in Problem 6. Solve the equation for the chromate concentration by dividing
of silver (I) chromate in Problem 6. Solve the equation for the chromate concentration by dividing 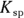 by the silver ion concentration:
by the silver ion concentration: