We may not realize it, but we humans are constantly ranking things: the food we buy in the grocery, the clothes we wear each day, the route we drive to work, the TV programs we watch, the sections of the newspaper we read, and so on. Like most of what we do mentally, this ranking is an unconscious but instinctive process that facilitates (perhaps even enables) our decision making. Because these everyday decisions are unconscious, we aren’t aware that they involve ranking. To rank means to assign a position to something relative to other things. In deciding what to wear to work in the morning, we open our closet, scan our wardrobe, eye several different outfits or suits, and select one. Is that ranking? Absolutely! We select—prefer—one article over the others; that is, we rank it higher and them lower. Our instinctive (we’re born with it) ability to rank things quickly and effortlessly is indeed a blessing. As with our other mental traits, we would be in serious trouble making decisions without this built-in software for ranking.
A simple exercise in ranking movies will serve to demonstrate our instinctive method. I have selected movies as the subject because your preference in movies is highly subjective, even arbitrary, and you have no stake in the rankings. Therefore, your method of ranking and the decisions you make won’t be distorted or hamstrung by concerns about putting the movies into the “right” order. There is no right or wrong order here. Whatever you think and feel about each movie is correct.
In a column on a sheet of paper write fifteen movies you have seen and about which you can make reasoned judgments. The list below will give you some ideas.
Now rank these fifteen movies from best to worst according to your personal likes and dislikes.
BEFORE CONTINUING, LIST AND RANK 15 MOVIES.
On a second sheet of paper, copy the matrix in Figure 10-1. In the first column, write in your fifteen movies as you initially listed them. I have entered my own list of movies as an example. Enter your rankings in the next column, as I have done with mine, and write “Instinctive Ranking” at the head of that column.
BEFORE CONTINUING, CONSTRUCT A MATRIX AND ENTER FIFTEEN MOVIES AND THEIR RANKINGS.
FIGURE 10-1
Now, on a separate sheet of paper, write down the reason(s) why you ranked your top choice at the top. Then write down the reason(s) why you ranked your bottom choice at the bottom.
BEFORE CONTINUING, WRITE THE REASONS FOR YOUR TOP AND BOTTOM CHOICES.
I would guess that the reason(s) you gave for making your top and bottom choices are distinctly different. For example, you may have put The Silence of the Lambs first because you love scary movies and put From Here to Eternity last because you dislike black-and-white films. “What’s wrong with that?” you ask. “After all, these are legitimate reasons: Silence is scary and Eternity is in black and white.” That’s true enough, but there are other factors—other criteria—to be considered. Scariness and film color are only two.
The main defect in our instinctive method lies in our tendency (addressed in Chapter 1 ) to view problems one-dimensionally… to focus on (glom on to) the first solution that makes sense, that offers an explanation. Thus, the moment we think of a reason—any sound, persuasive reason—to like or dislike one of the movies on our list, we tend to latch on to that reason, make our ranking decision on that basis, and move on without considering our other likes and dislikes, which may actually be more important to us.
Imagine ten female dancers standing side by side at the rear of a stage waiting to audition for selection for a chorus line in a Broadway musical. The dance director walks onto the stage, glances at the line of dancers, instantly points at a lanky blonde, and announces, “You’re first!” As that dancer steps to the center of the stage to demonstrate her talents, the director quickly surveys the line again and, nodding to a short brunette, declares, “You may go! We won’t need you.” Crestfallen, the dancer leaves, while the director, retreating several paces, begins to study the remaining candidates with great care, striding up and down the line, first in front, then behind. She* stops and crosses her arms, pondering her next decision.
What are all of the yet-to-be-chosen dancers thinking about at that moment? I’ll tell you. They’re trying to guess what the director saw in the dancer chosen first and the one sent home. They’re thinking, “Should I stand up straight to look taller? Is my goose cooked because I’m a brunette? Should I smile? Should I look her in the eye? Is my makeup too heavy?” Each is trying to guess what criteria the director used in making her first two selections.
The director picked the lanky blonde first because she was strikingly attractive and had a well-proportioned figure and slender legs, perfect for a chorus line. The director sent the brunette packing because her overly high forehead made her look bald. But whereas the criteria the director used for her first two decisions were clear-cut, the water quickly muddied when she considered the other candidates. Some had slender legs but chunky figures; some had chunky legs but slender figures; some faces were bland, some distinctive. It was difficult ranking one over another. So she was forced to come up with other rationales—other criteria — on which to make her decisions.
We all do the same thing when we rank things, such as when we select a place in which to reside. We survey several neighborhoods and dislike this one because the traffic is too heavy, like that one because it’s close to an elementary school, dislike this one because it lacks city sewers, like that one because the residences are attractive and well kept, and so on. We make our decision and, after moving in, are disappointed because the roof of the house leaks and the heating bills are too expensive. It is well and good to use stringent criteria in making decisions, but we should be sure we have considered all relevant criteria and have applied all of the criteria equitably to all of the decisions. As for the dance director, she ultimately dismissed the lanky blonde; although she was a talented dancer, she couldn’t remember the dance routines.
By applying different criteria to different ranking decisions, we distort our analysis, which can lead to gravely disappointing outcomes that later make us wonder what went wrong.
This phenomenon was brought home to me when my wife and I spent a couple of days in North Carolina looking at possible sites on which to build a home. As we went from one lot to another, we noted the acreage, whether city sewers were available, where the house would best be situated, whether the rear of the house would face south, and so on. As the day went on, we focused more and more on the landscape —the number, kinds, and placement of trees and bushes. When we returned to our hotel to mull over our findings, we discovered that we had eliminated several otherwise attractive lots simply because the landscape was not ideal. Suspecting that something was wrong with our methodology, we wrote down all of our major concerns (the major factors) about the suitability of a lot for our home. Then we ranked the concerns. It turned out that landscaping was far down on the list, so we reevaluated the lots we had excluded and moved a couple of them to the top of our list.
There are three inherent weaknesses in our instinctive method. First, we tend to apply different criteria to the different items being ranked. Second, we tend to regard all of our criteria as having equal importance to us, when one can easily demonstrate (as in my experience in North Carolina) that this is not the case. Third, we don’t rank every item individually against every other item.
For these reasons, rankings generated with our instinctive method tend to be inconsistent and are thus unreliable. But the degree of error (the extent to which the rankings are out of order) is rarely a problem for us, because most of the things we rank, such as the clothes we wear, the route we drive to work, or the movies listed above, are of a mundane, commonplace nature. But when the decisions we make in ranking are crucial, as in, say, selecting one of several lawyers to represent us or our company in a damage suit or choosing among sites for building a home or a multimillion-dollar office complex, our instinctive method poses hazardous pitfalls.
“But,” you say, “when I rank really important things, things in which I have a vital stake, I don’t use the method I did to rank the movies. I’m more careful and systematic. I use a different, more reliable method.”
I seriously doubt it. If you are like most members of our species —and I include myself in that number—your mind doesn’t distinguish between vital and nonvital matters when it comes to ranking. We tend in every case to use our instinctive method—the one we’re born with, the one we’ve used all our lives.
But we shouldn’t! When we have a great deal invested personally or corporately in the results of a ranking, we should employ an unwaveringly consistent method whose results we can rely upon unconditionally. The only way I know to ensure reliable results is to impose a systematic structure on the process. But how do we do that? What systematic technique will enable us to determine which criteria are the most important and apply them equitably to all the items being ranked? The answer is a technique called “weighted ranking.”
The paramount feature of weighted ranking is its method of ranking each item against every other. It’s very simple. It’s called “pair ranking.” Here’s how it works.
Let’s say we are ranking four options: A, B, C, and D. To pair-rank these options, we list them in a column one beneath the other:
Option A
Option B
Option C
Option D
We then ask ourselves:
Which is better, A or B? We put a pencil mark after the one we decide is better, say, B.
Option A
Option B |
Option C
Option D
We then ask why B is better and record our reasoning separately. If we don’t ask why we favor B over A, the voting yields only our preference, not our rationale. Yet identifying the rationale is the most important part of the process.
Which is better, A or C? We put a pencil mark after, say, C, and record our reasoning.
Option B
| Option C
| Option D
Which is better, A or D? We put a mark after, say, D, and record our reasoning.
Option A
Option B |
Option C |
Option D |
Which is better, B or C? We mark B and record our reasoning.
Option A
Option B ‖
Option C |
Option D |
Which is better, B or D? We mark B and record our reasoning.
Option A
Option B‖|
Option C |
Option D |
Which is better, C or D? We mark C and record our reasoning.
Option A
Option B ‖|
Option C ‖
Option D |
We thus systematically compare each item with every other item. If we have been consistent in our rankings, one of the items will have three marks (votes), one will have two, one will have one, and one will have none. The item with three votes is the most favored and thus is ranked first. The item with two is second; one vote—third; no votes—fourth. If, by chance, two items end up with the same number of votes because our analysis was inconsistent, we simply rank these two items head to head to break the tie. The benefits of pair ranking aren’t noticeable with short lists of four or five items, but with longer lists they are unmistakable.
So let’s try it. Pair-rank your list of fifteen movies and enter your rankings in the next column of the Ranking Techniques Matrix and label that column “Pair Ranking.”
BEFORE CONTINUING, PAIR-RANK THE MOVIES, ENTER YOUR PAIR RANKINGS IN THE RANKING TECHNIQUES MATRIX, AND LABEL THE COLUMN “PAIR RANKING.”
See my pair rankings in Figure 10-2.
You may feel uncomfortable with pair ranking and think that it’s too mechanical and laborious. Well, your discomfort is only natural. It’s a manifestation of your mind sending you signals telling you, “I don’t like to work this way. I prefer my loosey-goosey, unfettered, mental-messing-around instinctive approach.” Ignore these signals. What’s happening here is that we’re running against the mind’s grain, against the way it prefers to operate, so of course it feels uncomfortable. Once it becomes accustomed to pair ranking, it will feel at home with the technique and won’t want to rank things any other way. And neither will you.
But is it really “mechanical and laborious”? Mechanical, yes. That’s its beauty. It’s systematic: 1 against 2, 1 against 3, 1 against 4, 2 against 3, 2 against 4, 3 against 4. But is it “laborious”? Yes again. One has to methodically, over and over again, reason out each pair to be ranked. But that’s what makes pair ranking so valuable analytically. It doesn’t permit us to take analytic shortcuts that shortchange our analysis. We must analyze and make a decision on each member of every pair.
FIGURE 10-2
Pair ranking, by comparing one thing against another, conforms to the one-track, ever-focusing nature of our minds. It narrows the mind’s field of attention first to a single pair and then separately to each of the items in the pair. Ranking things in pairs is something the mind can do easily, quickly, and effectively. The mind does love to focus.
Pair ranking offers a simple, reliable way to rank items, regardless of the subject matter. By focusing on individual items, pair ranking separates the elements of the task—the problem—in an organized way that, like all effective structuring techniques, allows us to analyze each element separately, systematically, and sufficiently. Pair ranking also provides reliability. By measuring every item against every other, it provides an absolutely reliable indicator of where each item ranks. What happens is that the process delivers the rankings. We don’t have to decide which movie is fifth and which is sixth or which is eleventh and which is twelfth. Instead, we rank them in pairs and the process puts them into order. With instinctive ranking we can only guess whether each item being ranked is in its proper place. With pair ranking we are certain.
Now, take a look at the Ranking Techniques Matrix and compare the results of your instinctive ranking with the results of your pair ranking. Do you note any differences? Twelve of my rankings changed by an average of nearly four places. Two movies moved five places, and one (Star Wars) went from thirteenth to fifth.
Having learned what pair ranking is all about, we are now ready to review the nine steps of weighted ranking, still using movies as our working example.
Step 1: List all of the major criteria for ranking.
Write down in a column on a sheet of paper eight criteria for ranking movies, for example, type of plot, strength of plot, degree of excitement, level of violence, cinematography, music, the cast, the director, whether a film has won an Oscar, and so on.
BEFORE CONTINUING, WRITE DOWN EIGHT CRITERIA FOR RANKING MOVIES.
Step 2: Pair-rank the criteria.
We now must determine which of these criteria is the most important. To do that we simply pair-rank them: the first against the second, first against the third, and so on. Add up the votes you give to each criterion. The one with the most votes is the top criterion, the one with the second most votes is second, and so on.
As you practice pair ranking, you’ll discover that sometimes you can quickly determine with certainty which item is going to be first or which last. When you do, make a note of it and don’t include that item anymore as you rank the others.
BEFORE CONTINUING, PAIR-RANK THE CRITERIA.
Figure 10-3 shows my pair ranking of eight criteria.
Step 3: Select the top several criteria and weight them in percentiles (their sum must equal 1.0).
For this exercise alone, use only your top three criteria. Of course, when you apply this structuring technique to your own business or personal problems, you can employ as many criteria as you wish.
FIGURE 10-3
Weight your three criteria by dividing 100 points among them according to the importance you assign to each. Convert these points to percentiles; their total must equal 1.0.
Figure 10-4 shows my weightings of my top three criteria.
FIGURE 10-4
For me, “strength of plot” is significantly more important than “type of plot” and more than twice as important as “cast.”
BEFORE CONTINUING, ASSIGN PERCENTILE WEIGHTS TO YOUR TOP THREE CRITERIA.
Step 4: Construct a Weighted Ranking Matrix and enter the items to be ranked, the selected criteria, and the criteria weights.
Use the matrix in Figure 10-5 as a guide.
BEFORE CONTINUING, CONSTRUCT A WEIGHTED RANKING MATRIX AND ENTER YOUR FIFTEEN MOVIES AND YOUR TOP THREE CRITERIA AND THEIR WEIGHTS.
FIGURE 10-5
Figure 10-6 shows my Weighted Ranking Matrix, the movies to be ranked, my three criteria, and their weights.
Step 5: Pair-rank all of the items by each criterion, recording in the appropriate spaces the number of “votes” each item receives.
At this juncture, the technique gets a bit more complicated, but there’s no way around it if we are to rank all options equitably. What we’re going to do is pair-rank the movies by each of three criteria, which means performing three separate rankings.
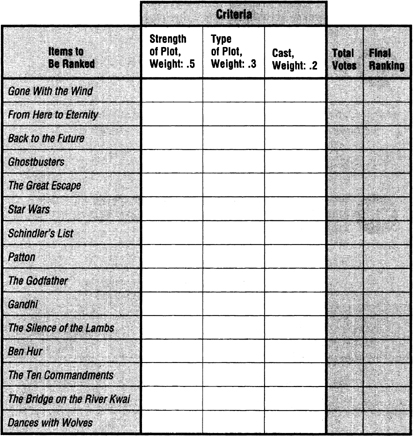
FIGURE 10-6
If you feel a panic attack coming on, remember it’s only your subconscious screaming, I don’t like this! I don’t analyze this way!” Don’t listen to it. Just stick with me. This technique, once you understand it, is really quite simple.
Rank the fifteen movies by the first criterion and enter the number of votes each movie receives. Repeat the same process for the second and third criteria. See my example in Figure 10-7.
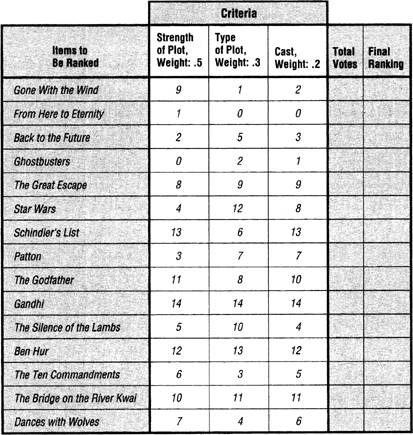
FIGURE 10-7
BEFORE CONTINUING, RANK THE MOVIES BY EACH CRITERION AND ENTER THE NUMBER OF VOTES.
Step 6: Multiply the number of votes by the respective criterion’s weight.
Multiply the number of votes for each entry under each criterion by that criterion’s weight. See how I did it in Figure 10-8.
FIGURE 10-8
BEFORE CONTINUING, MULTIPLY THE NUMBER OF VOTES BY CRITERION WEIGHTS.
Step 7: Add the weighted values for each item and enter the sums in the column labeled “Total Votes.”
Add up the number of votes each movie receives under all three criteria and enter the sums under “Total Votes.” See how I did it in Figure 10-9.
FIGURE 10-9
BEFORE CONTINUING, ADD WEIGHTED VALUES AND ENTER SUMS UNDER “TOTAL VOTES.”
Step 8: Determine the final rankings and enter them in the last column, labeled “Final Ranking.” (The item with the most points is ranked highest.)
The movie with the highest number of votes is ranked first, second highest second, and so on (Figure 10-10).
FIGURE 10-10
BEFORE CONTINUING, ENTER FINAL RANKINGS.
Step 9: Perform a sanity check.
Do the results make intuitive sense? If not, go back and check the rankings, the weights, and the arithmetic. Don’t be surprised if the results are discomforting. Our instinctive ranking approach still drives our intuition, so we may feel uncomfortable with the results of weighted ranking.
Now copy the final rankings into the last column of the Ranking Techniques Matrix, and label that column “Weighted Ranking,” as in Figure 10-11. The Ranking Techniques Matrix reveals rather impressively how the positions of the movies shift as the technique becomes more definitive and thus more reliable as we incorporate first pair ranking and finally weighted ranking. Compare the positions under “Instinctive Ranking” and “Weighted Ranking.” How significant were the changes? Gandhi remained my top choice, but Gone With the Wind (instinctively second) dropped to tenth, while Ben Hur (instinctively eighth) moved up to second.
You may argue that these changes in rankings between the two techniques are only superficial; that is, they show only that weighted ranking results in a different order than instinctive ranking. Indeed, my rankings of some of the movies changed very little or not at all. For example, Gandhi was my top-ranked movie in both the instinctive and weighted rankings. So what did weighted ranking buy me over instinctive ranking? I got the same result: Gandhi was number one.
The answer is confidence in the validity of the rankings. What if we really had a vital interest in how these movies were ranked? What if millions of dollars were at stake? In that case, the validity of the rankings would be critical, and validity is what weighted ranking ensures.
How can one place any trust in the results of instinctive ranking, which is inherently flawed? It is an unsystematic approach that is flagrantly vulnerable to our fallible reasoning traits and that applies criteria inconsistently, without giving equal consideration to each item being ranked. In short, instinctive ranking is a disaster waiting to happen.
FIGURE 10-11
Therefore, at a minimum, always use pair ranking. Pair ranking is reliable and so easy that a child can do it. But if you are faced with a situation in which ranking is important, you would be well advised to employ weighted ranking—an unwaveringly consistent method on whose results we can rely unconditionally.
As with anything in life, if you practice the weighted ranking technique, you will gain confidence in using it, and what at first seems foreign, awkward, and unwieldy will become second nature. Practice, practice, practice. What more can I say? I promise you won’t regret it.
As a prelude to purchasing a new car, we are going to rank ten different makes and models. I’ll walk you through the steps, working the problem myself as we go.
Step 1: List all of the major criteria for ranking.
I list all the criteria I think might be important, combining those that are similar. My criteria are as follows: price, mileage, reliability, ease of driving, attractiveness of styling, safety record, insurance cost, fuel tank capacity, luggage compartment capacity, engine horsepower, and turning radius.
Step 2: Pair-rank the criteria.
I pair-rank the criteria, comparing the first in the list against the second, against the third, and so on. I then count the votes each criterion received and write that number adjacent to the criterion. Figure 10-12 shows the results of my pair rankings.
How, you may ask, can I be certain that I have ranked every item against every other item in the list? It’s actually quite easy. Use the following formula: multiply N (where N equals the number of items in the list) by N minus 1 (the number of items less one) and divided by two.
This formula will give you the total number of votes that would be assigned to all of the items if every item were ranked against ever other item. If, when you add up all of the votes, the sum does not equal the formula’s total, you have made an error in pair ranking and should repeat the pair-ranking step.
Step 3: Select the top several criteria and weight them in percentiles (their sum must equal 1.0).
FIGURE 10-12
Price, attractiveness, and reliability are my top three criteria, which I weight as .5, .3, and .2 respectively.
Step 4: Construct a Weighted Ranking Matrix and enter the items to be ranked, the selected criteria, and the criteria weights.
I construct the matrix in Figure 10-13.
Step 5: Pair-rank all of the items by each criterion, recording in the appropriate spaces the number of “votes” each item receives.
Figure 10-14 shows my pair rankings.
Step 6: Multiply the votes by the respective criterion’s weight.
Figure 10-15 shows my weighted votes.
FIGURE 10-13
Step 7: Add the weighted values for each item and enter the sums in the column labeled “Total Votes.”
Figure 10-16 shows my total weighted votes.
Step 8: Determine the final rankings and enter them in the last column, labeled “Final Ranking.” (The option with the most points is ranked highest.)
FIGURE 10-14
Figure 10-17 shows my final rankings. My analysis indicates that, according to my preferences, Saturn is my first choice and Chevrolet Geo Prizm a close second.
Step 9: Perform a sanity check.
I am intuitively comfortable with this finding.
FIGURE 10-15
The process of making personnel decisions is usually driven by highly subjective mind-sets, uneven and inequitable consideration of personal qualifications (usually based on formal performance evaluations), and, worst of all, slipshod adherence to standards (criteria) of performance. Because the weighted ranking technique goes a long way toward eliminating these undesirable influences, it is ideally suited for analyzing personnel decisions such as choosing among applicants for hiring, selecting among candidates for advancement to a more senior position, and so on.
FIGURE 10-16
Consider, for example, how weighted ranking can be used for ranking employees for promotion — a standard, prevalent, and ever-contentious function of management. To illustrate the technique’s effectiveness in this application, I will use four (out of ten) criteria to rank ten salespeople being considered for promotion to the position of regional sales manager in a hypothetical manufacturing company.
FIGURE 10-17
Step 1: List all of the major criteria for ranking.
I will stipulate, for the purpose of this demonstration, the following ten criteria for promotion: the candidate’s supervisory experience, knowledge of the company’s products, salesmanship, communication skills (speaking and writing), budget management, creativity (in all aspects of responsibility), dedication, image (of the candidate as seen by employees and management alike), personal integrity, and earnings for the company through sales.
Step 2: Pair-rank the criteria.
Figure 10-18 shows my pair ranking of the criteria.
Step 3: Select the top several criteria and weight them in percentiles (their sum must equal 1.0).
Product knowledge, communication skills, image, and budget management are my four criteria, which I weight as .4, .3, .2, and .1 respectively.
Step 4: Construct a Weighted Ranking Matrix and enter the items to be ranked, the selected criteria, and the criteria weights.
FIGURE 10-18
I construct the matrix in Figure 10-19.
Step 5: Pair-rank all of the items by each criterion, recording in the appropriate spaces the number of “votes” each item receives.
Figure 10-20 shows the votes each item received from my pair rankings by each criterion.
Step 6: Multiply the votes by the respective criterion’s weight.
Figure 10-21 shows the weighted votes.
Step 7: Add the weighted values for each option and enter the sums in the column headed “Total Votes.”
Figure 10-22 shows the total weighted votes for each item.
FIGURE 10-19
FIGURE 10-20
Step 8: Determine the final rankings and enter them in the last column, headed “Final Ranking.” (The option with the most points is ranked highest.)
Figure 10-23 shows the final rankings. This analysis indicates that Susan should be my first choice, edging out Cynthia by a slim margin. However, because the top four rankings are very close, ranging from 6.7 to 7.3, it would pay to repeat the ranking process with just those four individuals, as in a runoff election—just to be sure. There’s a lot riding on this analysis, and I want to be fair as well as accurate in my judgments.
Step 9; Perform a sanity check.
Here, for your review and reference, are the nine steps of weighted ranking:
FIGURE 10-21
Step 1: List all of the major criteria for ranking.
Step 2: Pair-rank the criteria.
Step 3: Select the top several criteria and weight them in percentiles (their sum must equal 1.0).
Step 4: Construct a Weighted Ranking Matrix (see Figure 10-24) and enter the items to be ranked, the selected criteria, and the criteria weights.
Step 5: Pair-rank all of the items by each criterion, recording in the appropriate spaces the number of “votes” each item receives.
Step 6: Multiply the votes by the respective criterion’s weight.
Step 7: Add the weighted votes for each item and enter the sums in the column headed “Total Votes.”
FIGURE 10-22
Step 8: Determine the final rankings and enter them in the last column, headed “Final Ranking.” The item with the most votes is ranked highest.
Step 9: Perform a sanity check.
Using the above steps as a guide, practice the weighted ranking technique on the following two problems.
You are planning to take a client to dinner this evening with several of your business associates and wish to make a good impression on him. Because you have never met him before, you are uncertain about his tastes in cuisine and dining atmosphere. But there has been no time to find out. He is arriving by plane in a matter of hours, and a dinner reservation must be made now. Think of five restaurants of different cuisine that you have patronized and that you believe would impress such a visitor. Based entirely on your own experience and preferences, rank the five restaurants based on the following four criteria: price of food, quality of food (meaning appearance and taste), quality of service, and the degree to which the general atmosphere in the restaurant adds to the pleasure of the meal.
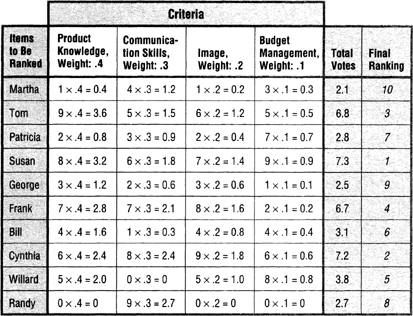
FIGURE 10-23
BEFORE CONTINUING, COMPLETE THE RESTAURANTS PROBLEM.
The solution to Exercise 25 (page 333) shows the matrix you should have constructed.
FIGURE 10-24
Using the weighted ranking technique, determine which of the following famous business magnates is the most inspiring role model for young people interested in business careers: Ross Perot, Donald Trump, Lee lacocca (Ford and Chrysler), Bill Gates (Microsoft), and Michael Eisner (Disney).
Here are eight criteria for your consideration in Step 1: innovative projects that they managed or in which they were involved, business accomplishments, philanthropic activities, moral standards, political activities, importance of their business activities to the nation’s welfare, public image of the corporations they have headed, and personal life (as portrayed in the news media).
Please add other criteria you believe would be relevant and eliminate any criteria on which you lack sufficient knowledge. Remember, this is just an exercise; there is no right or wrong answer. In Step 3, in this exercise only, select only the top three criteria.
BEFORE CONTINUING, COMPLETE THE BUSINESS MAGNATES PROBLEM.
The solution to Exercise 26 (page 333) shows the matrix you should have constructed.
If the results of a weighted ranking are absolutely critical to some decision, you may wish to obtain a more precise ranking by inserting an additional procedure after Step 5. Step 5 determines the votes each item receives by pair ranking under each criterion. But these rankings assume that the degree of preference reflected in the votes is evenly divided among all of the items.
For example, let’s say we are ranking four home appliances—vacuum cleaner, lawn mower, hair dryer, and power handsaw—according to the criterion of Ease of Use. In Step 5, vacuum cleaner receives 2 votes, lawn mower 0, hair dryer 3, and power handsaw 1. Thus, hair dryer is 1st, vacuum cleaner 2nd, power handsaw 3rd, and lawn mower 4th. Without further analysis we would be forced to assume that under this criterion vacuum cleaner is three-fourths as preferred as hair dryer, power handsaw one-half as preferred, and lawn mower one-fourth as preferred. Yet the votes from the pair ranking tell us only the order of ranking, not the degree of preference for each item. We can determine degree of preference only by subjectively stipulating it.
There are basically three ways of assigning degree of preference. All three begin by replacing the votes from Step 5 with the numerical ranking of the items under each criterion. For example, let’s assume we have just completed Step 5 in ranking the four household appliances by the Ease of Use criterion. Beside (or in place of) the votes for each item we insert the ranking commensurate with those votes (see Figure 10-25).
The first and simplest way to assign preferences is, as a new Step 5A, to divide one hundred points among the items. These points replace the rankings. In the case of our four appliances, let’s say we assign 60 points to hair dryer, 20 to vacuum cleaner, 15 to power handsaw, and 5 to lawn mower (see Figure 10-26).
FIGURE 10-25
This distribution of points means that hair dryer is 3 times more preferred than vacuum cleaner, 4 times more preferred than power handsaw, and 12 times more preferred than lawn mower. We then continue with the other steps, multiplying the points by the weight of their respective criterion, adding up the points for each appliance, and determining the final rankings. The item with the most weighted points is ranked highest.
The second way, a variant of the first, is to gauge the relative preference of each item visually, using columns drawn on graph paper (see Figure 10-27). We first draw a column for the highest ranked item, which in this example we label Hair Dryer. We then draw columns for the other three appliances in the order of their respective rankings and label them Vacuum Cleaner, Power Handsaw, and Lawn Mower. We make the heights of these columns visually proportionate to the degree of preference we subjectively assign to each appliance in comparison to the Hair Dryer column.
We then determine the height of each column using the cells of the graph paper as the scale. Let’s say the height of the Hair Dryer column is 50 cells, the Vacuum Cleaner column is 35 cells, Power Handsaw 20, and Lawn Mower 10. We enter these values into the weighted-ranking matrix under the Ease of Use criterion. We then follow through with the other steps and determine the final rankings. As long as the scale on the graph paper used to measure the height of the columns is uniform, it makes no difference what the height is of the first column against which the others are proportioned. The final rankings will be reliable.
FIGURE 10-26
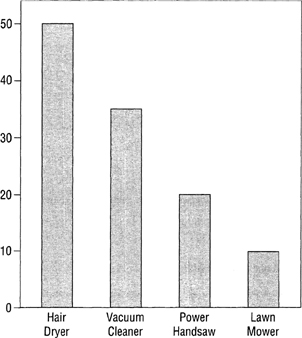
FIGURE 10-27
The third way to assign degree of preference is algebraic and again involves distributing 100 points. In this method we assign a decimal fraction of Hair Dryer to each of the other appliances. We represent Hair Dryer as X. Thus, we might view Vacuum Cleaner as being .3 (about one-third) of the preference we assign to Hair Dryer, i.e., Vacuum Cleaner = .3X. Continuing, Power Handsaw = .25X and Lawn Mower .IX. If we assume that the X values of the four appliances together equal 100 points, then we can formulate the following algebraic equation and solve for X:
X+.3X+.25X+.1X=100
1.65X= 100
X (Hair Dryer) = 61
In which case,
Vacuum Cleaner = .3 times 61 = 18
Power Handsaw = .25 times 61 = 15
Lawn Mower = .1 times 61 = 6
Again, we enter these values into the matrix and calculate the final rankings.
Two effective ways of dealing with a large number of items to be ranked are as follows:
Working down the list of items, mark beside each an H, M, or L for High, Medium, or Low ranking. You will find it comparatively easy and quick to assign these rankings, but when in doubt, assign the higher rank. This initial rough categorization separates the list into three groups. If we are interested in only the best item in all three groups, we apply the weighted ranking technique to only the High Group. If we wish to select, say, the top ten items, but the High Group contains only nine, we rank the Medium Group using weighted ranking, move its best item into the High Group, and rank the High Group using weighted ranking.
Alternatively, with a smaller number of items, we can separate the list into just two groups—High and Low—and work on from there.
This approach is used when a group of people is doing the ranking. Each member of the group selects the best five items from the list. These best fives are consolidated into a single list, which the group, working together by voting or consensus, then pair ranks. The number of items each member initially selects can, of course, be varied, depending on the total number of items on the list and the number ultimately desired by the group.
* You thought the director was a “he,” didn’t you! It’s those bothersome mental traits again.
