CHAPTER 6
St. Augustine Numbers
St. Augustine declared he had seen acephalic creatures, with eyes in their breasts.…
—Glasgow Herald, December, 31, 1924
Love with care—and then what you will, do.
—St. Augustine
|
CHAPTER 6
St. Augustine declared he had seen acephalic creatures, with eyes in their breasts.… —Glasgow Herald, December, 31, 1924 Love with care—and then what you will, do. —St. Augustine |
“Mr. Plex, I’m starting to worry.” You gaze up at the statue of Aphrodite. Her left index finger is now several feet long and starting to puncture a nearby centaur’s carotid artery. Strewn haphazardly beneath Aphrodite’s feet are the discarded remains of coffee cups, french fry bags, and an occasional hamburger bun.
“Sir, I’ll try to find a broom and sweep out our backroom.”
“I’m not referring to the trash, you fool. It’s the statues. I —I’ve a feeling our presence in the past is interfering with history.”
“We’re subtly changing the past?”
You nod. “Let’s start packing our things this week.” You motion to some notebook computers, the view-screen, a box of electronic flies.…
Mr. Plex nods.
You sit down beneath Aphrodite. “Mr. Plex, while Pythagoras is cleaning his own house, I’ve something interesting to show you. Our agents discovered it in St. Augustine’s time, A.D. 390, in Africa.”
Mr. Plex comes closer and stares intently at you. You hand him a paper with the number “153” on it.
“St. Augustine, the famous Christian theologian, thought 153 was a mystical number, and that 153 saints would rise from the dead in the eschaton.”
Mr. Plex rubs his forelimbs together. “How is that?” 83
“St. Augustine interpreted the Bible using numbers. For example, he was fascinated by a New Testament event (John 21:11) where the apostles caught 153 fish from the sea of Tiberias. Seven disciples hauled in the fish using nets. St. Augustine reasoned that these seven were saints.”
“Sir, how could he know that?”
“Since there are seven gifts from the Holy Ghost which enable men to obey the ten commandments, he thought the disciples must therefore be saints. Moreover, 10 + 7 = 17, and if we add together the numbers 1 through 17, we get a total of 153.” You pause. “The hidden meaning of all this is that 153 saints will rise from the dead after the world has come to an end.”
“It makes you wonder.” Mr. Plex pauses and grins revealing his diamond teeth. “153 is my favorite integer.”
“And why is that?”
“Because 153 = 1! + 2! + 3! + 4! + 5!, where the ‘!’ symbol means factorial. (Factorial is the product of all the positive integers from one to a given number. For example, 5! = 1 × 2 × 3 × 4 × 5 = 120.)”
“Excellent, Mr. Plex, but better than that, 153 =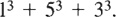 
Are there any other 3-digit numbers that equal the sum of the cubes of their own digits?”
“Mon Dieu! Here’s something new.” Mr. Plex pauses. “When the cubes of the digits of any 3-digit number which is a multiple of 3 are added, and the digits of the resulting number are cubed and added, and the process continued, the final result is 153. For instance, start with 369, and you get the sequence: 369, 972, 1080, 513, 153.” Mr. Plex’s limbs are shaking like a buzzsaw. “Could St. Augustine have known anything about this?”
“Curiouser and curiouser, Mr. Plex.” You pause. “153 is also the 17th triangular number, and I just told you why St. Augustine thought 17 is important. It’s the sum of 10 (for the ten commandments of the Old Testament) and 7 (for the gifts of the Spirit in the New Testament).”
“Back to triangular numbers again! Pythagoras would have liked all this. What could this all mean?”
“Just interesting coincidences, I’m sure.”
Just then there is a knock on the door to your backroom hideout.
Mr. Plex goes over to the door. “Who’s there?”
You try to pull him back from the door. “Shut up you fool.”
A woman’s voice comes from the other side of the door. “It’s me, Theano.”
Your heartbeat quickens as you walk over to the door and pull it open.
Theano hesitantly enters. From her ears dangle golden earrings in the shape of the tetraktys—the Pythagorean symbol consisting of 10 dots forming a triangle. Inscribed on her golden bracelets are various triangular and oblong numbers.
She holds herself like a queen. Her long neck curves like a bird taking wing. “I couldn’t help coming back,” she says while gazing into your eyes. “I want to learn.”
At the husky tone of her voice, you shiver imperceptibly and all the air is expelled from your lungs in one wild gasp.
A fire within her seems to shoot upward and outward. “I want to learn.”
St. Augustine really was interested and excited about the number 153. St. Aurelius Augustinus Augustine was born in the year 354 and became the bishop of Hippo in Africa from A.D. 396–430. His mother, Monica, was Christian since girlhood. His father, Patricius, became Christian later in life.
St. Augustine’s life was not always what normally associates with a saint. As a teenager, he became the unwed father of a boy he named Adeodatus. His mother was determined to find Augustine a proper marriage partner and get him married. She eventually found a “suitable” bride, who was not quite of marriageable age, and dismissed Adeodatus’ mother, Augustine’s true love. The whole incident distressed Augustine who proclaimed, “Give me chastity, but not yet!” Instead of marrying immediately, he found another girlfriend. (This chronology is not meant to disparage St. Augustine who was also a brilliant and spiritual man.)
Interestingly, St. Augustine’s method of combining two influences (10 + 7 = 17) had its roots with the Pythagoreans. Recall how Pythagoras associated 5 with marriage because 5 = 2 (female) + 3 (male).
English mathematician Godfrey Hardy (1877–1947), in his book A Mathematician’s Apology, gives 153 = 13 + 53 + 33 as an example of a rare number which is the sum of the cubes of its digits. However he does not ascribe any mystical or mathematical profundity to this. In fact, he comments,
These are odd facts, very suitable for puzzle columns and likely to amuse amateurs, but there is nothing in them that appeals to the mathematician. The proofs are neither difficult nor interesting—merely a little tiresome.
St. Augustine numbers, which are the sums of cubes of their digits, are a subset of a large class of numbers, which are the sums of powers of their digits. In other words, there are other n-digit numbers which are equal to the sum of the nth powers of their digits. Variously called narcissistic numbers, “numbers in love with themselves,” Armstrong numbers, or perfect digital variants, these numbers have fascinated number theorists for decades. (The Appendix includes BASIC program code for computing St. Augustine numbers.)
The largest narcissistic number discovered to date is the incredible 39-digit number:
115132219018763992565095597973971522401
(Each digit is raised to the 39th power.) Can you beat the world record? What would Pythagoras have thought of this multidigit monstrosity?
As one searches for larger and larger narcissistic numbers, will they eventually run out? If they are proven to die out in one number system, does this mean they are finite in another? Martin Gardner wrote to me recently indicating that the number of narcissistic numbers has been proved finite. They can’t have more than 58 digits in our standard base 10 number system.
Modern writer W. E. Bowman uses the number 153 throughout his book The Ascent of Rum Doodle. For example, there are 153 porters hired for a train which ascends the Himalayan mountains. The number 153 is also associated with the depth of a crevasse, the speed of the train, and the height of a ship above sea level.
I have not determined whether Bowman uses 153 because he is aware of St. Augustine’s prediction regarding 153 saints rising from the dead when the world comes to an end.
There really was an important woman named Theano in ancient Greece. If you have not already guessed her identity, you will in the next chapter.