
|
The God of the Old Testament is a God of power, the God of the New Testament is a God of love; but the God of the theologians, from Aristotle to Calvin, is one whose appeal is intellectual: His existence solves certain puzzles which otherwise would create argumentative difficulties in the understanding of the universe,
—Bertrand Russell, A History of Western Philosophy |
It is in a way a forlorn and perhaps even hopeless objective—to demonstrate the existence of God by numerical coincidences to an uninterested, to say nothing of a mathematically unenlightened public.
—Carl Sagan, Broca’s Brain
Euler strode up to Diderot and proclaimed: “Monsieur, (a + bn)/n = X, donc Dieu existe!” [”Sir (a + bn)/n = X, therefore God exists!”]
—Michael Guillen, Bridges to Infinity
The cave is bright in the morning light. A few drops of cool liquid fall from a stalactite onto your outstretched palm. You turn toward Theano and Mr. Plex who are sitting with their backs against the cave wall.
“Today, I want to tell you about the use of computers, mathematics, and logic to prove the existence of God.”
Mr. Plex’s eyes seem to light up like little lanterns. “Is that possible, Sir?”
“Many have tried. Several 20th-century proofs involved mathematics, but some of the most famous proofs of God’s existence started with Saint Thomas Aquinas. He lived from 1225 to 1274 and gave five proofs of God’s existence in his Summa Theologica. The flavor of many of his arguments is as follows. In this universe, there are things which are only moved, and other things which both move and are moved. Whatever is moved is moved by something, and since an endless regress is impossible, we must arrive somewhere at something which moves without being moved. This unmoved mover is God.”
Mr. Plex scratches his head. “Not very persuasive.” God’s
You nod. “While this argument may not seem very persuasive today, during Aquinas’ time it caused quite a stir. Interestingly, Aquinas loved to make lists of things which God cannot do. He cannot be a body or change Himself. He cannot fail. He cannot forget or grow tired, or repent or be angry or sad. He cannot make a man without a soul or make the sum of the angles of a triangle less than 180 degrees. He cannot make another God, cannot kill Himself, and cannot undo the past or commit sins.”
Mr. Plex shifts his position against the cave wall as a drop of clear water falls upon his forelimb. “Sir, what about Aristotle?”
“Both Aquinas and Aristotle didn’t like an infinite regression of causes, and they used their dislike to demonstrate God’s existence. But these great minds lived before infinite mathematical series were commonplace concepts. How would the history of religion have changed if Aristotle and Aquinas knew integral calculus and infinite sequences? Would Aquinas have been better prepared to conceive of an infinitely old universe requiring no creator?” You pause. “Carl Sagan, a great 20th-century science popularizer, often talked about Aquinas’ and Aristotle’s unmoved mover God. I recall from Sagan’s book Broca’s Brain, ‘As we learn more and more about the universe, there seems less and less for God to do. Aristotle’s view was of God as an unmoved prime mover, a do-nothing king who establishes the universe and then sits back and watches the intertwined chains of causality course down through the ages.’ ”
Theano is stirring a pool of water with her finger. The ripples make faint splashing sounds as they contact a central stalagmite. She looks at you. “Sounds like lots of people have tried to prove God’s existence using mathematical proofs, but has anyone tried to disprove the existence of God?”
“Yes. The early Christian writer Lucius Lactantius quotes the Greek atheist Epicurus in The Anger of God:
God either wishes to take away evil, and is unable, or He is able, and is unwilling; or He is neither willing nor able, or He is both willing and able. If He is willing and is unable, He is feeble, which is not in accordance with the character of God. If He is able and unwilling, He is envious, which is equally at variance with God. If He is neither willing nor able, He is both envious and feeble, and therefore not God. If He is both willing and able, which alone is suitable to God, from what source then is evil? Or why does He not remove evil?
The wind grows stronger near the mouth of the cave, and the blue of the sky outside the cave was fast turning to beige. The dwindling light tinged the cave the color of salmon. Occasionally, you hear strange animal cries and the sounds of insects. You look at Theano who appears to have a slight shiver.
“I’m OK,” she says.
You continue. “In one of his more skeptical moods, St. Thomas Aquinas wrote in Summa Theologica:
It seems that God does not exist; because if one of two contraries be infinite, the other would be altogether destroyed. But the name God means that He is infinite goodness. If, therefore, God existed there would be no evil discoverable; but there is evil in the world. Therefore God does not exist. Further, it is superfluous to suppose that what can be accounted for by a few principles has been produced by many. But it seems that everything we see in the world can be accounted for by other principles, supposing God did not exist. For all natural things can be reduced to one principle, which is human reason, or will. Therefore there is no need to suppose God’s existence.
Theano stares intently at you. “What do you think? Can mathematics be used to prove God exists?”
“I don’t believe that mathematical ‘proofs’ can be used to prove or disprove the existence of God, but ever since the time of Pythagoras, philosophers have attempted just this. Each philosopher in turn has found fault with his predecessor: Saint Thomas rejected Saint Anselm’s proofs, and Kant rejected Descartes …”
“Sir, what about some more recent examples?” says Mr. Plex.
“Perhaps the most interesting example of a mathematician studying cosmic questions is Austrian mathematician Kurt Goedel who lived from 1906 to 1978. Sometime in 1970, Goedel’s mathematical proof of the existence of God began to circulate among his colleagues. The proof was less than a page long and caused quite a stir. Also, a German mathematician Georg Cantor, who lived from 1845 to 1918, was interested in the way mathematics may imply the existence of God. In letters to Cardinal Franzelin, Cantor explicitly indicated that the infinite, or Absolute, belonged uniquely to God. Cantor developed a mathematical theory of different levels of infinity inhabited by transfinite numbers. These are infinite numbers, which we symbolize by the Hebrew letter aleph.” You draw the X symbol on the cave floor. “These numbers are used today in mathematics dealing with sets of numbers. For example, the smallest transfinite number is called ‘aleph-nought.’ ” You sketch K0 on the cave floor. “This number counts the number of integers. There are even larger infinities, such as the number of irrational numbers like the square root of 2 which cannot be expressed as a fraction. Cantor believed that God ensured the existence of these transfinite numbers. Cantor regarded the transfinite numbers as leading directly to the Absolute, to the one ‘true infinity’ whose magnitude was capable of neither increase nor decrease but could only be described as an absolute maximum that was incomprehensible within the bounds of human understanding. The absolute infinite was beyond determination, since once determined, the Absolute could no longer be regarded as infinite, but was necessarily finite by definition.”
Theano jumps back from the pool of water. “What are those?”
You come closer, and see numerous flesh-colored objects moving in the pool. “Ah, just some blind cave fish. Amazing how they evolved to function so well without eyes. Their non-visual senses must be very acute to compensate for lack of vision.”
Mr. Plex looks at the fish, and then taps you on the shoulder. “Sir, what did Cantor’s colleagues think about his ideas on God and infinity?”
“Good question, Mr. Plex. Constantin Gutberlet, one of Cantor’s contemporaries, worried that Cantor’s work with mathematical infinity challenged the unique, ‘absolute infinity’ of God’s existence. However, Cantor assured Gutberlet that instead of diminishing the extent of God’s dominion, the transfinite numbers actually made it greater. After talking to Gutberlet, Cantor became even more interested in the theological aspects of his own theory on transfinite numbers.”
Theano looks up from the pool of blind cave fish. “Seems like Gutberlet should like Cantor’s ideas because they make God’s universe all the more impressive.”
“Right. Gutberlet subsequently made use of Cantor’s ideas and claimed God ensured the existence of Cantor’s transfinite numbers. God also ensured the ideal existence of: infinite decimals, the irrational numbers, and the exact value of π. Gutberlet also believed that God was capable of resolving various paradoxes which seem to arise in mathematics. Furthermore, Gutberlert argued that since the mind of God was unchanging, then the collection of divine thoughts must comprise an absolute, infinite, complete closed set. Gutberlet offered this as direct evidence for the reality of concepts like Cantor’s transfinite numbers.”
You turn your attention from the fish to Mr. Plex and Theano. “Cantor’s own religiosity grew as a result of his contact with various Catholic theologians. In 1884, Cantor wrote to Swedish mathematician Gösta Mittag-Leffler explaining that he was not the creator of his new work, but merely a reporter. God had provided the inspiration, leaving Cantor only responsible for the way in which his papers were written, for the organization and style, but not for their content. Cantor claimed and believed in the absolute truth of his ‘theories’ because they had been revealed to him. Thus, Cantor saw himself as God’s messenger, and he desired to use mathematics to serve the Christian Church.”
You throw a tiny pebble into the pool, and even before it hits, the fish seem to swim away. “Like Pythagoras, Cantor also believed that numbers (particularly his transfinite numbers) were externally existing realities in the mind of God. They followed God-given laws, and Cantor believed it was possible to argue their existence based on God’s perfection and power. In fact, Cantor said that it would have diminished God’s power had God only created finite numbers. On the other hand, Cantor’s love of the infinite had a distinctly anti-Pythagorean flavor. Pythagoras believed infinity was the destroyer in the universe, the malevolent annihilator of worlds. If mathematics were war, the struggle was between the finite and infinite. The Pythagoreans became obsessed with infinity, and they concluded that numbers closest to one (and finiteness) were the most pure. Numbers beyond the range of ten were further from one and were less important. Cantor would not have agreed.”
“Sir, it would be intriguing to gather Pythagoras, Cantor, and Goedel in a small room with a single blackboard to debate their various ideas on mathematics and God.”
“You bet! What profound knowledge might we gain if we had the power to bring together great thinkers of various ages for a conference on God and mathematics? Would a round-table discussion with Pythagoras, Cantor, and Goedel produce less interesting ideas than one with Newton and Einstein? Could ancient mathematicians contribute any useful ideas to modern mathematicians? Would a meeting of time-traveling mathematicians offer more to humanity than other scientists, for example biologists or sociologists?” You pause. “These are all fascinating questions. I don’t have the answers.”
The three of you stare at the school of fish and watch them move in synchrony, despite their lack of eyes. The resulting patterns are hypnotic, like the reflections from a hundred pieces of broken glass. You imagine that the senses place a filter on how much humans can perceive of the mathematical fabric of the universe. If the universe is a mathematical carpet, then all creatures are looking at it through imperfect glasses. How might humanity perfect those glasses? Through drugs, surgery, or electrical stimulation of the brain? Probably our best chance is through the use of computers.
THE HISTORY AND SCIENCE BEHIND THE SCIENCE FICTION
“Proofs” of God in Science Fiction
Science fiction, like science, is an organized system that, for many, takes the place of religion in the modern world by attempting a complete explanation of the universe. It asks the questions—where did we come from? why are we here? where do we go from here?—that religions exist to answer. That is why religious science fiction is a contradiction in terms although science fiction about religion is commonplace.
—James Gunn, The New Encyclopedia of Science Fiction, 1988
The brain, knowing that a person can’t live forever, rationalizes a future, other-dimensional world in which immortality is possible.
—Philip Jose Farmer
Perhaps the most famous computer proofs of God’s existence come from the realm of science fiction. One favorite example is Arthur C. Clarke’s “The Nine Billion Names of God” (1953). In this story, Tibetan monks install a computer to calculate and list all possible names of God. Western computer technicians soon learn that when the monks complete their computer explorations, humanity’s reason for existence will end. Unfortunately, the technicians learn of the computer too late—just as the project reaches its goal. The technicians look up into the sky, and, “Overhead, without any fuss, the stars were going out.” Interestingly, in Clarke’s next short story “The Star” (1955), a Jesuit scientist comes to the conclusion that the Star of Bethlehem was actually a supernova which simultaneously guided the wise men to Jesus and destroyed an advanced civilization. The Jesuit struggles to understand why a supernova which annihilated a beautiful, harmless civilization was also the harbinger of hope and salvation on Earth.
In Frederic Brown’s “Answer” (1954), computers on many planets are linked together and asked, “Does God exist?” After some time, the computers answer: “He does now.”
There are many examples where religion and science fiction intersect. Amazingly, one science-fiction writer, L. Ron Hubbard, actually created a religion called Scientology which is practiced by many followers today on Earth. Scientology evolved from dianetics, a method of introspection and discussion invented by Hubbard. Using dianetics, followers attempt to attain mental and physical health. Hubbard first published the theory in Astounding Science Fiction magazine in 1950. In the mid-1950s, Scientology took on more religious tenets including the concept of the Thetan, an internal spirit which is endlessly reincarnated.
Here are some additional examples. In one famous science fiction novel, Canticle for Leibowitz (1959), Walter Miller describes how post-nuclear-holocaust monasteries collect blueprints and technological artifacts in the same way that medieval monasteries preserved classical manuscripts. Olaf Stapeldon in his book The Star Maker (1937) suggests that the stars are sentient and responsible for life on their planets. (Interestingly, The Star Maker was not published as science fiction.) In L. P. Gratacap’s The Certainty of a Future Life in Mars (1903), Mars is the location of Heaven and is stuffed with souls. In John Jacob Astor’s A Journey in Other Worlds (1894), spirits are found on Saturn.
Doomsday is a popular theme for science fiction writers. For example, in Camille Flammarion’s The End of the World (1893), the pope and all the clergy pray for the world to be saved from an approaching meteor, but the meteor hits the Vatican, and the book hints that this was God’s intention.
In Nils Parling’s The Cross (1957), a born-again preacher drags a giant, American, atomic cannon around Europe after the Third World War. The cannon, which he calls the fist of God, is thought to be unloaded. Unfortunately, this is not true, and the cannon fires, bringing about an end to higher civilization. The author suggests this is God’s way of returning humanity to an ignorant state.
Philip K. Dick wrote about God in Our Friends from Frolix 8 (1970). The lines I recall most vividly are, “God is dead. They found his carcass in 2019. Floating out in space near Alpha.”
I have also touched on the topic of God and mathematics in my own science fiction. For example, in Chaos in Wonderland there is a religion devoted to the fractal Mandelbrot set, an intricate mathematical object. (See Chapter 13 for more information on fractals.) Mandelbrot sets also appear on mezuzahs hung on doors and in chapels. I also collaborated with Don Webb on a short story titled “To the Valley of the Sea Horses” that appears in Keys to Infinity. The story describes a billionaire’s mystical encounter with love, God, and fractals.
Background on Kurt Goedel
Theology is a branch of physics.… Physicists can infer by calculation the existence of God and the likelihood of the resurrection of the dead to eternal life in exactly the same way as physicists calculate the properties of the electron.
—Frank Tipler, The Physics of Immortality
A friend of mine once was so struck by [a recursive plot’s] infinitely many infinities that he called it “a picture of God,” which I don’t think is blasphemous at all.
—Douglas Hofstadter, Goedel Escher Bach
In this chapter, we briefly mentioned historical examples of the co-mingling of religion and mathematics. Perhaps the most interesting example of a mathematician studying cosmic questions is Austrian mathematician Kurt Goedel (1906–1978) (also spelled Gödel). Sometime in 1970, Goedel’s mathematical proof of the existence of God began to circulate among his colleagues. The proof was less than a page long and caused quite a stir. Before presenting the essence of his proof in Postscript 1, I want to tell you a little about Goedel. His academic credits were impressive. For example, he was a respected mathematician and a member of the faculty of the University of Vienna starting in 1930. He also was a member of the Institute of Advanced Study in Princeton, New Jersey. He emigrated to the United States in 1940.
Goedel is most famous for his theorem that demonstrated there must be true formulas in mathematics and logic that are neither provable nor disprovable, thus making mathematics essentially incomplete. (This theorem was first published in 1931 in Monatshefte für Mathematik und Physick (volume 38).) Goedel’s theorem had quite a sobering effect upon logicians and philosophers because it implies that within any rigidly logical mathematical system there are propositions or questions that cannot be proved or disproved on the basis of axioms within that system, and therefore it is possible for basic axioms of arithmetic to give rise to contradictions. The repercussions of this fact continue to be felt and debated. Moreover, Goedel’s article in 1931 put an end to a century’s long attempt to establish axioms that would provide a rigorous basis for all of mathematics.
Over the span of his life, Goedel kept voluminous notes on his mathematical ideas. Some of his work is so complex that mathematicians believe many decades will be required to decipher all of it. Author Hao Wang writes on this very subject in his book Reflections on Kurt Goedel (1987):
The impact of Goedel’s scientific ideas and philosophical speculations has been increasing, and the value of their potential implications may continue to increase. It may take hundreds of years for the appearance of more definite confirmations or refutations of some of his larger conjectures.
Goedel himself spoke of the need for a physical organ in our bodies to handle abstract theories. He also suggested that philosophy will evolve into an exact theory “within the next hundred years or even sooner.” He even believed that humans will eventually disprove propositions such as “there is no mind separate from matter.”
Background on Cantor
Cantor was careful to stress that despite the actual infinite nature of the universe, and the reasonableness of his conjecture that corporeal and aetherical monads were related to each other as powers equivalent to transfinite cardinals x0 and x1, this did not mean that God necessarily had to create worlds in this way.
—Joseph Dauben, Georg Cantor, 1979
If the universal resurrection is accomplished by reassembling the original atoms which made up the dead, would it not be logically impossible for God to resurrect cannibals? Every one of their atoms belongs to someone else.
—Frank Tipler, The Physics of Immortality
Goedel was not the only mathematician to use mathematics to prove or imply the existence of God. As a second example, let us consider Georg Cantor (1845–1918), a German mathematician who also delved into the arena of theomatics.
Cantor was interested in different levels of infinity and in transfinite numbers. A transfinite number is an infinite cardinal or ordinal number. (A cardinal number is a whole number, an integer, used to specify how many elements there are in a set. An ordinal number is considered as a place in the ordered sequence of whole numbers. For example, it is used in counting as first, second, third, fourth, etc., to nth in a set of n elements.) The smallest transfinite number is called “aleph-nought” (written as N0), which counts the number of integers. If the number of integers is infinite (N0), are there yet higher levels of infinity? It turns out that even though there are an infinite number of integers, rational numbers (numbers which can be expressed as fractions), and irrational numbers (like 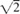 = 1.41 … which cannot be expressed as a fraction), the infinite number of irrationals is in some sense greater than the infinite number of rationals and integers. To denote this difference, mathematicians refer to the infinity of rationals or integers as N0 and the infinite number of irrationals as C which stands for the cardinality of the “continuum.” There is a simple relationship between C and N0. It is C = 2N0. The “continuum hypothesis” states that C = N1; however, the question of whether or not C truly equals N1 is considered undecidable. In other words, great mathematicians such as Kurt Goedel proved that the hypothesis was a consistent assumption in one branch of mathematics. However, another mathematician Paul Cohen proved that it was also consistent to assume the continuum hypothesis is false!
= 1.41 … which cannot be expressed as a fraction), the infinite number of irrationals is in some sense greater than the infinite number of rationals and integers. To denote this difference, mathematicians refer to the infinity of rationals or integers as N0 and the infinite number of irrationals as C which stands for the cardinality of the “continuum.” There is a simple relationship between C and N0. It is C = 2N0. The “continuum hypothesis” states that C = N1; however, the question of whether or not C truly equals N1 is considered undecidable. In other words, great mathematicians such as Kurt Goedel proved that the hypothesis was a consistent assumption in one branch of mathematics. However, another mathematician Paul Cohen proved that it was also consistent to assume the continuum hypothesis is false!
Interestingly, the number of rational numbers is the same as the number of integers. The number of irrationals is the same as the number of real numbers. (Mathematicians usually use the term “cardinality” when talking about the “number” of infinite numbers. For example, true mathematicians would say that the “cardinality” of the irrationals is known as the continuum.)
What do we do with the paradox of the continuum hypothesis? Cantor’s colleague, Constantin Gutberiet, believed that God could resolve the problem of the continuum hypothesis. How many of the great mathematical paradoxes would melt away if humanity had a higher level of intelligence? How many would remain because they are somehow part of the mathematical tapestry underpinning our universe? These are questions not easily answered, at least not by Homo sapiens. Our minds have not sufficiently evolved to comprehend all the mysteries of God and mathematics.
A dog cannot understand Fourier transforms or gravitational wave theory. Human forebrains are a few ounces bigger than a dog’s, and we can ask many more questions than a dog. Linguist Noam Chomsky once noted that a rat can learn to turn left at every second fork in a maze, but not at every fork corresponding to a prime number. The human mind, limited by the same kinds of biological constraints as the rat, may reach the edge of its ability to comprehend. We are flesh and blood, not gods. Are there facets of the universe we can never know? Are there questions we can’t ask? Our brains, which evolved to help us find food on the African plains, are not constructed to penetrate all the enigmas in the infinite mathematical cloak of our universe.
Deciphering the Mathematical Loom
Au fond de l’Inconnu pour trouver du nouveau. [Into the depths of the Unknown in quest of something new.]
—Charles Baudelaire, Le Voyage
In the fictional part of this chapter, the universe was likened to a mathematical carpet which is perceived by creatures looking at it through imperfect glasses. Computers may allow humanity to perfect those glasses. The beauty and importance of computers lie mainly in their usefulness as a tool for reasoning, creating, and discovering. Computers are one of our most important tools for reasoning beyond our own intuition.
We live in a civilization where numbers play a role in virtually all facets of human endeavor. Even in our daily lives we encounter multidigit zip-codes, social security numbers, credit card numbers, and phone numbers. In many ways the requirements for ordinary living are a great deal more complicated than ever before. Digits … digits … digits.… It all seems so dry sometimes. And yet, when one gazes at a page in a scientific journal and sees a set of complicated-looking equations in scientific texts, a sense of satisfaction is generated: The human mind, when aided by numbers and symbols, is capable of expressing and understanding concepts of great complexity. Ever since “visionary” mathematical and physical relations trickled like rain onto the rooftop of 20th-century humans, we have begun to realize that some descriptions of nature lie beyond our traditional, unaided ways of thinking.
The expression of complicated relations and equations is one magnificent step; insight gained from these relations is another. Today, computers with graphics can be used to produce representations of data from a number of perspectives and to characterize natural phenomena with increasing clarity and usefulness. “Mathematicians couldn’t solve it until they could see it!” a caption in a popular scientific magazine recently exclaimed when describing work done on curved mathematical surfaces. In addition, cellular automata and fractals—classes of simple mathematical systems with exotic behavior—are beginning to show promise as models for a variety of physical processes. Today, in almost all branches of the scientific world, computer graphics are helping to provide insight and to reveal hidden relationships in complicated systems.
Today, computer calculations are now beginning to radically change how scientists pursue and conceptualize problems, and computer models open up entire new areas of exploration. In fact, of all the changes in scientific methodology, probably none is more important than the use of computers. The sheer amount of data generated by experiments is so large that comparisons and conclusions could not be made without computers. For example, massive DNA sequences have been uncovered—and only with the computer can hidden correlations be found within these bases in the genetic materials of organisms. Not unlike the search for extraterrestrial signals from space, scientists try to reconstruct messages and patterns in DNA strands, mathematical progressions, and a range of natural phenomena.
The remarkable panoply of computer applications is growing: Computers play a role in the design of other computers, in our understanding of molecular biology and evolution, and in processing images from outer space. The search for extraterrestrial intelligence employs the automatic detection of interstellar signals and requires sophisticated computers.
If the properties we assign to the natural world are partly expressions of the way we think and our capacity for understanding, then the introduction of new tools such as the computer will change those properties. The computer, like a microscope, expands the range of our senses. The world made visible by the computer seems limitless. In fact, in the next decade, almost all advances in science and art will rely partly on the computer and advanced technology. Moreover, humans will not be able to rely on any one single field of knowledge to make significant advances. Indeed, the computer of the 21st century will touch every aspect of our daily life, and enhance our creativity in all areas of artistic and intellectual expression. We’ll all be peering into newly discovered regions of the mathematical loom—perhaps limited only by computers and our imagination.

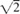 = 1.41 … which cannot be expressed as a fraction), the infinite number of irrationals is in some sense greater than the infinite number of rationals and integers. To denote this difference, mathematicians refer to the infinity of rationals or integers as N0 and the infinite number of irrationals as C which stands for the cardinality of the “continuum.” There is a simple relationship between C and N0. It is C = 2N0. The “continuum hypothesis” states that C = N1;
= 1.41 … which cannot be expressed as a fraction), the infinite number of irrationals is in some sense greater than the infinite number of rationals and integers. To denote this difference, mathematicians refer to the infinity of rationals or integers as N0 and the infinite number of irrationals as C which stands for the cardinality of the “continuum.” There is a simple relationship between C and N0. It is C = 2N0. The “continuum hypothesis” states that C = N1;