Introduction
I have always thought it curious that, while most scientists claim to eschew religion, it actually dominates their thoughts more than it does the clergy.
—Astrophysicist Fred Hoyle
Introduction
I have always thought it curious that, while most scientists claim to eschew religion, it actually dominates their thoughts more than it does the clergy. —Astrophysicist Fred Hoyle |
|
Mathematical inquiry lifts the human mind into closer proximity with the divine than is attainable through any other medium.
—Hermann Weyl (1885–1955)
Mathematics and mysticism have fascinated humanity since the dawn of civilization. Throughout history, numbers held certain powers that made it possible for mortals to seek help from spirits, perform witchcraft, and make prayers more potent. Numbers have been used to predict the end of the world, to raise the dead, to find love, and to prepare for war. Even today, serious mathematicians sometimes resort to mystical or religious reasoning when trying to convey the power of mathematics.
Has humanity’s long-term fascination with mathematics arisen because the universe is constructed from a mathematical fabric? In 1623, Galileo Galilei echoed this belief by stating his credo: “Nature’s great book is written in mathematical symbols.” Plato’s doctrine was that God is a geometer, and Sir James Jeans believed God experimented with arithmetic. Sir Isaac Newton supposed that the planets were originally thrown into orbit by God, but even after God decreed the law of gravitation, the planets required continual adjustments to their orbits.
Astronomy by Charles-Nicolas Cochin The Younger (1715–1790)
Is God a mathematician? Certainly, the world, the universe, and nature can be reliably understood using mathematics. Nature is mathematics. For example, the arrangement of seeds in a sunflower can be understood using Fibonacci numbers (1, 1, 2, 3, 5, 8, 13 …), named after the Italian merchant Leonardo Fibonacci of Pisa. Except for the first two numbers, every number in the sequence equals the sum of the two previous. Sunflower heads, like other flowers, contain two families of interlaced spirals—one winding clockwise, the other counterclockwise. The number of seeds and petals are almost always Fibonacci numbers.
The shape assumed by a delicate spider web suspended from fixed points, or the cross-section of sails bellying in the wind, is a catenary—a simple curve defined by a simple formula. Seashells, animal’s horns, and the cochlea of the ear are logarithmic spirals which can be generated using a mathematical constant known as the golden ratio. Mountains and the branching patterns of blood vessels and plants are fractals, a class of shapes which exhibit similar structures at different magnifications. Einstein’s E = mc2 defines the fundamental relationship between energy and matter. And a few simple constants—the gravitational constant, Planck’s constant, and the speed of light—control the destiny of the universe. I do not know if God is a mathematician, but mathematics is the loom upon which God weaves the fabric of the universe.
Fractal fern exhibiting self-similar branching, that is, similar structures repeated at different size scales. A single branch of the fern looks like a miniature copy of the entire fern.
Physicists are excited about discovering how reality behaves in terms of mathematical descriptions. This process is akin to discovering some hidden presence in the behavior of the universe—a gnosis. In this sense, physics is the inheritor of the tradition of Pythagoras.
—Anonymous IBM physicist
Marilyn vos Savant is listed in the Guinness Book of World Records as having the highest IQ in the world—an awe-inspiring 228. She is author of several delightful books and wife of Robert Jarvik, M.D., inventor of the Jarvik 7 artificial heart. Her column in Parade magazine is read by 70 million people every week. One of her readers once asked her, “Why does matter behave in a way that is describable by mathematics?” She replied:
The classical Greeks were convinced that nature is mathematically designed, but judging from the burgeoning of mathematical applications, I’m beginning to think simply that mathematics can be invented to describe anything, and matter is no exception.
Marilyn vos Savant’s response is certainly one with which many people would agree. However, the fact that reality can be described or approximated by simple mathematical expressions suggests to me that nature has mathematics at its core. Formulas like E = mc2,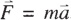 
, 1 + eiπ = 0, and λ = h/mv all boggle the mind with their compactness and profundity. E = mc2 is Einstein’s equation relating energy and mass. 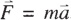Newton’s second law: force acting on a body is proportional to its mass and its acceleration. 1 + eiπ = 0 is Euler’s formula relating three fundamental mathematical terms: e, π, and i. The last equation, λ = h/mv, is de Broglie’s wave equation indicating matter has both wave and particle characteristics. Here the Greek letter lambda (λ) is the wavelength of the wave-particle, and m is its mass. These examples are not meant to suggest that all phenomena, including subatomic phenomena, are described by simple-looking formulas; however, as scientists gain more fundamental understanding, they hope to simplify many of the more unwieldy formulas.
I side with both Martin Gardner and Rudolf Carnap who I interpret as saying: nature is almost always describable by simple formulas not because we have invented mathematics to do so but because of some hidden mathematical aspect of nature itself. For example, Martin Gardner in his classic 1985 essay “Order and Surprise” writes:
If the cosmos were suddenly frozen, and all movement ceased, a survey of its structure would not reveal a random distribution of parts. Simple geometrical patterns, for example, would be found in profusion—from the spirals of galaxies to the hexagonal shapes of snow crystals. Set the clockwork going, and its parts move rhythmically to laws that often can be expressed by equations of surprising simplicity. And there is no logical or a priori reason why these things should be so.
Here Gardner suggests that simple mathematics govern nature from molecular to galactic scales.
Rudolf Carnap, an important 20th century philosopher of science, profoundly asserts:
It is indeed a surprising and fortunate fact that nature can be expressed by relatively low-order mathematical functions.
To best understand Carnap’s idea, consider the first great question of physics: “How do things move?” Imagine a universe called JUMBLE where Kepler looks up into the heavens and finds that most planetary orbits cannot be approximated by ellipses but by bizarre geometrical shapes that defy mathematical description. Imagine Newton dropping an apple whose path requires a 100-term equation to describe. Luckily for us, we do not live in JUMBLE. Newton’s apple is a symbol of both nature and simple arithmetic from which reality naturally evolves.
Had Newton not been steeped in alchemical and other magical learning, he would never have proposed forces of attraction and repulsion between bodies as the major feature of his physical system.
—John Henry, Let Newton Be!
In our modern era, God and mathematics are usually placed in totally separate arenas of human thought. But as this book will show, this has not always been the case, and even today many mathematicians find the exploration of mathematics akin to a spiritual journey. The line between religion and mathematics becomes indistinct. In the past, the intertwining of religion and mathematics has produced useful results and spurred new areas of scientific thought. Consider as just one small example numerical calendar systems first developed to keep track of religious rituals. Mathematics in turn has fed back and affected religion because mathematical reasoning and “proofs” have contributed to the development of theology.
In many ways, the mathematical quest to understand infinity parallels mystical attempts to understand God. Both religion and mathematics attempt to express relationships between humans, the universe, and infinity. Both have arcane symbols and rituals, and impenetrable language. Both exercise the deep recesses of our minds and stimulate our imagination. Mathematicians, like priests, seek “ideal,” immutable, nonmaterial truths and then often try to apply these truths in the real world. Some atheists claim another similarity: mathematics and religion are the most powerful evidence of the inventive genius of the human race.
Passion flower. The first Spaniards in South America connected this flower’s structure with signs of Jesus’ Crucifixion: The three upper parts of the pistil were the three nails. The five stamens were the five wounds surrounded by a crown of thorns. The ten “petals” represented the ten apostles of the Crucifixion.
Of course, there are also many differences between mathematics and religion. For example, many of religion’s main propositions are impossible to prove, and religion often relies on faith unaffected by reason. In addition, while various religions differ in their beliefs, there is remarkable agreement among mathematicians. Philip Davis and Reuben Hersh in The Mathematical Experience suggest “all religions are equal because all are incapable of verification or justification.” Similarly, certain valid branches of mathematics seem to yield contradictory or different results, and it seems that there is not always a “right” answer.…
Einstein’s fundamental insights of space/matter relations came out of philosophical musings about the nature of the universe, not from rational analysis of observational data—the logical analysis, prediction, and testing coming only after the formation of the creative hypotheses.
—R. H. Davis, The Skeptical Inquirer, 1995
We can hardly imagine a chimpanzee understanding the significance of prime numbers, yet the chimpanzee’s genetic makeup differs from ours by only a few percentage points. These minuscule genetic differences in turn produce differences in our brains. Additional alterations of our brains would admit a variety of profound concepts to which we are now totally closed. What mathematics is lurking out there which we can never understand? How do our brains affect our ability to contemplate God? What new aspects of reality could we absorb with extra cerebrum tissue? And what exotic formulas could swim within the additional folds? Philosophers of the past have admitted that the human mind is unable to find answers to some of the most important questions, but these same philosophers rarely thought that our lack of knowledge was due to an organic deficiency shielding our psyches from higher knowledge.
If the yucca moth, with only a few ganglia for its brain, can recognize the geometry of the yucca flower from birth, how much of our mathematical capacity is hardwired into our convolutions of cortex? Obviously specific higher mathematics is not inborn, because acquired knowledge is not inherited, but our mathematical capacity is a function of our brain. There is an organic limit to our mathematical depth.
How much mathematics can we know? The body of mathematics has generally increased from ancient times, although this has not always been true. Mathematicians in Europe during the 1500s knew less than Grecian mathematicians at the time of Archimedes. However, since the 1500s humans have made tremendous excursions along the vast tapestry of mathematics. Today there are probably around 300,000 mathematical theorems proved each year.’
In the early 1900s, a great mathematician was expected to comprehend the whole of known mathematics. Mathematics was a shallow pool. Today the mathematical waters have grown so deep that a great mathematician can know only about 5% of the entire corpus. What will the future of mathematics be like as specialized mathematicians know more and more about less and less until they know everything about nothing?
Various species of star corals exhibiting simple geometrical patterns.
More significant mathematical work has been done in the latter-half of this century than in all previous centuries combined.
—John Casti, Five Golden Rules
During their early days, both science and math have been connected with fictitious beliefs. Astronomy was connected with astrology, chemistry with alchemy, and mathematics with numerology. The Loom of God does not neglect this wild side of mathematics and its effect on human belief systems. The initial emphasis will be on Pythagoras, the ancient Greek mathematician whose ideas continue to thrive after three millennia of mathematical science. Philosopher Bertrand Russell once wrote that Pythagoras was one of the most intellectually important men who ever lived, both when he was wise and when he was unwise. Pythagoras was the most puzzling mathematician of history because he founded a numerical religion whose main tenets were transmigration of souls and the sinfulness of eating beans, along with a host of other odd rules and regulations. To the Pythagoreans, mathematics was an ecstatic revelation. They, like modern day fractalists, were akin to musicians. They created pattern and beauty as they discovered mathematical truths. Mathematical and theological blending began with Pythagoras, and eventually affected all religious philosophy in Greece, played a role in religion of the Middle Ages, and extended to Kant in modern times. Bertrand Russell felt that if it were not for Pythagoras, theologians would not have sought logical proofs of God and immortality.
Engraving by French illustrator Gustave Dore (1832–1883) suggesting the mathematical fabric of reality.
An intelligent observer seeing mathematicians at work might conclude that they are devotees of exotic sects, pursuers of esoteric keys to the universe.
—P. Davis and R. Hersh, The Mathematical Experience
Pure mathematics is religion.
—Friedrich von Hardenberg, circa 1801
The emphasis of this book is on theomatics—a word I coined in 1995 to denote the blending of mathematics and religion. I also discuss many end-of-the-world scenarios—from ancient theological prophesies to modern astrophysical predictions. Numbers have played a central role in both religious and scientific apocalypses. To start you on your journey, we will first trace the logic of mathematics far back in time and examine humanity’s search for ultimate answers to the mystery of existence, God, and the universe. The initial focus is around 550 B.C. because numbers had an auspicious reign in ancient Greece, especially for the Pythagoreans, the secret society devoted to exploring the mysteries of numbers. You will soon realize that both ancient and modern mathematicians trespass on territory that is often considered the exclusive province of religion.
There is a harmony in the universe that can be expressed by whole numbers. Numerical patterns describe the arrangement of florets in a daisy, the reproduction of rabbits, the orbit of the planets, the harmonies of music, the relationships between elements in a periodic table. On the controversial side, mathematics and religion have often come together to predict the end of the world, and numbers have been worshipped like gods. In this book, I’ll give some unusual examples of this juxtaposition of God and mathematics, and also describe some of the current astronomical theories for the end of the earth.
Philosophers and writers make statements about mathematics that have religious undertones. For example, author Alan Watts has described mathematicians in the following way:
The pure mathematician is much more of an artist than a scientist. He does not simply measure the world. He invents complex and playful patterns without the least regard for their practical applicability.
Through history, many philosophers and skeptics have probably made similar statements about religion.
Similarly, Aristotle describes mathematics in his Metaphysics: “Those who claim that the mathematics is not concerned with goodness and beauty miss the truth.” Notice that if you were to examine the writings of many philosophers, and replace “mathematics” with the word “religion,” their statements would be equally powerful and comprehensible. Why is this so? (For example, try this with Aristotle’s quotation by replacing “mathematics” with “religion.”) Is it because both mathematics and religion start with a belief (or axiom) system?
One of my favorite quotations describing the mystical side of science comes from Richard Power’s The Gold Bug Variations:
Science is not about control. It is about cultivating a perpetual condition of wonder in the face of something that forever grows one step richer and subtler than our latest theory about it. It is about reverence, not mastery.
Again notice how the word “science” is easily replaced with “religion” or even “art.”
We, while the stars from heaven shall fall, And mountains are on mountains hurled, Shall stand unmoved amidst them all, And smile to see a burning world.
—Millerite Hymn, 1843
Throughout our history, various prophets of doom have predicted the end of the world using arcane mathematical manipulations. The end takes many forms: a huge comet crashing into the Earth, California sliding into the sea, the Apocalypse predicted in the Book of Revelation. No matter what form Doomsday takes, one thing is clear: the end of the world did not only intrigue ancient religious prophets; interest is still strong in our modern society. Just turn on your T.V. any Sunday morning to find some preacher telling you the world is about to end. Popular books predicting imminent disaster always find large and enthusiastic audiences. Today, in the United States there are probably more “doomists” than there ever were in some medieval or Roman town. Some fundamentalist Christians not only believe that there will be a Judgment Day when the world will end, but they also believe that the world should end.
The doomists have never been right—but one day they will be. Certainly the world will come to an end some time in the future, but more on this subject later …
There is no question about there being design in the Universe. The question is whether this design is imposed from the Outside or whether it is inherent in the physical laws governing the Universe. The next question is, of course, who or what made these physical laws?
—Ralph Estling, The Skeptical Inquirer, 1993
This book will allow you to travel through time and space, and you needn’t be an expert in theology or mathematics. To facilitate your journey, I start most chapters with a dialogue between two quirky explorers who are interested in God and mathematics. You are Chief Historian of an intergalactic museum floating in outer space, a teacher and historian. Your able student is a scolex, a member of a race of creatures with bodies made of diamond.2 Their hard bodies shield them from injury. Your personal scolex, Mr. Plex, helps you perform calculations and protects you from the dangers of time travel.
Prepare yourself for a strange journey as The Loom of God unlocks the doors of your imagination with thought-provoking mysteries, puzzles, and problems on topics ranging from Stonehenge to Armageddon. A resource for science fiction writers, a playground for computer hobbyists, an adventure and education for beginning students in theology, history, astronomy, and mathematics, each chapter is a world of paradox and mystery. Often various experiments in each chapter are accompanied by short listings of computer code in the Appendix. Computer hobbyists may use the code to explore a range of topics: from fractals, to asteroid cratering, to perfect numbers. However, the brief computer programs are just icing on the cake. Those of you without computers can still enjoy the journey and conduct a range of thought experiments. Readers of all ages can study theomatics using just a calculator.
As in all my previous books, you are encouraged to pick and choose from the smorgasbord of topics. Many of the chapters are brief and give you just a flavor of an application or method. Often, additional information can be found in the referenced publications. In order to encourage your involvement, I provide computational hints and recipes for producing the computer-drawn figures. For some of you, program code will clarify concepts.
Some information is repeated so that each chapter contains sufficient background information, but I suggest you read the chapters in order as you and Mr. Plex gradually build your knowledge. The basic philosophy of this book is that creative thinking is learned by experimenting.
______________________
An equation for me has no meaning unless it expresses a thought of God.
—Ramanujan (1887–1920)
Let me wrap up by mentioning some other topics you will encounter in this book as you journey from the ancient past to the far future. You’ll meet enigmatic Greek warriors, Kabalists, St. Augustine, and Ramon Lull. You’ll construct numerical gargoyles and visit prehistoric number caves. You’ll hold an Incan fractal quipu in your hand, and discuss Doomsday. Strange numbers will surround you: pentagonal, perfect, oblong, and golden.…
The oldest mathematical tablets found by archeologists date back to 2400 B.C., and I assume that humanity’s urge to create and wonder about mathematics goes back to the earliest protohumans. Numbers were used by the ancient Amerindians, Sumerians, Babylonians, Chinese, Egyptians, and Indians. The Assyrians and Babylonians even assigned sacred deity-numbers to astronomical objects: our Moon was 30 and Venus was 15. Unfortunately, if we attempt to go back beyond the invention of writing, sometime around 6000 years ago in Sumeria, we find ourselves with little information. Mathematical and religious use of numbers before this time will forever remain a mystery.
In closing, let me remind readers that humans are a moment in astronomic time, a transient guest of the Earth. Our minds have not sufficiently evolved to comprehend all the mysteries of God and mathematics. Our brains, which evolved to make us run from lions on the African savannah, are not constructed to penetrate the infinite mathematical veil. And only a fool would try to compress several millennia’s blending of mathematics and religion. We proceed.
