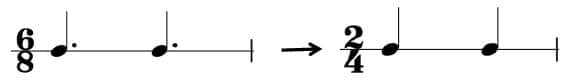part0051

In this lesson, we’re going to play around with meters so that we’ll strengthen our understanding of them. To begin, we’ll rewrite meters and their rhythms as double or half of the original without changing the way they sound.

The main idea behind rewriting any meter is that notes must keep their relative value in their meters. So a note that is worth one beat in one meter will still be worth one beat in the new meter. A note that is worth half a beat in one meter will still be worth half a beat in the new meter and so on.

At first thought, many assume that the double of two-four would be four-four. Although it’s mathematically correct that a measure of four-four can hold double the number of beats as two-four, rhythmically and musically it’s not quite correct.

The character of a meter depends on its pattern of strong and weak beats. In the case of two four, a strong beat occurs every two quarter beats (and so we say that it is in two or that it is duple ). But with the time signature of four-four, the pattern is different. The strongest beat occurs every four quarter beats.

In order to double the meter without changing the character of the rhythm, the new time signature must also be in two; and a measure must also be double the value. The time signature that fulfils these criteria is two-two. While two-four holds two quarter notes per measure, two-two holds two half notes per measure.

Now, what about halving the original? Just as before, we need a time signature that fulfils two criteria: it must be in two just like the original, and a measure must hold half the number of beats. The time signature that fulfils these criteria is two-eight: two eighth note beats per measure.

At this point you might be wondering how it can be that these rhythms sound the same.

This is now a question of tempo . Let’s say the tempo of the original rhythm in two-four is 120 quarter note beats per minute. What should the tempo of the other two rhythms be so that they sound the same as the original?

Since the rhythm in two-four is measured in quarter note beats and there are 120 of them in a minute, then the tempo of the rhythm in two-two will be 120 half note beats per minute because that meter is measured in half notes.

These rhythms sound exactly the same because they consist of the same number of beats per minute and the relative subdivisions are the same. For example, the last measure in the two-four rhythm is a half note (two beats) whereas the last measure in the two-two rhythm is a whole note (also two beats in its meter).

This is an important lesson: meters, rhythms, and tempos are relative to each other and once we can manipulate the notation of rhythm however we like.

Apart from doubling and halving, it’s also possible to rewrite a rhythm from a simple meter to a compound meter (and vice versa) without changing the way it sounds.

As we will see, tuplets will come in handy in such an exercise because we will need to control the subdivisions of beats in order to maintain exactly the same rhythm between simple and compound.

How do we rewrite this into a compound meter? In order to maintain its melodic and rhythmic character, the new meter must also be a triple one. In our previous lessons we saw that a measure in three-four time could quite easily become a measure in nine-eight time if we just add a dot to each beat:

Since it turns out that nine-eight and three-four are related, we can rewrite the rhythm in nine-eight meter. Let’s begin with the triplet units. These are normal in compound meter and so we can just rewrite them as they are. Notice that they are no longer considered triplets because they are not “three notes in the time of two”. Units of three are absolutely normal in compound meters.

Next let’s consider the quarter notes of the original. In three-four meter, any one quarter note takes up one whole beat. In order to maintain the rhythm’s character, these notes should be rewritten so that they still take up a whole beat in the new meter. Since one beat in nine-eight meter is a dotted quarter, the quarter notes in three-four meter become dotted quarter notes in nine-eight meter.

The same principle can apply to the dotted half note in the last measure. This note takes up 3 beats, (the whole measure in three-four meter). The only way to have one note fill up a whole measure in nine-eight is by tying a dotted quarter note to a dotted half note:

What is left is the first measure. It consists of pairs of eighth notes. As we know from previous lessons, the only way to subdivide a beat of a compound time signature into two equal halves is by using the duplet.

Now, let’s go through a similar exercise in the opposite direction: from compound to simple. Here we have a rhythm in six-eight:

As we know, six-eight is a compound duple meter. The extract will be rewritten in a simple duple meter. Remember that to maintain its character, we must maintain the original duple effect. In other words, the new meter must also be in two .

Which simple duple meter shall we use? Removing the dots from the dotted quarter notes of six-eight beats results in two-four, so that is our answer:

Since they both consist of two beats per measure, two-four and six-eight are related.

Let’s begin by rewriting the simplest notes. As we’ve learned, any note that takes up one beat in compound meter will be rewritten as a note that takes up one beat in simple meter too. This will maintain the character of the rhythm.

Notice that the final note of the original (a dotted half note that fills up the last measure) is rewritten as a half note and it fills up the last measure of the new meter.

To finish, we need to rewrite the groups of three eighth notes from the original nine-eight to the new two-four. As we’ve seen before, the only way to subdivide a beat of a simple meter into three equal parts is by employing the triplet.

If this is a little complicated for now, that is perfectly OK. You will come back to this as your understanding of rhythm gets better and better. The most fundamental points here are two: