part0063

Even though this is not a course on piano playing, it’s very useful to become familiar with the keyboard because it makes the visualization of theoretical concepts much easier. For the rest of this course, it will be quite handy to have a piano or keyboard close by.

If you don’t have a piano or keyboard at hand, there are many online apps that you can use for free. Simply search for “virtual keyboard” and many choices will come up.

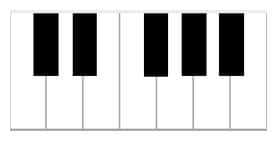
Looking at a piano, we should easily notice that there is a recurring pattern to how the keys are organized. The pattern consists of 12 keys. There are 7 white and 5 black repeating several times across the entire keyboard. In the diagram below, the pattern occurs 3 times:

And here is one instance of it consisting of 12 keys: 7 white and 5 black:

These 12 keys that make up one pattern on the keyboard are the 12 different tones (or pitches) that make up our alphabet of music. The keys going to the left produce lower and lower pitches while those to the right produce higher and higher pitches.

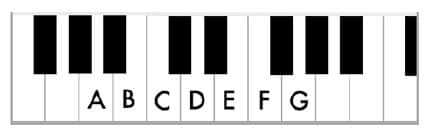
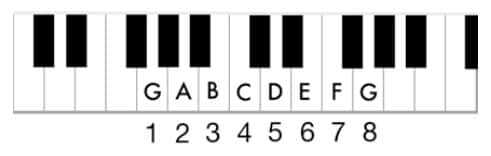
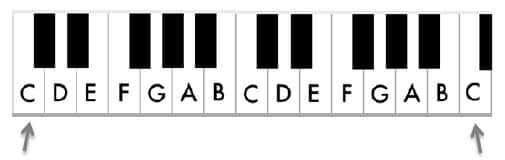
The 7 white key notes are named using the first 7 letters of the English alphabet: A, B, C, D, E, F and G. We will deal with the black keys later.

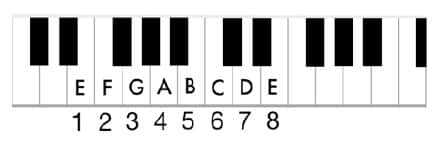
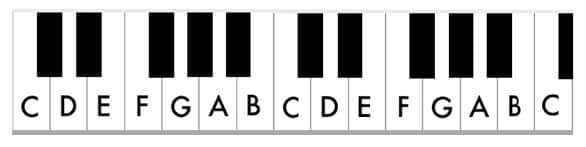
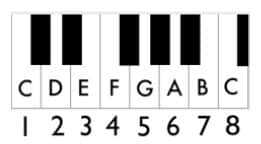
As we’ve seen, the pattern repeats up and down the keyboard, so after the note G , we get another A note and the pattern starts over again from A to G . Here is the keyboard starting from the note C and going through all the white keys twice over.

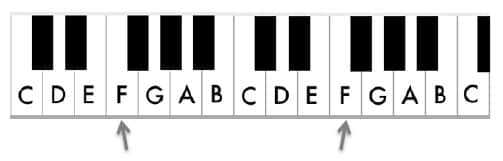
Notice that the distance between two notes that share the same letter name is of 8 keys , or 8 notes. For example, there are 8 notes from this first C note to the next C note:

This distance is called the octave . The word comes from Latin meaning eight and in music we use it to refer to the distance of eight notes. So from one G note to the next G note is the distance of an octave.

And so on-the distance between 2 notes that share the same letter name is that of an octave

Now try it out for yourself. Play and listen to two A notes. Notice how they sound the same except that one is higher (or lighter) and one is lower (or heavier and darker).

When reading about music theory and composition, you will find that the word octave is used in different ways. Keep in mind that it always refers to the same thing: a distance of 8 notes.

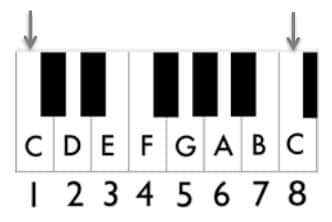
For example, the C note numbered 8 in the picture below is an octave higher than the other C. Or vice-versa: the 1st C note is an octave lower than the other C note.

We can also say that these two F notes are an octave apart . They are 8 notes (or keys) apart.

When counting distance between musical tones, both the first and the last tone are included in the sum. In the example above, the first C note is counted as 1.

In music we have a vast range of notes spanning approximately 8 octaves, and this means that each letter name of the musical alphabet is repeated many times. A standard piano keyboard, for example, has 8 different C notes spread across 88 keys.

In order to distinguish between the notes that share a letter name, the octaves are numbered from zero to nine. This numbering system is called the scientific pitch notation (SPN) and it helps us to refer to a specific note by specifying its octave . In this system, any one octave begins on a C , goes through D , E , F , G , A and ends on a B .

The first octave, then, are the notes:

C0, D0, E0, F0, G0, A0 and B0.

And the second octave comprises the notes:

C1, D1, E1, F1, G1, A1 and B1.

As we’ve said, this numbering will be useful when we speak of specific pitches. The lowest note of the piano, for example, is specifically the note A0 (and not just any A note) while the highest is C8 (and not just any C note). Another example is that the four strings of the violin are tuned specifically at G3, D4, A4 and E5 .