4.1 Al crocevia di tre culture

Ramón Llull (latinizzato in Lullus, e italianizzato come Raimondo Lullo), vissuto tra il 1232 circa e il 1316, è un catalano nato a Maiorca e dunque cresciuto al crocevia di tre culture, la cristiana, l’ebraica e l’islamica. Non solo si è fatto interprete di queste tre tradizioni ma è stato il primo filosofo europeo a scrivere opere dottrinali in volgare, e alcune in rima, con cadenze molto popolari, “affinché si possa mostrare logica e filosofia a chi non sa né latino né arabico” (Compendium 6-9).

Anzitutto però vanno espunte dal corpus lulliano le opere di alchimia, che sono tutte spurie: la fama di Lullo era divenuta tale che vari cultori di scienze occulte gli hanno attribuito le loro opere. Lullo scrisse anche opere mistiche, poetiche, pedagogiche, come il romanzo Blanquerna, o il Libro dell’amico e dell’amato, ma le opere che hanno avuto maggiore influenza sul pensiero successivo sono quelle dedicate alla Ars Magna.

Convertire gli infedeli

Divenuto terziario francescano dopo una vita dissipata, Lullo vuole unificare cristianesimo, ebraismo e islamismo intorno a un nucleo comune di verità condivise, ma in effetti è interessato alla cristianizzazione degli infedeli. L’idea di una conversione degli infedeli è viva nel mondo francescano: si pensi alla missione, nel corso della V crociata, di san Francesco presso il Soldano di Babilonia (ossia il sultano al-Malek el-K-amil del Cairo) nel tentativo di convertirlo al cristianesimo, o agli appelli di Bacone per uno studio delle lingue, in modo da poter parlare agli infedeli e di essere in grado di apprendere da loro tesori di saggezza che essi non avevano diritto di possedere.

Lullo però vuole inventare una sorta di lingua universale che possa convincere chiunque delle verità della religione cristiana sulla base di un calcolo rigorosamente matematico. A questa impresa dedica la maggior parte della sua vita, viaggia in Europa e in Oriente, e la tradizione vuole che sia stato martirizzato dagli infedeli. In effetti subisce un’aggressione a Tunisi, ma muore poi a Maiorca; sarà però beatificato come martire da Pio IX, nel 1850.

4.2 Permutazione, computazione, disposizione

Per capire il progetto lulliano dobbiamo avere presente il concetto di “permutazione”: dati n elementi diversi, il numero di combinazioni possibili, in qualsiasi ordine, è dato dal loro “fattoriale”, che si rappresenta come n! e si calcola come 1.2.3.....n. Un esempio di permutazione è l’anagramma, presente nei testi cabalistici ebraici che probabilmente Lullo conosceva. Salvo che quando noi facciamo anagrammi, delle 24 permutazioni possibili della sequenza ROMA, ad esempio, usiamo solo quelle che nella nostra lingua hanno un senso, come AMOR, MORA, ARMO e RAMO, e scartiamo quelle che non riconosciamo come termini esistenti nel lessico come AOMR, OAMR, MRAO, AROM. Ma in teoria si potrebbero considerare tutte le permutazioni possibili per inventare parole nuove e, a mano a mano che il numero degli elementi aumenta, le permutazioni raggiungerebbero valori vertiginosi. Inoltre si consideri che le ventuno lettere del nostro alfabeto possono dare luogo a più di 51 miliardi di miliardi di sequenze di 21 lettere, con ciascuna lettera diversa dall’altra; se si ammette che alcune lettere vengano ripetute (come nella parola “lettere”, con due “t” e tre “e”), allora il numero di sequenze ammonterebbe a 5 miliardi di miliardi di miliardi.

Importanza della disposizione degli elementi

Non esiste solo la permutazione ma anche la “disposizione” degli elementi. Per esempio, date quattro persone A, B, C, D come posso disporle a coppie, ad esempio a bordo di un aereo che abbia posti affiancati a due a due, ma in modo che conti anche l’ordine (nel caso specifico per definire chi sta dalla parte del finestrino e chi dalla parte del corridoio)? Le nostre persone potranno essere disposte in dodici modi: AB AC AD BA CA DA BC BD CD CB DB DC.

Infine si ha “combinazione” se, da quattro elementi A, B, C, D, si voglia sapere in quanti modi sia possibile appaiarli, ad esempio se fossero soldati da inviare in pattuglia. In tal caso l’ordine non conta (la coppia composta da A e B è la stessa di quella composta da B e A) e le coppie si ridurrebbero a sei: AB AC AD BC BD CD.

4.3 La Tabula generalis e le Figure

Lullo stava dunque manovrando un artificio combinatorio che oggi interessa moltissimo soprattutto gli studiosi di informatica.

Affinché la combinatoria lavori al massimo regime, occorre assumere che non vi siano restrizioni nel pensare tutte le combinazioni possibili. Altrimenti entrano in gioco criteri esterni non solo per discriminare tra i risultati della combinatoria, ma anche per introdurre restrizioni all’interno della combinatoria stessa.

Tabula generalis (Tavola delle dignità) tratta dall’”Ars Magna” di Raimondo Lullo in un’edizione del Cinquecento, Collezione privata

Per esempio, date quattro persone A, B, C, D, ci sono sei modi di combinarle due a due, come abbiamo visto, ma se si tratta di una combinazione intesa alla procreazione, e se A e B sono maschi mentre C e D sono femmine, allora le combinazioni possibili si riducono a quattro; se poi A e C fossero fratello e sorella e dovessimo tener conto del tabù dell’incesto, le possibilità si ridurrebbero a tre.

Ora Lullo ha avuto l’idea veramente rivoluzionaria del calcolo combinatorio ma al tempo stesso ne ha limitato le possibilità.

L’Ars lulliana prevede un alfabeto di nove lettere da B a K che rappresentano nove Principi assoluti (o Dignità divine), ai quali egli associa nove Principi relativi, nove tipi di Questioni, nove Soggetti, nove Virtù e nove Vizi, che sono predicati dei Principi assoluti.

Prima Figura

La cosiddetta Prima Figura dell’Ars lulliana mostra come, assegnati alle lettere i nove Principi assoluti, essi si possono combinare in modo da formare 72 proposizioni del tipo “La bontà è grande” o, leggendo nella direzione inversa, “La grandezza è gloriosa”.

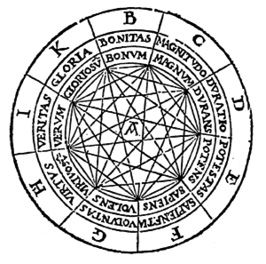
Prima Figura dell’“Ars Magna”

Terza Figura

Sorvoliamo sulla Seconda Figura che non contempla alcuna combinatoria. Più interessante è la Terza Figura dove Lullo considera tutti i possibili appaiamenti tra le lettere. Sembra che escluda le inversioni d’ordine, perché il risultato è di 36 coppie, ma le coppie possibili sono virtualmente 72, perché ciascuna lettera può diventare indifferentemente soggetto e predicato. Così il sistema permette domande come “Se la Bontà sia grande” o “Che cosa è una Bontà grande?” e la terza figura consente, almeno in teoria, 432 proposizioni e 864 questioni.

Terza Figura dell’“Ars Magna”

Quarta Figura

La Quarta Figura è quella che avrà più successo nel corso della tradizione. Qui il meccanismo è mobile, nel senso che si tratta di tre cerchi concentrici di dimensione decrescente, applicati uno sull’altro, e di solito tenuti fissi al centro da una funicella annodata. Nove elementi a gruppi di tre permettono 84 combinazioni (del tipo BCD, BCE, CDE). Se in Ars breu e altrove Lullo parla di 252 combinazioni è perché a ciascuna tripletta possono essere assegnate anche le tre questioni designate dalle lettere che appaiono in tripletta. Ciascuna tripletta genera una colonna di 20 combinazioni (per 84 colonne!) perché Lullo trasforma le triplette in quadruple, inserendo la lettera T. Quando si ottiene una sequenza come BCTC le lettere che precedono la T vanno lette come Principi assoluti, mentre quelle che la seguono vanno lette come Principi relativi. Quindi BCTC andrà letta come: “Se B, la bontà, sia C, grande, in quanto contiene in sé C, e cioè cose concordanti”. Con questo sistema si possono ottenere 1680 combinazioni.

Ma qui emerge subito il primo limite dell’Ars: molte delle combinazioni possibili devono essere respinte sia in base all’esperienza che alle verità di fede. Per esempio la combinatoria permetterebbe di produrre la domanda “se il mondo sia eterno” e la risposta per cui, se il mondo fosse eterno, poiché si è già visto che la bontà è così grande che è eterna, si dovrebbe avere una bontà eterna, e pertanto non ci dovrebbe essere alcun male nel mondo. Ma, obietta Lullo, il male esiste nel mondo, come appare dall’esperienza. Pertanto si deve concludere che il mondo non è eterno. La risposta è dunque negativa non sulla base di quello che la combinatoria permetterebbe di dire, ma secondo quello che il buon cristiano sa già, e cioè che l’eternità del mondo è eresia averroistica.

Pertanto le 1680 sequenze non servono a generare questioni e risposte inedite ma provvedono solo la prova di argomentazioni già collaudate. L’Ars non è uno strumento matematico-logico ma solo uno strumento dialettico, un modo per individuare e ricordare tutti i modi buoni per argomentare in favore di una tesi precostituita.

Quarta Figura dell’“Ars Magna”

4.4 Il fascino dell’arte combinatoria

L’Ars lulliana sedurrà i posteri come se fosse un meccanismo per esplorare una infinità di mondi e di verità possibili (e così accadrà a Niccolò Cusano), con il cabalismo cristiano del Rinascimento, con le vertigini combinatorie con cui hanno giocato matematici e filosofi secentisti, sino alla Dissertatio de arte combinatoria di Leibniz, che penserà a un calcolo fondato su forme simboliche vuote, non ancora ancorate ad alcun contenuto. Ma per Lullo i principi della fede e una cosmologia bene ordinata devono contemperare l’incontinenza della combinatoria. Come Lullo dice nella versione catalana della sua Logica Algazelis: “De la logica parlam tot breu / car a parler avem de Deu” (“Della logica parliamo brevemente / perché bisogna parlare di Dio”).

Rileggere oggi Lullo come se avesse pensato alla computer science significherebbe tradire le sue intenzioni. Ma certamente egli è stato il precursore degli ardimenti successivi che ha ispirato.

LETTURE

Nicolò Cusano

Vol. 2

LETTURE

Cabalismo e lullismo

Vol. 2

LETTURE

Gottfried Leibniz

Vol. 2