
Time passes. You have spent several more years in the employ of your Uncle Fred, and you have truly grown to dread the annual coin-toss sessions. The laws of probability have served you well by providing you with an equal number of heads and tails. Unfortunately, your success and seniority mean that the stakes on each coin toss grow progressively higher. Remember, at the end of each year Uncle Fred adds $5000 to your retirement fund and determines with a coin toss whether your return on the whole account is a gain of 30% (heads) or a loss of 10% (tails). An ever-growing amount of money rides on each toss, and your uncle senses your increasing discomfort.
He makes you another offer. At the end of each year, he will divide your pension account into two equal parts and conduct a separate coin toss for each half.
Just what is your wily uncle up to? Your first instinct is to recoil in horror—if one coin toss unnerves you, surely two must be worse. However, you have an analytical frame of mind, and you begin to dissect his proposition. You realize that there are four possible outcomes for two coin tosses, each with an equal probability:
Outcomes 1 and 4 are the same as they would be in a single coin toss, with the original returns of +30% and −10%, respectively. However, there are two additional possible outcomes, in which the two tosses result in one head and one tail. The total return in these cases is 10% (one-half of +30% plus one-half of −10%).
Since each of the four possible outcomes is equally likely, and in a representative four-year period you will have one of each outcome, you find that your account will increase by a factor of:
1.3 × 1.1 × 1.1 × .9 = 1.4157
Being handy with numbers, you calculate that your annualized return for this two-coin-toss sequence is 9.08%, which is nearly a full percentage point higher than your previous expected return of 8.17% with only one coin toss. Even more amazingly, you realize that your risk has been reduced—with the addition of two returns at the mean of 10%, your calculated standard deviation is now only 14.14%, as opposed to 20% for the single coin toss.
Wise old Uncle Fred has introduced you to the most important concept in portfolio theory:
Dividing your portfolio between assets with uncorrelated results increases return while decreasing risk.
This seems too good to be true. The keyword here is uncorrelated; the result of the first coin toss in no way influences the result of the second toss. Think about it—if the two coin tosses were perfectly correlated and the second coin toss always gave the same result as the first, then we would get only the original +30% and −10% returns.
Those of you with sophisticated investment backgrounds know that a put option on a security or a futures contract sold short will have a highly negative correlation with the return of its underlying asset. However, in that instance the two positions will have nearly opposite returns, with a near zero total portfolio return. A more precise statement would be that two assets with positive returns should not have persistent highly negative correlations.
We would be back to the original single coin toss, with its lower return and higher risk. If the second coin toss were perfectly inversely correlated with the first and always gave the opposite result, then our return would always be 10%. In this case, we would have a 10% annualized long-term return with zero risk! The point cannot be stated strongly enough: mixing assets with unncorrelated returns reduces risk, because when one of the assets is zigging, it is likely that the other is zagging.
In the real world of investing, it is occasionally possible to find two stock or bond classes which have zero correlation, producing a percent or so increase in return and a moderate reduction in risk. Rest assured, however, that in the long run, meaningful negative (inverse) correlations are never seen—this would simply be too good to be true.
The coin-toss example should convince you of the value of diversifying your assets. In the real world of investing, you are faced with a seemingly limitless choice of assets which can be combined into a literally infinite number of portfolios. Yet, for each level of risk you choose to bear, there is only a single “right” mix of assets that will result in the maximum investment return. Even worse, the right, or optimal, asset mix becomes apparent only in retrospect; the optimal mix for the next 20 years is unlikely to look anything like the optimal mix for the past 20 years. How on God’s green earth do you find the best future asset mix?
In order to find the answer, we begin by setting up a “laboratory” which will simulate the performance of complex portfolios. To better understand this, we shall start with some very simple examples.
Example 1. The model consists of only two assets: The first asset, Uncle Fred’s coin toss, with equally likely returns of +30% and −10%, which we shall call stock in this example; and a second asset, with equally likely returns of 0% and +10%, which we shall call bond. Stock has long-term return and risk characteristics similar to those of common stocks, and bond has long-term return and risk characteristics similar to those of five-year Treasury notes. There are four possible outcomes:

You are allowed to choose long-term investment in any combination of these two assets, from 100% stock to 100% bond, with any combination in between. At the end of each year you must rebalance your portfolio back to this combination. Let’s assume that you pick a 50/50 mix of stock and bond. In other words, at the end of each year, 50% of your portfolio is subject to the 0 or +10 (bond) coin toss, and the other 50% is subject to the +30 or −10 (stock) coin toss. If the bond returns +10% and the stock returns −10% for a given year, at the end of that year you now have more bond than stock, and you must sell some bond and use the proceeds to buy more stock. In those years when stock returns 30%, you must similarly exchange enough stock for bond to reset the mix back to 50/50. The reasons for this are several. First and foremost, rebalancing increases long-term portfolio return while reducing risk. Second, failure to rebalance a portfolio of stocks and bonds eventually leads to an almost all-stock portfolio, because of the higher long-term returns of stock, resetting your return-risk combination to a higher level. Last, and most important, the habit of rebalancing instills in the investor the discipline necessary to buy low and sell high.
In this same example, now assume that you have chosen a portfolio of one-quarter (25%) bond and three-quarters (75%) stock. Where Rb and Rs are the returns of bond and stock, respectively, the return for this portfolio in any given period is:
(.25 × Rb) + (.75 × Rs)
Thus, if in a given period the stock return is +30% and the bond return is +10%, then the portfolio return is:
(.25 × 10) + (.75 × 30) = 25%
The returns for each of the four possible outcomes are:
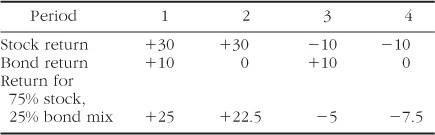
The annualized return for this portfolio is 7.70%, and its SD is 15.05%. First, note that the return of this portfolio is only 0.47% lower than 100% stock, and yet its risk (SD) is decreased by almost 5%. (Put another way, one-quarter of the risk has been eliminated at a cost of only one-seventeenth of the return.) This is simply another demonstration of the benefits of diversification. This paradigm provides you with a simple yet powerful way to study the risk-versus-return characteristics of the most common diversification tool: the stock and bond combination. Those of you who are familiar with spreadsheets will recognize that a simple file analyzing the risk and return from the above paradigm can be written in a few minutes. In Figure 3-1, these values are plotted in a manner identical to Figures 2-9 and 2-10. Remember, as you move up the graph, return increases. As we move from left to right, risk increases.
Figure 3-1. Risk versus reward.
The right side of the graph is not terribly surprising; as you add in small amounts of bond to the stock, there is a dramatic reduction of risk (SD) with a relatively small loss of return. However, the behavior of the left side of the graph is truly remarkable. If you start with an all-bond portfolio, adding small amounts of stock increases return, as expected. However, adding a small amount of stock also decreases the portfolio risk slightly, with the “minimum risk” portfolio consisting of about 7% stock. A stock position of 12% produces the same risk as the all-bond portfolio. Thus, the investor whose sole aim is to minimize risk must of necessity own some stock. This is a phenomenon we shall encounter repeatedly in our study of portfolio behavior.
Example 2. Let’s perform a similar exercise for Uncle Fred’s two-coin-toss portfolio at the beginning of the chapter, where two different assets return either +30% or −10%, and where each asset’s return is independent of the other. To summarize:

Figure 3-2 graphs the return and risk of a portfolio of different mixes of A and B, in the same fashion as was done for Example 1. Since both assets have the same return and SD, you need to plot only half of the points, since a 75/25 mix of A/B will behave the same as a 25/75 mix. The results are clear-cut. The risk lessens (you move toward the left) and return increases (you move up) as you move toward a 50/50 mix. Each point on the graph represents a 5% change in composition, and you can see that most of the gain in return versus risk occurs as you move from 100% of either asset to a 75/25 composition. The trip from 75/25 to 50/50 produces much less additional benefit. The risk and benefit of a 65/35 mix does not differ significantly from the 50/50 mix—less than 0.1% of return and 0.5% of SD. This example makes these key points:
Figure 3-2. Risk versus reward.
1. If two assets have similar long-term returns and risks and are not perfectly correlated, then investing in a fixed, rebalanced mix of the two not only reduces risk but also actually increases return. You already know that the reduced risk is the result of the imperfect correlation between the two assets; a bad result for one asset is quite likely to be associated with a good result for the other, mitigating your loss. The increased return is another facet of the same phenomenon: If a good result for one asset is associated with a bad result for the other, then the rebalancing requirement forces you to sell some of the successful asset (sell high) in order to buy more of the unsuccessful asset (buy low). This excess return is not obtained without rebalancing.
2. If two poorly correlated assets have similar returns and risks, then the optimal mix of the two will be close to 50/50.
3. There is plenty of margin for error available in asset allocation policy. If you are off 10% or 20% from what in retrospect turned out to be the best allocation, you have not lost that much. As we shall see, sticking by your asset allocation policy through thick and thin is much more important than picking the “best” allocation.
The above models have been quite useful for demonstrating the effect of diversification on risk and return of two similar assets (Example 2) and two different assets (Example 1) with zero correlation. Unfortunately, the above examples are no more than useful illustrations of the theoretical benefits of diversified portfolios. In the real world of investing, we must deal with mixes of dozens of asset types, each with a different return and risk. Even worse, the returns of these assets are only rarely completely uncorrelated. Worse still, the risks, returns, and correlations of these assets fluctuate considerably over time. In order to understand real portfolios, we shall require much more complex techniques.
Thus far we have dealt with portfolios with only two uncorrelated components. Two uncorrelated assets may be represented with four time periods as in Uncle Fred’s coin toss, three assets with eight periods, four assets with 16 periods, etc. In the real world of investing, however, it is difficult to find two assets that are uncorrelated, and it is practically impossible to find three. It is absolutely impossible to find more than three mutually uncorrelated assets. The reason for this is simple. A portfolio of two assets has only one correlation. Three assets have three correlations, and four assets have six correlations. (This is the same reason why big offices have messier politics than small ones. A three-person office has three interpersonal relationships; a 10-person office has 45 relationships.)
Real assets are almost always imperfectly correlated. In other words, an above-average return in one is somewhat more likely to be associated with an above-average return in the other. The degree of correlation is expressed by a correlation coefficient. This value ranges from −1 to +1. Perfectly correlated assets have a correlation coefficient of +1, and uncorrelated assets have a coefficient of 0. Perfectly inversely (or negatively) correlated assets have a coefficient of −1. The easiest way to understand this is to plot the returns of two assets against each other for many periods, as is done in Figures 3-3, 3-4, and 3-5.
Figure 3-3. S&P 500/U.S. small stock, correlation of .777.
Figure 3-4. S&P 500/EAFE, correlation of .483.
Figure 3-5. Japan small stock/REIT correlation of .068.
Each figure plots the 288 monthly returns for each asset pair for the 24-year period from January 1975 to December 1998. Each point on the graph represents the return for one of those months; the return for the first asset is read on the x(horizontal) axis, and for the second asset on the y (vertical) axis. If the assets are perfectly correlated, they will all fit on a straight line. (If the correlation is positive, the line will run from lower-left to upper-right; if negative, the line will run from upper-left to lower-right.) If they are uncorrelated, they will be widely scattered.
Figure 3-3 plots the monthly returns for 1975–1998 of the S&P 500 versus U.S. small stocks. Most of the points lie on nearly a straight line; a poor return for one was invariably associated with a poor return for the other. The correlation coefficient of .777 for these two assets is quite high. This graph demonstrates that adding U.S. small stocks to a portfolio of U.S. large stocks does not diminish risk very much, as a poor return for one will be very likely associated with a poor return for the other.
Figure 3-4 plots two loosely correlated assets—U.S. large stocks (S&P 500) and foreign large stocks (EAFE Index). Although there does appear to be a loose relation between the two, it is far from perfect. The correlation coefficient of this pair is .483.
Lastly, Figure 3-5 plots two very poorly correlated assets (correlation coefficient of .068): Japanese small stocks and REITs. This plot is a “scattergram” with no discernable pattern. A good or bad result for one of these assets tells us nothing about the result for the other.
Math Details: How to Calculate a Correlation Coefficient
In this book’s previous versions, I included a section on the manual calculation of the correlation coefficient. In the personal computer age, this is an exercise in masochism. The easiest way to do this is with a spreadsheet. Let’s assume that you have 36 monthly returns for two assets, A and B. Enter the returns in columns A and B, next to each other, spanning rows 1 to 36 for each pair of values.
In Excel, enter in a separate cell the formula = CORREL(A1:A36, B1:B36)
In Quattro Pro, the formula would be @CORREL(A1..A36, B1..B36)
Both of these packages also contain a tool that will calculate a “correlation grid” of all of the correlations of an array of data for more than two assets. Those of you who would like an explanation of the steps involved in calculating a correlation coefficient are referred to a standard statistics text.
Why is this so important? As already discussed the most diversification benefit is obtained from uncorrelated assets. The above analysis suggests that there is not much benefit from mixing domestic small and large stocks and that there is great benefit from mixing REITs and Japanese small stocks. In the real world of investing, this turns out to be the case.
1. The concept of correlation of assets is central to portfolio theory—the lower the correlation, the better.
2. Diversifying your portfolio among uncorrelated assets reduces risk and increases return. It is necessary to rebalance your portfolio periodically to capture this increased return.