Chapter 16. Transforms
Ever since the inception of Cascading Style Sheets (CSS), elements have been rectangular and firmly oriented on the horizontal and vertical axes. A number of tricks arose to make elements look like they were tilted and so on, but underneath it all was a rigid grid. In the late 2000s, an interest grew in being able to break the shackles of that grid and transform objects in interesting ways—and not just in two dimensions.
If you’ve ever positioned an object, whether relatively or absolutely, then you’ve already transformed that object. For that matter, any time you used floats or negative-margin tricks (or both), you transformed an object. All of those are examples of translation, or the movement of an element from where it would normally appear to some other place. With CSS transforms, you have a new way to translate elements, and a whole lot more. Whether it’s as simple as rotating some photographs a bit to make them appear more natural, or creating interfaces where information can be revealed by flipping over elements, or just doing interesting perspective tricks with sidebars, CSS transforms can—if you’ll pardon the obvious expression—transform the way you design.
Coordinate Systems
Before embarking on this journey, let’s take a moment to orient ourselves. Two types of coordinate systems are used in transforms, and it’s a good idea to be familiar with both.
Note
If you’re already well familiar with Cartesian and spherical coordinate systems, particularly as used in computing, feel free to skip to the next section.
The first is the Cartesian coordinate system, or what’s often called the x/y/z coordinate system. This system is a way of describing the position of a point in space using two numbers (for two-dimensional placement) or three numbers (for three-dimensional placement). In CSS, the system uses three axes: the x, or horizontal axis; the y, or vertical axis; and the z, or depth axis. This is illustrated in Figure 16-1.
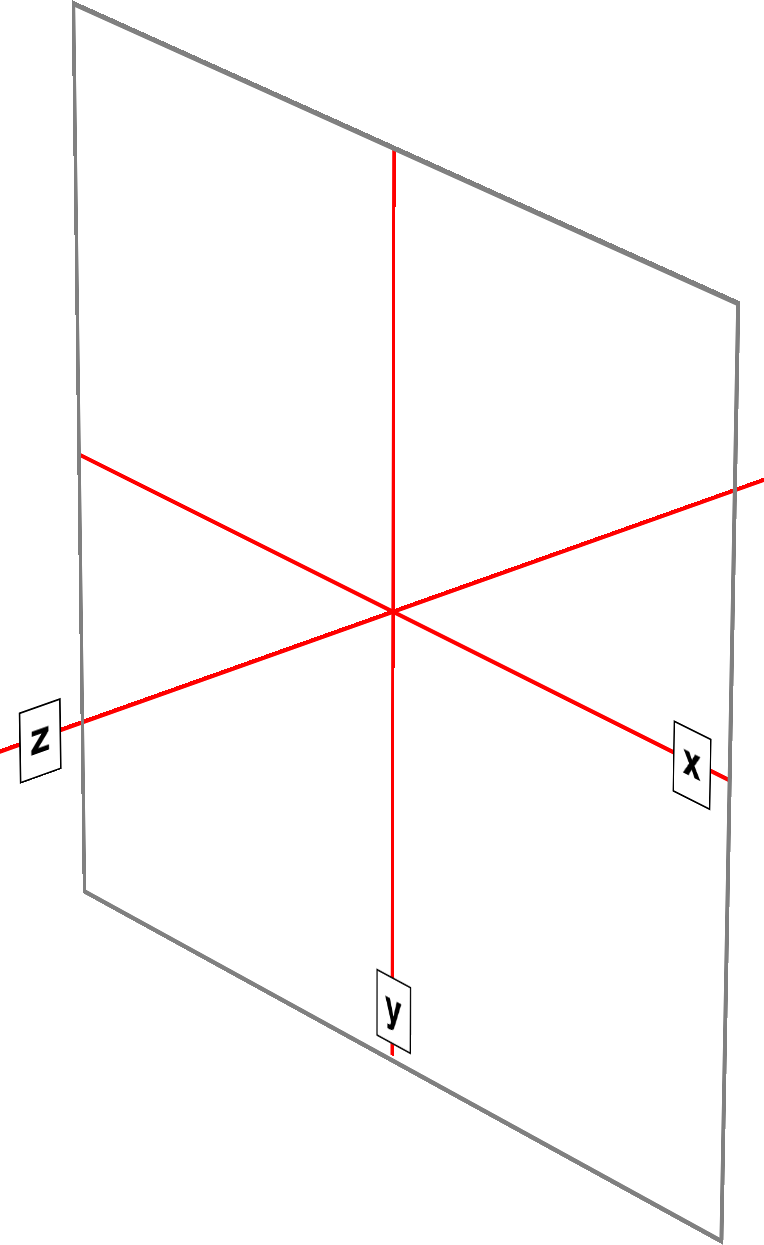
Figure 16-1. The three Cartesian axes used in CSS transforms
For any 2D (two-dimensional) transform, you only need to worry about the x- and y-axes. By convention, positive x values go to the right, and negative values go to the left. Similarly, positive y values go downward along the y-axis, while negative values go upward along the y-axis.
That might seem a little weird, since we tend to think that higher numbers should place something higher up, not lower down, as many of us learned in pre-algebra. (This why the “y” label is at the bottom of the y-axis in Figure 16-1: the labels are placed in the positive direction on all three axes.) If you are experienced with absolute positioning in CSS, think of the top property values for absolutely positioned elements: they get moved downward for positive top values, and upward when top has a negative length.
Given this, in order to move an element leftward and down, you would give it a negative x and a positive y value, like this:
translateX(-5em)translateY(33px)
That is in fact a valid transform value, as we’ll see in just a bit. Its effect is to translate (move) the element five ems to the left and 33 pixels down.
If you want to transform something in three-dimensional space, then you
add a z-axis value. This axis is the one that “sticks out” of the
display and runs straight through your head. In a theoretical sense,
that is. Positive z values are closer to you, and negative z values are
further away from you. In this regard, it’s exactly like the z-index
property.
So let’s say that we want to take the element we moved before and add a z-axis value:
translateX(-5em)translateY(33px)translateZ(200px)
Now the element will appear 200 pixels closer to us than it would be without the z value.
Well you might wonder exactly how an element can be moved 200 pixels closer to you, given that holographic displays are regrettably rare and expensive. How many molecules of air between you and your monitor are equivalent to 200 pixels? What does an element moving closer to you even look like, and what happens if it gets too close? These are excellent questions that we’ll get to later on. For now, just accept that moving an element along the z-axis appears to move it closer or farther away.
The really important thing to remember is that every element carries its own frame of reference and so considers its axes with respect to itself. That is to say, if you rotate an element, the axes rotate along with it, as illustrated in Figure 16-2. Any further transforms are calculated with respect to those rotated axes, not the axes of the display.
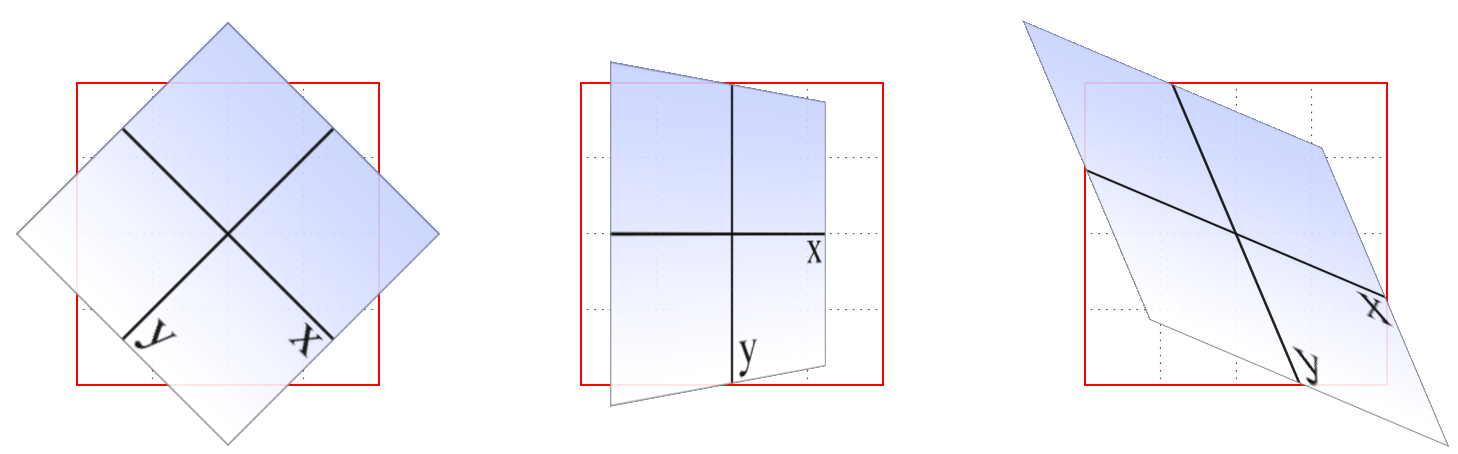
Figure 16-2. Elemental frames of reference
Speaking of rotations, the other coordinate system used in CSS transforms is a spherical system, which describes angles in 3D space. It’s illustrated in Figure 16-3.

Figure 16-3. The spherical coordinate system used in CSS transforms
For the purposes of 2D transforms, you only have to worry about a single 360-degree polar system: the one that sits on the plane described by the x- and y-axes. When it comes to rotations, a 2D rotation actually describes a rotation around the z-axis. Similarly, rotations around the x-axis tilt the element toward or away from you, and rotations around the y-axis turn the element from side to side. These are illustrated in Figure 16-4.
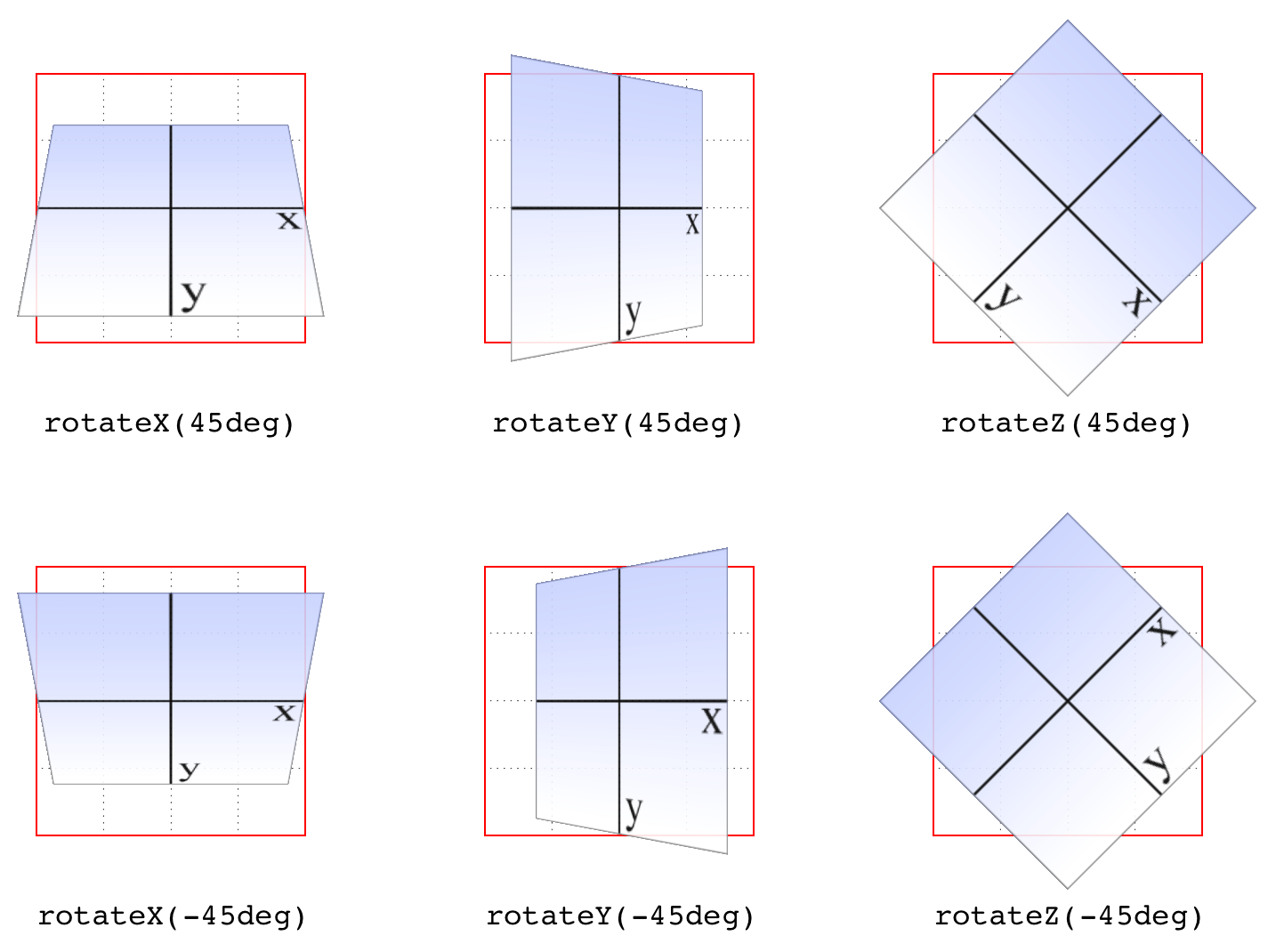
Figure 16-4. Rotations around the three axes
But back to 2D rotations. Suppose you wanted to rotate an element 45 degrees clockwise in the plane of the display (i.e., around the z-axis). The transform value you’re most likely to use is:
rotate(45deg)
Change that to –45deg, and the element will rotate counterclockwise
(anticlockwise for our international friends) around the z-axis. In
other words, it will rotate in the xy plane, as illustrated in Figure 16-5.
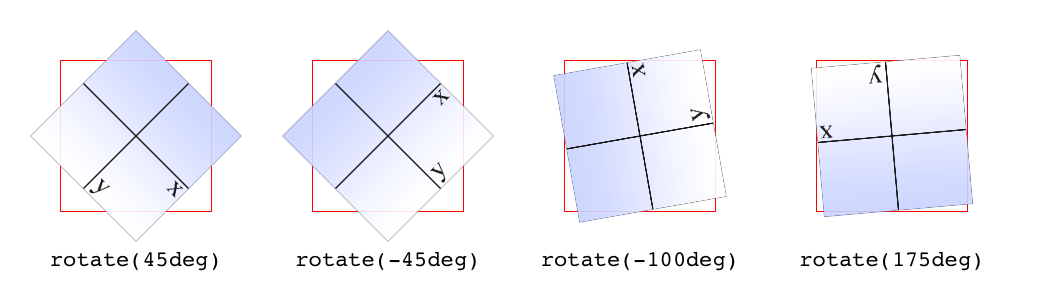
Figure 16-5. Rotations in the xy plane
All right, now that we have our bearings, let’s get started with transforms!
Transforming
There’s really only one property that applies transforms, along with a few ancillary properties that affect exactly how the transforms are applied. We’ll start with the big cheese.
First off, let’s clear up the matter of the bounding box. For any element being affected by CSS, this is the border box; that is, the outermost edge of the element’s border. That means that any outlines and margins are ignored for the purposes of calculating the bounding box.
Note
If a table-display element is being transformed, its bounding box is the table wrapper box, which encloses the table box and any associated caption box.
If you’re transforming a Scalable Vector Graphics (SVG) element with CSS, then its bounding box is its SVG-defined object bounding box.
Note that all transformed elements (i.e., elements with transform set
to a value other than none) have their own stacking context. While the
scaled element may be much smaller or larger than it was before the
transform was applied, the actual space on the page that the element occupies
remains the same as before the transform was applied. This is true for
all the transform functions.
Now, the value entry <transform-list> requires some explanation. This placeholder
refers to a list of one or more transform functions, one after the
other, in space-separated format. It looks like this, with the result
shown in Figure 16-6:
#example{transform:rotate(30deg)skewX(-25deg)scaleY(2);}

Figure 16-6. A transformed div element
The functions are processed one at a time, starting with the first (leftmost) and proceeding to the last (rightmost). This first-to-last processing order is important, because changing the order can lead to drastically different results. Consider the following two rules, which have the results shown in Figure 16-7:
img#one{transform:translateX(200px)rotate(45deg);}img#two{transform:rotate(45deg)translateX(200px);}
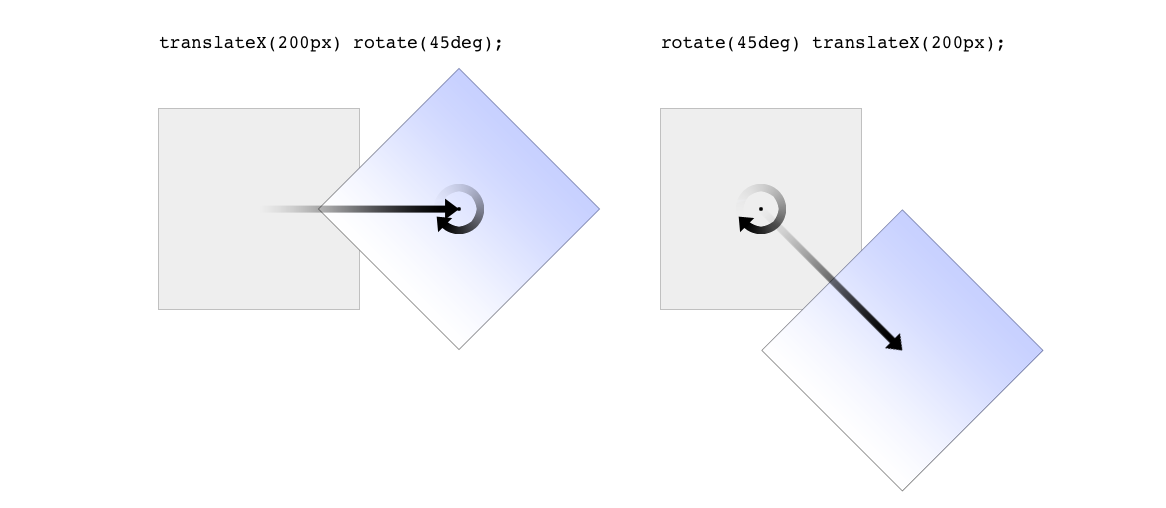
Figure 16-7. Different transform lists, different results
In the first instance, an image is translated (moved) 200 pixels along its x-axis and then rotated 45 degrees. In the second instance, an image is rotated 45 degrees and then moved 200 pixels along its x-axis—that’s the x-axis of the transformed element, not of the parent element, page, or viewport. In other words, when an element is rotated, its x-axis (along with its other axes) rotates along with it. All element transforms are conducted with respect to the element’s own frame of reference.
Compare this to a situation where an element is translated and then scaled, or vice versa; it doesn’t matter which is which, because the end result is the same:
img#one{transform:translateX(100px)scale(1.2);}img#two{transform:scale(1.2)translateX(100px);}
The situations where the order doesn’t matter are far outnumbered by the situations where it does; so in general, it’s a good idea to just assume the order always matters, even when it technically doesn’t.
Note that when you have a series of transform functions, all of them must be properly formatted; that is, they must be valid. If even one function is invalid, it renders the entire value invalid. Consider:
img#one{transform:translateX(100px)scale(1.2)rotate(22);}
Because the value for rotate() is invalid—rotational values must have
a unit—the entire value is dropped. The image in question will just
sit there in its initial untransformed state, neither translated nor
scaled, let alone rotated.
It’s also the case that transforms are not usually cumulative. That is to say, if you apply a transform to an element and then later want to add a transformation, you need to restate the original transform. Consider the following scenarios, illustrated in Figure 16-8:
#ex01{transform:rotate(30deg)skewX(-25deg);}#ex01{transform:scaleY(2);}#ex02{transform:rotate(30deg)skewX(-25deg);}#ex02{transform:rotate(30deg)skewX(-25deg)scaleY(2);}
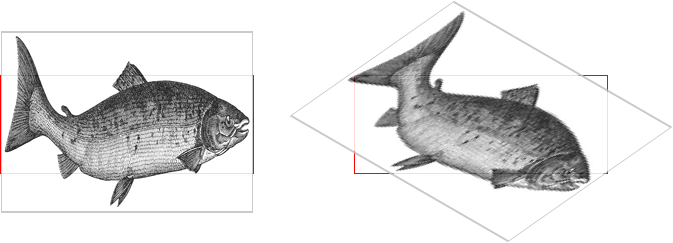
Figure 16-8. Overwriting or modifying transforms
In the first case, the second rule completely replaces the first,
meaning that the element is only scaled along the y-axis. This actually
makes some sense; it’s the same as if you declare a font size and then
elsewhere declare a different font size for the same element. You don’t
get a cumulative font size that way. You just get one size or the other.
In the second example, the entirety of the first set of transforms is
included in the second set, so they all are applied along with the
scaleY() function.
There is an exception to this, which is that animated transforms, whether using transitions or actual animations, are additive. That way, you can take an element that’s transformed and then animate one of its transform functions without overwriting the others. For example, assume you had:
img#one{transform:translateX(100px)scale(1.2);}
If you then animate the element’s rotation angle, it will rotate from its translated, scaled state to the new angle, and its translation and scale will remain in place.
What makes this interesting is that even if you don’t explicitly specify
a transition or animation, you can still create additive transforms via
the user-interaction pseudoclasses, such as :hover. That’s because
things like hover effects are types of transitions; they’re just not
invoked using the transition properties. Thus, you could declare:
img#one{transform:translateX(100px)scale(1.2);}img#one:hover{transform:rotate(-45deg);}
This would rotate the translated, scaled image 45 degrees to its left on hover. The rotation would take place over zero seconds because no transition interval was declared, but it’s still an implicit transition. Thus, any state change can be thought of as a transition, and thus any transforms that are applied as a result of those state changes are additive with previous transforms.
There’s one important caveat: as of this writing, transforms are not
applied to atomic inline-level boxes. These are inline boxes like
spans, hyperlinks, and so on. Those elements can be transformed if their
block-level parent is transformed, in which case they go along for the
ride. But you can’t just rotate a span unless you’ve changed its
display role via display: block, display: inline-block, or something
along those lines. The reason for this limitation boils down to an
uncertainty. Suppose you have a span (or any inline-level box) that
breaks across multiple lines. If you rotate it, what happens? Does each
line box rotate with respect to itself, or should all the line boxes be
rotated as a single group? There’s no clear answer, and the debate
continues, so for now you can’t directly transform inline-level boxes.
The Transform Functions
There are, as of this writing, 21 different transform functions, employing a number of different value patterns to get their jobs done. Table 16-1 provides a list of all the available transform functions, minus their value patterns.
|
|
|
|
|
|
The most common value pattern for transform is a
space-separated list of one or more functions, processed from first
(leftmost) to last (rightmost), and all of the functions must have valid
values. If any one of the functions is invalid, it will invalidate the
entire value of transform, thus preventing any transformation at all.
Translation functions
A translation transform is just a move along one or more axes. For
example, translateX() moves an element along its own x-axis,
translateY() moves it along its y-axis, and translateZ() moves it along its z-axis.
| Functions | Permitted values |
|---|---|
|
<length> | <percentage> |
These are usually referred to as the “2D” translation functions, since they can slide an element up and down, or side to side, but not forward or backward along the z-axis. Each of these functions accepts a single distance value, expressed as either a length or a percentage.
If the value is a length, then the effect is about what you’d expect.
Translate an element 200 pixels along the x-axis with
translateX(200px), and it will move 200 pixels to its right. Change
that to translateX(-200px), and it will move 200 pixels to its left.
For translateY(), positive values move the element downward, while negative
values move it upward, both with respect to the element itself. Thus, if
you flip the element upside down by rotation, positive translateY()
values will actually move the element downward on the page.
If the value is a percentage, then the distance is calculated as a
percentage of the element’s own size. Thus, translateX(50%) will move
an element 300 pixels wide and 200 pixels tall to its right by 150
pixels, and translateY(-10%) will move that same element upward (with
respect to itself) by 20 pixels.
| Function | Permitted values |
|---|---|
|
[ <length> | <percentage> ] [ |
If you want to translate an element along both the x- and y-axes at the
same time, then translate() makes it easy. Just supply the x value
first and the y value second, and it will act the same as if you
combined translateX() translateY(). If you omit the y value, then it’s
assumed to be zero. Thus, translate(2em) is treated as if it were
translate(2em,0), which is also the same as translateX(2em). See
Figure 16-9 for some examples of 2D translation.
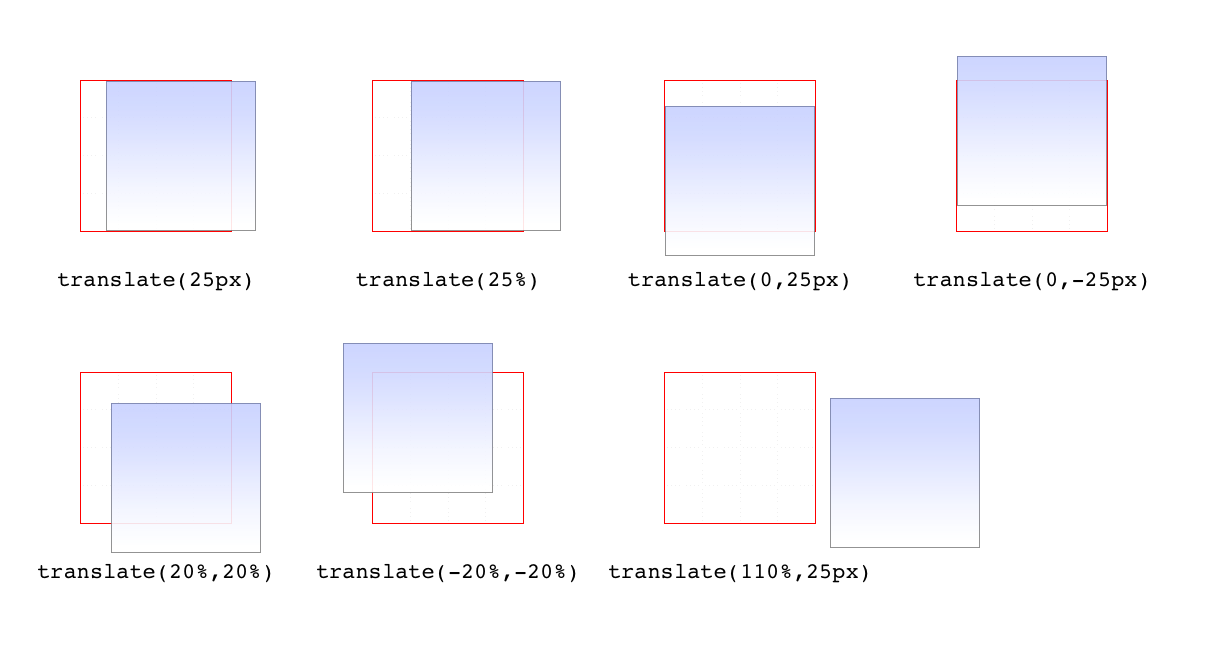
Figure 16-9. Translating in two dimensions
According to the latest version of the specification, both of the 2D translation functions can be given a unitless number. In this case, the number is treated as being expressed in terms of a user unit, which is treated the same as a pixel unless otherwise defined. The CSS specification does not explain how a user unit is otherwise defined; however, the SVG specification does, albeit briefly. In the field, no browser tested as of this writing supported unitless numbers of translation values, so the capability is academic, at best.
| Function | Permitted value |
|---|---|
|
<length> |
This function translates elements along the z-axis, thus moving them
into the third dimension. Unlike the 2D translation functions,
translateZ() only accepts length values. Percentage values are not
permitted for translateZ(), or indeed for any z-axis value.
| Functions | Permitted values |
|---|---|
translate3d() |
[ <length> | <percentage> ], [ <length> | <percentage>], [ <length> ] |
Much like translate() does for x and y translations, translate3d()
is a shorthand function that incorporates the x, y, and z translation
values into a single function. This is handy if you want to
move an element over, up, and forward in one fell swoop. See Figure 16-10
for an illustration of how 3D translation works. There, each arrow
represents the translation along that axis, arriving at a point in 3D
space. The dashed lines show the distance and direction from the origin
point (the intersection of the three axes) and the distance above the xz
plane.
Unlike translate(), there is no fallback for situations where
translate3d() does not contain three values. Thus,
translate3d(1em,-50px) should be treated as invalid by user agents
instead of being assumed to be translate3d(2em,-50px,0).
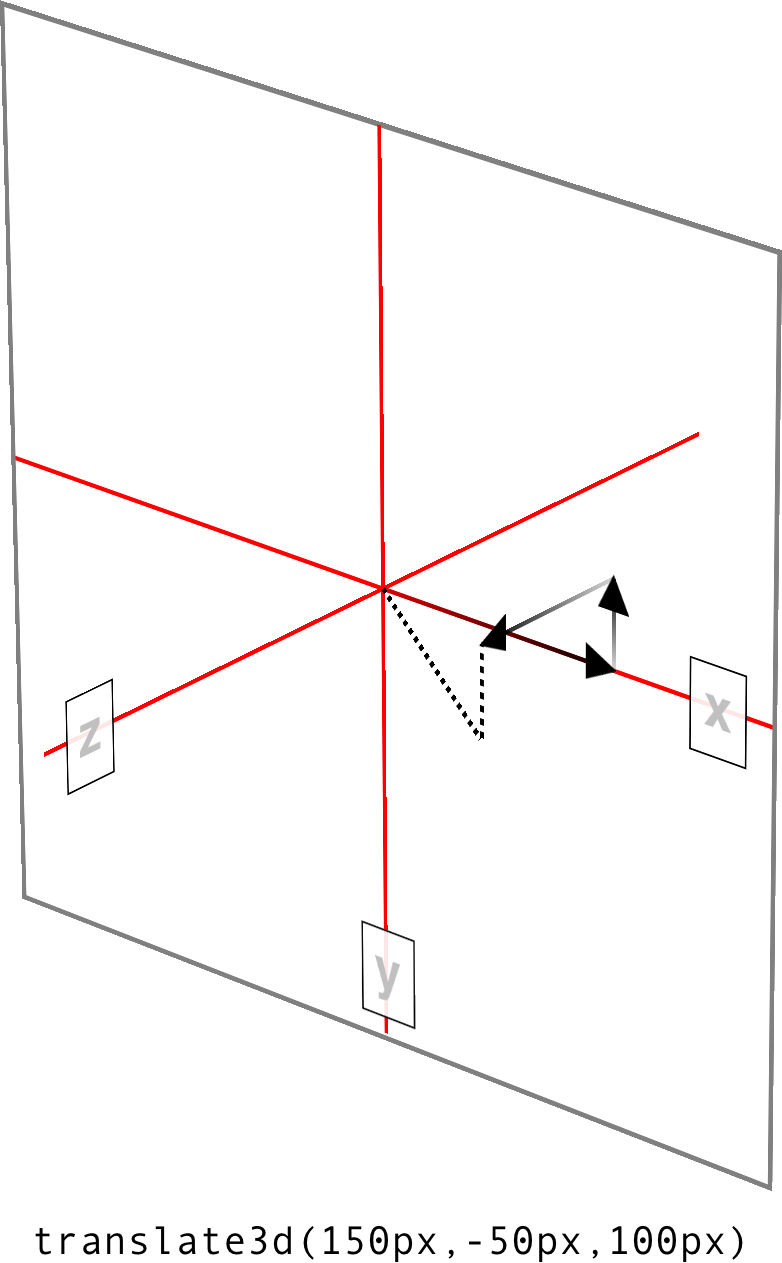
Figure 16-10. Translating in three dimensions
Scale functions
A scale transform makes an element larger or smaller, depending on what value you use. These values are unitless real numbers and are always positive. On the 2D plane, you can scale along the x- and y-axes individually, or scale them together.
| Functions | Permitted value |
|---|---|
|
<number> |
The number value supplied to a scale function is a multiplier; thus,
scaleX(2) will make an element twice as wide as it was before the
transformation, whereas scaleY(0.5) will make it half as tall. Given this, you might expect that percentage values are permissible as scaling values, but they aren’t.
| Function | Permitted value |
|---|---|
|
<number> [ |
If you want to scale along both axes simultaneously, use scale(). The
x value is always first and the y always second, so scale(2,0.5) will
make the element twice as wide and half as tall as it was before being
transformed. If you only supply one number, it is used as the scaling
value for both axes; thus, scale(2) will make the element twice as
wide and twice as tall. This is in contrast to translate(), where an
omitted second value is always set to zero. scale(1) will scale an
element to be exactly the same size it was before you scaled it, as will
scale(1,1). Just in case you were dying to do that.
Figure 16-11 shows a few examples of element scaling, using both the
single-axis scaling functions, as well as the combined scale().

Figure 16-11. Scaled elements
If you can scale in two dimensions, you can also scale in
three. CSS offers scaleZ() for scaling just along the z-axis, and
scale3d() for scaling along all three axes at once. These really only
have an effect if the element has any depth, which elements don’t by
default. If you do make a change that conveys depth—say, rotating an
element around the x- or y-axes—then there is a depth that can be scaled,
and either scaleZ() or scale3d() can do so.
| Function | Permitted value |
|---|---|
|
<number> |
Similar to translate3d(), scale3d() requires all three numbers to be
valid. If you fail to do this, then the malformed scale3d() will
invalidate the entire transform value to which it belongs.
Rotation functions
A rotation function causes an element to be rotated around an axis, or around an arbitrary vector in 3D space. There are four simple rotation functions, and one less-simple function meant specifically for 3D.
| Functions | Permitted values |
|---|---|
|
<angle> |
All four basic rotation functions accept just one value: a degree. This
can be expressed using any of the valid degree units (deg, grad,
rad, and turn) and a number, either positive or negative. If a
value’s number runs outside the usual range for the given unit, it will
be normalized to fit into the accepted range. In other words, a value of
437deg will be tilted the same as if it were 77deg, or, for that
matter, -283deg.
Note, however, that these are only exactly equivalent if you don’t
animate the rotation in some fashion. That is to say, animating a
rotation of 1100deg will spin the element around several times before
coming to rest at a tilt of -20 degrees (or 340 degrees, if you like).
By contrast, animating a rotation of -20deg will tilt the element a
bit to the left, with no spinning; and animating a rotation of
340deg will animate an almost-full spin to the right. All three
animations come to the same end state, but the process of getting there
is very different in each case.
The function rotate() is a straight 2D rotation, and the one you’re
most likely to use. It is equivalent to rotateZ() because it rotates
the element around the z-axis (the one that shoots straight out of your
display and through your eyeballs). In a similar manner, rotateX() causes
rotation around the x-axis, thus causing the element to tilt toward or
away from you; and rotateY() rotates the element around its y-axis, as
though it were a door. These are all illustrated in Figure 16-12.
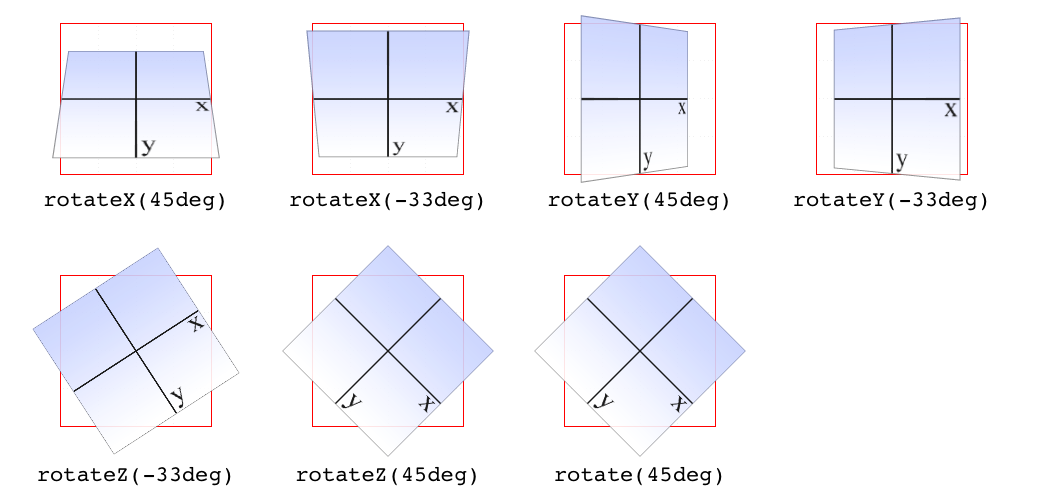
Figure 16-12. Rotations around the three axes
Warning
Several of the examples in Figure 16-12 present a fully 3D
appearance. This is only possible with certain values of the properties
transform-style and perspective, described in sections “Choosing a 3D Style” and “Changing Perspective” and
omitted here for clarity. This will be true throughout this text in any
situation where 3D-transformed elements appear to be fully
three-dimensional. This is important to keep in mind because if you
just try to apply the transform functions shown, you won’t get the same
visual results as in the figures.
| Function | Permitted value |
|---|---|
|
<number>`,` <number>`,` <number>`,` <angle> |
If you’re comfortable with vectors and want to rotate an element through
3D space, then rotate3d() is for you. The first three numbers specify
the x, y, and z components of a vector in 3D space, and the degree value (angle)
determines the amount of rotation around the declared 3D vector.
To start with a basic example, the 3D equivalent to rotate(45deg) is
rotate3d(0,0,1,45deg). This specifies a vector of zero magnitude on
the x- and y-axes, and a magnitude of 1 along the z-axis. In other words,
it describes the z-axis. The element is thus rotated 45 degrees around
that vector, as shown in Figure 16-13. This figure also shows the
appropriate rotate3d() values to rotate an element by 45 degrees
around the x- and y-axes.
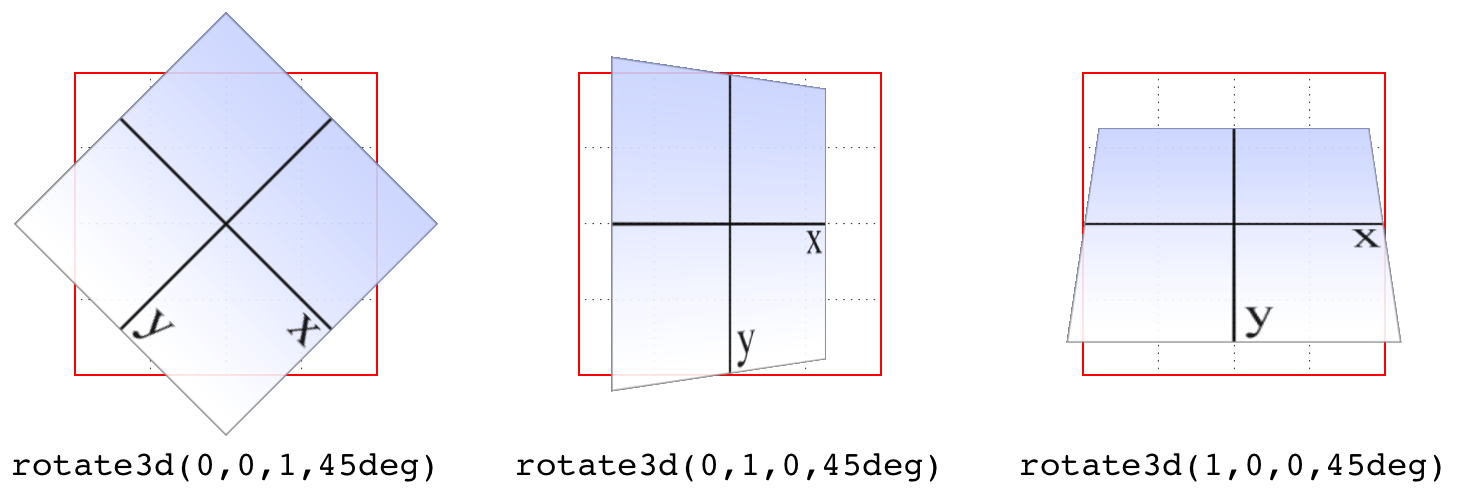
Figure 16-13. Rotations around 3D vectors
A little more complicated is something like
rotate3d(-0.95,0.5,1,45deg), where the described vector points off into 3D space between the axes. To understand how this works,
let’s start with a basic example: rotateZ(45deg) (illustrated in
Figure 16-13). The equivalent is rotate3d(0,0,1,45deg). The first three
numbers describe the components of a vector that has no x or y
magnitude, and a z magnitude of 1. Thus, it points along the z-axis in a
positive direction; that is, toward the viewer. The element is then
rotated clockwise as you look toward the origin of the vector.
Similarly, the 3D equivalent of rotateX(45deg) is
rotate3d(1,0,0,45deg). The vector points along the x-axis in the
positive direction (to the right). If you stand at the end of that vector
and look toward its origin, then you rotate the element 45 degrees
clockwise around the vector. Thus, from the usual viewer placement, the
top of the element rotates away from and the bottom rotates toward the
viewer.
Let’s make it slightly more complex: suppose you have
rotate3d(1,1,0,45deg). When viewed on your monitor, that describes a
vector running from the top-left to bottom-right corner, going right through
the center of the element (by default, anyway; we’ll see how to change
that later on). So the element’s rectangle has a line running through it
at a 45-degree angle, effectively spearing it. Then the vector rotates
45 degrees, taking the element with it. The rotation is clockwise as you
look back toward the vector’s origin, so again, the top of the element
rotates away from the viewer, while the bottom rotates toward the viewer. If we
were to change the rotation to rotate3d(1,1,0,90deg), then the element
would be edge-on to the viewer, tilted at a 45-degree angle and facing
off toward the upper right. Try it with a piece of paper: draw a line
from the top left to bottom right, and then rotate the paper around that
line.
OK, so given all that, try visualizing how the vector is determined
for rotate3d(-0.95,0.5,1,45deg). If we assume a cube 200 pixels on a
side, the vector’s components are 190 pixels to the left along the x-axis, 100 pixels down along the y-axis, and 200 pixels toward the views
along the z-axis. The vector goes from the origin point (0, 0, 0) to the point
(-190 px, 100 px, 200 px). Figure 16-14 depicts that vector, as well as the
final result presented to the viewer.
So the vector is like a metal rod speared through the element being rotated. As we look back along the line of the vector, the rotation is 45 degrees clockwise. But since the vector points left, down, and forward, that means the top-left corner of the element rotates toward the viewer, and the bottom right rotates away, as shown in Figure 16-14.
Just to be crystal clear, rotate3d(1,1,0,45deg) is not equivalent to
rotateX(45deg) rotateY(45deg) rotateZ(0deg)! It’s an easy mistake to
make, and many people—including several online tutorial authors and,
until researching and writing this section, your humble
correspondent—have made it. It seems like it should be equivalent, but it really
isn’t. If we place that vector inside the imaginary 200 × 200 × 200 cube
previously mentioned, the axis of rotation would go from the origin
point to a point 200 pixels right and 200 pixels down (200, 200, 0).
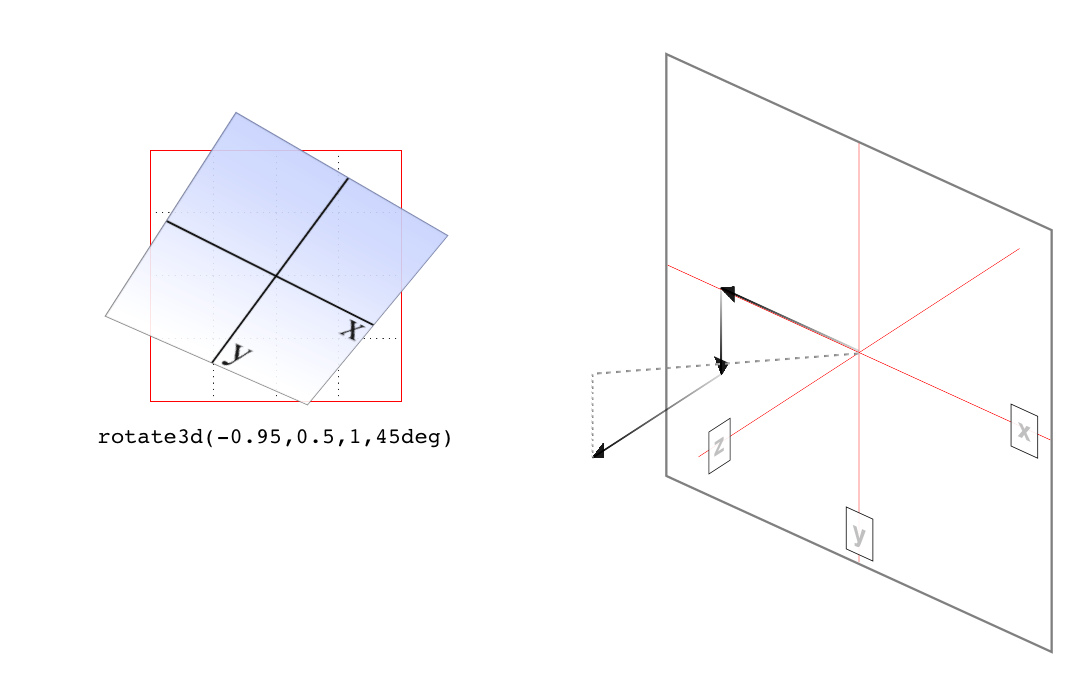
Figure 16-14. Rotation around a 3D vector, and how that vector is determined
Having done that, the axis of rotation is shooting through the element
from the top left to the bottom right, at a 45-degree angle. The element
then rotates 45 degrees clockwise around that diagonal, as you look back
toward its origin (the top left), which rotates the top-right corner of
the element away and a bit to the left, while the bottom-left corner
rotates closer and a bit to the right. This is distinctly different than
the result of rotateX(45deg) rotateY(45deg) rotateZ(0deg), as you can
see in Figure 16-15.
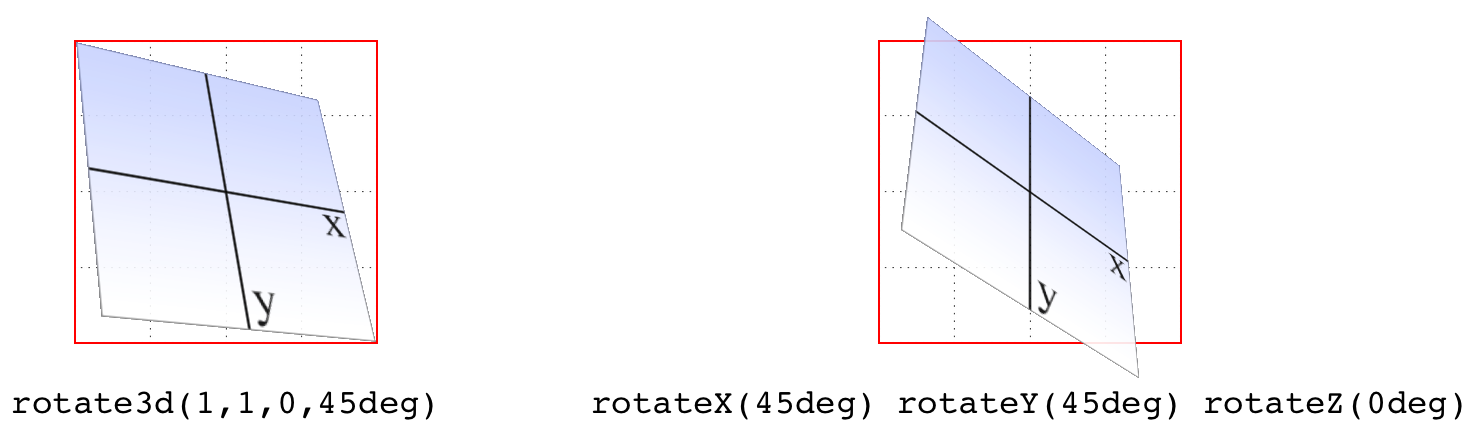
Figure 16-15. The difference between rotating around two axes and rotating around a 3D axis
Skew functions
When you skew an element, you slant it along one or both of the x- and y-axes. There is no z-axis or other 3D skewing.
| Functions | Permitted value |
|---|---|
|
<angle> |
In both cases, you supply an angle value, and the element is skewed to match that angle. It’s much easier to show skewing rather than try to explain it in words, so Figure 16-16 shows a number of skew examples along the x- and y-axes.
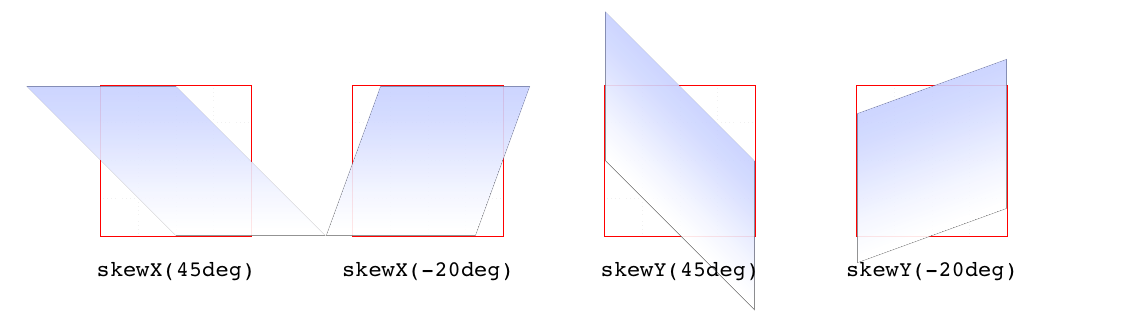
Figure 16-16. Skewing along the x- and y-axes
| Function | Permitted values |
|---|---|
|
<angle> [ |
The behavior of including skew(a,b) is different from including
skewX(a) with skewY(b). Instead, it specifies a 2D skew using the
matrix operation [ax,ay]. Figure 16-17 shows some examples of this matrix
skewing and how they differ from double-skew transforms that look the
same at first, but aren’t.
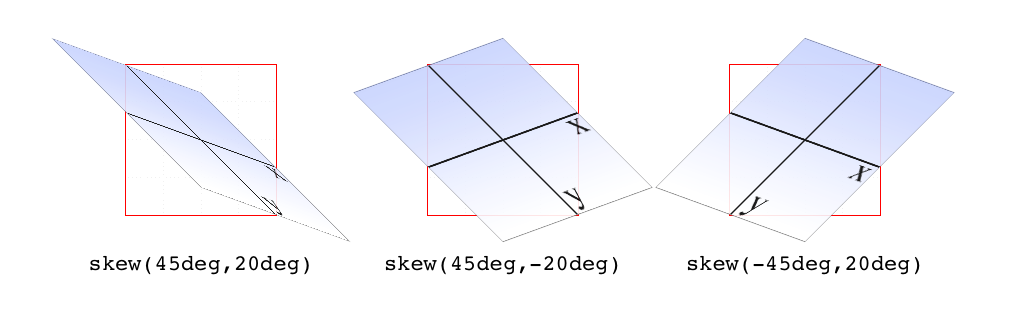
Figure 16-17. Skewed elements
If you supply two values, the x skew angle is always first, and the y skew angle comes second. If you leave out a y skew angle, then it’s treated as zero.
The perspective function
If you’re transforming an element in 3D space, you most likely want it to have some perspective. Perspective gives the appearance of front-to-back depth, and you can vary the amount of perspective applied to an element.
| Function | Permitted values |
|---|---|
|
<length> |
It might seem a bit weird that you specify perspective as a distance.
After all, perspective(200px) seems a bit odd when you can’t really
measure pixels along the z-axis. And yet, here we are. You supply a
length, and the illusion of depth is constructed around that value.
Lower numbers create more extreme perspective, as though you are right
up close to the element and viewing it through a fish-eye lens. Higher
numbers create a gentler perspective, as though viewing the element
through a zoom lens from far away. Really high perspective values
create an isometric effect.
This makes a certain amount of sense. If you visualize perspective as a pyramid, with its apex point at the perspective origin and its base the closest thing to you, then a shorter distance between apex and base will create a shallower pyramid, and thus a more extreme distortion. This is illustrated in Figure 16-18, with hypothetical pyramids representing 200 px, 800 px, and 2,000 px perspective distances.
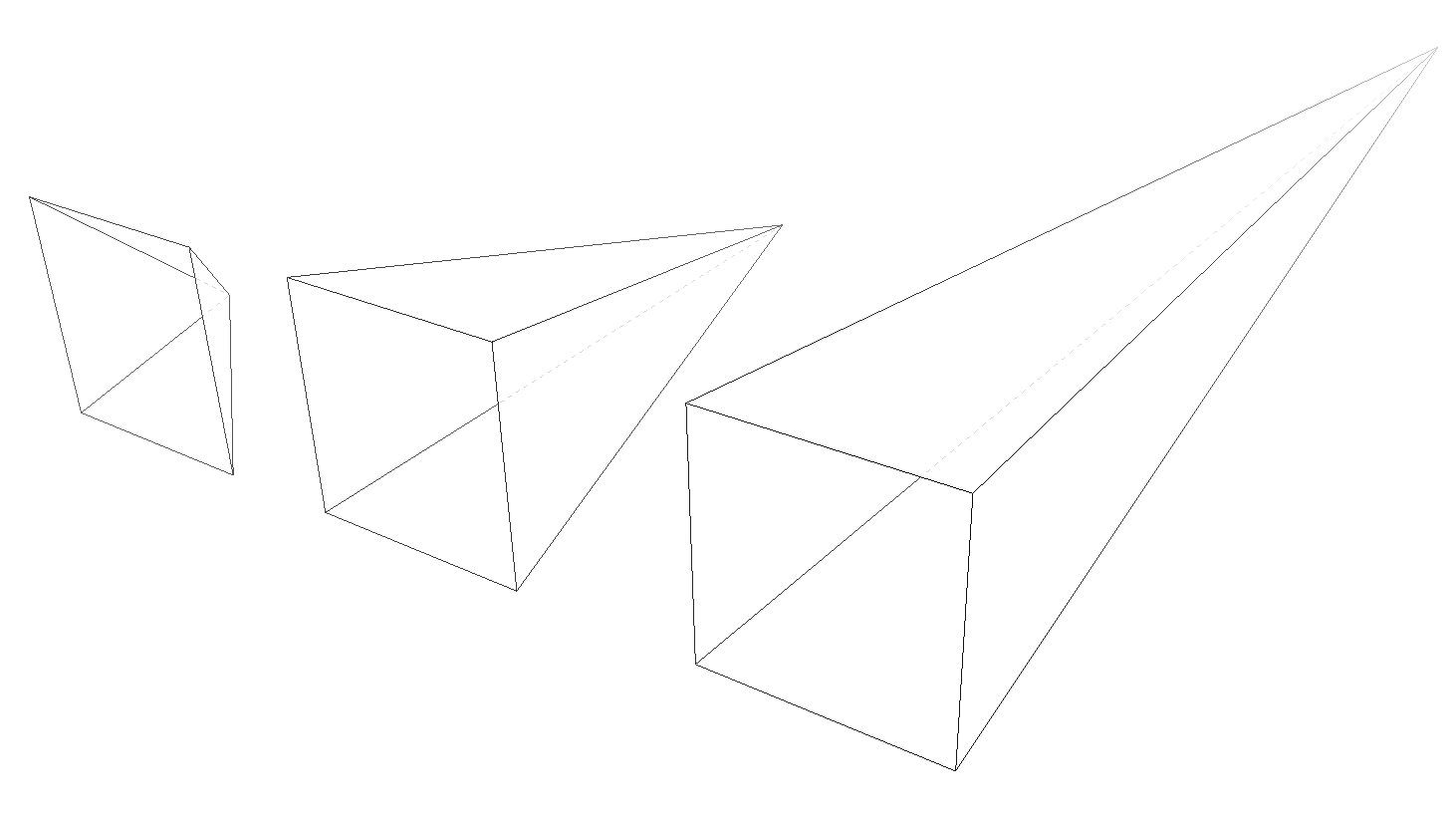
Figure 16-18. Different perspective pyramids
In the documentation for Safari, Apple writes that perspective values
below 300px tend to be extremely distorted, values above 2000px
create “very mild” distortion, and values between 500px and 1000px
create “moderate perspective.” To illustrate this, Figure 16-19 shows a series of elements with the exact same rotation as displayed with varying perspective values.
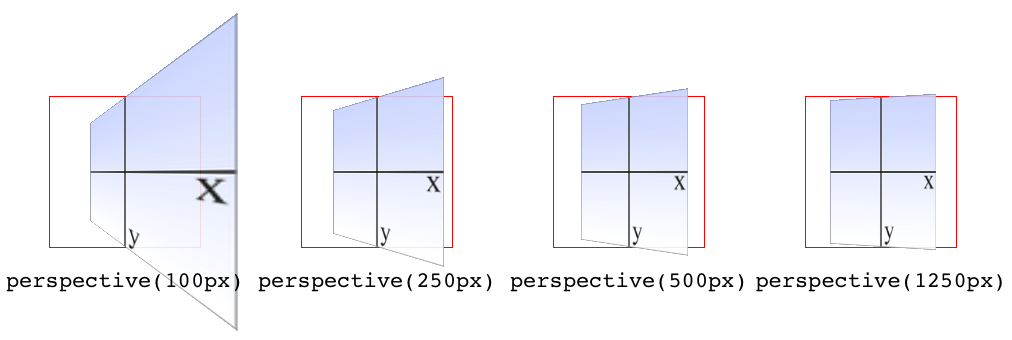
Figure 16-19. The effects of varying perspective values
Perspective values must always be positive, nonzero lengths. Any other
value will cause the perspective() function to be ignored. Also note
that its placement in the list of functions is very important. If you
look at the code for Figure 16-19, the perspective() function comes
before the rotateY() function. If you were to reverse the order, the
rotation would happen before the perspective is applied, so all four
examples in Figure 16-19 would look exactly the same. So if you plan to
apply a perspective value via the list of transform functions, make sure
it comes first, or at the very least before any transforms that depend
on it. This serves as a particularly stark reminder that the order in which you
write transform functions can be very important.
Matrix functions
If you’re a particular fan of advanced math, or stale jokes derived from the Wachowskis’ movies, then these functions will be your favorites.
| Function | Permitted values |
|---|---|
|
<number> [ |
In the CSS transforms specification, we find the trenchant description
of matrix() as a function that “specifies a 2D transformation in the
form of a transformation matrix of the six values a-f.”
First things first: a valid matrix() value is a list of six
comma-separated numbers. No more, no less. The values can be positive or
negative. Second, the value describes the final transformed state of the
element, combining all of the other transform types (rotation, skewing,
and so on) into a very compact syntax. Third, very few people actually use
this syntax.
We’re not actually going to go through the complicated process of actually doing the matrix math. For most readers, it would be an eye-watering wall of apparent gibberish; and for the rest, it would be time wasted on familiar territory. You can certainly research the intricacies of matrix calculations online, and I encourage anyone with an interest to do so. We’ll just look at the basics of syntax and usage in CSS.
Here’s a brief rundown of how it works. Say you have this function applied to an element:
matrix(0.838671,0.544639,-0.692519,0.742636,6.51212,34.0381)
That’s the CSS syntax used to describe this transformation matrix:
0.838671-0.69251906.512120.5446390.742636034.038100100001
Right. So what does that do? It has the result shown in Figure 16-20, which is exactly the same result as writing this:
rotate(33deg)translate(24px,25px)skewX(-10deg)
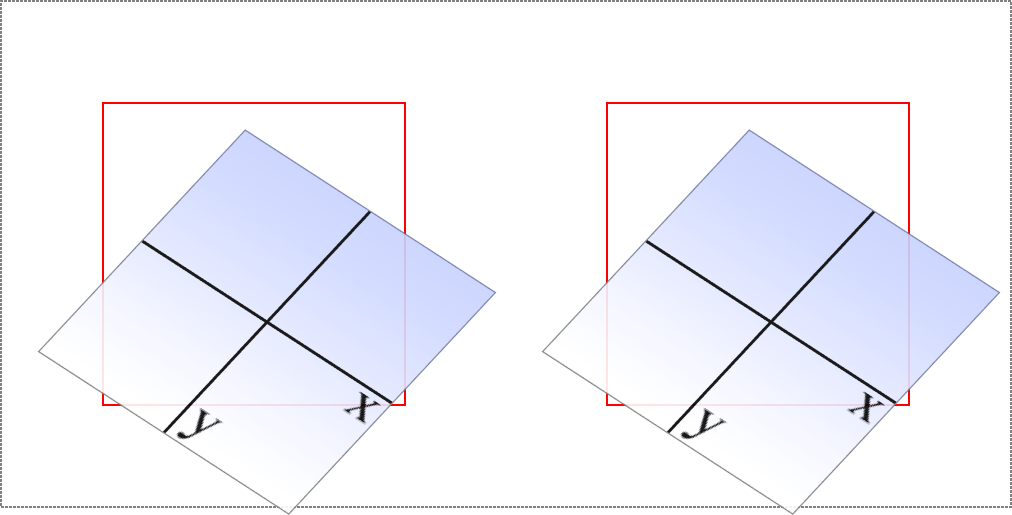
Figure 16-20. A matrix-transformed element and its functional equivalent
What this comes down to is that if you’re familiar with or need to make use of matrix calculations, you can and should absolutely use them. If not, you can chain much more human-readable transform functions together and get the element to the same end state.
Now, that was for plain old 2D transforms. What if you want to use a matrix to transform through three dimensions?
| Function | Permitted values |
|---|---|
|
<number> |
Again, just for kicks, we’ll savor the definition of matrix3d() from
the CSS Transforms specification: “specifies a 3D transformation as a
4 × 4 homogeneous matrix of 16 values in column-major order.” This means
the value of matrix3d must be a list of 16 comma-separated numbers,
no more or less. Those numbers are arranged in a 4 × 4 grid in column
order, so the first column of the matrix is formed by the first set of
four numbers in the value, the second column by the second set of four
numbers, the third column by the third set, and so on. Thus, you can
take the following function:
matrix3d(0.838671,0,-0.544639,0.00108928,-0.14788,1,0.0960346,-0.000192069,0.544639,0,0.838671,-0.00167734,20.1281,25,-13.0713,1.02614)
And write it out as this matrix:
0.838671-0.147880.54463920.128101025-0.5446390.09603460.838671-13.07130.00108928-0.000192069-0.001677341.02614
Both of which have an end state equivalent to:
perspective(500px)rotateY(33deg)translate(24px,25px)skewX(-10deg)
as shown in Figure 16-21.
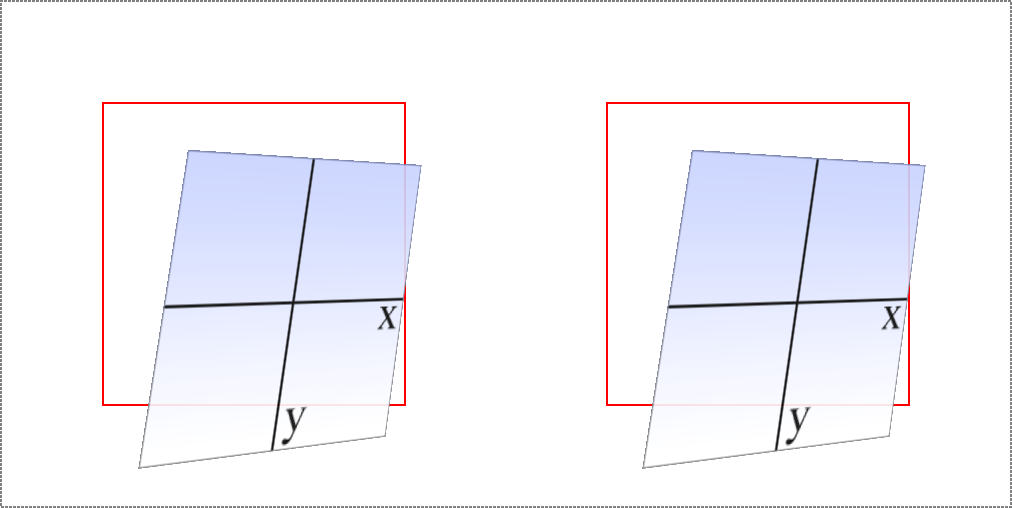
Figure 16-21. A matrix3d-transformed element and its functional equivalent
A note on end-state equivalence
It’s important to keep in mind that only the end states of a matrix()
function, and of an equivalent chain of transform functions, can be
considered identical. This is for the same reason discussed in
the section on rotation: because a rotation angle of 393deg will end
with the same visible rotation as an angle of 33deg. This matters if
you are animating the transformation, since the former will cause the
element to do a barrel roll in the animation, whereas the latter will
not. The matrix() version of this end state won’t include the barrel
roll, either. Instead, it will always use the shortest possible rotation
to reach the end state.
To illustrate what this means, consider the following: a transform chain
and its matrix() equivalent:
rotate(200deg)translate(24px,25px)skewX(-10deg)matrix(-0.939693,-0.34202,0.507713,-0.879385,-14.0021,-31.7008)
Note the rotation of 200 degrees. We naturally interpret this to mean a
clockwise rotation of 200 degrees, which it does. If these two
transforms are animated, however, they will have act differently: the
chained-functions version will indeed rotate 200 degrees clockwise,
whereas the matrix() version will rotate 160 degrees counterclockwise.
Both will end up in the same place, but will get there in different
ways.
There are similar differences that arise even when you might think they
wouldn’t. Once again, this is because a matrix() transformation will
always take the shortest possible route to the end state, whereas a
transform chain might not. (In fact, it probably doesn’t.) Consider
these apparently equivalent transforms:
rotate(160deg)translate(24px,25px)rotate(-30deg)translate(-100px)matrix(-0.642788,0.766044,-0.766044,-0.642788,33.1756,-91.8883)
As ever, they end up in the same place. When animated, though, the elements will take different paths to reach that end state. They might not be obviously different at first glance, but the difference is still there.
None of this matters if you aren’t animating the transformation, but it’s an important distinction to make nevertheless, because you never know when you’ll decide to start animating things. (Hopefully after reading the companion text on animations!)
More Transform Properties
In addition to the base transform property, there are a few related
properties that help to define things such as the origin point of a
transform, the perspective used for a “scene,” and more.
Moving the Origin
So far, all of the transforms we’ve seen have shared one thing in
common: the precise center of the element was used as the transform
origin. For example, when rotating the element, it rotated around its
center, instead of, say, a corner. This is the default behavior, but
with the property transform-origin, you can change it.
The syntax definition looks really abstruse and confusing, but it’s actually
fairly simple in practice. With transform-origin, you supply two or three keywords to define the point
around which transforms should be made: first the horizontal, then the
vertical, and optionally a length along the z-axis. For the horizontal and vertical axes,
you can use plain-English keywords like top and right,
percentages, lengths, or a combination of different keyword types.
For the z-axis, you can’t use plain-English keywords or percentages,
but can use any length value. Pixels are by far the most common.
Length values are taken as a distance starting from the top-left corner of the
element. Thus, transform-origin: 5em 22px will place the transform
origin 5 em to the right of the left side of the element, and 22 pixels
down from the top of the element. Similarly, transform-origin:
5em 22px -200px will place it 5 em over, 22 pixels down, and 200 pixels
away; that is, 200 pixels behind the place where the element sits.
Percentages are calculated with respect to the corresponding axis and
size of the element, as offsets from the element’s top-left corner. For
example, transform-origin: 67% 40% will place the transform origin 67
percent of the width to the right of the element’s left side, and 40
percent of the element’s height down from the element’s top side. Figure 16-22 illustrates a few origin calculations.
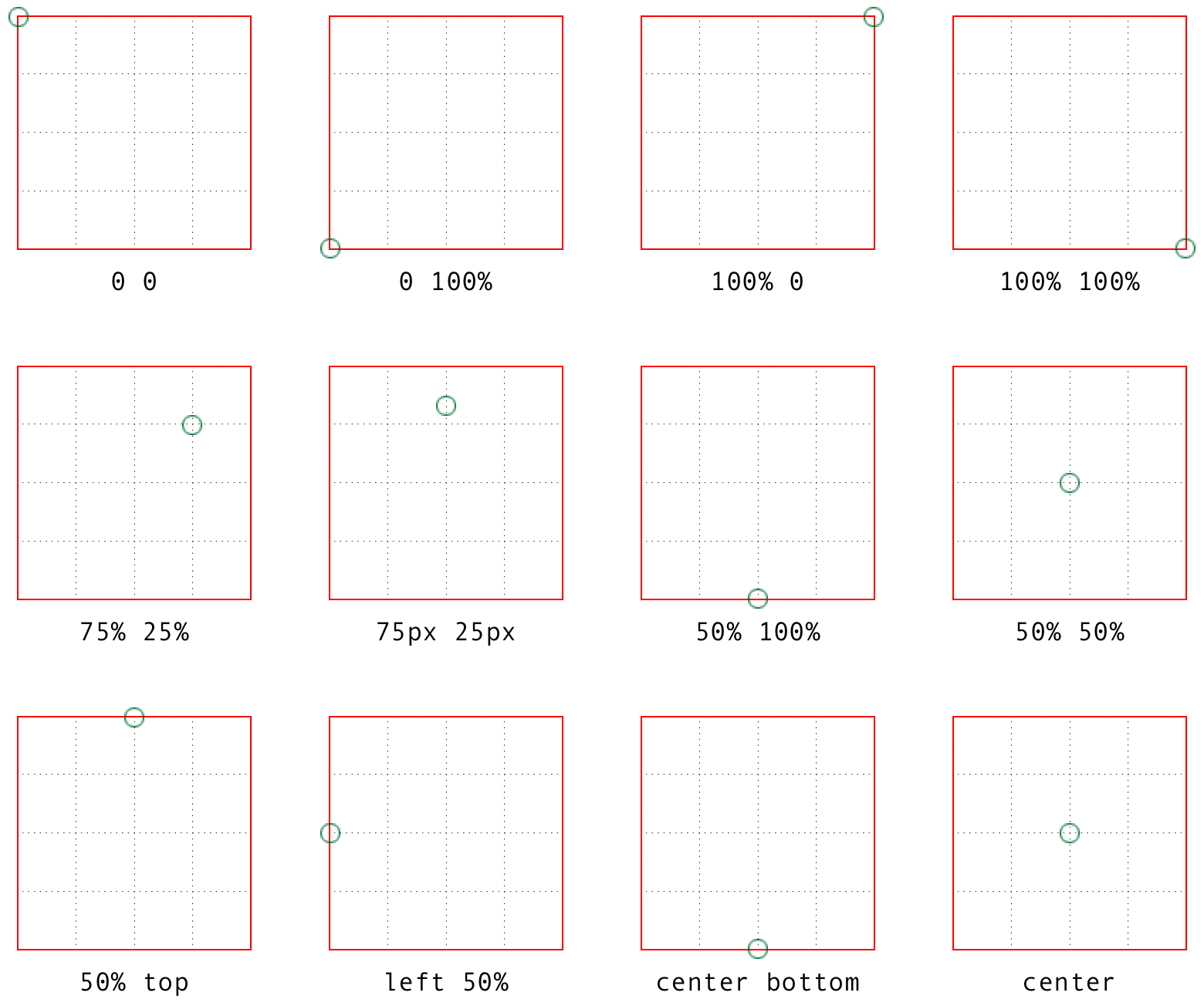
Figure 16-22. Various origin calculations
All right, so if you change the origin, what happens? The easiest way to visualize this is with 2D rotations. Suppose you rotate an element 45 degrees to the right. Its final placement will depend on its origin. Figure 16-23 illustrates the the effects of several different transform origins; in each case, the transform origin is marked with a circle.
The origin matters for other transform types, such as skews and scales. Scaling an element with its origin in the center will pull in all sides equally, whereas scaling an element with a bottom-right origin will cause it to shrink toward that corner. Similarly, skewing an element with respect to its center will result in the same shape as if it’s skewed with respect to the top-right corner, but the placement of the shape will be different. Some examples are shown in Figure 16-24; again, each transform origin is marked with a circle.
The one transform type that isn’t really affected by changing the
transform origin is translation. If you push an element around with
translate(), or its cousins like translateX() and translateY(),
it’s going to end up in the same place regardless of where the transform
origin is located. If that’s all the transforming you plan to do, then
setting the transform origin is irrelevant. If you ever do anything
besides translating, though, the origin will matter. Use it wisely.

Figure 16-23. The rotational effects of using various transform origins

Figure 16-24. The skew effects of using various transform origins
Choosing a 3D Style
If you’re setting elements to be transformed through three
dimensions—using, say, translate3d() or rotateY()—you probably
expect that the elements will be presented as though they’re in a 3D
space. And yet, this is not the default behavior. By default, everything
looks flat no matter what you do. Fortunately, this can be overridden
with the transform-style property.
Suppose you have an element you want to move “closer to” your eye, and then tilt away a bit, with a moderate amount of perspective. Something like this rule, as applied to the following HTML:
div#inner{transform:perspective(750px)translateZ(60px)rotateX(45deg);}<divid="outer">outer<divid="inner">inner</div></div>
So you do that, and get the result shown in Figure 16-25; more or less what you might have expected.
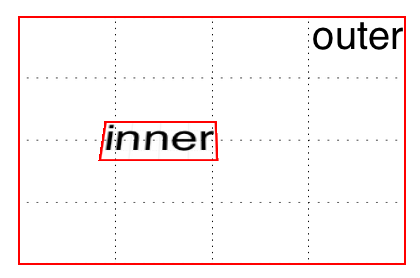
Figure 16-25. A 3D-transformed inner div
But then you decide to rotate the outer div to one side, and suddenly
nothing makes sense any more. The inner div isn’t where you envisioned
it. In fact, it just looks like a picture pasted to the front of the
outer div.
Well, that’s exactly what it is, because the default value of
transform-style is flat. The inner div got
drawn in its moved-forward-tilted-back state, and that was applied to
the front of the outer div as if it was an image. So when you rotated
the outer div, the flat picture rotated right along with it, as shown
in Figure 16-26:
div#outer{transform:perspective(750px)rotateY(60deg)rotateX(-20deg);}div#inner{transform:perspective(750px)translateZ(60px)rotateX(45deg);}
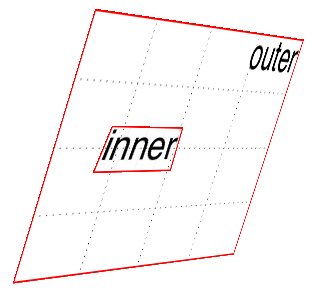
Figure 16-26. The effects of a flat transform style
Change the value to preserve-3d, however, and things are suddenly different.
The inner div will be drawn as a full 3D object with respect to its
parent outer div, floating in space nearby, and not as a picture
pasted on the front of the outer div. You can see the results of this
change in Figure 16-27:
div#outer{transform:perspective(750px)rotateY(60deg)rotateX(-20deg);transform-style:preserve-3d;}div#inner{transform:perspective(750px)translateZ(60px)rotateX(45deg);}
One important aspect of transform-style is that it can be overridden
by other properties. The reason is that some values of these other
properties require a flattened presentation of an element and its
children in order to work at all. In such cases, the value of
transform-style is forced to be flat, regardless of what you may
have declared.
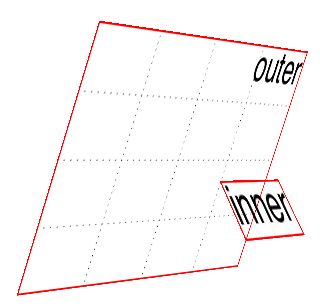
Figure 16-27. The effects of a 3D-preserved transform style
So, in order to avoid this overriding behavior, make sure the following properties are set to the listed values:
-
overflow: visible -
filter: none -
clip: auto -
clip-path: none -
mask-image: none -
mask-border-source: none -
mix-blend-mode: normal
Those are all the default values for those properties, so as long as you don’t try to change any of them for your preserved 3D elements, you’re fine! But if you find that editing some CSS suddenly flattens out your lovely 3D transforms, one of these properties might be the culprit.
One more note: in addition to the values just mentioned, the value of the property isolation must be, or be computed to be, isolate. (isolation is a compositing property, in case you were wondering.)
Changing Perspective
There are actually two properties that are used to define how
perspective is handled: one to define the perspective distance, as with
the perspective() function discussed in an earlier section; and
another to define the perspective’s origin point.
Defining a group perspective
First, let’s consider the property perspective, which accepts a length
that defines the depth of the perspective pyramid. At first glance, it
looks just like the perspective() function discussed earlier, but
there are some critical differences.
As a quick example, if you want to create a very deep perspective, one
mimicking the results you’d get from a zoom lens, you might declare
something like perspective: 2500px. For a shallow depth, one that
mimics a closeup fish-eye lens effect, you might declare perspective: 200px.
So how does this differ from the perspective() function? When you use
perspective(), you’re defining the perspective effect for the element
that is given that function. So if you say
transform: perspective(800px) rotateY(-50grad);, you’re applying that
perspective to each element that has the rule applied.
With the perspective property, on the other hand, you’re creating a
perspective depth that is applied to all the child elements of the
element that received the property. Confused yet? Don’t be. Here’s an illustration of the difference, as shown in Figure 16-28:
div{transform-style:preserve-3d;border:1pxsolidgray;width:660px;}img{margin:10px;}#one{perspective:none;}#oneimg{transform:perspective(800px)rotateX(-50grad);}#two{perspective:800px;}#twoimg{transform:rotateX(-50grad);}<div><imgsrc="rsq.gif"><imgsrc="rsq.gif"><imgsrc="rsq.gif"></div><divid="one"><imgsrc="rsq.gif"><imgsrc="rsq.gif"><imgsrc="rsq.gif"></div><divid="two"><imgsrc="rsq.gif"><imgsrc="rsq.gif"><imgsrc="rsq.gif"></div>

Figure 16-28. Shared perspective versus individual perspectives
In Figure 16-28, we first see a line of images that haven’t been transformed. In the second line, each image has been rotated 50 gradians (equivalent to 45 degrees) toward us, but each one within its own individual perspective.
In the third line of images, none of them has an individual perspective.
Instead, they are all drawn within the perspective defined by
perspective: 800px; that’s been set on the div that contains them.
Since they all operate within a shared perspective, they look “correct”;
that is, like we would expect if we had three physical pictures mounted
on a clear sheet of glass and rotated toward us around the center
horizontal axis of that glass.
Note
Note that presence of transform-style: preserve-3d makes this effect
possible, as discussed in the previous section.
This is the critical difference between perspective, the property; and
perspective(), the function. The former creates a 3D space shared by
all its children. The latter affects only the element to which it’s
applied. A less important difference is that the perspective()
function has to come first or early in its chain of transforms in order
to apply to the element as it’s transformed through 3D space. The
perspective property, on the other hand, is applied to all children,
regardless of where their transforms are declared.
In most cases, you’re going to use the perspective property instead of
the perspective() function. In fact, container divs (or other
elements) are a very common feature of 3D transforms—the way they used
to be for page layout—largely to establish a shared perspective. In the
previous example, the <div id="two"> was there solely to serve as a
perspective container, so to speak. On the other hand, we couldn’t have
done what we did without it.
Moving the perspective’s origin
When transforming elements in three dimensions—assuming you’ve allowed
them to appear three-dimensional, that is—a perspective will be used. (See transform-style and perspective, respectively, in
previous sections.) That perspective will have an origin, which is also
known as the vanishing point, and you can change where it’s located
with the property perspective-origin.
As you may have spotted, perspective-origin and transform-origin have the same value syntax, right down to allowing
an optional length value defining an offset along the z-axis. While the way the values
are expressed is identical, the effects they have are very different.
With transform-origin, you define the point around which transforms
happen. With perspective-origin, you define the point on which sight
lines converge.
As with most 3D transform properties, this is more easily demonstrated than described. Consider the following CSS and markup, illustrated in Figure 16-29:
#container{perspective:850px;perspective-origin:50%0%;}#ruler{height:50px;background:#DEDurl(tick.gif)repeat-x;transform:rotateX(60deg);transform-origin:50%100%;}<divid="container"><divid="ruler"></div></div>

Figure 16-29. A basic “ruler”
What we have is a repeated background image of tick-marks on a ruler,
with the div that contains them tiled away from us by 60 degrees. All
the lines point at a common vanishing point, the top center of the
container div (because of the 50% 0% value for
perspective-origin).
Now consider that same setup with various perspective origins, as shown in Figure 16-30.

Figure 16-30. A basic “ruler” with different perspective origins
As you can see, moving the perspective origin changes the rendering of the 3D-transformed element.
Note that these only had an effect because we supplied a value for
perspective. If the value of perspective is ever the default none,
then any value given for perspective-origin will be ignored. That
makes sense, since you can’t have a perspective origin when there’s no
perspective at all!
Dealing with Backfaces
Something you probably never really thought about, over all the years
you’ve been laying out elements, was: what would it look like if I could
see the back side of the element? Now that 3D transforms are a
possibility, there may well come a day when you do see the back side of
an element. You might even mean to do so intentionally. What happens at
that moment is determined by the property backface-visibility.
Unlike many of the other properties and functions we’ve already talked about, this one is pretty uncomplicated. All it does is determine whether the back side of an element is rendered when it’s facing toward the viewer, or not. That’s it.
So let’s say you flip over two elements, one with backface-visibility
set to the default value of visible and the other set to hidden. You
get the result shown in Figure 16-31:
span{border:1pxsolidred;display:inline-block;}img{vertical-align:bottom;}img.flip{transform:rotateX(180deg);display:inline-block;}img#show{backface-visibility:visible;}img#hide{backface-visibility:hidden;}<span><imgsrc="salmon.gif"></span><span><imgsrc="salmon.gif"class="flip"id="show"></span><span><imgsrc="salmon.gif"class="flip"id="hide"></span>

Figure 16-31. Visible and hidden backfaces
As you can see, the first image is unchanged. The second is flipped over around its x-axis, so we see it from the back. The third has also been flipped, but we can’t see it at all because its backface has been hidden.
This property can come in handy in a number of situations. The simplest is a case where you have two elements that represent the two sides of a UI element that flips over; say, a search area with preference settings on its back, or a photo with some information on the back. Let’s take the latter case. The CSS and markup might look something like this:
section{position:relative;}img,div{position:absolute;top:0;left:0;backface-visibility:hidden;}div{transform:rotateY(180deg);}section:hover{transform:rotateY(180deg);transform-style:preserve-3d;}<section><imgsrc="photo.jpg"alt=""><divclass="info">(…infogoeshere…)</div></section>
Actually, this example shows that using backface-visibility isn’t
quite as simple as it first appears. It’s not that the property itself
is complicated, but if you forget to set transform-style to
preserve-3d, then it won’t work as intended. That’s why
transform-style is set on the section element.
There’s a variant of this example that uses the same markup, but a slightly different CSS to show the image’s backface when it’s flipped over. This is probably more what was intended, since it makes information look like it’s literally written on the back of the image. It leads to the end result shown in Figure 16-32:
section{position:relative;}img,div{position:absolute;top:0;left:0;}div{transform:rotateY(180deg);backface-visibility:hidden;background:rgba(255,255,255,0.85);}section:hover{transform:rotateY(180deg);transform-style:preserve-3d;}

Figure 16-32. Photo on the front, information on the back
The only thing we had to do to make that happen was to just shift the
backface-visibilty: hidden to the div instead of applying it to both
the img and the div. Thus, the div’s backface is hidden when it’s
flipped over, but that of the image is not.
Summary
With the ability to transform elements in two- and three-dimensional space, CSS transforms provide a great deal of power to designers who are looking for new ways to present information. From creating interesting combinations of 2D transforms, to creating a fully 3D-acting interface, transforms open up a great deal of new territory in the design space. There are some interesting dependencies between properties, which is something that not every CSS author will find natural at first, but they become second nature with just a bit of practice.