1. Vlad is shopping for a new shirt because all the stores are having end-of-season sales. Sam’s Special Shirts offers Vlad 20% off all his purchases while Hardworking Harry’s Haberdashery has a special sale offering five shirts for the price of four. Which is the better deal?
(A) neither
(B) Sam’s Special Shirts
(C) both are the same
(D) Hardworking Harry’s Haberdashery
2. Olga designed a logo consisting of an equilateral triangle in a circle for a new company. She designed it with one vertex of the triangle pointing northeast. The client said she liked the design but preferred that the vertex of the triangle point due south. What rotation would Olga have to perform to satisfy her client?
(A) 90 degrees to the right
(B) 110 degrees to the right
(C) 135 degrees to the left
(D) 135 degrees to the right
3. Solve the following equation for x:
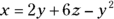, if 
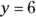and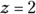 
(A) 12
(B) 11
(C) –12
(D) –11
Question 4 refers to the following table.
|
Make and Model |
Price |
|
Hopper Model A1 |
$249.99 |
|
Vacuous Vacuum Company Model ZZ3 |
$679.99 |
|
Clean-R-Up Special Series |
$179.00 |
|
Electrified Home Upright |
$749.99 |
|
Super Suction 101 |
$568.99 |
4. Pierre is looking for a vacuum cleaner for his apartment. He is on a limited budget and wants to spend the least he can for his purchase. He has been told by his best friend that spending around the mean amount for a vacuum cleaner will get him an average unit. His father claims that spending about the median amount is the smartest way to get a good deal. 
comes the closest to satisfying both criteria.
5. Evaluate the following formula to two decimal places:
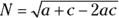, if 
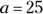and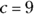 
(A) 34.67
(B) 20.40
(C) 22.47
(D) no answer
6. Solve the following equation for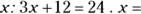 
(A) 12
(B) 3
(C) 4
(D) 5
7. Rachel and Ronda were planning for their first apartment, and they decided to split the required shopping tasks. Rachel was responsible for finding out how much it would cost to carpet their living room, and Ronda was responsible for finding out how much it would cost to paint the walls in the bedroom. What formula would each of them need to use to get an answer that would let them figure out the price for each job?
(A)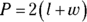 
(B)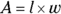 
(C)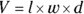 
(D)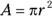 
8. Lillian is drawing a scale diagram of her apartment to take with her while shopping for rugs. If she has taken all the measurements in the apartment, what mathematical relationship would she use to draw the scale drawing?
(A) decimals
(B) exponents
(C) ratios
(D) addition
9. Sylvia couldn’t fall asleep one night and got to wondering how much water her bedroom would hold if she filled it to the ceiling. She had previously measured all the walls and knew all the measurements, including length, width, and height. She should use to calculate how many cubic feet of water would be needed to fill the room.
10. Alvin is drawing a diagram of his room. He has drawn the line representing the floor and is ready to draw the line representing the wall. This line would be ________ to the line representing the floor.
(A) congruent
(B) parallel
(C) similar
(D) perpendicular
11. Aaron wants to paint the floor of his apartment. His living room/dining room is 19 feet by 16 feet, his bedroom is 12 feet by 14 feet, and his hallways are 6 feet by 8 feet. Bowing to pressure from his friends, he has decided not to paint the floor of the kitchen or the bathroom. How many square feet of floor must he paint?
(A) 304
(B) 520
(C) 250
(D) 216
Question 12 refers to the following table.
|
Week |
Calories Consumed Per Week |
Weight (Pounds) |
Height (Feet/Inches) |
|
1 |
12,250 |
125 |
5 ft. 1.5 in. |
|
2 |
15,375 |
128 |
5 ft. 1.5 in. |
|
3 |
13,485 |
128 |
5 ft. 1.5 in. |
|
4 |
16,580 |
130 |
5 ft. 1.5 in. |
|
5 |
15,285 |
129 |
5 ft. 1.5 in. |
12. Alan kept track of his caloric intake, his weight, and his height for a period of five weeks. What conclusion can you draw from his observations?
(A) Eating a lot makes you taller.
(B) Eating more calories will make you gain weight.
(C) Gaining weight will make you taller.
(D) There’s no correlation between the data presented.
13. On Monday, Mary walked 12 blocks. On Tuesday, she walked 10 blocks, and on Wednesday, she walked 14 blocks. If she wants to walk more than her average trip for those three days on Thursday, at least how many blocks must she walk?
(A) 10
(B) 11
(C) 9
(D) 13
14. Hassan has developed a new trick to play on his classmates. He asks them to write down their ages and multiply by 4, divide by 2, then subtract 6, and, finally, add 8. When they tell him the resulting number, Hassan can always tell them their age. If one of his friends tells Hassan the resultant number is 52, how old is he?
(A) 33
(B) 25
(C) 52
(D) 24
Question 15 refers to the following table.
|
a |
b |
F |
|
1 |
2 |
–16 |
|
2 |
1 |
–3 |
|
3 |
2 |
–18 |
|
2 |
3 |
–35 |
|
3 |
4 |
x |
15. Herman developed the following function to amuse himself: F = 2a + 3b2 – 2ab. He kept track of his results in this table.
Using Herman’s function, what is the value of x?
(A) 53
(B) -82
(C) 88
(D) 30
16. Calvin and Kelvin, carpenters extraordinaire, are building a staircase for their clients, the Coalmans. The stairway is to bridge a space 10 feet high, and the distance from the front of the bottom step to the back of the top step is 14 feet. What is the slope of the stairway to 2 decimal places?
(A) 0.69
(B) 0.70
(C) 0.71
(D) 0.72
Questions 17 and 18 refer to the following information.
April is considering two apartments. They are of equal size except for the bedrooms. Bedroom A is 19 feet by 14 feet, and bedroom B is 17 feet by 16 feet.
17. How many square feet larger is the larger bedroom?
(A) 8
(B) 7
(C) 6
(D) 5
18. April wants an area rug for the larger bedroom that would cover the floor, leaving a space 1 foot from each wall. If the rug had a 1-inch fringe all the way around it, how many feet long would the fringe be?
(A) 58
(B) 29
(C) 85
(D) 55
Questions 19 and 20 refer to the following table, which shows the results Julio got from measuring and interviewing several of his classmates about their heights and birth months.
|
Month of Birth |
Height |
|
March |
5 ft. 4 in. |
|
June |
5 ft. 6 in. |
|
March |
5 ft. 1 in. |
|
January |
5 ft. 8 in. |
|
August |
5 ft. 5 in. |
|
January |
5 ft. 6 in. |
19. What month would produce the shortest people according to these measurements?
(A) January
(B) March
(C) June
(D) August
20. From the graph of Julio’s results, what conclusion, if any, can be reached?
(A) No conclusions can be reached.
(B) People born in March are shorter.
(C) People born in the warm months are similar in height.
(D) Two of Julio’s classmates were born in each of January and March.
21. Susie is shopping for a few groceries. She buys a loaf of bread for $1.29 and a half gallon of milk for $1.47. She sees her favorite cheese on sale for $2.07. If she has $5.00 in her purse, can she buy the cheese if there is no tax on food?
(A) unsure
(B) yes
(C) not enough money
(D) not enough information
Question 22 refers to the following table.
Annual Production of the Wonderful World of Widgets
|
Year |
Annual Production (In Million Units) |
|
2013 |
43 |
|
2012 |
29 |
|
2011 |
72 |
|
2010 |
70 |
|
2009 |
71 |
22. The general manager of the Wonderful World of Widgets wants to present these figures in a visual, easily understood way to the board of directors to help them understand the effect that the downturn in the economy is having on the production of widgets. What would be the best way to present the figures?
(A) a graph
(B) a series of tables
(C) verbal descriptions
(D) a movie of how widgets are used in America
23. Mark the points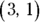 
, 
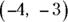, and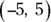 
on the graph to draw a geometric figure, and identify the figure.
© John Wiley & Sons, Inc.
24. Georgio wants to climb a ladder perched beside his house to check the condition of the eaves, which are 22 feet above the ground. For safety, the ladder should be placed 10 feet from the house. The minimum length of ladder he would need to reach the eaves, rounded up to the nearest foot, would be feet.
25. Where are all the points with an x-coordinate of –4 located on a graph?
(A) 4 units above the x-axis
(B) 4 units to the left of the x-axis
(C) 4 units above the y-axis
(D) 4 units to the left of the y-axis
Question 26 refers to the following table.
Age at Marriage for Those Who Retire at 55 in America
|
Age |
Women |
Men |
|
Under 20 years old |
27.6% |
11.7% |
|
20 to 24 years old |
36.6% |
38.8% |
|
25 to 29 years old |
16.4% |
22.3% |
|
30 to 34 years old |
8.5% |
11.6% |
|
35 to 39 years old |
5.1% |
6.5% |
26. Which of the following must be true, based on the information in this table, in order to ensure retirement at age 55?
(A) Younger women who want to retire at 55 should marry older men.
(B) More men who marry when they are under 20 years old are more likely retire at age 55 than those who marry when they are over 40 years old.
(C) To increase their odds of retirement at age 55, men should marry women who are the same age as they are.
(D) You can’t draw any of these conclusions from this table.
27. The students in a math class are looking at the equation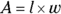 
. The teacher asks what result doubling the length (l) would have on the area (A). What answer is correct?
(A) makes it two times larger
(B) makes it four times larger
(C) makes it three times larger
(D) can’t determine the result without the value of w
28. A wall is 20 feet long and 8 feet high. If all of it is to be painted with two coats of blue paint, how many square feet of wall have to be covered?
(A) 56
(B) 160
(C) 230
(D) 320
29. Where on a graph would the point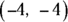 
be?
(A) four units to the right and four units below the corresponding axis
(B) four units to the left and four units below the corresponding axis
(C) four units to the left and four units above the corresponding axis
(D) four units to the right and four units above the corresponding axis
30. Roger and Ekua went shopping together. Ekua spent twice as much for clothing as Roger did. If their total expenditure for clothing was $90.00, how much did Roger spend for clothing?$
Question 31 refers to the following table.
|
Subject |
Height |
Shoe Size |
|
1 |
5 in. 3 ft. |
5 |
|
2 |
5 in. 9 ft. |
8 |
|
3 |
5 in. 6 ft. |
5½ |
|
4 |
6 in. 1 ft. |
10 |
|
5 |
5 in. 7 ft. |
6 |
31. Althea has a theory about the men in her class. She has decided that the taller men have larger shoe sizes than the shorter men. To prove her theory, she asked several of the men to measure themselves and tell her their shoe sizes. From her observations, she created the preceding table.
Using her observations, Althea decided to see whether there’s any credibility to her theory. If she calculated the median height of her subjects, what would be the corresponding shoe size?
(A) 5
(B) 6
(C) 8
(D) 10
32. Felix and Francis have just bought new cars. Felix, being American, has a car with a speedometer graduated in customary units. Francis, being Canadian, has a speedometer graduated in metric units. When they’re driving in Felix’s car at a speed of 55 miles per hour and if 1 mile equals approximately 1.6 kilometers, what would Francis’s speedometer read in kilometers per hour (rounded to the nearest number)?
(A) 160
(B) 88
(C) 55
(D) 77
33. The reading on the illustrated meter is .
© John Wiley & Sons, Inc.
Question 34 refers to the following table, which shows Sheila’s marks in her final year of high school.
|
Subject |
Grade (%) |
|
Literature |
94 |
|
Mathematics |
88 |
|
Physical Education |
86 |
|
Science |
92 |
|
Spanish |
90 |
34. The result on Sheila’s mean grade after a 6-point drop in her Spanish grade would be .
35. Barry earns $1,730 per month after taxes. Each month, he spends $900 for rent and $600 for living expenses like food and utilities. After all his expenses are paid, he has $ left over to buy luxuries and spend on entertainment.
Questions 36 and 37 refer to the following table.
|
Car Manufacturer |
Sales — July 2013 (In Thousands) |
Sales — July 2012 (In Thousands) |
% Change |
|
Commonwealth |
90 |
105 |
–14 |
|
Frisky |
175 |
147 |
+19 |
|
Goodenough |
236 |
304 |
–22 |
|
Horsesgalore |
99 |
64 |
+55 |
|
Silkyride |
24 |
16 |
+50 |
36. From the table, which car manufacturer showed the greatest percentage increase in sales?
(A) Commonwealth
(B) Frisky
(C) Goodenough
(D) Horsesgalore
37. From the table, which of the following conclusions could be drawn from the data?
(A) Car sales are increasing across the board.
(B) Car sales are decreasing across the board.
(C) Large manufacturers are selling more cars.
(D) No generalization is possible from this data.
Question 38 refers to the following table.
|
Person Interviewed |
Flavor Preference |
|||
|
|
Chocolate |
Vanilla |
Strawberry |
Peanut |
|
Donalda’s mother |
No |
No |
Yes |
No |
|
Donalda’s father |
No |
No |
Yes |
No |
|
Donalda’s brother |
No |
No |
No |
Yes |
|
Donalda’s sister |
No |
No |
Yes |
No |
38. Donalda collected the information in the table as part of her research on the most popular flavor of ice cream. After interviewing several subjects and recording her data into the table, she came up with the following conclusions. Which is the most believable?
(A) Nobody likes chocolate ice cream.
(B) Nobody likes vanilla ice cream.
(C) Strawberry ice cream is the most popular flavor in the world.
(D) No conclusion is possible from this data.
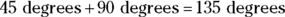to the right. If reading about this problem is confusing, draw it. Diagrams often make problems easier to visualize.
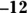. You can solve this equation by substituting 6 for y and 2 for z, which produces this equation: 
.
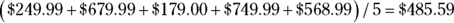. To determine the median price, you put all the prices in order; the middle one is the median. In this case, the median is $568.99 because it’s in the middle of the prices: $749.99, $679.99, $568.99, $249.99, and $179.00. The machine that comes closest to satisfying both criteria is the Super Suction 101 because its price is the same as the median. The difference between the price of the Super Suction 101 and the mean price is 
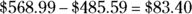. The difference between the price of the Hopper Model A1 and the mean price is 
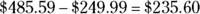, leaving the Super Suction 101 the clear mathematical winner.
One thing to keep in mind is that the mathematical problems on this test aren’t always reflections of reality. The technique used for buying vacuum cleaners in this question isn’t a reasonable way of buying anything, but it’s a good question because it tests your knowledge of the mean, median, and subtraction.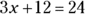
, you can subtract 12 from both sides so that 
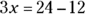, or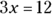 
; then divide both sides by 3 to find x, or 
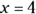. Again, remember the cardinal rule of equations: Whatever you do to one side, you must do to the other.
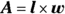. In each case, Rachel and Ronda have to calculate the area of the space they’re dealing with to get a price for the carpet and the paint. The formula for area is 
.
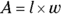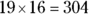square feet, the area of the bedroom is 
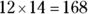square feet, and the area of the hallway is 
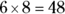square feet. The total area is the sum of the room areas or 
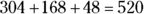square feet.
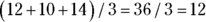blocks. To beat her average, she has to walk 13 blocks on Thursday. If she walks 12 blocks, she will equal (not beat) her average trip. All the other answers are less than her average.
.
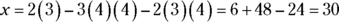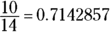, or 0.71 to 2 decimal places.
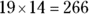square feet. The area of Bedroom B is 
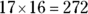square feet. Bedroom B is larger by 
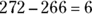square feet.
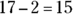feet, and the width would be 
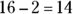feet. The reason you have to subtract 2 from each measurement is that the rug would be 1 foot from each wall, resulting in a rug that was 2 feet shorter than the room in each dimension. 
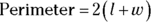, where l is the length and w is the width, so the perimeter of the 
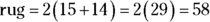feet.
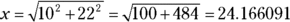, because you want the ladder to be long enough to reach the wall, the length has to be rounded up to 25 feet.
Pythagoras, a Greek mathematician, proved that the square of the hypotenuse of a right-angled triangle is equal to the sum of the squares of the other two sides. The hypotenuse is the side opposite the right angle. You find the Pythagorean theorem on the formula sheet you get with your test, so don’t forget to check it for important information you may need as you work through the questions.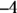
, it’s located on a line 4 units to the left of the y-axis.
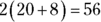. Choice (C) is the correct answer with the first two digits reversed (in other words, it’s a reminder to check your answers carefully!). Reversing digits under the stress of time limits isn’t impossible or unusual.
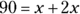or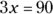 
, in which case 
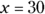. So Roger spent $30.00 for clothing.
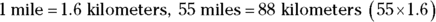. The speeds are both in units per hour, so 
.
.
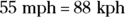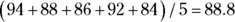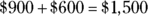for rent and living expenses. He has 
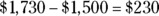left over.