Kapitel 4

Warum die Erde nicht flach ist (und wie man das beweisen kann)

Wie groß ist die Erde? Und welche Form hat sie eigentlich? Heute hat jeder Mensch eine gute Vorstellung davon, dass wir auf einer Kugel leben. Na ja, fast jeder Mensch. Es gibt ja tatsächlich eine nicht unbeträchtliche Anzahl von Leuten, die sich der Flat Earth -Bewegung angeschlossen und es sich zur Aufgabe gemacht haben, zu beweisen, dass die Erde flach ist. Wenig überraschend hatten sie damit bisher keinen Erfolg. Denn so funktioniert Wissenschaft zum Glück nicht. Man kann sich nicht das Ergebnis aussuchen und dann Experimente durchführen, um dieses Wunschziel zu erreichen. Wissenschaft ist der beste Prozess zur Wahrheitsfindung, den wir haben. Das Zauberwort hier heißt »Falsifikation«. Im Grunde versucht man in der Wissenschaft nicht, seine Theorie zu verifizieren, also zu belegen, sondern sie zu falsifizieren, also Beweise gegen die eigenen Annahmen zu finden. Je intensiver man versucht, eine Theorie zu widerlegen, und je öfter man dabei scheitert, desto plausibler wird die Theorie. Wenn man Unstimmigkeiten findet, kann man sich noch eine Weile mit Subhypothesen aushelfen (wir erinnern uns an die Epizykel des Ptolemäus), aber irgendwann wird jede nicht zutreffende Theorie unter einem Hagel an Falsifikationen zu Boden gehen. Der Korrektheit halber nennen wir große Ideen wie die Relativitätstheorie von Einstein oder die Evolutionstheorie von Darwin auch dann noch Theorien, wenn sie schon Hunderten oder sogar Tausenden von Falsifikationsversuchen standgehalten haben und allgemein als belegt gelten. Es könnte ja trotzdem sein, dass eines Tages eine neue Information aufkommt, die uns zwingt, noch einmal zu überdenken, was wir bislang als Wahrheit akzeptiert haben. Das ist genau die Unvoreingenommenheit, die die Wissenschaft zum besten Instrument macht, um herauszufinden, was nun wirklich stimmt, was wirklich ist.

Und die Form unserer Erde? Ist es auch nur eine Theorie, dass sie rund ist? Nicht wirklich. Spätestens seit dem 7 . Dezember 1972 wissen wir das ganz sicher. An diesem Tag nahmen die Astronauten der Apollo-17 -Mission auf ihrem Weg zum Mond das legendäre Foto Blue Marble auf. Es zeigt unseren Blauen Planeten aus einer Entfernung von 29000 Kilometern als das, was er wirklich ist: eine blaue Murmel, die im Schwarz des unendlichen Universums das Sonnenlicht reflektiert.

Es ist nicht mal das erste Farbfoto, das aus dem Weltall aufgenommen wurde (schon seit den 60 er-Jahren machten Satelliten Aufnahmen von unserem Planeten), aber Blue Marble ist nun mal das berühmteste Foto. Dennoch gibt es Leute, denen das nicht Beweis genug ist. Woher will man denn wissen, dass es sich nicht um ein Fake handelt? Gut. Ich war selbst nicht bei der Apollo-Mission dabei, aber es existieren noch andere Ansätze, wie man die Form unserer Erde überprüfen kann.

Schon früh beschäftigten sich Gelehrte mit dieser Frage. Einer der ersten Menschen, die auf die Idee kamen, dass wir auf einer Art Kugel leben, war der Mathematiker Pythagoras von Samos, der 500 Jahre v.u.Z. lebte. Wir kennen ihn wegen seiner legendären Erkenntnis, dass sich die Länge der Hypotenuse c eines rechtwinkligen Dreiecks aus der Wurzel der beiden Kathetenquadrate a und b berechnen lässt. Okay, das war unnötig kompliziert ausgedrückt. Einfacher gesagt:

a² + b² = c²

Den »Satz des Pythagoras« lernt jede Schülerin und jeder Schüler in der 8 . Klasse kennen. Dass Pythagoras diese Formel aber gar nicht erfunden hat, wissen die wenigsten. Schon im antiken Babylon, also über 1200 Jahre vor seiner Geburt, war das Verfahren bekannt. 86 Was noch weniger Menschen wissen, ist, dass Pythagoras von Samos nicht nur als Naturwissenschaftler in die Geschichtsbücher eingegangen ist, sondern auch als Zahlenfanatiker und Sektenanführer. Als er etwa 525 v.u.Z. nach Italien zog, gründete er die Bruderschaft der Pythagoreer, die nach dem Credo lebte: »Alles ist Zahl.« 87 Ihrer Überzeugung nach waren Zahlen heilig. Ganze Zahlen beteten sie geradezu an. Sie glaubten zudem an die Wiedergeburt, an einen universellen Geist, der allen Lebewesen innewohnt, und eben daran, dass ganze Zahlen das Universum regieren. Der Legende nach führte das auch zu einem der größten Skandale um die Bruderschaft. Als einer ihrer Anhänger, ein Mann namens Hippasos von Metapont, versuchte, die Wurzel aus zwei zu ziehen (er tat dies, um den Satz des Pythagoras anzuwenden auf ein Dreieck, dessen bekannte Seiten jeweils die Länge eins hatten), stieß er darauf, dass es so etwas wie irrationale Zahlen gibt. Irrationale Zahlen zeichnen sich dadurch aus, dass man sie nicht als Bruch von zwei ganzen Zahlen darstellen kann. Mit anderen Worten: Anscheinend lässt sich doch nicht alles im Universum mit ganzen Zahlen erklären. Ups. Diese Erkenntnis bedrohte die Kernüberzeugung der Pythagoreer, die Hippasos deshalb angeblich zur Strafe im Meer ertränkt und fortan versucht haben sollen, das Wissen um die irrationalen Zahlen geheim zu halten. 88 Eine durchaus verständliche Reaktion – das hätte ich auch gerne mit meinem Mathelehrer gemacht, als er damals mit irrationalen Zahlen um die Ecke kam.

Lange galt diese Geschichte als größter Skandal der Bruderschaft, neuere Forschung legt jetzt aber nahe, dass es sich womöglich doch nur um einen Übersetzungsfehler handelt. 89 Wie sich das alles genau zugetragen hat, lässt sich nicht mehr feststellen, klar ist aber, dass das Leben der Anhängerinnen und Anhänger des Pythagoras von Samos doch spannender war, als es rechtwinklige Dreiecke vermuten lassen.

Die Pythagoreer beschäftigten sich aber nicht nur mit Mathematik, sondern entwickelten auch ihre ganz eigene Kosmologie: Sie gingen davon aus, dass die Erde kugelförmig ist und das Zentrum des Universums bildet. 90 Diese Überzeugung beruhte zwar eher auf einem ästhetischen Verlangen nach Vollkommenheit als auf Experimenten und empirischen Daten, trotzdem waren sie damit der Wahrheit, mehr oder weniger aus Versehen, auf der Spur.

Rund 200 Jahre später griff der griechische Gelehrte Aristoteles diesen Gedanken auf, und zwar aus guten Gründen. Er hatte nämlich Folgendes beobachtet: Wenn ein Schiff am Horizont verschwindet, so ist erst der Rumpf nicht mehr zu sehen, danach die Segel. Zudem erkannte er, dass es der Schatten der Erde ist, der den Mond bei einer Mondfinsternis verdeckt; die runde Form dieses Schattens sprach ebenfalls für eine kugelförmige Gestalt der Erde. Zu guter Letzt führte Aristoteles ins Feld, dass man an unterschiedlichen Orten auf der Erde unterschiedliche Sternenkonstellationen sehen kann. 91 Und nur wenn wir auf einer Kugel leben, können wir im Norden andere Sterne sehen als im Süden, denn wir blicken buchstäblich in einen anderen Teil des Universums. Die Annahme, dass wir auf einer runden Erde leben, war damals also keine unbedeutende Theorie, die nur von einer Minderheit vertreten wurde, sondern galt als Fakt und wurde von den größten Lehrern der Antike vermittelt.

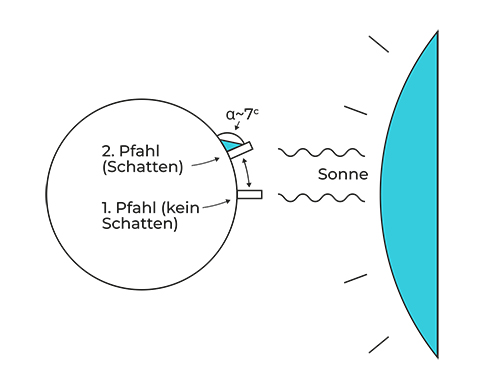
Aber es blieb nicht bei einfachen Beobachtungen und religiösem Fanatismus. Form und Größe unserer Erde wurden 300 Jahre v.u.Z. auch schon mithilfe eines einfachen Experiments erforscht, welches jeder und jede von uns mit zwei Holzpfählen und einem funktionierenden Gehirn selbst nachstellen kann. Der damalige Leiter der Bibliothek von Alexandria, ein Gelehrter namens Eratosthenes, wollte den Umfang von Aristoteles’ kugelförmiger Erde berechnen. Er erfuhr von einem Brunnen in Syene (im heutigen Ägypten), in den die Sonne jedes Jahr genau am 21 . Juni zur Mittagszeit so hineinschien, dass es an seinem Boden keinen Schatten gab. Dort stand die Sonne also zur Sommersonnenwende in einem perfekten rechten Winkel zur Erde. Eratosthenes verstand, dass es ihm mit diesem Wissen möglich sein würde, den Umfang der Erde zu berechnen. Wie das gehen sollte? Nun, stellen wir uns einen Kreis vor, auf dem wir an zwei Punkten jeweils einen Pfahl aufgestellt haben. Dazu kommt nun eine Lichtquelle, die aus einiger Entfernung diesen Kreis anleuchtet. Dort, wo die Lichtstrahlen im rechten Winkel auf den Kreis treffen, steht der erste Pfahl. In Eratosthenes’ Fall war das der Brunnen in Syene, darauf kommt es aber letztlich nicht an. Wichtig ist nur: Der Pfahl (respektive Brunnenrand) wirft keinen Schatten. Etwas weiter oben steht der zweite Pfahl. Dieser sollte, wenn die Erde wirklich eine Kugel ist, einen kleinen Schatten werfen. Wenn wir jetzt die Entfernung zwischen den beiden Pfählen und die Länge des Schattens, den der zweite Pfahl wirft, kennen, können wir ausrechnen, wie lang ein Grad dieses Kreises ist. Und da ein Kreis 360 Grad hat, müssen wir nur noch diese Strecke mal 360 nehmen, und schon haben wir den Kreisumfang berechnet.

Das Wissen über die wesentlichen Eigenschaften von Kreisen war im antiken Griechenland spätestens seit der Entwicklung der euklidischen Geometrie weit verbreitet. Euklid von Alexandria war Mathematiker und lebte im dritten Jahrhundert v.u.Z. In seinem monumentalen Werk Die Elemente stellte er wichtige geometrische Grundgesetze auf, die uns bei ebensolchen Berechnungen helfen. Was sind Winkel? Was ist eine Gerade? Was ist ein Punkt etc. 92

Bewaffnet mit der euklidischen Geometrie, machte sich unser Bibliotheksleiter Eratosthenes daran, das Rätsel um Form und Größe der Erde zu lösen. Er stellte in Alexandria einen Holzpfahl auf und maß die Länge des Schattens, den dieser an genau dem Tag zu genau der Uhrzeit verursachte, zu der in dem Brunnen in Syene kein Schatten zu sehen war. 4 Aus der Länge des Schattens in Alexandria berechnete Eratosthenes den Winkel, in dem dieser geworfen wurde. Er betrug 7 ,2 Grad, also genau 1 /50 eines kompletten Kreises. Wenn er jetzt noch die exakte Entfernung zwischen seinem Pfahl und dem Brunnen im weit entfernten Syene herausfinden konnte, hätte er alles, was er für seine Berechnungen brauchte. Zu diesem Zweck beauftragte Eratosthenes sogenannte Bematisten, die darin trainiert waren, immer gleich große Schritte zu laufen und auf diese Art große Entfernungen zu messen. Sie kamen auf eine Strecke von 5000 Stadien 5 zwischen Alexandria und Syene, was 800 bis 900 Kilometern entspricht. 93 Mithilfe dieser Werte berechnete Eratosthenes den Umfang der Erde auf etwa 40250 Kilometer, was nur ein Prozent über dem tatsächlichen Wert von 40072 Kilometern liegt! 94 Eratosthenes stellte diese Berechnung mit fast fehlerfreier Präzision knapp 250 Jahre v.u.Z. an, doch die meisten seiner Zeitgenossen zogen einen niedrigeren Wert vor: etwa 28000 km. 95 Diese falsche Zahl stand auch in Ptolemäus’ Almagest und wurde später von Kolumbus für seine Weltumseglung genutzt. Was war in der Zwischenzeit mit dem Wissen der antiken Griechen passiert? Wer war schuld, dass die nächsten Erkenntnisschritte so lange auf sich warten ließen? Es war der Aufstieg des Römischen Reiches, durch den das so hoch entwickelte Europa der cleveren Griechen zurückgeworfen wurde und der den Kontinent in die größte intellektuelle Krise aller Zeiten stürzte.