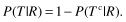
Answers to Selected Exercises

Exercise 2.11: One should always test R functions one has written by trying several combinations of inputs. Will your function work correctly if m > n? m < 0? Be sure to include solution messages such as

>  print("m must be less than or equal to n"); break

Exercise 2.13: 

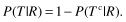
Exercise 3.7: 

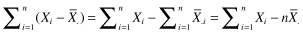
Exercise 3.14: 

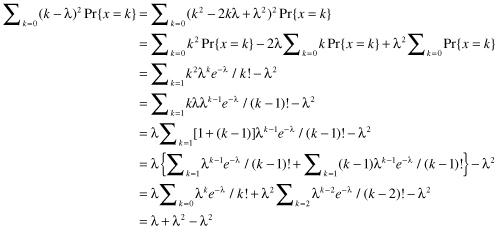
Exercise 4.7: 

sales=c(754,708,652,783,682,778,665,799,693,825,828,674,792,723)
t.test(sales, conf.level=0.9)

Exercise 5.4: The results will have a binomial distribution with 20 trials; p will equal 0.6 under the primary hypothesis, while under the alternative p will equal 0.45.

Exercise 5.5: You may want to reread Chapter 2 if you had trouble with this exercise.

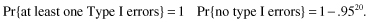
Exercise 8.2: 

> imp=c(2, 4, 0.5, 1, 5.7, 7, 1.5, 2.2)
> log(imp)
[1]  0.6931472  1.3862944 -0.6931472  0.0000000  1.7404662  1.9459101  0.4054651
[8]  0.7884574
> t.test(log(imp))
      One Sample t-test
data: log(imp)
t = 2.4825, df = 7, p-value = 0.04206
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval: 0.03718173 1.52946655 
sample estimates: mean of x 0.7833241 
#Express this mean as an after/before ratio
> exp(0.7833241)
[1] 2.188736

Exercise 8.11: 

#Define  F1
> Snoopy = c(2.5, 7.3, 1.1, 2.7, 5.5, 4.3) 
> Quick = c(2.5, 1.8, 3.6, 4.2 , 1.2 ,0.7)
> Mrs. Good's = c(3.3, 1.5, 0.4, 2.8, 2.2 ,1.0)
> size = c(length(Snoopy), length(Quick), length(MrsGood))
> data = c(Snoopy, Quick, MrsGood)
> f1=F1(size,data)
> N = 1600
> cnt = 0
> for (i in 1:N){
+     pdata = sample (data)
+     f1p=F1(size,pdata)
+     # counting number of rearrangements for which F1 greater than or equal to original
+   if (f1 <= f1p) cnt=cnt+1
+   }
>  cnt/N
[1] 0.108125

Exercise 9.17: This example illustrates the necessity of establishing a causal relationship between the predictor and the variable to be predicted before attempting to model the relationship.