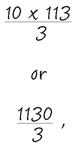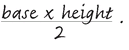MATH
Remember when you used to harangue your parents about why you needed to know “this stuff”? It was only later that you found out why as you wrestled with the challenges of chemistry, engineering, physics, architecture or more ordinary kinds of problems such as figuring your income tax and balancing your checkbook. That math you found so useless as a child is not so useless after all, is it? But perhaps over the years you have found yourself floundering for some of those rules and answers you might have known if you hadn’t been doodling on your notebook during class. Well, flounder no more.…
Arithmetic
Arithmetic is all about sums—adding, subtracting, multiplying, and dividing—each with its own vocabulary:
• If you add two or more numbers together, their total is a sum. So 7 is the sum of 4 + 3.
• With subtraction you find the difference between two numbers. The difference between 9 and 7 is the smaller number subtracted from the larger: 9 - 7, and the difference is 2.
• If you multiply two or more numbers together, the answer is a product. So 30 is the product of 6 x 5.
• With division you divide a divisor into a dividend and the answer is a quotient. If there is anything left over, it is called a remainder. So 15 divided by 2 gives a quotient of 7 with a remainder of 1.
• LONG MULTIPLICATION
If you are old enough to have taken math exams without the aid of a calculator, you will have learned the times tables. The easiest one is the 11 times table because it goes 11, 22, 33, 44, and so on—but it all goes a bit wrong after 99. Many people learn by rote up to 12 x 12 = 144; beyond that a person really needs to understand what they are doing. For example:
After the number 9, you have to use two digits. The right-hand digit in any whole number represents the units; to the left are the tens and then the hundreds and so on. So 63 is made up of 6 tens, or 60, plus 3 units. And in this problem, you need to multiply 147 by each of those elements separately.
Start from the right: 3 x 7 = 21, so you write down the 1 and “carry” the 2 to the next column;
3 x 4 = 12, plus the 2 you have carried = 14. Write down the 4 and carry the 1;
3 x 1 = 3, plus the 1 you carried = 4.
So 3 x 147 = 441.
To multiply 147 by 60, put a 0 in the right-hand column and multiply by 6 (because any number multiplied by 10 or a multiple of 10 ends in 0);
6 x 7 = 42, so write down the 2 and carry 4;
6 x 4 = 24, plus the 4 you have carried = 28. Write down the 8 and carry 2;
6 x 1 = 6, plus the 2 you have carried = 8.
So 60 x 147 = 8,820;
63 x 147 is therefore the sum of 60 x 147 (8,820) and 3 x 147 (441), which equals 9,261.
Or
Songwriter and mathematician Tom Lehrer plays a tune about New Math, in which he does his problem in base 8. If you do a search on
Youtube.com for Lehrer’s New Math, you’ll see why this section avoids that technique.
• LONG DIVISION
Division is multiplication in reverse, so start with 9,261 and divide it by 63.
If you have a divisor of 12 or less, the times tables does or did the work for you: You
know or knew that 72 divided by 8 was 9, without having to work it out. But with a number larger than 12, you need to be more scientific:
With division you work through the number from left to right.
You can’t divide 63 into 9, for the simple reason that 63 is larger than 9. So look at the next column. You can divide 63 into 92—once—so you write a 1 at the top of the sum. But it doesn’t go into 92 once exactly—there is a remainder, which is the difference between 92 and 63; in other words, 92 minus 63, which is 29.
Carry 29 forward into the next column and put it in front of the 6 to give you 296. Does 63 go into 296? Yes, it must, because 296 is bigger than 63, but how many times? Well, look at the left-hand figures of the two numbers and you’ll see something that you can solve using the times table: 6 into 29. That’s easy: Four 6s are 24, so 6 goes into 29 four times, with a bit left over. So it’s likely that 63 will go into 296 four times with a bit left over. Indeed 4 x 63 = 252, and the bit left over is 296 minus 252, which equals 44.
Write 4 at the top of the sum, next to the 1, and carry 44 forward into the next column to make 441. How many times does 63 go into 441? Well, 6 goes into 44 seven times (6 x 7 = 42), so let’s try that. And, conveniently, 63 x 7 = 441. Which means that 63 goes into 441 exactly seven times, with nothing left over, and that answers the problem: 147.
Fractions, Decimals, and Percentages
• PROPER FRACTIONS
A fraction is technically any form of number that is not a whole number; what most people think of as fractions—numbers such as ½, ⅔, ¾, and so on—are properly called vulgar, simple, or common fractions (as opposed to decimal fractions; see page 60).
The top number in these fractions is called the numerator, the bottom one the denominator (remember, denominator down).
In fact, the examples given above are all
proper fractions, with the numerator smaller than the denominator (the fraction represents less than 1). In an
improper fraction the reverse is true, as in
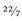
(an approximation for pi, see page 73), which can also be written as
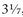
, because 7 goes into 22 three times, with a remainder of 1.
If you want to solve problems that involve fractions, it is important to know that if you divide or multiply both the numerator and denominator by the same number, you produce a fraction that is the same value as the original fraction. Take ½. Multiply both numerator and denominator by 2 and you get
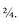
Which is still a half, because 2 is half of 4. Or multiply ½ by 3 and you get
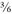
. Which again is still a half, because 3 is half of 6.
The same principle applies to division: If you start with
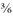
and divide top and bottom by 3, you reduce your fraction down to ½ again. This process is called canceling. When you can’t cancel anymore, the fraction is in its lowest terms.
With addition and subtraction, however, you can only add and subtract fractions that have the same denominator. You can add ½ + ½ and get
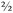
, which equals 1, because two halves make a whole. But what you have done is add the two numerators together. The denominator stays the same, because you are adding like to like. (It’s no different from adding 1 apple to 1 apple to get 2 apples.)
Now say you want to add ½ + ⅓. It’s easy to do, but first you must convert them so they have the same denominator. The lowest common denominator of 2 and 3 (the smallest number into which both will divide) is 6. To turn ½ into sixths, you need to multiply both parts of the fraction by 3:
So ½ is the same thing as
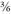
.
To convert ⅓ into sixths, you need to multiply both parts by 2:
So ⅓ is the same thing as
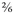
.
Now you have something that you can add, on the same principle of adding the numerators together:
The same applies to subtraction:
But both 4 and 10 can be divided by 2, to give the simpler fraction ⅖.
• DECIMAL FRACTIONS
The word decimal refers to anything with the number 10, and the English system is based on multiples of 10. As previously mentioned in the multiplication section, a single-digit number—say, 6—means that you have six units of whatever it is. When you have more than nine, you have to use two digits, with one digit representing the tens on the left and one digit representing the units on the right.
Decimal fractions work on the same principle, except that they go from right to left. The fraction is separated from the whole number by a dot called a
decimal point. The figure immediately to the right of it represents tenths, to the right of that is hundredths, and so on. So 1.1 (pronounced one point one) = 1 plus one tenth of 1; 1.2 = 1 + 2/10 (or ⅕); 1.25 (pronounced one point two five)
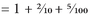
, or

.
An interesting example is 1.25, because it is the same as 1¼. How do we know that? Well, return to the idea of dividing numerators and denominators by the same thing. For example,
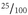
can be divided by 5 to give
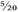
. But 5 and 20 are both also divisible by 5, giving ¼. (Once you’ve got your numerator down to 1, you know that you have simplified the fraction as far as it will go.) So 1.25 is exactly the same as 1¼.
Decimal fractions that are less than 1 can be written either 0.25 or just .25—it’s the same thing.
• RECURRING DECIMALS
Not everything divides neatly into tens, so sometimes a decimal fraction can be no more than an approximation. For example, ⅓ is 0.333 recurring—no matter how many threes you add, you will never get a decimal that is exactly equal to one third.
If a decimal recurs, you can be certain that it’s the same as some common fraction. For example, 0.222 recurring is
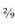
; 0.142857142857142857 recurring is
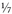
. A recurring decimal is sometimes indicated with a dot above the last digit, which is sort of the equivalent of ellipses (…) or “etc., etc., etc.”
Pi is different (see page 73). Its decimal expansion goes on forever but without recurring, because it isn’t the same as any common fraction. Pi is called a transcendental number, and it’s probably the only one you’ll ever meet.
• PERCENTAGES
Percent means
by a hundred, so anything expressed as a percentage is a fraction (or part, if you prefer) of 100. So 25 percent is twenty-five parts of 100, or
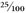
or 0.25. If you’ve been paying attention, you’ll know that this is the same as ¼.
Similarly, 50 percent is
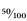
, which can be canceled down to
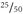
, which is
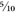
, which is ½.
Mean, Median, and Mode
In arithmetical terms,
mean is simply a fancy word for
average. You calculate a mean by adding a group of numbers together and dividing by the number of numbers. (Strictly speaking, this is the
arithmetic mean—there are other sorts of mean, too, but of interest only to mathematicians.) So the mean of 4, 8, 12, and 16 is the total of the four numbers, divided by 4:
4 + 8 + 12 + 16 = 40 divided by 4 = 10.
And it works for any number of numbers. For example, if a class of 11 children gets the following marks on an exam—55, 57, 57, 65, 66, 69, 70, 72, 75, 79, and 83—the total of the marks is 748. Divide that by 11, and you get a mean of 68.
The median of a set of values is literally the middle one. In the set of grades above, it is 69. There are five marks lower than 69 and five marks higher than 69—never mind their actual values. The median of an even number of values is the average of the middle two. For example, the median of 1, 4, 9, 16, 25, and 36 is 12.5—halfway between 9 and 16.
The mode of a set of values is the most common value. The mode of our set of marks is 57, because it is the only one that occurs more than once.
Measurements
Metric units and imperial (or what we will refer to as American) units are two different ways to measure the same things. Just as Fahrenheit and Celsius both measure temperature but in different ways (see page 94), so the metric system and system of American units quantify length, weight, and all sorts of other things, using different units. Metric units are also sometimes called SI units, which stands for Système Internationale.
The metric system calculates in tens or multiples of tens. The system of American units doesn’t, and to the uninitiated it can seem pretty random. (American units used to mean something sensible, such as the foot was the length of a man’s foot and the yard was the distance from his nose to the tip of his outstretched arm.)
• LENGTH
In American units length is measured in inches, feet, yards, and miles, and occasionally also in chains and furlongs. There are 12 inches in a foot, 3 feet (36 inches) in a yard, 22 yards in a chain, 10 chains in a furlong, and 8 furlongs (1,760 yards, 5,280 feet) in a mile. Other units are still in use for some special purposes, such as the fathom (6 feet) for measuring the depth of the sea, and the hand (4 inches) for measuring the height of a horse.
The basic unit of length in the metric system is the meter, with subdivisions and multiples for measuring little things and big things. Most commonly used are the millimeter (a thousandth of a meter), the centimeter (a hundredth of a meter, or ten millimeters), and the kilometer (a thousand meters).
To convert between the two:
• 1 inch = 2.54 centimeters, so to convert inches to centimeters, multiply by 2.54. To convert centimeters to inches, divide by 2.54. Remember that a centimeter is shorter than an inch, so you should have a larger number of centimeters.
• 1 yard = 0.91 meters; 1 meter = 1.09 yards, or 3.3 feet. Yards and feet are shorter than meters, so you will have a larger number of them.
• 1 mile = 1.6 kilometers; 1 kilometer = 0.625 (⅝) of a mile. This time the metric unit is smaller, so you have more kilometers than miles.
• A nautical mile is about 1.15 miles, or exactly 1,852 meters.
• WEIGHT
In American units weight is measured in ounces, pounds, a hundredweight (short), and tons: 16 ounces (oz.) = 1 pound (lb., from libra, Latin for pound); 100 pounds = 1 hundredweight (short); 200 hundredweight (2,000 lb.) = 1 ton. This is sometimes called a short ton, because the imperial system in the U.K. uses a long ton of 2,240 lb. And they also use a measurement of stones (14 pounds = 1 stone).
In the metric system weight is measured in grams or kilograms. (You can have milligrams and centigrams, but a gram is already pretty small, so unless you’re a pharmacist or something of that sort, you don’t often need them.) A kilogram is 1,000 grams.
• 1 gram (or g) = about 0.0353 ounce, so to convert grams to ounces, multiply the number of grams by .0353. To convert ounces to grams, divide by .0353.
• 1 kilogram (or kilo or kg) is about 2.2 pounds, so multiply kilograms by 2.2, divide pounds by 2.2.
• A metric ton is 1,000 kilograms, or 2,205 pounds, just a bit more than an American ton.
• VOLUME
In the American system volume is measured in fluid ounces, pints, quarts, and gallons; in the metric system it is measured in liters. This becomes even more complicated because the value of the units in the United States differs from the imperial system in the U.K.
In the United States 16 fluid ounces make a pint. But the U.S. pint and gallon are smaller than the U.K. ones. To convert U.S. pints to liters, divide by 2.1.
In the U.K. 20 imperial fluid ounces make 1 imperial pint, 2 imperial pints make 1 imperial quart, and there are 4 quarts (8 pints) in an imperial gallon. A liter is about 1.75 pints, so to convert imperial pints to liters, divide by 1.75; to convert liters to imperial pints, multiply by 1.75 (pints are smaller, so you will have more of them).
Algebra and Equations
Algebra is the branch of math that uses symbols (normally letters of the alphabet) to represent unknown numbers, along the lines of a + b = 5. If you assign a value to a, you can calculate b: If a = 2, then b = 3. This is known as an algebraic equation.
The main thing to remember when solving equations is that one side of the = sign is equal to the other side, so anything that you do to one side, you need to do to the other.
2For example, to solve the equation
you first add 2
a to each side, giving:
Then subtract 1 from each side, giving
Now you can divide both sides by 5 and announce proudly that a = 3.
• SIMULTANEOUS EQUATIONS
A simultaneous equation is a more complicated form of algebraic equation, in which you have two or more unknowns. The general rule is that you must have exactly the same number of equations as you have unknowns in order to find the value of each. If you have fewer equations, there will be lots of solutions and no way to choose between them. If you have too many equations, there will be no solution at all.
This assumes that the equations are all different and don’t contradict each other. For example:
are no good as a pair of simultaneous equations, because they both say exactly the same thing, while:
will not work either, because there’s no way both of them can be true at the same time.
Here’s a look at a better-behaved set of simultaneous equations:
A way of solving these is to add the two equations together, so
or, more simply, 2
a = 8 (because the +
b and -
b cancel each other out).
From there you can calculate that a = 4 and, because a + b = 6, b must equal 2. Which is verified by the second equation, 4 - 2 = 2.
The principle remains the same regardless of how many unknowns you have:
a + b + c = 24,
a + b - c = 16,
2a + b = 32.
Add the first two equations together and you get 2a + 2b = 40 (because this time the c’s cancel each other out).
Now look at the third equation. It’s very similar to the sum of the first two. Subtract one from the other:
(2a + 2b) - (2a - b) = 40 - 32.
The a’s cancel each other out, so 2b - b (in other words, b) = 8.
Go back to the third equation, which contains only
a’s and
b’s, and substitute 8 for
b:
Deduct 8 from each side of the equation to give
which means that
a = 12.
Now go back to the first equation and substitute both
a and
b:
12 + 8 + c = 24,
20 + c = 24,
c = 24 - 20 = 4.
Verify this by going to the second equation:
12[a] + 8[b] - 4[c] = 16,
which is true.
• QUADRATIC EQUATIONS
These are more complex again, because they involve a square—that is, a number multiplied by itself and written with a raised 2 after it—so 16 is 42, and 36 is 62. Thus, 4 is the square root of 16, and 6 is the square root of 36. The symbol for a square root is √. Actually, (-4)2 is also 16, so 16 has two square roots: +4 and -4. Any positive number has two square roots. A negative number doesn’t have any square roots at all, because if you multiply a negative by a negative, you get a positive.
An algebraic expression can also be a square: the square of
a + 4 is (
a + 4) x (
a + 4). You do this by multiplying each of the elements in the first bracket by each of the elements in the second:
(axa) + (ax4) + (4xa) + (4x4)
= a2 + 8a + 16.
To solve a quadratic equation, you need to turn both sides of it into a perfect square, which is easier to explain if we look at an example:
The rule for “completing the square” in order to solve a quadratic equation is, “Take the number before the
a, square it, and divide by 4.” For example, 8 squared (64) divided by 4 is 16, so we add that to both sides; reassuringly, we already know that adding 16 to this equation will create a perfect square, because we just did it in the previous equation:
a2 + 8a + 16 = 48 + 16 = 64 .
Taking the square root of each side gives:
a + 4 = 8 (because 8 is the square root of 64).
Again, we know that a + 4 is the square root of a2 + 8a + 16, because it was part of the sum we did on the previous page. Anyway, we now have a simple sum to establish that a = 4.
Wait a minute, though. Taking the square root of both sides of an equation is not allowed. Why is this? Because a positive number like 64 has
two square roots, +8 and -8. So the truth of the matter is that actually
so
a equals either +4 or -12.
Although this example is an easy one, the beauty of algebra is that the same principle applies whatever the numbers involved. So, to repeat: The rule for “completing the square” in order to solve a quadratic equation is, Take the number before the a, square it, and divide by 4.)
So if your equation is
you first simplify the equation by getting rid of the 14. Subtract it from both sides to leave:
Square the 12 to give 144, divide by 4 to give 36, and—as always—add that to both sides:
a2 + 12a + 36 = 19 + 36 = 55.
The square root of that gives you
a + 6 = 55 = (approximately) 7.4, or, of course, -7.4.
Deduct 6 from each side to leave the simple statement a = 1.4 or -13.4.
You can check that this is right by going back to the original equation and putting in
a = 1.4:
a2 + 12a + 14 = 33 becomes
(1.4 x 1.4) + (12 x 1.4) + 14 = 1.96 + 16.8 + 14
(near enough for the purposes of this exercise)
= 2 + 17 + 14 = 33.
QED, as they say in math (or essentially, problem solved). You’ll find it also works out with a = -13.4.
Geometry
Geometry is about measuring lines and angles and assessing the relationship between them, so let’s start with some ways of measuring.
• The perimeter of a two-dimensional object is the total length of all its sides. For example, if these sides are straight, it’s a matter of simple addition: A rectangle measuring 4 inches by 5 inches has two sides 4 inches long and two sides 5 inches long, so its perimeter is 4 + 5 + 4 + 5 = 18 inches.
• The area of a four-sided figure is calculated by multiplying the length by the width: In the above example 4 x 5 = 20 square inches (in.2).
• Volume is calculated in the same way, by multiplying the length by the width by the height (or, if you prefer, the area by the height). For instance, a box that is 6 inches high, whose base measures 4 inches by 5 inches, has a volume of 4 x 5 x 6 = 120 cubed inches (in3).
The volume of a pyramid is the area of the base multiplied by the height, divided by 3:
It’s when you get to circles that it all becomes more complicated, because then you have to start dealing with…
• PI
Pi (π) is the Greek equivalent of the Roman
p and is used in math to represent the ratio of the circumference of a circle to its diameter. Depending on how sophisticated you are as a mathematician, you can say that π = 3.142, 3.14159, or 3.1415926535897932384626433832795, but even then it is not 100 percent exact. Expressed as a fraction, pi is roughly 3
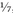
, or 22/7.
Before we go on, three more quick definitions:
• The circumference of a circle is its perimeter, the distance around the outside.
• The diameter is the length of a straight line through the middle, from one point on the circumference to another.
• The radius is half the diameter; that is, the distance from the center of the circle to the circumference.
So to calculate the circumference of a circle, you multiply the diameter by π: a circle that is, say, 7 inches in diameter has a circumference of 7 x 22/7 = approximately 22 inches. The formula for this can be expressed as πd, but is usually given as 2(πr).
Area is πr2—that is, π times the radius squared. So a circle of 6 inches radius has an area of 22/7 x (6 x 6) = approximately 113 square inches.
The three-dimensional equivalent to a circle is a sphere, and its volume is calculated by the formula 4/3πr3—that is, four thirds (or one and one third) of the product of π and the radius cubed (multiplied by itself and then by itself again). So a sphere with a radius of 6 inches has a volume of 4/3 x π x(6 x 6 x 6) = approximately 905 cubic inches.
A
cone is effectively a pyramid with a circular base, so the pyramid formula applies: A cone with a base 6 inches in diameter and a height of 10 inches has a base area of π x (6 x 6) = approximately 113 square inches, and a volume of:
which equals approximately 377 cubic inches.
• TRIANGLES
The area of a triangle is calculated by:
There are three types of triangles, depending on the length of their sides:
• An equilateral triangle has three sides of equal length.
• An isosceles triangle has two sides of equal length.
• A scalene triangle has three sides that are all of different lengths.
The sum total of the angles of a triangle, whatever its shape, is 180°. A right angle is 90°; any angle smaller than 90° is called an acute angle, while anything above 90° but lower than 180° is obtuse. In a right-angled triangle the side opposite the right angle (also always the longest side) is called the hypotenuse, which brings us neatly to…
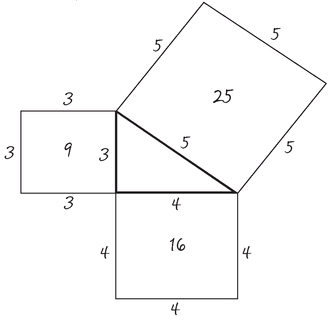
• THE PYTHAGOREAN THEOREM
This theorem states that the square on the hypotenuse is equal to the sum of the squares on the other two sides. The simplest example of this is what is called a 3:4:5 triangle, in which the hypotenuse is 5 inches (or centimeters or miles, it doesn’t matter) and the other two sides are 3 inches and 4 inches.
The square on the side that is 3 inches long is 9 in.2 (3 x 3), the square on the 4-inch side is 16 in.2 (4 x 4), and when you add them together, you get 25 in.2, which is the square of the hypotenuse (5 x 5).
This can also be remembered using the formula a2 + b2 = c2, where c is the hypotenuse.
The burning question, of course, is, Why does it matter? Well, it could have had some practical value in the ancient world. It has been suggested, for example, that the Egyptians could have used ropes in the proportion 3:4:5 to produce right angles when building the pyramids. Unfortunately, there isn’t the remotest scrap of evidence that they did any such thing. In fact, the Pythagorean theorem matters most to mathematicians because it is fundamental to our next topic.
Trigonometry
Trigonometry is “the branch of mathematics that deals with the relations between the sides and angles of a triangle,” and a trigonometric function is “any function of an angle that is defined by the relationship between the sides and angles of a right-angled triangle.”
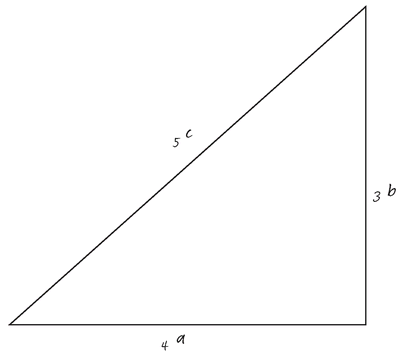
There are six basic trigonometric functions: sine, cosine, tangent, cotangent, secant, and cosecant, and they are calculated as follows. In a right-angled triangle where the other two angles are valued at
x and
y degrees, the side opposite
x is
a, the side opposite
y is
b, and the hypotenuse is
c:
sin x = a/c
cos x = b/c
tan x = a/b
cot x = b/a
sec x = c/b
cosec x = c/a
Why do we care? Well, the point is that the functions or ratios remain the same whatever the size of the triangle. So if you know the sine of a 90° angle in a triangle whose sides measure 3, 4, and 5 inches, you can extrapolate all sorts of measurements for a much larger triangle with the same proportions.
The trigonometric version of the Pythagorean theorem tells us that for any angle
x,
where sin
2x is a conventional way of writing (sin
x)
2 without the need for brackets. If you know the sine of an angle, you can use this formula to calculate all the rest of the trigonometric functions given above.
Trigonometry is vital to the study of higher mathematics and the sciences. At a more comprehensible and practical level, it is used in land surveying, mapmaking, engineering, astronomy, geography, satellite navigation systems, and so on.

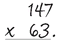
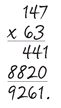

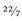 (an approximation for pi, see page 73), which can also be written as
(an approximation for pi, see page 73), which can also be written as 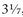 , because 7 goes into 22 three times, with a remainder of 1.
, because 7 goes into 22 three times, with a remainder of 1.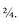 Which is still a half, because 2 is half of 4. Or multiply ½ by 3 and you get
Which is still a half, because 2 is half of 4. Or multiply ½ by 3 and you get 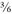 . Which again is still a half, because 3 is half of 6.
. Which again is still a half, because 3 is half of 6.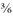 and divide top and bottom by 3, you reduce your fraction down to ½ again. This process is called canceling. When you can’t cancel anymore, the fraction is in its lowest terms.
and divide top and bottom by 3, you reduce your fraction down to ½ again. This process is called canceling. When you can’t cancel anymore, the fraction is in its lowest terms.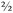 , which equals 1, because two halves make a whole. But what you have done is add the two numerators together. The denominator stays the same, because you are adding like to like. (It’s no different from adding 1 apple to 1 apple to get 2 apples.)
, which equals 1, because two halves make a whole. But what you have done is add the two numerators together. The denominator stays the same, because you are adding like to like. (It’s no different from adding 1 apple to 1 apple to get 2 apples.)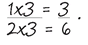
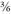 .
.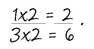
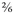 .
.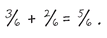
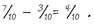
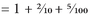 , or
, or  .
.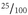 can be divided by 5 to give
can be divided by 5 to give 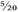 . But 5 and 20 are both also divisible by 5, giving ¼. (Once you’ve got your numerator down to 1, you know that you have simplified the fraction as far as it will go.) So 1.25 is exactly the same as 1¼.
. But 5 and 20 are both also divisible by 5, giving ¼. (Once you’ve got your numerator down to 1, you know that you have simplified the fraction as far as it will go.) So 1.25 is exactly the same as 1¼.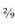 ; 0.142857142857142857 recurring is
; 0.142857142857142857 recurring is 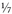 . A recurring decimal is sometimes indicated with a dot above the last digit, which is sort of the equivalent of ellipses (…) or “etc., etc., etc.”
. A recurring decimal is sometimes indicated with a dot above the last digit, which is sort of the equivalent of ellipses (…) or “etc., etc., etc.”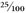 or 0.25. If you’ve been paying attention, you’ll know that this is the same as ¼.
or 0.25. If you’ve been paying attention, you’ll know that this is the same as ¼.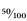 , which can be canceled down to
, which can be canceled down to 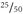 , which is
, which is 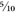 , which is ½.
, which is ½.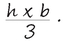
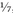 , or 22/7.
, or 22/7.