Chapter 17
Binary Mania
In This Chapter
Getting to know binary digits
Showing binary output
Working with bitwise operators
Setting and masking bits
Shifting bits
Understanding hexadecimal
Computers are digital devices, bathed in the binary waters of ones and zeros. Everything your programs deal with — all the text, graphics, music, video, and whatnot — melts down to the basic digital elements of one-zero, true-false, on-off, yes-no. When you understand binary, you can better understand computers and all digital technology.
Binary Basics
Happily, you don’t have to program any digital device by writing low-level code, flipping switches, or soldering wires. That’s because today’s programming happens at a higher level. But still, deep within the machine, that type of low-level coding continues. You’re just insulated from the primordial soup of ones and zeros from which all software rises.
Understanding binary
The binary digits, or bits, are 1 and 0. Alone, they’re feeble; but in groups, they muster great power. Digital storage uses these bits in groups, as illustrated in Table 17-1.
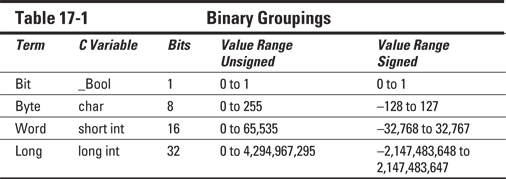
The advantage of grouping bits into bytes, words, and so on is that it makes them easier to handle. The processor can better deal with information in chunks. How chunks get their values is based upon powers of 2, as shown in Table 17-2.
Table 17-2 Powers of 2
|
Expression |
Decimal Value |
Binary Value |
|
20 |
1 |
1 |
|
21 |
2 |
10 |
|
22 |
4 |
100 |
|
23 |
8 |
1000 |
|
24 |
16 |
10000 |
|
25 |
32 |
100000 |
|
26 |
64 |
1000000 |
|
27 |
128 |
10000000 |
In Table 17-1, you see the range of values that can be stored in 8 bits, or 1 byte. It's the same range you'd find in a C language char variable. Indeed, if you total Column 2 in Table 17-2, you get 255, which is the number of bits in a byte.
Actually, you’ll find 256 possible values for a byte, which includes the all-zero permutation. That’s a value as well.
Figure 17-1 illustrates how the powers of 2 map into binary storage. Just as decimal places in a base 10 number increase by powers of 10, bits in a binary number increase by powers of 2, reading from right to left.
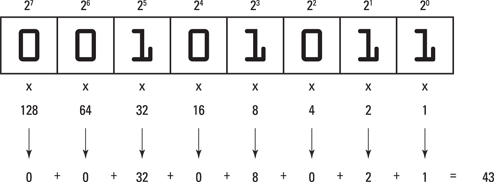
Figure 17-1: Base 2 values in a byte.
Each bit that's set, or has the value 1 in Figure 17-1, represents a power of two: 25, 23, 21, and 20. When you multiply these values by their decimal counterparts and then total them up, you get the decimal representation of binary 00101011, which is 43.
That’s all well and good, but please don’t memorize it!
Don’t concern yourself with translating binary into decimal values; the computer does that job for you all the time. Indeed, the computer sees only binary and then displays decimal numbers as a courtesy for your human eyeballs. But when you manipulate binary values, it helps to know what’s going on.
Changing a bit’s value to 1 is referred to as setting the bit.
Changing a bit’s value to 0 is referred to as resetting a bit.
Displaying binary values
To best make sense of the C language's binary manipulation operators, it helps to see a binary number in action. The printf() function lacks a binary conversion character, and the C library doesn't host a binary output function. Nope, to view a binary number, you have to craft your own function.
Listing 17-1 presents a binary output function I've concocted called binbin(). The binbin() function, at Line 15 in Listing 17-1, swallows an int value. Its output is a string representing that int value in binary digits.
Listing 17-1: The binbin() Function
#include <stdio.h>
char *binbin(int n);
int main()
{
int input;
printf("Type a value 0 to 255: ");
scanf("%d",&input);
printf("%d is binary %s\n",input,binbin(input));
return(0);
}
char *binbin(int n)
{
static char bin[9];
int x;
for(x=0;x<8;x++)
{
bin[x] = n & 0x80 ? '1' : '0';
n <<= 1;
}
bin[x] = '\0';
return(bin);
}
Generally speaking, at this point in the chapter, the contents of the binbin() function appear rather mysterious. That's okay. The details are offered in the later section Explaining the binbin() function, and the char * thing at the start of the function is discussed in Chapter 19.
Exercise 17-1: Type the source code from Listing 17-1 into a new project. Build and run it a few times to see how integers appear as binary numbers. Try the value 43 to confirm that I got it right in Figure 17-1.
As written in Listing 17-1, binbin() displays only 8 bits of data, though the int variable type typically stores many more bits.
Exercise 17-2: Modify the binbin() function from Listing 17-1 so that it displays 16 bits of the int value. (Well, technically, 16 bits is a short int.) To do so, you need to change these items:
Line 9: Alter the text so that 65535 is specified instead of 255.
Line 17: Modify the size of the array to 17 to account for 16 characters in the output plus the \0 (null character) at the end of the string.
Line 20: Adjust the immediate value 8 in the code to 16 to account for all 16 characters in the output.
Line 22: Replace the value 0x80 with 0x8000. This change makes the bit field larger, which is something you'll understand better after completing this chapter.
Build Exercise 17-2. Run it a few times to see what the bit field looks like for larger values.
The binbin() function, or a variation of it, is used in the following sections to help describe binary programming. You will copy and paste that function frequently, and feel free to use it in your own code however you deem appropriate.
Bit Manipulation
A smattering of C language operators provide data manipulation at the binary level. The operators are easy to ignore, but only when their true power and usefulness aren’t appreciated.
Using the bitwise | operator
You're already familiar with the decision-making logical operators: && for AND and || for OR. In the && evaluation, both items must be true for the statement to be evaluated as true; for the || evaluation, only one of the items must be true.
At the atomic level, the operators & and | perform similar operations, but on a bit-by-bit basis. The net effect is that you can use the & and | operators to manipulate individual bits:
The | is the bitwise OR operator, also known as the inclusive OR.
The & is the bitwise AND operator.
Listing 17-2 demonstrates how to use the bitwise OR operator to set bits in a byte. The OR value is defined as the constant SET at Line 2. It’s binary 00100000.
Listing 17-2: The OR Set
#include <stdio.h>
#define SET 32
char *binbin(int n);
int main()
{
int bor,result;
printf("Type a value from 0 to 255: ");
scanf("%d",&bor);
result = bor | SET;
printf("\t%s\t%d\n",binbin(bor),bor);
printf("|\t%s\t%d\n",binbin(SET),SET);
printf("=\t%s\t%d\n",binbin(result),result);
return(0);
}
char *binbin(int n)
{
static char bin[9];
int x;
for(x=0;x<8;x++)
{
bin[x] = n & 0x80 ? '1' : '0';
n <<= 1;
}
bin[x] = '\0';
return(bin);
}
Line 12 calculates the bitwise OR operation between a value input, bor, and the SET constant. The result is displayed in three columns: operator, binary string, and decimal value. The end result of the operation is that the bits set to 1 in the SET value will also be set to 1 in the bor value.
Exercise 17-3: Type the source code from Listing 17-2 into your editor to create a new program. Build and run the program.
Here's the output I see for the value 65:
Type a value from 0 to 255: 65
01000001 65
| 00100000 32
= 01100001 97
You can see in the binary output how the sixth bit is set in the result.
What does that mean?
It means that you can manipulate values at the binary level, which does have interesting consequences for certain mathematical operations, as shown in Listing 17-3.
Listing 17-3: Up with That Text
#include <stdio.h>
int main()
{
char input[64];
int ch;
int x = 0;
printf("Type in ALL CAPS: ");
fgets(input,63,stdin);
while(input[x] != '\n')
{
ch = input[x] | 32;
putchar(ch);
x++;
}
putchar('\n');
return(0);
}
Exercise 17-4: Start a new project by using the source code shown in Listing 17-3. Build and run.
Because of the way the ASCII codes map between upper- and lowercase characters, you can switch the case by simply setting the sixth bit in a byte.
Using bitwise &
Like the bitwise OR operator, the bitwise AND operator, &, also affects bits in a byte. Unlike OR, which sets bits, the AND operation masks bit values. It's easier to show you a program example than to fully describe what mask means.
Exercise 17-5: Modify the source code from Listing 17-2 so that a bitwise AND operation takes place instead of a bitwise OR. Change the constant SET in Line 2 to the value 223. Change the | (bitwise OR) in Line 12 to the & (bitwise AND). And finally, change the printf() statement in Line 15 so that the | is replaced by the & character. Build and run.
Here’s the output I see when I type the value 255 (all bits set):
Type a value from 0 to 255: 255
11111111 255
& 11011111 223
= 11011111 223
The bitwise & masks out the sixth bit, causing its value to be reset to 0 in the final calculation. No other bits are affected. To see more examples, try the values 170 and 85. Watch how the bits fall through the mask.
Exercise 17-6: Modify the source code from Listing 17-3 so that a bitwise AND operation takes place instead of a bitwise OR. Change Line 9 so that the printf() statement prompts: "Type in some text:" Change Line 14, replacing | with & and replacing the value 32 with 223. Build and run.
Just as the bitwise OR sets the sixth bit to convert uppercase text to lowercase, masking the sixth bit with a bitwise AND converts lowercase text into uppercase. Of course, the bitwise AND also masks out the space character, changing its value to 0, which isn’t a displayable character.
Exercise 17-7: Modify your solution for Exercise 17-6 so that only letters of the alphabet are affected.
Operating exclusively with XOR
XOR is the exclusive OR operator, yet another bitwise logical operator. And to answer your most pressing question, you pronounce XOR like “zor.” It’s the perfect evil name from bad science fiction.
The XOR operation is kind of weird, but it does have its charm. In the XOR operation, bits are compared with one another, just like the & and | operators. When two bits are identical, XOR coughs up a 0. When the two bits are different, XOR spits out a 1. As usual, a program example helps explain things.
The C language XOR operator is the caret character: ^. You can find it put into action on Line 14 in Listing 17-4.
Listing 17-4: It’s Exclusive or
#include <stdio.h>
char *binbin(int n);
int main()
{
int a,x,r;
a = 73;
x = 170;
printf(" %s %3d\n",binbin(a),a);
printf("^ %s %3d\n",binbin(x),x);
r = a ^ x;
printf("= %s %3d\n",binbin(r),r);
return(0);
}
char *binbin(int n)
{
static char bin[9];
int x;
for(x=0;x<8;x++)
{
bin[x] = n & 0x80 ? '1' : '0';
n <<= 1;
}
bin[x] = '\0';
return(bin);
}
Exercise 17-8: Type the source code from Listing 17-4 into your editor. Build and run to see how the XOR operation affects binary values.
The charming thing about the XOR operation is that if you use the same XOR value on a variable twice, you get back the variable’s original value.
Exercise 17-9: Modify the source code from Listing 17-4 so that one more XOR operation takes place. Insert these three statements after Line 15:
printf("^ %s %3d\n",binbin(x),x);
a = r ^ x;
printf("= %s %3d\n",binbin(a),a);
Build and run. The output looks like this:
01001001 73
^ 10101010 170
= 11100011 227
^ 10101010 170
= 01001001 73
Using the same XOR value of 170 turns the value 73 first into 227 and then back to 73.
Because XOR is the exclusive OR operator, some programmers refer to the standard bitwise OR operator as the inclusive OR operator.
Understanding the ~ and ! operators
Two infrequent binary operators are the ~ (or 1's complement) and the ! (or NOT). They lack the charm of the logical bitwise operators, but I suppose that they have a place.
The 1’s complement operator flips all the bits in a value, turning a 1 into a 0 and a 0 into a 1. For example:
~01010011 = 10101100
The ! (NOT) operator affects the entire value — all the bits. It changes any nonzero value to 0, and the value 0 to 1:
!01010011 = 00000000
!00000000 = 00000001
Zero and 1 are the only two results possible when using the bitwise ! operator.
Both the ~ and ! operators are unary operators — you simply prefix a value to get the results.
Table 17-3 lists a summary of C’s binary operators.
Shifting binary values
The C language features two binary operators that perform the equivalent operation of "Everyone move one step to the left (or right)." The << and >> operators shift bits in value, marching them to the left or right, respectively. Here's the format for the << operator:
v = int << count;
int is an integer value. count is the number of places to shift the value's bits to the left. The result of this operation is stored in variable v. Any bits that are shifted to the left beyond the width of the int variable x are lost. New bits shifted in from the right are always 0.
As with most binary nonsense, it helps to visually see what’s going on in a value when its bits are shifted. Therefore, I present Listing 17-5.
Listing 17-5: Everyone Out of the Pool!
#include <stdio.h>
char *binbin(int n);
int main()
{
int bshift,x;
printf("Type a value from 0 to 255: ");
scanf("%d",&bshift);
for(x=0;x<8;x++)
{
printf("%s\n",binbin(bshift));
bshift = bshift << 1;
}
return(0);
}
char *binbin(int n)
{
static char bin[9];
int x;
for(x=0;x<8;x++)
{
bin[x] = n & 0x80 ? '1' : '0';
n <<= 1;
}
bin[x] = '\0';
return(bin);
}
The shift operation takes place at Line 15 in Listing 17-5. The value in variable bshift is shifted to the left one bit.
Exercise 17-10: Type the source code from Listing 17-5 into your editor and build a new project.
The net effect of a left bit shift is to double a value. That holds true to a certain point: Obviously, the farther left you shift, some bits get lost and the value ceases to double. Also, this trick works only for unsigned values.
Exercise 17-11: Modify the source code from Listing 17-5 so that the printf() function at Line 14 also displays the decimal value of the bshift variable. You should also modify the binbin() function so that it displays 16 digits instead of 8. (Refer to Exercise 17-2 for the 16-bit binbin() solution.)
Here's the output I see when using the value 12:
Type a value from 0 to 255: 12
0000000000001100 12
0000000000011000 24
0000000000110000 48
0000000001100000 96
0000000011000000 192
0000000110000000 384
0000001100000000 768
0000011000000000 1536
Try the value 800,000,000 (don’t type the commas) to see how the doubling rule fails as the values keep shifting to the left. Also see the nearby sidebar Negative binary numbers.
The >> shift operator works similarly to the << shift operator, though values are marched to the right instead of the left. Any bit that's marched off the right end is discarded, and only zero bits are inserted on the left side. Here's the format:
v = int >> count;
int is an integer value, and count is the number of places to shift the bits to the right. The result is stored in variable v.
Exercise 17-12: Modify the source code from Exercise 17-11 so that the right shift operator is used instead of the left shift at Line 15. Build the program.
Here's the result I see when using the value 128:
Type a value from 0 to 255: 128
0000000010000000 128
0000000001000000 64
0000000000100000 32
0000000000010000 16
0000000000001000 8
0000000000000100 4
0000000000000010 2
0000000000000001 1
The << and >> operators are available only in the C language. In C++, similar operators are used to receive standard input and send standard output.
Explaining the binbin() function
If you've worked through this chapter from front to back, I can now sanely explain what's going on in the binbin() function to make it convert values into a binary string. Two statements do the job:
bin[x] = n & 0x80 ? '1' : '0';
n <<= 1;
The first statement performs an AND mask with the value n. All but the leftmost bit in the number is discarded. If that bit is set, which makes it a TRUE condition, the character 1 is stored in the array; otherwise, the character 0 is stored. (Refer to Chapter 8 to review the ternary operator, ?:.)
Negative binary numbers
Binary numbers are always positive, considering that the values of a bit can be only 1 or 0 and not –1 and 0. So how does the computer do signed integers? Easy: It cheats.
The leftmost bit in a signed binary value is known as the sign bit. When that bit is set (equal to 1), the value is negative for a signed int. Otherwise, the value is read as positive.
In this example, the sign bit is set for a signed char. The values expressed are negative, which is in the range of a signed char variable.
In this example, the sign bit is ignored because the value is an unsigned char. The values can only be positive, which is why the positive range for an unsigned variable is greater than for a signed variable.
The value is expressed as 0x80, which is hexadecimal notation, a type of shorthand for binary. (See the next section, The Joy of Hex.) The hex value 0x80 is equal to 10000000 binary, which is the AND mask. If the value is 16 bits instead of 8, 0x8000 is used instead, which creates a 16-bit binary mask.
The second statement shifts the bits in the value n one notch to the left. As the loop spins, working through the value n, another bit in the value is shifted to the leftmost position. That bit is evaluated, and the binary string is built by inserting a '1' or '0' character.
The Joy of Hex
Face it: No one wants to count bits in a binary number. No one. Perhaps some nerd somewhere can tell you that 10110001 is really the value 177 (I had to look it up), but most programmers can’t. What a good programmer can do, however, is translate binary into hex.
Hex has nothing to do with Harry Potter. It’s short for hexadecimal, which is the base 16 counting system. That’s not as obtuse as it sounds because it’s easy to translate between base 16 (hex) and binary.
For example, the value 10110001 translates into B1 hexadecimal. I can see that at once because I've been using hex for a while. It also means that I accept that hexadecimal numbers include the letters A through F, representing decimal values 10 through 15, respectively. A B in hex is the decimal value 11. Letters are used because they occupy only one character space.
Table 17-4 shows the 16 hexadecimal values 0 through F and how they relate to four bits of data.
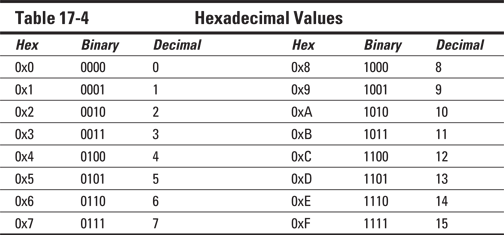
The hexadecimal values shown in Table 17-4 are prefixed with 0x. This prefix is common in C, although other programming languages may use different prefixes or a postfix.
The next hexadecimal value after 0xF is 0x10. Don’t read it as the number ten, but as “one zero hex.” It’s the value 16 in decimal (base 10). After that, hex keeps counting with 0x11, 0x12, and up through 0x1F and beyond.
Yes, and all of this is just as much fun as learning the ancient Egyptian counting symbols, so where will it get you?
When a programmer sees the binary value 10110100, he first splits it into two 4-bit nibbles: 1011 0100. Then he translates it into hex, 0xB4. The C programming language does the translation as well, as long as you use the %x or %X conversion characters, as shown in Listing 17-6.
Listing 17-6: A Little Hex
#include <stdio.h>
char *binbin(int n);
int main()
{
int b,x;
b = 21;
for(x=0;x<8;x++)
{
printf("%s 0x%04X %4d\n",binbin(b),b,b);
b<<=1;
}
return(0);
}
char *binbin(int n)
{
static char bin[17];
int x;
for(x=0;x<16;x++)
{
bin[x] = n & 0x8000 ? '1' : '0';
n <<= 1;
}
bin[x] = '\0';
return(bin);
}
Once upon a time, octal was popular
Another number format available in the C language is octal, or base 8. Octal was quite popular around the time Unix was developed, and many of the old, grizzled programmers league still enjoy tossing around octal values and doing octal-this or octal-that. C even sports an octal conversion character, %o.
I’ve not ever used octal in any of my programs. Some older code may use it, and occasionally some function references octal values. So my advice is to be aware of octal, but don’t bother to memorize anything.
The code in Listing 17-6 displays a value in binary, hexadecimal, and decimal and then shifts that value to the left, displaying the new value. This process takes place at Line 13 by using the %X conversion character in the printf() statement.
Well, actually, the placeholder is %04X, which displays hex values using uppercase letters, four digits wide, and padded with zeros on the left as needed. The 0x prefix before the conversion character merely displays the output in standard C style.
Exercise 17-13: Start a new project using the code from Listing 17-6. Build and run.
Exercise 17-14: Change the value of variable b in Line 9 to read this way:
b = 0x11;
Save that change, and build and run.
You can write hex values directly in your code. Prefix the values with 0x, followed by a valid hexadecimal number using either upper- or lowercase letters where required.