Logical Fallacies
Illusory Correlation
The brain is a giant pattern detector, and it seeks to extract order and structure from what often appear to be random configurations. We see Orion the Hunter in the night sky not because the stars were organized that way but because our brains can project patterns onto randomness.
When that friend phones you just as you’re thinking of them, that kind of coincidence is so surprising that your brain registers it. What it doesn’t do such a good job of is registering all the times you didn’t think of someone and they called you. You can think of this like one of those fourfold tables from Part One. Suppose it’s a particularly amazing week filled with coincidences (a black cat crosses your path as you walk by a junkyard full of broken mirrors, make your way up to the thirteenth floor of a building to find the movie Friday the 13th playing on a television set there). Let’s say you get twenty phone calls that week and two of them were from long-lost friends whom you hadn’t thought about for a while, but they called within ten minutes of you thinking of them. That’s the top row of your table: twenty calls, two that you summoned using extrasensory signaling, eighteen that you didn’t. But wait! We have to fill in the bottom row of the table: How many times were you thinking about people and they didn’t call, and—here’s my favorite—how many times were you not thinking about someone and they didn’t call?
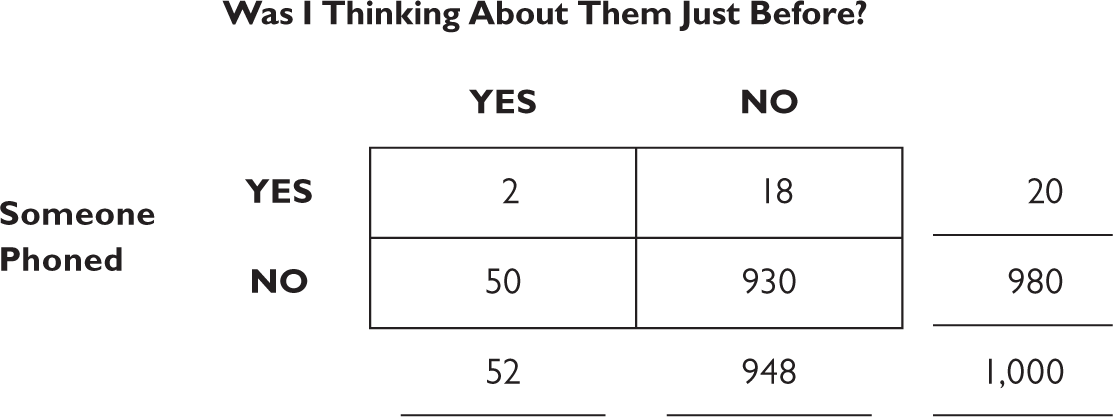
To fill out the rest of the table, let’s say there are 52 times in a week that you’re thinking about people, and 930 times in a week when you are not thinking about people. (This last one is just a crazy guess, but if we divide up the 168-hour week into ten-minute increments, that’s about 980 total thoughts, and we already know that 50 of those were about people who didn’t phone you, leaving 930 thoughts about things other than people; this is probably an underestimate, but the point is made with any reasonable number you care to put here—try it yourself.)
The brain really only notices the upper left-hand square and ignores the other three, much to the detriment of logical thinking (and to the encouragement of magical thinking). Now, before you book a trip to Vegas to play the roulette wheel, let’s run the numbers. What is the probability that someone will call given that you just thought about them? It’s only two out of fifty-two, or 4 percent. That’s right, 4 percent of the time when you think of someone they call you. That’s not so impressive.
What might account for the 4 percent of the times when this coincidence occurs? A physicist might just invoke the 1,000 events in your fourfold table and note that only two of them (two-tenths of 1 percent) appear to be “weird” and so you should just expect this by chance. A social psychologist might wonder if there was some external event that caused both you and your friend to think of each other, thus prompting the call. You read about the terrorist attacks in Paris on November 13, 2015. Somewhere in the back of your mind, you remember that you and a college friend always talked about going to Paris. She calls you and you’re so surprised to hear from her you forget the Paris connection, but she is reacting to the same event, and that’s why she picked up the phone.
If this reminds you of the twins-reared-apart story earlier, it should. Illusory correlation is the standard explanation offered by behavioral geneticists for the strange confluence of behaviors, such as both twins scratching their heads with their middle finger, or both wrapping tape around pens and pencils to improve their grip. We are fascinated by the contents of the upper left-hand cell in the fourfold table, fixated on all the things that the twins do in common. We tend to ignore all the things that one twin does and the other doesn’t.
Framing of Probabilities
After that phone call from your old college friend, you decide to go to Paris on vacation for a week next summer. While standing in front of the Mona Lisa, you hear a familiar voice and look up to see your old college roommate Justin, whom you haven’t seen in years. “I can’t believe it!” Justin says. “I know!” you say. “What are the odds that I’d run into you here in Paris, standing right in front of the Mona Lisa! They must be millions to one!”
Yes, the odds of running into Justin in front of the Mona Lisa are probably millions to one (they’d be difficult to calculate precisely, yet any calculation you do would make clear that this was very unlikely). But this way of framing the probability is fallacious. Let’s take a step back. What if you hadn’t run into Justin just as you were standing in front of the Mona Lisa, but as you were in front of the Venus de Milo, in les toilettes, or even as you were walking in the entrance? What if you had run into Justin at your hotel, at a café, or the Eiffel Tower? You would have been just as surprised. For that matter, forget about Justin—if you had run into anyone you knew during that vacation, anywhere in Paris, you’d be just as surprised. And why limit it to your vacation in Paris? It could be on a business trip to Madrid, while changing planes in Cleveland, or at a spa in Tucson. Let’s frame the probability this way: Sometime in your adult life, you’ll run into someone you know where you wouldn’t expect to run into them. Clearly the odds of that happening are quite good. But the brain doesn’t automatically think this way—cognitive science has shown us just how necessary it is for us to train ourselves to avoid squishy thinking.
Framing Risk
A related problem in framing probabilities is the failure to frame risks logically. Even counting the airplane fatalities of the 9/11 attacks in the United States, air travel remained (and continues to remain) the safest transportation mode, followed closely by rail transportation. The chances of dying on a commercial flight or train trip are next to zero. Yet, right after 9/11, many U.S. travelers avoided airplanes and took to the highways instead. Automobile deaths increased dramatically. People followed their emotional intuition rather than a logical response, oblivious to the increased risk. The rate of vehicular accidents did not increase beyond baseline, but the sum of people who died in all transportation-related accidents increased as more people chose a less safe mode of travel.
You might pull up a statistic such as this one:
More people died in plane crashes in 2014 than in 1960.
From this, you might conclude that air travel has become much less safe. The statistic is correct, but it’s not the statistic that’s relevant. If you’re trying to figure out how safe air travel is, looking at the total number of deaths doesn’t tell you that. You need to look at the death rate—the deaths per miles flown, or deaths per flight, or something that equalizes the baseline. There were not nearly as many flights in 1960, but they were more dangerous.
By similar logic, you can say that more people are killed on highways between five and seven p.m. than between two and four a.m., so you should avoid driving between five and seven. But the simple fact is that many times more people are driving between five and seven—you need to look at the rate of death (per mile or per trip or per car), not the raw number. If you do, you’ll find that driving in the evening is safer (in part because people on the road between two and four a.m. are more likely to be drunk or sleep-deprived).
After the Paris attacks of November 13, 2015, CNN reported that at least one of the attackers had entered the European Union as a refugee, against a backdrop of growing anti-refugee sentiment in Europe. Anti-refugee activists had been calling for stricter border control. This is a social and political issue and it is not my intention to take a stand on it, but the numbers can inform the decision making. Closing the borders completely to migrants and refugees might have thwarted the attacks, which took roughly 130 lives. Denying entry to a million migrants coming from war-torn regions such as Syria and Afghanistan would, with great certainty, have cost thousands of them their lives, far more than the 130 who died in the attacks. There are other risks to both courses of action, and other considerations. But to someone who isn’t thinking through the logic of the numbers, a headline like “One of the attackers was a refugee” inflames the emotions around anti-immigrant sentiment, without acknowledging the many lives that immigration policies saved. The lie that terrorists want you to believe is that you are in immediate and great peril.
Misframing is often used by salespeople to persuade you to buy their products. Suppose you get an email from a home-security company with this pitch: “Ninety percent of home robberies are solved with video provided by the homeowner.” It sounds so empirical. So scientific.
Start with a plausibility check. Forget about the second part of the sentence, about the video, and just look at the first part: “Ninety percent of home robberies are solved …” Does that seem reasonable? Without looking up the actual statistics, just using your real-world knowledge, it seems doubtful that 90 percent of home robberies are solved. This would be a fantastic success rate for any police department. Off to the Internet. An FBI page reports that about 30 percent of robbery cases are “cleared,” meaning solved.
So we can reject as highly unlikely the initial statement. It said 90 percent of home robberies are solved with video provided by the homeowner. But that can’t be true—it would imply that more than 90 percent of home robberies are solved, because some are certainly solved without home video. What the company more likely means is that 90 percent of solved robberies are from video provided by the homeowner.
Isn’t that the same thing?
No, because the sample pool is different. In the first case, we’re looking at all home robberies committed. In the second case we’re looking only at the ones that were solved, a much smaller number. Here it is visually:
All home robberies in a neighborhood:

Solved home robberies in a neighborhood (using the 30 percent figure obtained earlier):

So does that mean that if I have a video camera there is a 90 percent chance that the police will be able to solve a burglary at my house?
No!
All you know is that if a robbery is solved, there is a 90 percent chance that the police were aided by a home video. If you’re thinking that we have enough information to answer the question you’re really interested in (what is the chance that the police will be able to solve a burglary at my house if I buy a home-security system versus if I don’t), you’re wrong—we need to set up a fourfold table like the ones in Part One, but if you start, you’ll see that we have information on only one of the rows. We know which percentage of solved crimes had home video. But to fill out the fourfold table, we’d also need to know what proportion of the unsolved crimes had home video (or, alternatively, what proportion of the home videos taken resulted in unsolved crimes).
Remember, P(burglary solved | home video) ≠ P(home video | burglary solved).
The misframing of the data is meant to spark your emotions and cause you to purchase a product that may not have the intended result at all.
Belief Perseverance
An odd feature of human cognition is that once we form a belief or accept a claim, it’s very hard for us to let go, even in the face of overwhelming evidence and scientific proof to the contrary. Research reports say we should eat a low-fat, high-carb diet and so we do. New research undermines the earlier finding—quite convincingly—yet we are reluctant to change our eating habits. Why? Because on acquiring the new information, we tend to build up internal stories to help us assimilate the knowledge. “Eating fats will make me fat,” we tell ourselves, “so the low-fat diet makes a lot of sense.” We read about a man convicted of a grisly homicide. We see his picture in the newspaper and think that we can make out the beady eyes and unforgiving jaw of a cold-blooded murderer. We convince ourselves that he “looks like a killer.” His eyebrows arched, his mouth relaxed, he seems to lack remorse. When he’s later acquitted based on exculpatory evidence, we can’t shake the feeling that even if he didn’t do this murder, he must have done another one. Otherwise he wouldn’t look so guilty.
In a famous psychology experiment, participants were shown photos of members of the opposite sex while ostensibly connected to physiological monitoring equipment indicating their arousal levels. In fact, they weren’t connected to the equipment at all—it was under the experimenter’s control. The experimenter gave the participants false feedback to make them believe that they were particularly attracted to a person in one of the photos more than the others. When the experiment was over, the participants were shown that the “reactions” of their own body were in fact premanufactured tape recordings. The kicker is that the experimenter allowed them to choose one photo to take home with them. Logically, they should have chosen the picture that they found most attractive at that moment—the evidence for liking a particular picture had been completely discredited. But the participants tended to choose the picture that was consistent with their initial belief. The experimenters showed that the effect was driven by the sort of self-persuasion described above.
Autism and Vaccines: Four Pitfalls in Reasoning
The story with autism and vaccines involves four different pitfalls in critical thinking: illusory correlation, belief perseverance, persuasion by association, and the logical fallacy we saw earlier, post hoc, ergo propter hoc (loosely translated, it means “because this happened after that, that must have caused this”).
Between 1990 and 2010, the number of children diagnosed with autism spectrum disorders (ASD) rose sixfold, more than doubling in the last ten years. The prevalence of autism has increased exponentially from the 1970s to now.
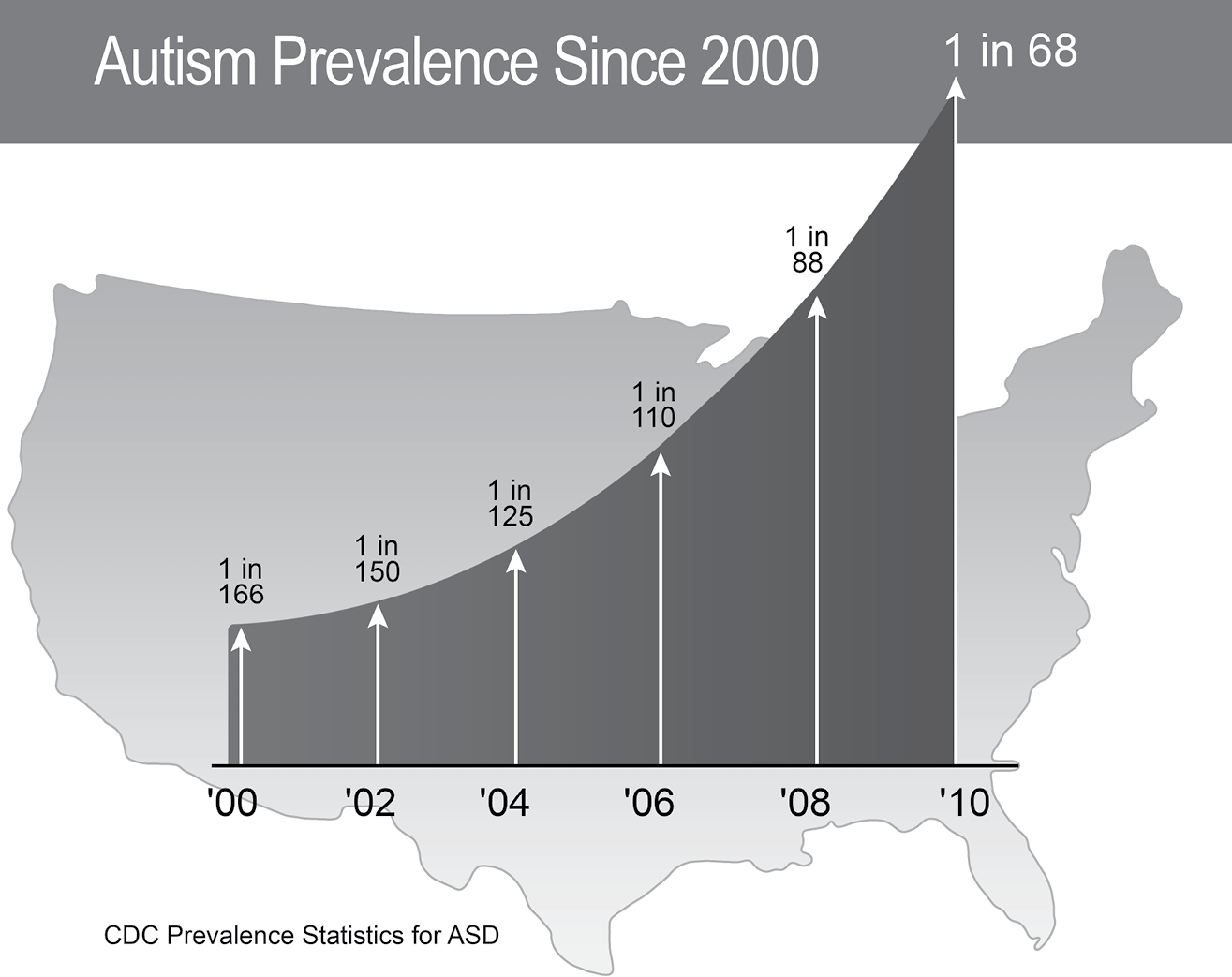
The majority of the rise has been accounted for by three factors: increased awareness of autism (more parents are on the alert and bring their children in for evaluation, professionals are more willing to make the diagnosis); widened definitions that include more cases; and the fact that people are having children later in life (advanced parental age is correlated with the likelihood of having children with autism and many other disorders).
If you allow the Internet to guide your thinking on why autism has increased, you’ll be introduced to a world of fiendish culprits: GMOs, refined sugar, childhood vaccines, glyphosates, Wi-Fi, and proximity to freeways. What’s a concerned citizen to do? It sure would be nice if an expert would weigh in. Voilà—an MIT scientist comes to the rescue! Dr. Stephanie Seneff made headlines in 2015 when she reported a link between a rise in the use of glyphosate, the active ingredient in the weed killer Roundup, and the rise of autism. That’s right, two things rise—like pirates and global warming—so there must be a causal connection, right?
Post hoc, ergo propter hoc, anyone?
Dr. Seneff is a computer scientist with no training in agriculture, genetics, or epidemiology. But she is a scientist at the venerable MIT, so many people wrongly assume that her expertise extends beyond her training. She also couches her argument in the language of science, giving it a real pseudoscientific, counterknowledge gloss:
- Glyphosate interrupts the shikimate pathway in plants.
- The shikimate pathway allows plants to create amino acids.
- When the pathway is interrupted, the plants die.
Seneff concedes that human cells don’t have a shikimate pathway, but she continues:
- We have millions of bacteria in our gut (“gut flora”).
- Those bacteria do have a shikimate pathway.
- When glyphosate enters our system, it disturbs our digestion and our immune function.
- Glyphosate in humans can also inhibit liver function.
If you’re wondering what all this has to do with ASD, you should be. Seneff lays out a case (without citing any evidence) for increased prevalence of digestive problems and immune system dysfunction, but these have nothing to do with ASD.
Others searching for an explanation for the rise in autism rates have pointed to the MMR (measles-mumps-rubella) vaccine, and the antiseptic, antifungal compound thimerosal (thiomersal) it contains. Thimerosal is derived from mercury, and the amount contained in vaccines is typically one-fortieth of what the World Health Organization (WHO) considers the amount tolerable per day. Note that the WHO guidelines are expressed as per-day amounts, and with the vaccine, you’re getting it only once.
Although there was no evidence that thimerosal was linked to autism, it was removed from vaccines in 1992 in Denmark and Sweden, and in the United States starting in 1999, as a “precautionary measure.” Autism rates have continued to increase apace even with the agent removed. The illusory correlation (as in pirates and global warming) is that the MMR vaccine is typically given between twelve and fifteen months of age, and if a child has autism, the earliest that it is typically diagnosed is between eighteen and twenty-four months of age. Parents tended to focus on the upper left-hand cell of a fourfold table—the number of times a child received a vaccination and was later diagnosed with autism—without considering how many children who were not vaccinated still developed autism, or how many millions of children were vaccinated and did not develop autism.
To make matters worse, a now-discredited physician, Andrew Wakefield, published a scientific paper in 1998 claiming a link. The British Medical Journal declared his work fraudulent, and six years later, the journal that originally published it, the Lancet, retracted it. His medical license was revoked. Wakefield was a surgeon, not an expert in epidemiology, toxicology, genetics, neurology, or any specialization that would have qualified him as an expert on autism.
Post hoc, ergo propter hoc caused people to believe the correlation implied causation. Illusory correlation caused them to focus only on the coincidence of some people developing autism who also had the vaccine. The testimony of a computer scientist and a physician caused people to be persuaded by association. Belief perseverance caused people who initially believed the link to cling to their beliefs even after the evidence had been removed.
Parents continue to blame the vaccine for autism, and many parents stopped vaccinating their children. This led to several outbreaks of measles around the world. All because of a spurious link and the failure of a great many people to distinguish between correlation and causation, and a failure to form beliefs based on what is now overwhelming scientific evidence.