In our lives, people face all kinds of choices. In a sense, we implement, either consciously or subconsciously, various kinds of implied optimization procedures. For example, when a high school junior or senior is looking for a college, they might have many choices, such as good schools, local schools, public schools, or private schools. When making a decision with a couple of offers, these high school students usually have some objectives in their mind. These objectives might include the ranking and cost of attending a school, scholarships, the reputation, and name recognition of the program, or even the fame of the football team. For corporations, they have to make all kinds of optimal or reasonable decisions. For instance, what kinds of products they should produce, what are the quantities and at what prices, and to whom they should target. Since most companies have limited resources, they have to make an optimal decision with certain constraints. For example, in employee scheduling, the target function is the total cost. At the same time, we have certain constraints such as the number of employees, their seniority, preferences, and the like.
Here is a general form for the optimization problem, where Min() is a minimizing function and f(x) is our objective function:
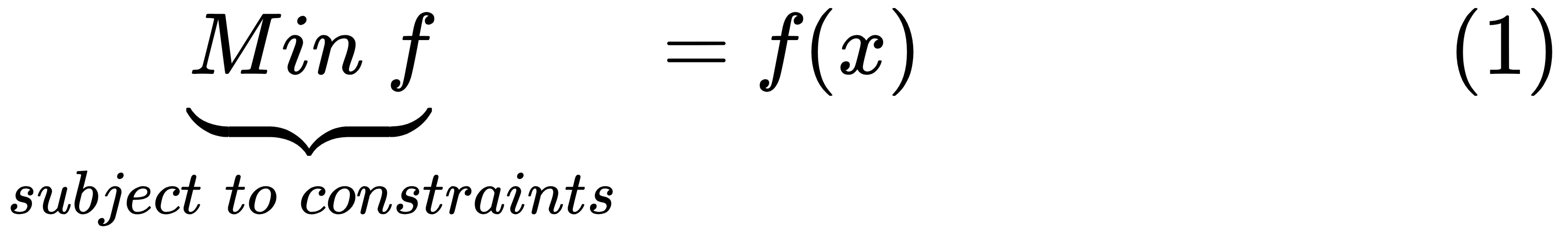
We intend to minimize f by changing x, which is a set of input values, by subjecting it to certain constraints. Note that if we plan to maximize f, we simply could have minimized its negative value. Later in the chapter, we introduce a utility function for investors, which could be viewed as the trade-off between benefits (expected portfolio return) and cost (the portfolio risk). For investors, they want to maximize the utility. It could be equivalent to minimizing its negative objective function; see the following formula:

Where U() is the utility function and x will be a set of input variables. The following table shows a partial list of applications for optimization:
|
Area
|
Name
|
Description
|
|
Economics
|
Utility function | For many variables in the real world, it is difficult to quantify them, such as happiness. For this, economists have developed a utility function. To find an optimal solution, users could maximize their utility function. |
| Quantity, price, and production | A company might consider the best strategy to produce, price, and sell its products. | |
| Welfare transfer | Governments might consider many input variables such as incentives to work, crime rate, and other factors. | |
| Optimal tax policy | Maximize the GDP growth, subject to controllable inflation rate. | |
|
Finance
|
Portfolio optimization | For a given portfolio of expected returns, choose a set of stocks to minimize the portfolio risk. |
| Optimal investment strategy | When facing several possible investment opportunities and many constraints, how to choose the best combination to achieve the best result. | |
| Profit optimization | For companies, they want to maximize their profit by optimally choosing their input variables. | |
| High-frequency trading | Balance the signalling effect with various bid-and-ask offers, and long-term and short-term profits. | |
|
Others
|
Scheduling | Minimize the total cost with certain constraints. |
| Minimize total cost | Consider various trade-offs between certain benefits and costs. | |
| Flying issues | Minimize the total distance by visiting certain cities. | |
| Task arrangements | With many tasks and potential labor and input variables available, how to achieve an optimal solution. |