For predicting a future possible event, one of the tools is the Monte Carlo simulation. For this purpose, we could use a Julia package called QuantEcon. This package is Quantitative Economics with Julia. The first example is the Markov simulation:
using QuantEcon
P = [0.4 0.6; 0.2 0.8];
mc = MarkovChain(P)
x = simulate(mc, 100000);
mean(x .== 1)
#
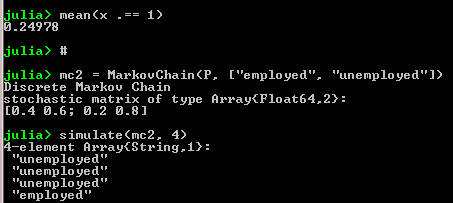
mc2 = MarkovChain(P, ["employed", "unemployed"])
simulate(mc2, 4)
The first part of the program simulates 100,000 times of P matrix while the second part simulates two statuses: employed and unemployed. See the following output:
The next example is also borrowed from the manual. The objective is to see how a person from one economic status transforms to another one in the future. First, let's see the following graph:

Let's look at the leftmost oval with poor inside. It means for a poor person he/she has 90% chance to remain poor and 10% moves to the middle class. It could be represented by the following matrix, putting zeros where there's no edge between nodes:
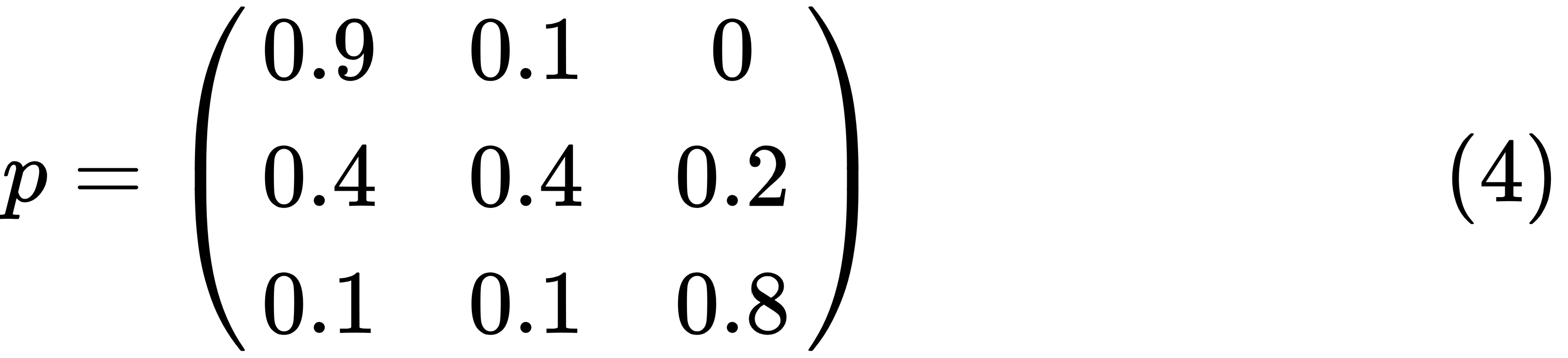
Two states, x and y, are said to communicate with each other if there exists positive integers j and k, such as:

The stochastic matrix P is called irreducible if all states communicate; that is, if x and y communicate for every (x, y). It's clear from the graph that this stochastic matrix is irreducible: we can reach any state from any other state eventually. The following code would confirm this:
using QuantEcon
P = [0.9 0.1 0.0; 0.4 0.4 0.2; 0.1 0.1 0.8];
mc = MarkovChain(P)
is_irreducible(mc)
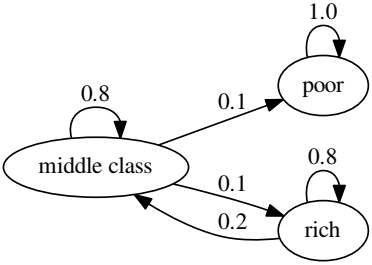
The following graph would represent an extreme case for irreducible since the future status for a poor person will be 100% poor:
The following code would confirm this as well, as the result will be false:
using QuantEcon
P2 = [1.0 0.0 0.0; 0.1 0.8 0.1; 0.0 0.2 0.8];
mc2 = MarkovChain(P2)
is_irreducible(mc2)