As we mentioned at the beginning of the chapter, we could show several applications of multivariable linear models. The first one is a three-factor linear model. The general formula is quite similar to the one-factor linear model, shown here:
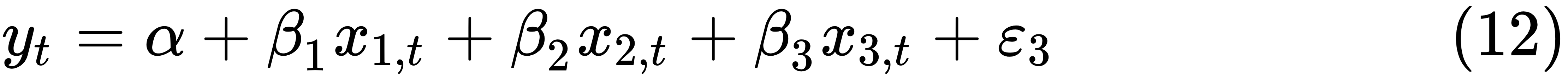
The definitions are the same as before. The only difference is that we have three independent variables instead of one. Our objective is to estimate four parameters, one intercept plus three coefficients:
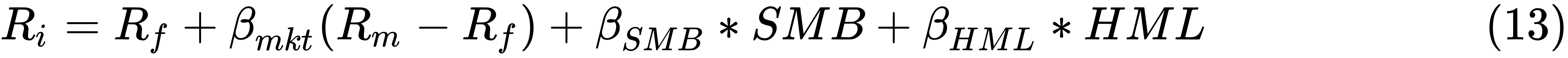
For example, the equation of the famous Fama-French 3-factor model is given, where Ri is the stock i's return and Rm is the market return. SMB (Small Minus Big) is defined as the returns of the small portfolios minus the returns of the big portfolios and HML (High Minus Low) is the difference of returns of high book-to-market portfolios minus the returns of low book-to-market portfolios. (See the Ken French data library at http://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html for more detailed definitions.) To download these three factors, we could go to Prof. French's data library to download them, as shown in the following steps:
- Go to the previous link.
- Choose CSV for the monthly data (the first line in the following screenshot):

The first several lines of the unzipped csv file are shown here:
This file was created by CMPT_ME_BEME_RETS using the 201712 CRSP database.
The 1-month TBill return is from Ibbotson and Associates, Inc.
,Mkt-RF,SMB,HML,RF
192607, 2.96, -2.30, -2.87, 0.22
192608, 2.64, -1.40, 4.19, 0.25
192609, 0.36, -1.32, 0.01, 0.23
192610, -3.24, 0.04, 0.51, 0.32
192611, 2.53, -0.20, -0.35, 0.31
192612, 2.62, -0.04, -0.02, 0.28
192701, -0.06, -0.56, 4.83, 0.25
192702, 4.18, -0.10, 3.17, 0.26
192703, 0.13, -1.60, -2.67, 0.30
192704, 0.46, 0.43, 0.60, 0.25
This file was created by CMPT_ME_BEME_RETS using the 201712 CRSP database:
The 1-month TBill return is from Ibbotson and Associates, Inc.
,Mkt-RF,SMB,HML,RF
192607, 2.96, -2.30, -2.87, 0.22
192608, 2.64, -1.40, 4.19, 0.25
192609, 0.36, -1.32, 0.01, 0.23
192610, -3.24, 0.04, 0.51, 0.32
192611, 2.53, -0.20, -0.35, 0.31
192612, 2.62, -0.04, -0.02, 0.28
192701, -0.06, -0.56, 4.83, 0.25
192702, 4.18, -0.10, 3.17, 0.26
192703, 0.13, -1.60, -2.67, 0.30
192704, 0.46, 0.43, 0.60, 0.25
In R, we could issue the following code to download it from the author's website:
> con<-url("http://canisius.edu/~yany/RData/ff3monthly.RData")
> load(con)
> head(.ff3monthly)
DATE MKT_RF SMB HML RF
1 1926-07-01 0.0296 -0.0230 -0.0287 0.0022
2 1926-08-01 0.0264 -0.0140 0.0419 0.0025
3 1926-09-01 0.0036 -0.0132 0.0001 0.0023
4 1926-10-01 -0.0324 0.0004 0.0051 0.0032
5 1926-11-01 0.0253 -0.0020 -0.0035 0.0031
6 1926-12-01 0.0262 -0.0004 -0.0002 0.0028
For the following R program, we can run the Fama-French 3-factor model for IBM:
con<-url("http://canisius.edu/~yany/RData/ff3monthly.RData")
load(con)
head(.ff3monthly)
x<-read.csv("http://canisius.edu/~yany/data/ibmMonthly.csv")
stock<-ret_f(x)
final<-merge(stock,.ff3monthly)
y<-final$RET
x<-as.matrix(data.frame(final[,3:5]))
summary(lm(y~x))
In the previous code, we assume that the function called ret_f() is available (see the previous discussion about this function). The output is shown here:

Here is the Fama-French-Carhart's 4-factor model:
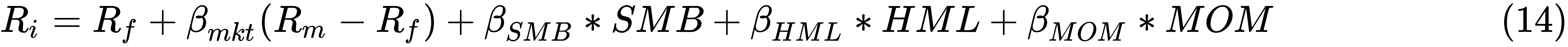
To download these four factors (Market, SMB, HML, and Momentum), we go to Professor Ken French's data library to download two zipped files:
con<-url("http://canisius.edu/~yany/RData/ffc4monthly.RData")
load(con)
head(.ffc4monthly)
The related output is shown here:
DATE MKT_RF SMB HML MOM RF 1 1927-01-31 -0.0006 -0.0056 0.0483 0.0044 0.0025 2 1927-02-28 0.0418 -0.0010 0.0317 -0.0201 0.0026 3 1927-03-31 0.0013 -0.0160 -0.0267 0.0359 0.0030 4 1927-04-30 0.0046 0.0043 0.0060 0.0419 0.0025 5 1927-05-31 0.0544 0.0141 0.0493 0.0301 0.0030 6 1927-06-30 -0.0234 0.0047 -0.0153 0.0051 0.0026
To save space, we would not run a Fama-French-Carhart 4-factor model since it is quite similar to running the CAPM and Fama-French 3-factor model.
In 2014, Fama and French developed their 5-factor model, which has the following form:
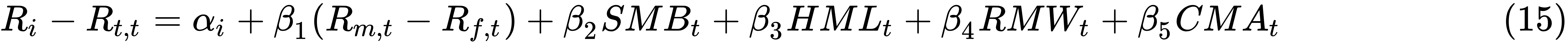
In the equation, RMWt is the return difference between portfolios of stocks with robust and weak profitability, and CMAt is the return difference between portfolios of low and high investment stocks. Fama and French call the low and high investment stocks conservative and aggressive, respectively. If the sensitivities to the five factors, βi (i=1,2,...,5), capture all the variations in the expected returns, the intercept αi will be zero for all securities and portfolios i. The following R program downloads the ff5Monthly.RData set from the author's website:
> con<-url("http://canisius.edu/~yany/RData/ff5Monthly.RData")
> load(con)
> head(.ff5Monthly)
The related output is shown here:
DATE MKT_RF SMB HML RMW CMA RF
1 1963-07-01 -0.0039 -0.0046 -0.0082 0.0072 -0.0116 0.0027
2 1963-08-01 0.0507 -0.0081 0.0163 0.0042 -0.0040 0.0025
3 1963-09-01 -0.0157 -0.0048 0.0019 -0.0080 0.0023 0.0027
4 1963-10-01 0.0253 -0.0129 -0.0011 0.0275 -0.0226 0.0029
5 1963-11-01 -0.0085 -0.0084 0.0166 -0.0034 0.0222 0.0027
6 1963-12-01 0.0183 -0.0187 -0.0011 0.0018 -0.0031 0.0029